Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Курс высшей математики
Содержание
- 1. Курс высшей математики
- 2. Лекция 92. Исследование формы поверхностейвторого порядка по их каноническимуравнениям1. Основные понятияПоверхности второго порядка
- 3. Определение.F(x, y,z) = 0,
- 4. Определение.Алгебраической поверхностью второго порядка называется поверхность ,
- 5. Всякое уравнение (2), задающее невырожденную поверхность, путем
- 6. Исследование формы поверхностей второгопорядка по их каноническим
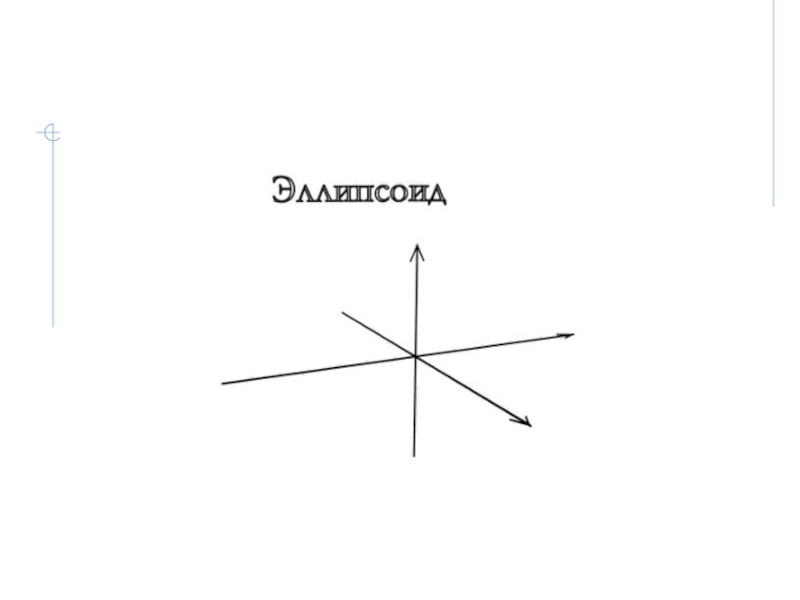
- 7. 2.1 ЭллипсоидЭллипсоидом называется поверхность второго порядка с каноническим уравнением
- 8. илиИССЛЕДОВАНИЕ ФОРМЫ ЭЛИПСОИДА МЕТОДОМ СЕЧЕНИЙГ-эллипс с полуосями a и b.
- 9. илиИССЛЕДОВАНИЕ ФОРМЫ ЭЛИПСОИДА МЕТОДОМ СЕЧЕНИЙГ-эллипс с полуосями и ,
- 10. ИССЛЕДОВАНИЕ ФОРМЫ ЭЛИПСОИДА МЕТОДОМ СЕЧЕНИЙ
- 11. Аналогично рассматриваются сечения поверхности плоскостями:Выполненное исследование завершается построением чертежа.
- 12. Слайд 12
- 13. При этом линиями пересечения эллипсоида с плоскостями
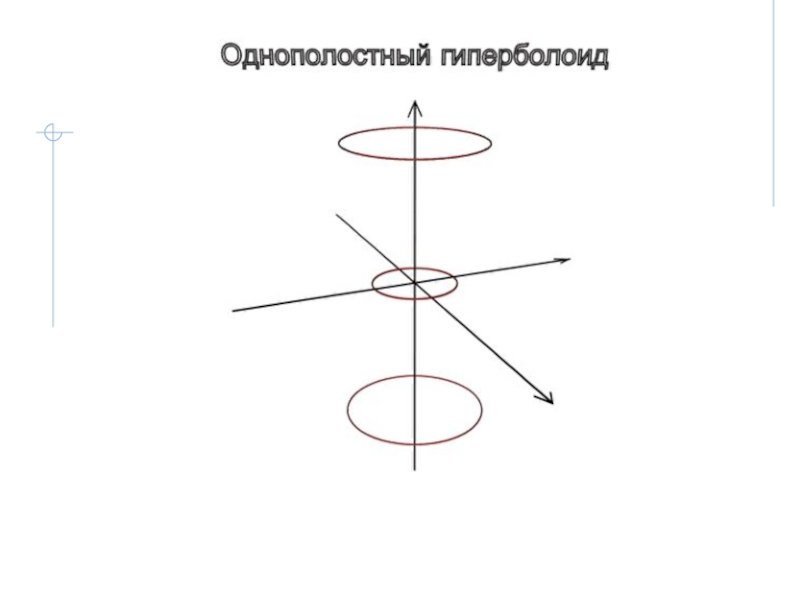
- 14. 2.2 Гиперболоиды 2.2.1 Однополостный гиперболоидОднополостным гиперболоидом называется поверхность второго порядка с каноническим уравнением:
- 15. определяющей эллипс с полуосями а и b. ИССЛЕДОВАНИЕ ФОРМЫ ОДНОПОЛОСТНОГО ГИПЕРБОЛОИДА МЕТОДОМ СЕЧЕНИЙ
- 16. В сечении плоскостью
- 17. задают гиперболу, пересекающую ось OY. Уравнения линии пересечения:ИССЛЕДОВАНИЕ ФОРМЫ ОДНОПОЛОСТНОГО ГИПЕРБОЛОИДА МЕТОДОМ СЕЧЕНИЙ
- 18. ЗамечаниеСоответствующая поверхность является однополостным гиперболоидом вращения с осью OZ.Итоговый чертеж представлен на рисунке.
- 19. Слайд 19
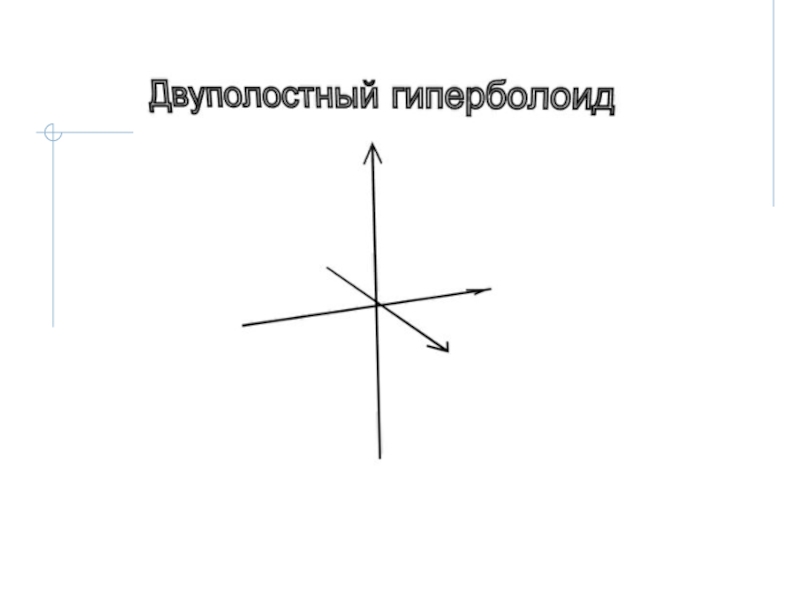
- 20. 2.2.2 Двуполостный гиперболоидДвуполостным гиперболоидом называется поверхность второго порядка с каноническим уравнением
- 21. где Если –с < h < c сечение – пустое множество.ИССЛЕДОВАНИЕ ФОРМЫ ДВУПОЛОСТНОГО ГИПЕРБОЛОИДА МЕТОДОМ СЕЧЕНИЙ
- 22. задает гиперболу, пересекающую ось OZ. Итоговый чертеж представлен на рисунке. ИССЛЕДОВАНИЕ ФОРМЫ ДВУПОЛОСТНОГО ГИПЕРБОЛОИДА МЕТОДОМ СЕЧЕНИЙ
- 23. Слайд 23
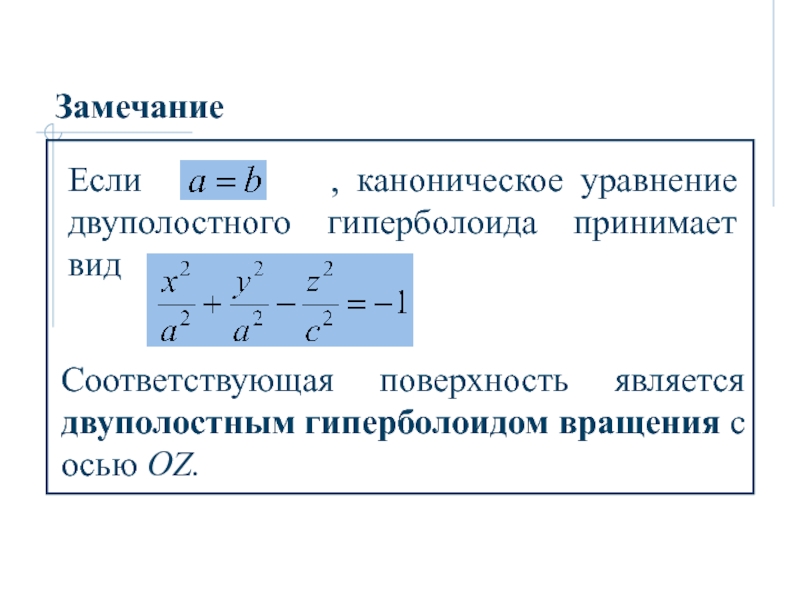
- 24. ЗамечаниеСоответствующая поверхность является двуполостным гиперболоидом вращения с осью OZ.
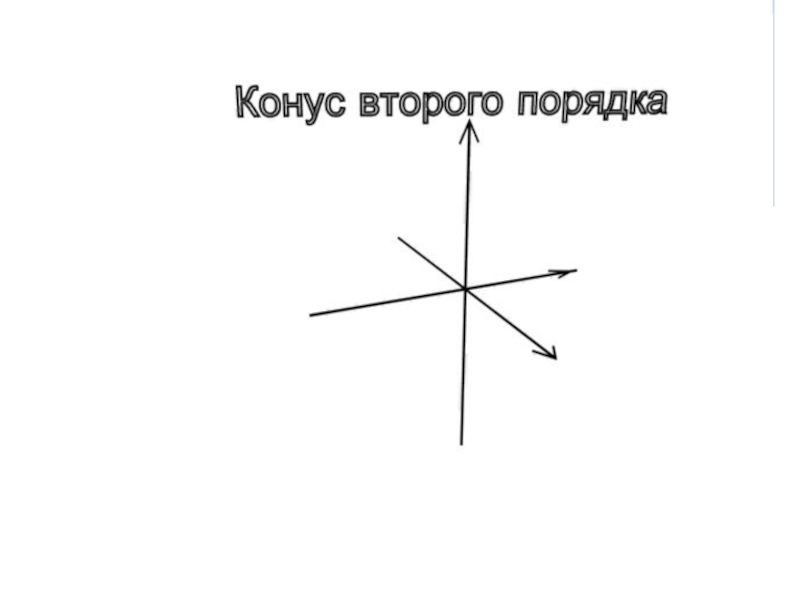
- 25. 2.3 КонусКонусом второго порядка называется поверхность с каноническим уравнением
- 26. Слайд 26
- 27. ЗамечаниеКонус является вырожденным гиперболоидом.Осью конуса, заданного рассматриваемым каноническим уравнением, является ось OZ.Поперечные сечения являются эллипсами.
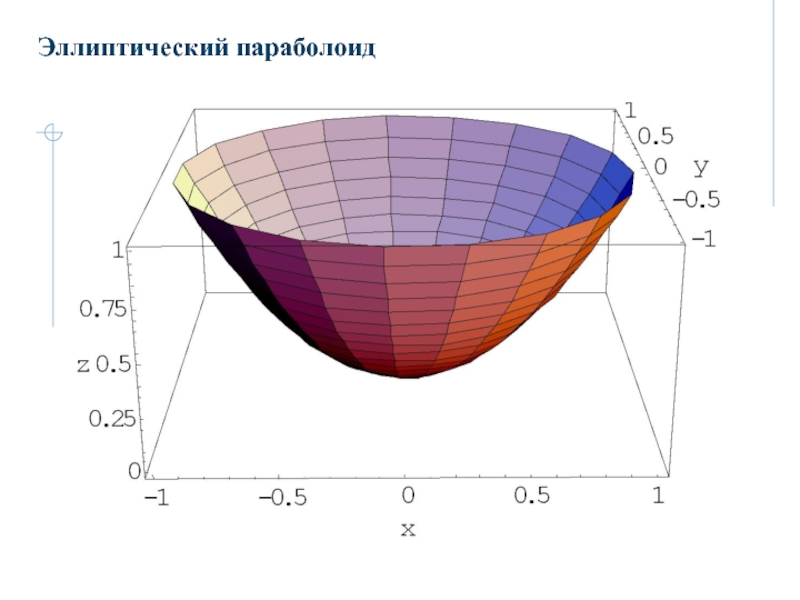
- 28. 2.4 Параболоиды 2.4.1 Эллиптический параболоидЭллиптическим параболоидом
- 29. Эллиптический параболоид
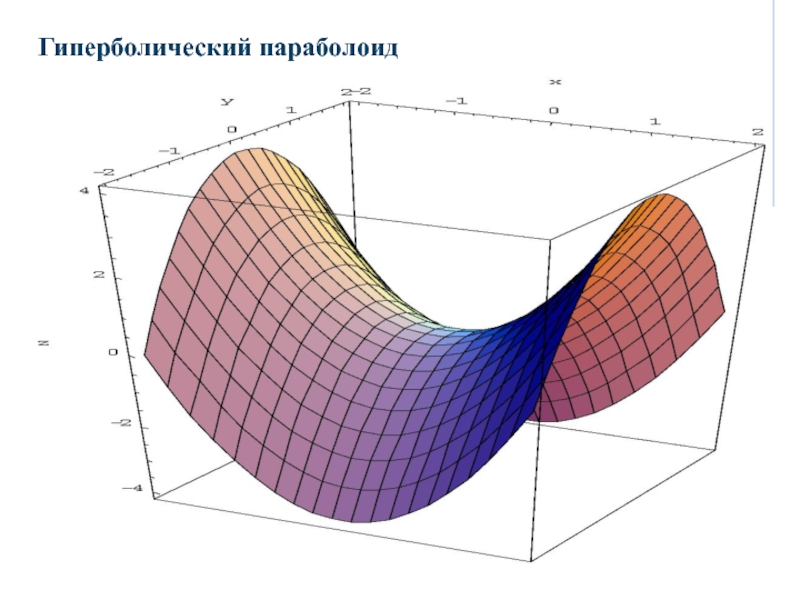
- 30. 2.4.2 Гиперболический параболоидГиперболическим параболоидом называется поверхность с каноническим уравнением
- 31. Отсюда и название исследуемой поверхности, форма которой представлена на рисунке. ИССЛЕДОВАНИЕ ФОРМЫ ГИПЕРБОЛИЧЕСКОГО ПАРАБОЛОИДА МЕТОДОМ СЕЧЕНИЙ
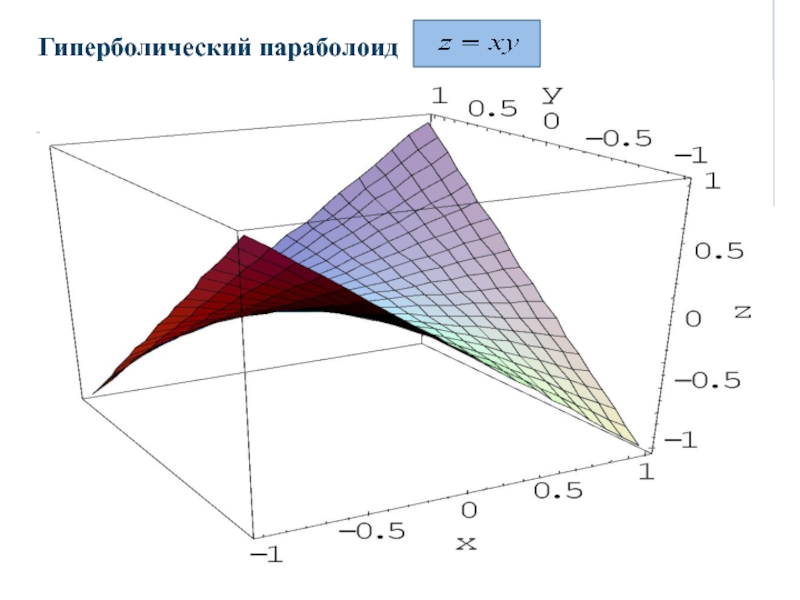
- 32. Гиперболический параболоид
- 33. Гиперболический параболоид
- 34. Гиперболический параболоид
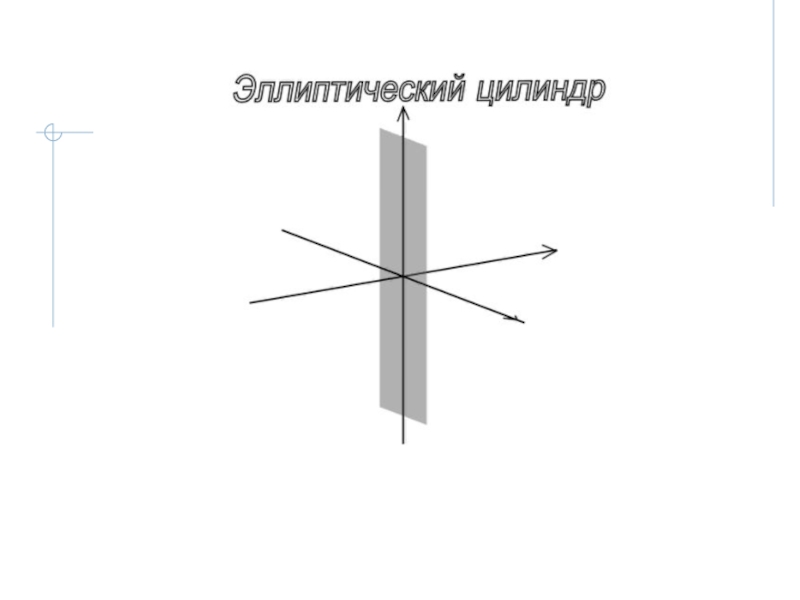
- 35. 2.5 Цилиндры второго порядка 2.5.1 Эллиптический
- 36. Слайд 36
- 37. 2.5.2 Гиперболический цилиндрГиперболический цилиндр задается каноническим уравнением Его форма представлена на рисунке.
- 38. Гиперболический цилиндр
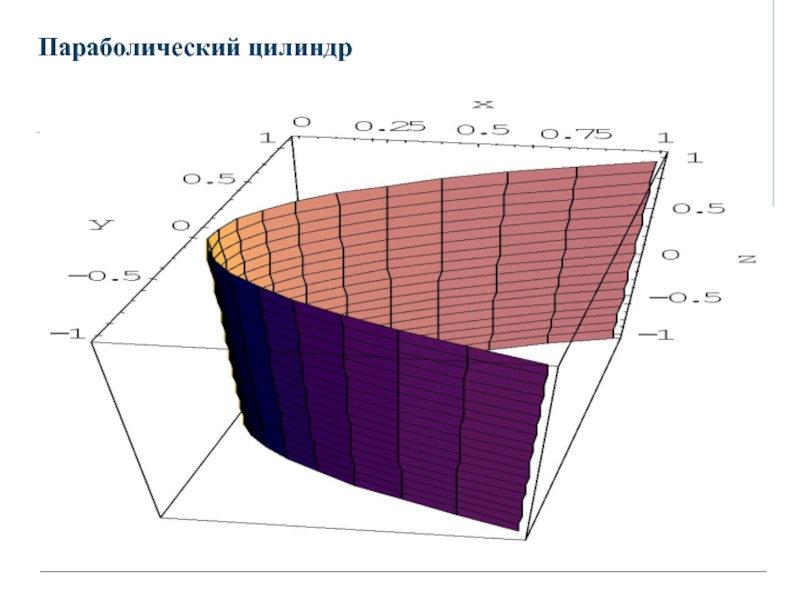
- 39. 2.5.2 Параболический цилиндрПараболический цилиндр задается каноническим уравнениемЕго форма представлена на рисунке.
- 40. Параболический цилиндр
- 41. ЗамечаниеПризнаком рассмотренных цилиндрических поверхностей является отсутствие одной из переменных в каноническом уравнении.
- 42. Скачать презентанцию
Лекция 92. Исследование формы поверхностейвторого порядка по их каноническимуравнениям1. Основные понятияПоверхности второго порядка
Слайды и текст этой презентации
Слайд 2Лекция 9
2. Исследование формы поверхностей
второго порядка по их каноническим
уравнениям
1. Основные
понятия
Слайд 3Определение.
F(x, y,z) = 0,
(1)
которому удовлетворяют координаты каждой точки, принадлежащей поверхности,
и не удовлетворяют координаты точки, не принадлежащей поверхности. Уравнением поверхности называется такое уравнение с тремя переменными
Слайд 4Определение.
Алгебраической поверхностью второго порядка называется поверхность , уравнение которой в
декартовой системе координат имеет вид
Ax2+By2+Cz2+2Dxy+2Exz+
+2Fyz+Gx+Hy+Iz+K=0, (2)
где не все
коэффициенты при членах второго порядка равны одновременно нулю.
Слайд 5Всякое уравнение (2), задающее невырожденную поверхность, путем преобразования координат можно
привести к каноническому виду, при котором каждая переменная содержится в
уравнении только в одной степени, либо только в первой, либо только во второй, а смешанные произведения отсутствуют.
Слайд 6Исследование формы поверхностей второго
порядка по их каноническим уравнениям
Основным методом исследования
формы поверхности по ее уравнению является метод сечений, когда о
форме поверхности судят по форме кривых, которые получаются при пересечении данной поверхности плоскостями:
Слайд 11Аналогично рассматриваются сечения поверхности плоскостями:
Выполненное исследование завершается построением чертежа.
Слайд 13При этом линиями пересечения эллипсоида с плоскостями z = h,
где –с < h < c , являются окружности, центры
которых лежат на оси OZ.Замечание
Следовательно, в этом случае эллипсоид является фигурой вращения с осью OZ.
Слайд 14 2.2 Гиперболоиды
2.2.1 Однополостный гиперболоид
Однополостным гиперболоидом называется поверхность второго
порядка с каноническим уравнением:
Слайд 15определяющей эллипс с полуосями а и b.
ИССЛЕДОВАНИЕ ФОРМЫ ОДНОПОЛОСТНОГО
ГИПЕРБОЛОИДА МЕТОДОМ СЕЧЕНИЙ
Слайд 16В сечении плоскостью имеем кривую
являющуюся
также эллипсом с полуосями
ИССЛЕДОВАНИЕ ФОРМЫ ОДНОПОЛОСТНОГО ГИПЕРБОЛОИДА МЕТОДОМ СЕЧЕНИЙ
Слайд 17задают гиперболу, пересекающую ось OY.
Уравнения линии пересечения:
ИССЛЕДОВАНИЕ ФОРМЫ ОДНОПОЛОСТНОГО
ГИПЕРБОЛОИДА МЕТОДОМ СЕЧЕНИЙ
Слайд 18Замечание
Соответствующая поверхность является однополостным гиперболоидом вращения с осью OZ.
Итоговый чертеж
представлен на рисунке.
Слайд 20 2.2.2 Двуполостный гиперболоид
Двуполостным гиперболоидом называется поверхность второго порядка с
каноническим уравнением
Слайд 21где
Если –с < h < c сечение – пустое
множество.
ИССЛЕДОВАНИЕ ФОРМЫ ДВУПОЛОСТНОГО ГИПЕРБОЛОИДА МЕТОДОМ СЕЧЕНИЙ
Слайд 22задает гиперболу, пересекающую ось OZ.
Итоговый чертеж представлен на рисунке.
ИССЛЕДОВАНИЕ ФОРМЫ ДВУПОЛОСТНОГО ГИПЕРБОЛОИДА МЕТОДОМ СЕЧЕНИЙ
Слайд 24Замечание
Соответствующая поверхность является двуполостным гиперболоидом вращения с осью OZ.
Слайд 27Замечание
Конус является вырожденным гиперболоидом.
Осью конуса, заданного рассматриваемым каноническим уравнением, является
ось OZ.
Поперечные сечения являются эллипсами.
Слайд 28 2.4 Параболоиды
2.4.1 Эллиптический параболоид
Эллиптическим параболоидом называется поверхность с
каноническим уравнением
Его форма проиллюстрирована на рисунке.
Слайд 30 2.4.2 Гиперболический параболоид
Гиперболическим параболоидом называется поверхность с каноническим уравнением
Слайд 31Отсюда и название исследуемой поверхности, форма которой представлена на рисунке.
ИССЛЕДОВАНИЕ ФОРМЫ ГИПЕРБОЛИЧЕСКОГО ПАРАБОЛОИДА МЕТОДОМ СЕЧЕНИЙ
Слайд 35 2.5 Цилиндры второго порядка
2.5.1 Эллиптический цилиндр
Эллиптический цилиндр
задается каноническим уравнением
Осью цилиндра является координатная ось OZ, поперечные
сечения – эллипсы. 
Слайд 37 2.5.2 Гиперболический цилиндр
Гиперболический цилиндр задается каноническим уравнением
Его форма
представлена на рисунке.
Слайд 39 2.5.2 Параболический цилиндр
Параболический цилиндр задается каноническим уравнением
Его форма представлена
на рисунке.
Слайд 41Замечание
Признаком рассмотренных цилиндрических поверхностей является отсутствие одной из переменных в
каноническом уравнении.
