Слайд 1Курсовая работа на тему:
Статистическая обработка результатов испытаний и проверка гипотез
о виде распределения
Работа выполнена студенткой II курса
экономического факультета,
специальности «бухгалтерский
учет,
анализ и аудит» Сапожниковой Е.Е.
Слайд 2Структура курсовой работы
Введение
1 часть:
1. Статистическая обработка результатов испытаний
1.1 Равномерный закон
распределения
1.2. Показательный (экспоненциальный) закон распределения
1.3. Нормальный закон распределения
1.4. –
распределение
1.5. Распределение Стьюдента
1.6. Распределение Фишера—Снедекора
2. Проверка гипотез о виде распределения
2 часть:
Практическое задание
Заключение
Список использованной литературы
Слайд 3Статистическая обработка результатов испытаний
Слайд 4Равномерный закон распределения
Непрерывная случайная величина X имеет равномерный закон распределения
на отрезке [а, b], если ее плотность вероятности (х)
постоянна на этом отрезке и равна нулю вне его
Слайд 5Использование равномерного закона распределения:
Равномерный закон распределения используется при анализе ошибок
округления при проведении числовых расчетов
Слайд 6Показательный (экспоненциальный) закон распределения
Непрерывная случайная величина X имеет показательный
(экспоненциальный) закон распределения с параметром > 0, если ее
плотность вероятности имеет вид
Слайд 7Использование показательного закона распределения:
Показательный закон распределения играет большую роль в
теории массового обслуживания и теории надежности. Так, например, интервал времени
Т между двумя соседними событиями в простейшем потоке имеет показательное распределение с параметром — интенсивностью потока.
Слайд 8Пример задачи по показательному закону распределения
Дано: Доказать, что если промежуток
времени Т, распределенный по показательному закону, уже длился некоторое время
, то это никак не влияет на закон распределения оставшейся части
T1=T- промежутка, т.е. закон распределения T1 остается таким же, как и всего промежутка Т.
Решение: Вероятность события:
Ответ:
Слайд 9Нормальный закон распределения
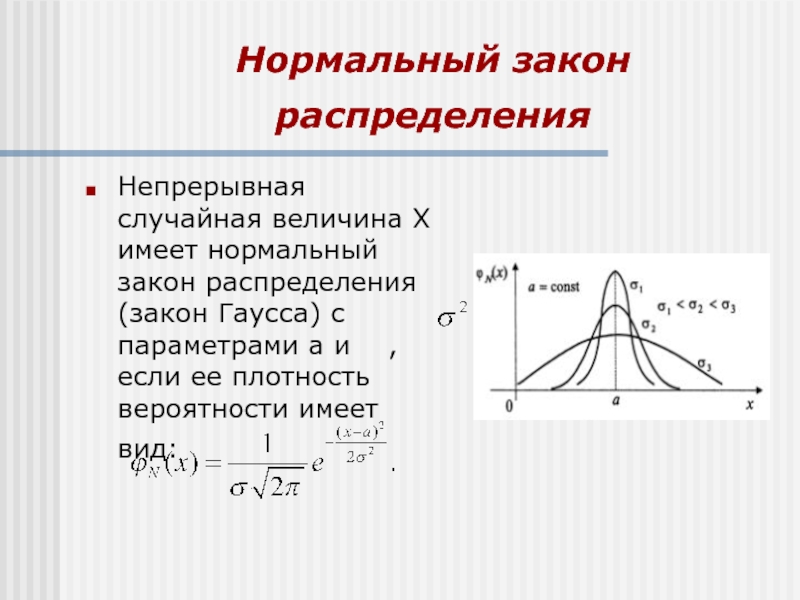
Непрерывная случайная величина X имеет нормальный закон
распределения (закон Гаусса) с параметрами а и , если
ее плотность вероятности имеет вид:
Слайд 10Использование нормального закона распределения:
Многие признаки подчиняются нормальному закону, например, рост
человека, дальность полета снаряда и т.п. Но если какой-либо признак
подчиняется другому, отличному от нормального, закону распределения, то это вовсе не говорит о «ненормальности» явления, связанного с этим признаком.
Слайд 11Пример задачи по нормальному закону
Дано: Полагая, что рост мужчин определенной
возрастной группы есть нормально распределенная случайная величинах Х с параметрами
а = 173 и = 36, найти:
1. а) выражение плотности вероятности и функции распределения случайной величины X;
б) доли костюмов 4-го роста (176— 182 см) и 3-го роста (170—176 см), которые нужно предусмотреть в общем объеме производства для данной возрастной группы;
в) квантиль и 10%-ную точку случайной величины X .
2. Сформулировать «правило трех сигм» для случайной величины X.
Решение:Найдем квантиль случайной величины X:
откуда
Это означает, что 70% мужчин данной возрастной группы имеют рост до 176 см. 10%-ная точка — это квантиль = 181 см (находится аналогично), т.е. 10% мужчин имеют рост не менее 181 см.
Находим t cм
Слайд 12 - распределение
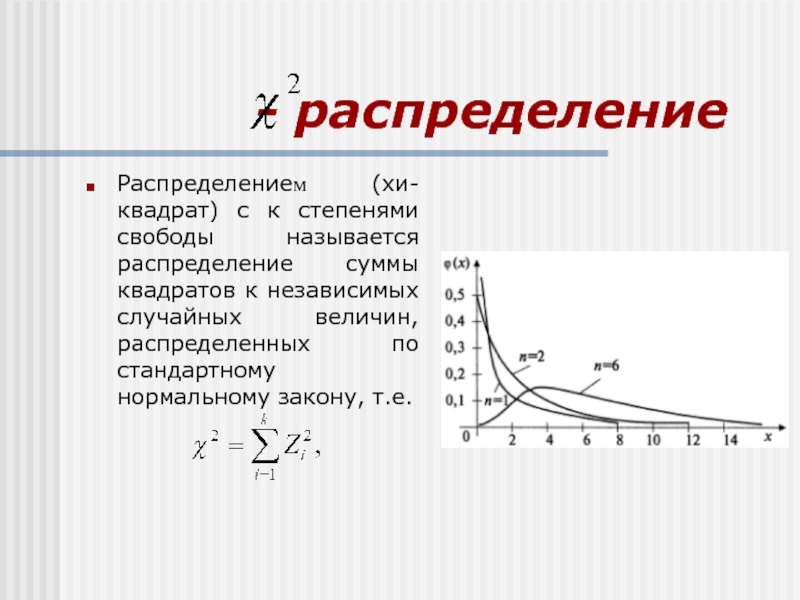
Распределением (хи-квадрат) с к
степенями свободы называется распределение суммы квадратов к независимых случайных величин,
распределенных по стандартному нормальному закону, т.е.
Слайд 13Распределение Стьюдента
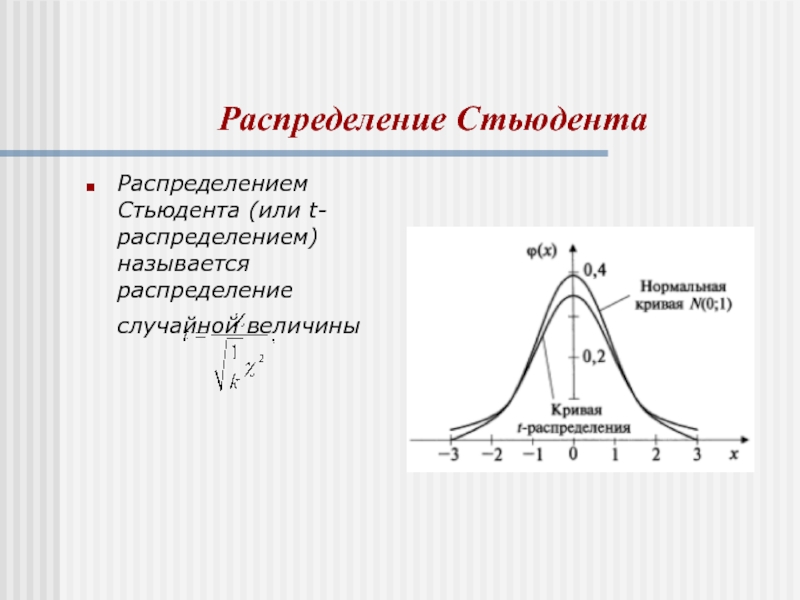
Распределением Стьюдента (или t-распределением) называется распределение случайной величины
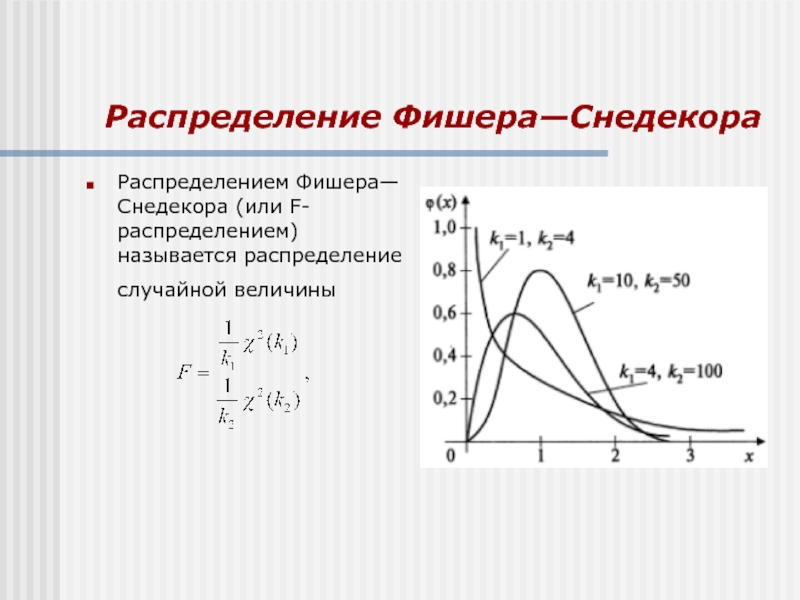
Слайд 14Распределение Фишера—Снедекора
Распределением Фишера—Снедекора (или F-распределением) называется распределение случайной величины
Слайд 15Проверка гипотез о виде распределения
Слайд 16-критерий Пирсона
В наиболее часто используемом на практике
критерии- Пирсона в качестве меры расхождения U берется
величина , равная сумме квадратов отклонений частостей (статистических вероятностей) от гипотетических рассчитанных по предполагаемому распределению, взятых с некоторыми весами :
Слайд 17Схема применения критерия для проверки гипотезы
1. Определяется
мера расхождения эмпирических и теоретических частот по
.
2. Для выбранного уровня значимости а по таблице
-распределения находят критическое значение при числе степеней свободы k=m-r-1.
3. Если фактически наблюдаемое значение больше критического, т.е. > , то гипотеза отвергается, если , гипотеза
не противоречит опытным данным.
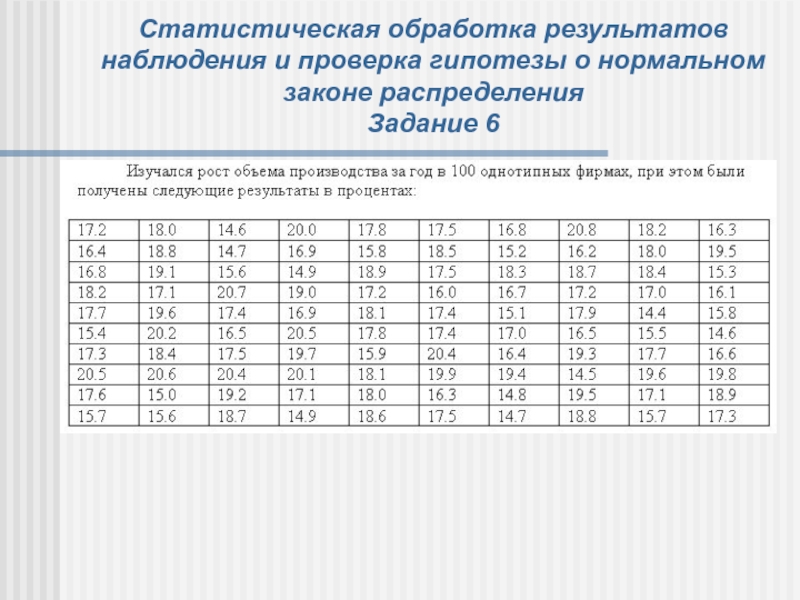
Слайд 18Статистическая обработка результатов наблюдения и проверка гипотезы о нормальном законе
распределения
Задание 6
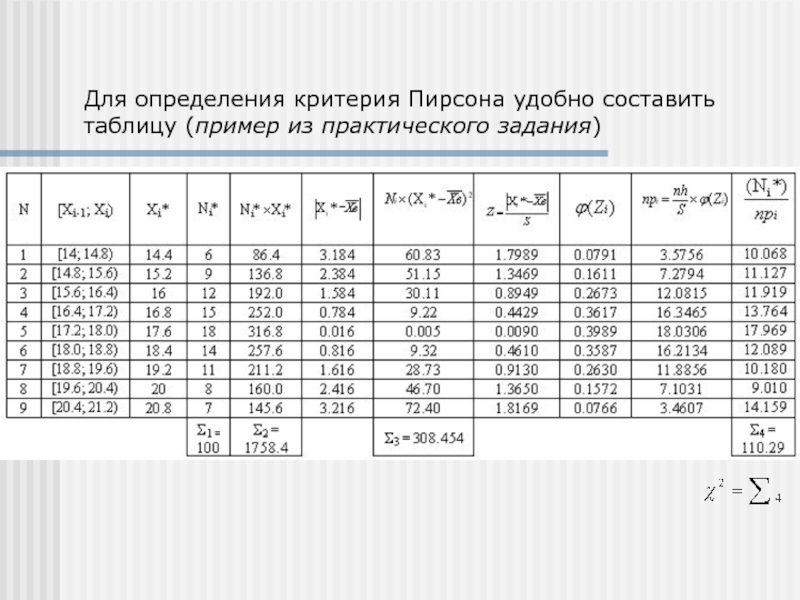
Слайд 19Для определения критерия Пирсона удобно составить таблицу (пример из практического
задания)
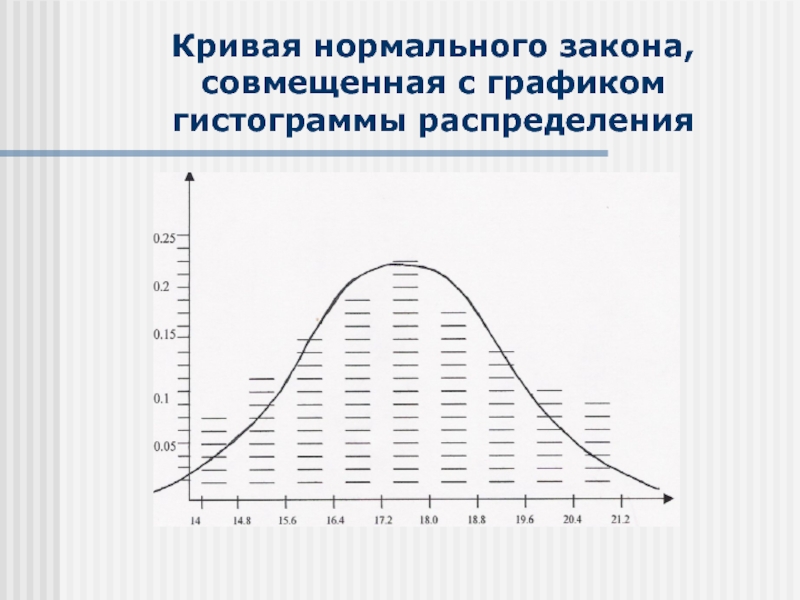
Слайд 20Кривая нормального закона, совмещенная с графиком гистограммы распределения



![Курсовая работа на тему: Статистическая обработка результатов испытаний и Равномерный закон распределенияНепрерывная случайная величина X имеет равномерный закон распределения на Равномерный закон распределенияНепрерывная случайная величина X имеет равномерный закон распределения на отрезке [а, b], если ее плотность](/img/thumbs/5b80bacae471bcc18f6a75e1851099be-800x.jpg)