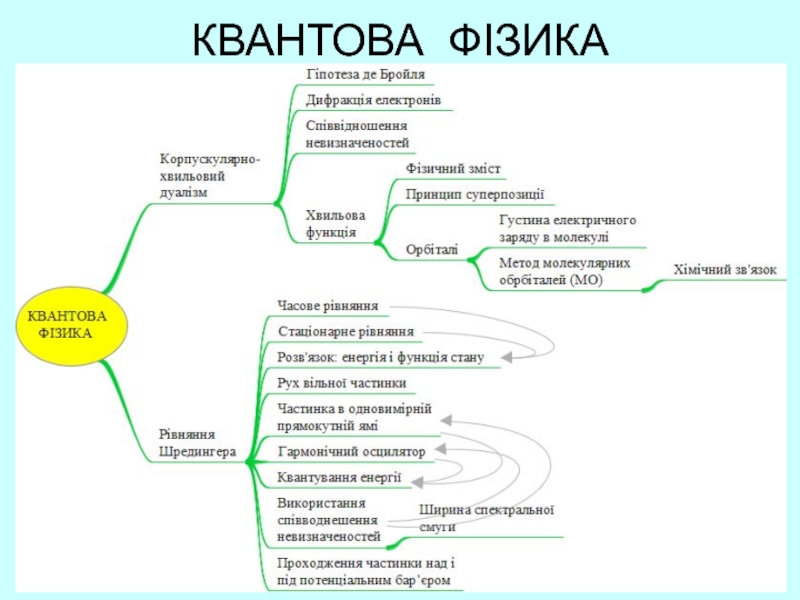
Слайд 2Корпускулярно-хвильовий дуалізм.
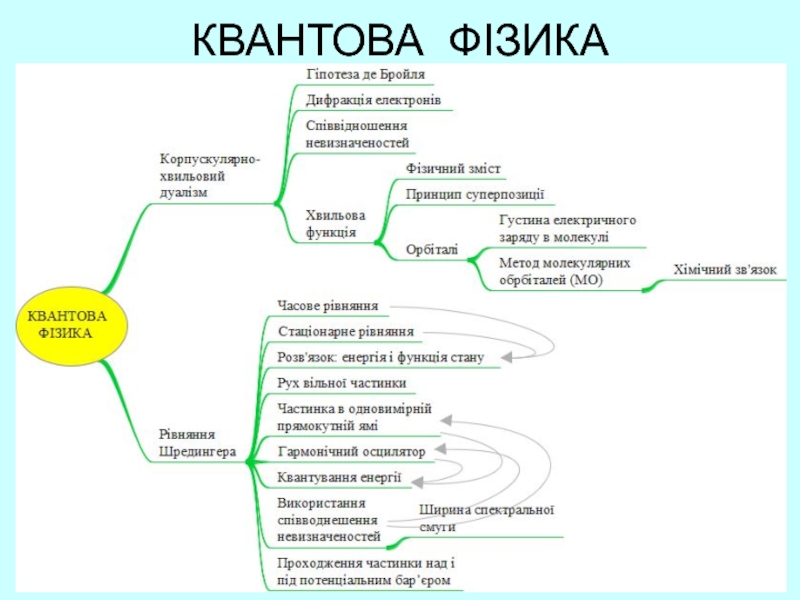
Рівняння Шредингера
1. Гіпотеза де-Бройля.
2. Дифракція електронів.
3. Співвідношення
невизначеностей.
4. Часове і стаціонарне рівняння Шредингера.
5. Квантування енергії.
6. Хвильова функція
(орбіталь). Фізичний зміст.
7. Приклади застосування.
Слайд 3Формула де-Бройля
Оскільки світло проявляє корпускулярно-хвильовий дуалізм, Луї де-Бройль в 1924
р. висунув гіпотезу, що і елементарні частинки будуть проявляти не
лише корпускулярні, а і хвильові властивості.
Для фотона
За де-Бройлем для частинки існує такий же зв'язок, тобто
Слайд 4Формула де-Бройля
Якщо нерелятивістська частинка має кінетичну енергію
Тоді
Отже, для електронів, розігнаних
до 1÷100 еВ матимемо довжину хвилі, характерну для рентгенівських спектрів.
Експеримент
Девісона і Джермера з розсіювання електронів на монокристалі Ni (1927 р.) підтвердив висновки теорії де-Бройля.
Слайд 5Формула де-Бройля
Подивимось з позицій корпускулярно-хвильового дуалізму на атом водню.
Згідно з
другим постулатом Бора mrn = nħ. Звідси
Отже, на
довжині стаціонарної орбіти вкладається ціле число довжин хвиль λ. Інтерференція хвилі де-Бройля на орбіті дає інтерференційний максимум, що і забезпечує стаціонарність орбіти.
Слайд 7Формула де-Бройля
При проходженні окремих електронів через тонкий монокристал отримуємо дифракційну
картину. Отже, хвильові властивості притаманні окремому електрону.
Таким чином, електрон –
не маленька кулька. Він має складну структуру з корпускулярно-хвильовими властивостями.
Хвильові властивості мають і всі інші елементарні частинки. В 1929 р. Штерн дослідив дифракцію атомів і молекул. Пізніше дослідили хвильові властивості нейтрона.
Для важких тіл виявити хвильові властивості неможливо. Наприклад, для маси m = 1 г при v = 100 м/с λ=6,62·10-33 м.
Слайд 8Співвідношення невизначеностей
Розглянемо обмеження, які накладає корпускулярно-хвильовий дуалізм на можливість одночасного
визначення імпульсу та координати частинок і фотонів.
Хвильові властивості частинки спричинюють
відсутність чіткої траєкторії її руху і неправомірність говорити про одночасне визначення імпульсу і координати. Хвиля заповнює певну область простору і не може локалізуватись в точку.
Якщо фотон має точно відомий імпульс, тобто Δр=0, йому відповідає не обмежена в просторі хвиля з λ= h/p. Отже, просторовий інтервал Δх →∞. Якщо ж область локалізації фотона обмежена (Δх обмежена), тоді це не монохромати-чна хвиля, а група хвиль, причому Δр=Δ(h/λ).
Слайд 9Співвідношення невизначеностей.
Такі ж висновки справедливі і для частинок. В 1927
р. В.Гейзенберг знайшов співвідношення
Добуток невизначеностей координати і відповідного їй
імпульсу не може бути меншим від ħ.
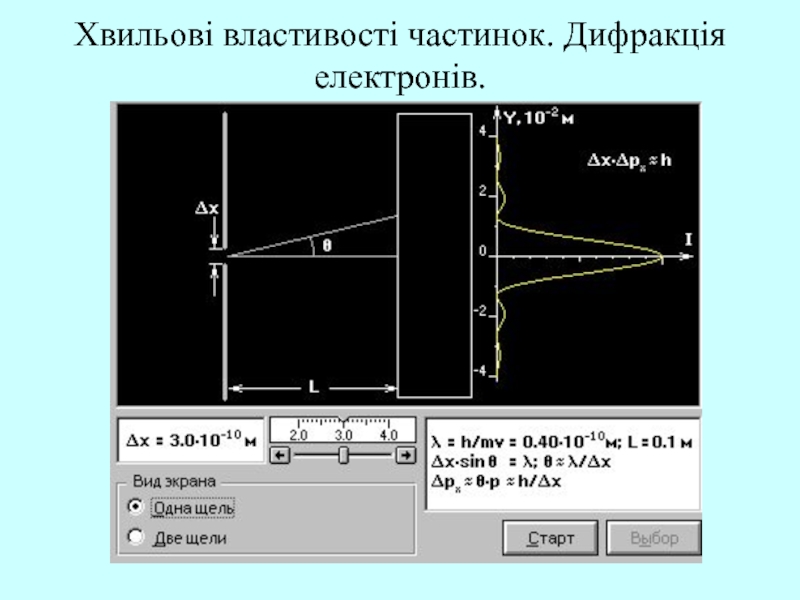
Нехай потік електронів проходить через вузьку щілину Δх, розміщену напрямку руху електронів. Відбудеться дифракція, яка спостерігається на екрані. В момент проходження через щілину координата визначається з точністю Δх. Внаслідок дифракції Δрх = p·sinφ, Δх·sinφ=λ, отримаємо Δх· Δрх = h.
Слайд 10Хвильові властивості частинок. Дифракція електронів.
Слайд 11Співвідношення невизначеностей
Розглянемо електрон в атомі. Його положення визначається з точністю
до розмірів атома Δх ~ 10-10 м. В цьому випадку
З класичної фізики v = 2,3·106 м/с. Отже, Δv одного порядку з v, тому не можна говорити про рух по певній траєкторії і не можна користуватись законами класичної фізики.
Можна записати
Система, що має час життя Δt, не може мати чіткого значення енергії. Тому і для частоти фотона ν±ΔE/h.
Слайд 12Хвильова функція
Потрібно з'ясувати фізичну природу хвиль де-Бройля. Порівнювали дифракцію світла
і мікрочастинки.
Для світла в результаті інтерференції є ослаблення чи
підсилення амплітуди, а інтенсивність ~A2.
З точки зору корпускулярної теорії інтенсивність пропорційна числу фотонів в даній точці дифракційної картини. Тобто, для кожного фотона квадрат амплітуди визначає ймовірність потрапляння фотона в ту чи іншу точку.
Дифракція електронів аналогічна. Наявність максимумів свідчить про найбільшу інтенсивність хвиль де-Бройля. З іншого боку, інтенсивність більша там, де більше число електронів.
Слайд 13Хвильова функція
Отже, дифракційна картина є проявом статистичної закономірності, згідно з
якою частинки потрапили в ті місця, де інтенсивність хвиль де-Бройля
найбільша.
В 1926 р. Борн припустив, що за хвильовим законом змінюється не сама ймовірність знаходження електрона, а амплітуда ймовірності, яка позначається (x,y,z,t). Цю величину називають хвильовою функцією. Амплітуда може бути комплексною, а ймовірність пропорціональна квадрату модуля функції:
Ймовірність знайти частинку в об'ємі dV:
Слайд 14Хвильова функція
Звідси
− умова нормування хвильової функції.
Щоб функція була
характеристикою стану частинки,
необхідно:
1) Функція повинна бути скінченною, однозначною і
неперервною.
2) Похідні повинні бути неперервними.
3) Функція повинна бути інтегрованою.
Слайд 15Хвильова функція
Якщо система може знаходитись в станах 1, 2, ...,
n, то вона може бути і в стані , який
є суперпозицією інших станів:
За допомогою функції в квантовій механіці можна обчислити середні значення фізичних величин, які характеризують певний об'єкт. Наприклад, можна обчислити середню відстань від електрона до ядра в атомі:
Слайд 16Хвильова функція
Одноелектронну хвильову функцію в сферично симетричному електричному полі атомного
ядра, яку задають головним n, орбітальним l і магнітним m
квантовими числами, називають ще атомною орбіталлю.
Назва «орбіталь» (а не орбіта) відображає геометричне уявлення про стаціонарні стани електрона в атомі; така особлива назва відображає той факт, що стан електрона в атомі описується законами квантової механіки і відрізняється від класичного руху по траєкторії.
Сукупність атомних орбіталей з однаковим значенням головного квантового числа n складає одну електронну оболонку.
Слайд 17Хвильова функція
Геометричне уявлення атомної орбіталі – область простору, обмежена поверхнею
рівною густини (еквіденсітною поверхнею) ймовірності або заряду. Густину ймовірності на
граничній поверхні вибирають виходячи з задачі, що розв'язують, але, зазвичай, таким чином, щоб ймовірність знаходження електрона в обмеженій області лежала в діапазоні значень 0,9-0,99.
Оскільки енергія електрона визначається кулонівською взаємодією і, отже, відстанню від ядра, то головне квантове число n задає розмір орбіталі.
Слайд 18Хвильова функція
Орбіталі слетеровського типу мають наступний вигляд:
де
A − коефіцієнт норміровки
− сферична гармоніка
n*
− ефективне квантове число, параметр, який залежить від головного квантового числа n і визначається емпірично
r − відстань між електроном і ядром
− орбітальна експонента
Z − заряд ядра, s − константа екранування
Співвідношення значень n* і n
n 1 2 3 4 5 6
n* 1 2 3 3,7 4 4,2
Слайд 19Густина електричного заряду
У квантовій механіці густина заряду, наприклад,
електрона в
атомі, співвідноситься з хвильової функцією
з допомогою наступного співвідношення:
причому хвильова
функція повинна мати нормування:
Слайд 20Метод МО ЛКАО
Молекула розглядається як ціле, а не як сукупність
атомів, що зберегли індивідуальність.
Всі електрони даної молекули (як і в
атомі) розподіляються за відповідними орбіталями.
Хвильова функція ψ, яка залежить від чотирьох квантових чисел, що має конкретний математичний вигляд і задовольняє умові нормування і однозначності, називається молекулярної орбіталью (МО) (за аналогією з атомною).
Кожна орбіталь характеризується своїм набором квантових чисел, що відображають властивості електронів в даному енергетичному стані. На відміну від одноцентрових орбіталей атомів, орбіталі молекул багатоцентрові, тобто молекули мають спільні орбіталі для двох або більше атомних ядер. Кожна молекулярна орбіталь має певну енергію, що наближено характеризується відповідним потенціалом іонізації.
Слайд 21ОРБІТАЛЬ – область найбільш можливого місцезнаходження електрона в атомі (атомна
орбіталь) або в молекулі (молекулярна орбіталь). Електрон рухається в атомі
навколо ядра не по зафіксованій лінії-орбіті, а займає деяку область простору.
Орбіталь електрона у атома водню
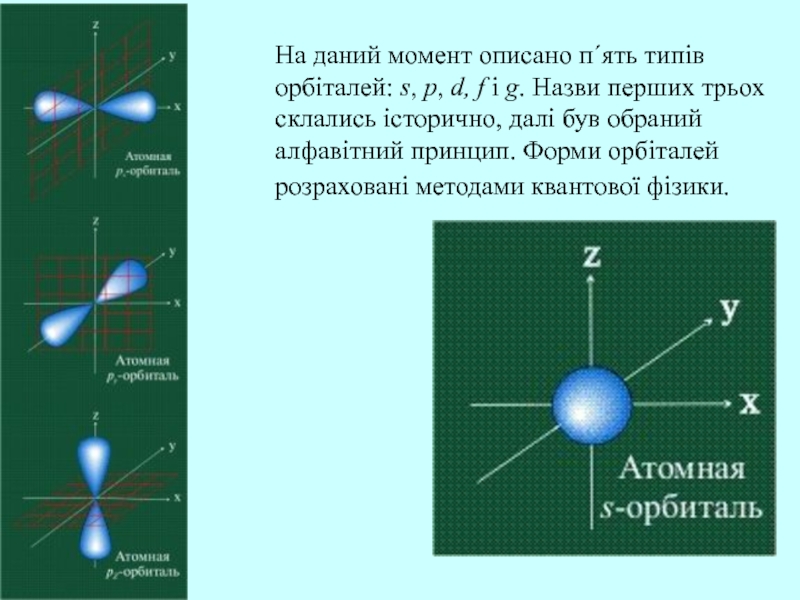
Слайд 22На даний момент описано п΄ять типів орбіталей: s, p, d,
f і g. Назви перших трьох склались історично, далі був
обраний алфавітний принцип. Форми орбіталей розраховані методами квантової фізики.
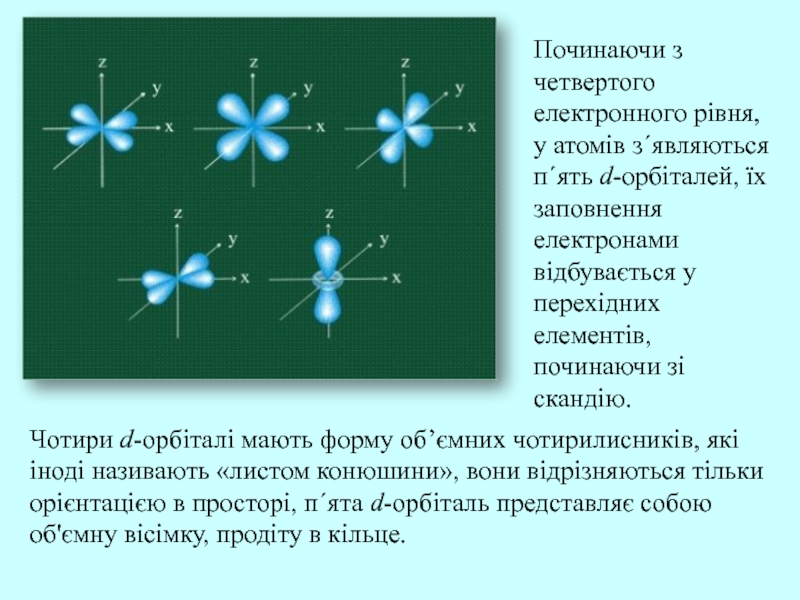
Слайд 23Чотири d-орбіталі мають форму об’ємних чотирилисників, які іноді називають «листом
конюшини», вони відрізняються тільки орієнтацією в просторі, п΄ята d-орбіталь представляє
собою об'ємну вісімку, продіту в кільце.
Починаючи з четвертого електронного рівня, у атомів з΄являються п΄ять d-орбіталей, їх заповнення електронами відбувається у перехідних елементів, починаючи зі скандію.
Слайд 24В тому випадку, коли атом вуглецю бере участь в утворенні
насичених сполучень (які не мають кратних зв’язків), одна s-орбіталь і
три р-орбіталі з΄єднуються, утворюючи нові орбіталі, що являють собою гібриди початкових орбіталей (процес називають гібридизацією). Кількість гібридних орбіталей завжди рівна кількості вихідних. Отримані орбіталі-гібриди однакові за формою та зовні нагадують асиметричні об'ємні вісімки.
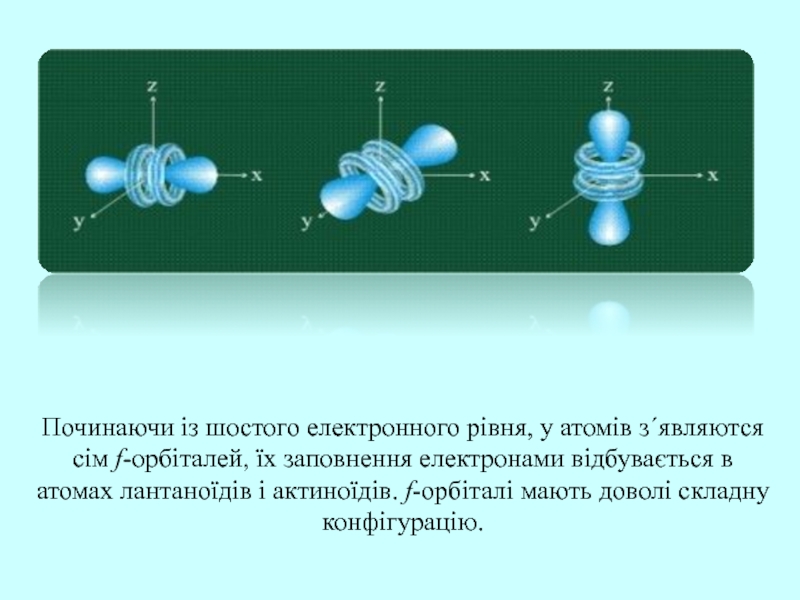
Слайд 25Починаючи із шостого електронного рівня, у атомів з΄являются сім f-орбіталей,
їх заповнення електронами відбувається в атомах лантаноїдів і актиноїдів. f-орбіталі
мають доволі складну конфігурацію.
Слайд 26На восьмому електронному рівні знаходяться дев΄ять
g-орбіталей. Елементи, які мають
електрони на цих орбіталях, повинні з'явитися у восьмому періоді, поки
вони недоступні (найближчим часом очікується отримання елементу №118, останнього елементу сьомого періоду Періодичної системи), його синтез проводять в Об’єднаному інституті ядерних досліджень в Дубні.
Слайд 27Хімічний зв’язок
Хімічний зв'язок притягання між атомами або молекулами дозволяє утворення
хімічних сполук, які містять два або більше атомів.
Хімічний зв'язок
викликається залученням електромагнітної сили між протилежними зарядами, або між електронами і ядрами, або в результаті дипольного притягання.
Міцності зв'язків значно варіюють. Є "сильні зв'язки", такі як ковалентний або іонний зв'язок, і "слабкі зв'язки", такі як диполь-дипольна взаємодія, дисперсійні і водневі зв'язки.
Слайд 35Квантово-механічні задачі
1. Рівняння Шредінґера
2. Рух вільної частинки.
3. Частинка в одновимірній
прямокутній потенціальній ямі.
4. Тунельний ефект.
5. Гармонічний осцилятор
6. Використання співвідношення невизначеностей
Слайд 36Рівняння Шредінгера
Хвилі де-Бройля мають статистичне трактування. Цей факт та співвідношення
невизначеностей вимагають, щоб рівняння руху в квантовій механіці було хвильовим.
Рівняння повинно бути відносно ψ(x,y,z,t), оскільки саме величина |ψ|2 визначає ймовірність перебування частинки в момент часу t в об'ємі dV.
Таке рівняння запропонував (постулював) Шредінгер у 1926 р.
Правильність цього рівняння підтверджується експериментально.
Слайд 37Рівняння Шредінгера
Таке рівняння справедливе для довільної частинки з v
вільну частинку, якій відповідає хвиля
Враховуючи, що
запишемо
Слайд 38Рівняння Шредінгера
Знайдемо похідні
Звідси
Ці дані підставимо в формулу
Слайд 39Рівняння Шредінгера
Такий же вигляд має рівняння Шредінгера при U =
0.
Якщо існує силове поле, тоді повна енергія Е складається з
кінетичної і потенціальної енергії. Тоді
Підставивши, отримаємо повне рівняння Шредінгера.
Ми записали рівняння Шредінгера, що залежить від часу.
Проте, часто використовують стаціонарне рівняння.
Слайд 40Стаціонарне рівняння Шредінгера
Шукаємо розв'язок у вигляді
Підставивши в рівняння Шредінгера, отримаємо
Це
і є стаціонарне рівняння Шредінгера. Функції ψ, які
задовольняють рівняння
при певній величині Е, назива-
ються власними функціями.
Розв'язок існує не при довільних Е, а лише при певних.
Слайд 41Рух вільної частинки
Застосуємо рівняння Шредінгера до руху вільної частинки.
Енергія E
= Ek. Частинний розв'язок:
Повний розв'язок:
Слайд 42Рух вільної частинки
Маємо суперпозицію двох плоских хвиль однакової частоти ω
= Е/ħ. Порівняння з виразом для плоскої хвилі
дає
Отже, вільній
частинці відповідає плоска монохроматична
хвиля де-Бройля. Власні значення енергії
можуть мати довільне значення. Енергетичний спектр
неперервний.
Слайд 43Рух вільної частинки
Ймовірність знайти частинку в певній точці простору
Отже,
як і слід чекати для монохроматичної хвилі, вона повністю делокалізована.
Для реальної частинки її делокалізація неможлива. Отже, буде не монохроматична хвиля, а група хвиль.
Слайд 44Частинка в одновимірній прямокутній потенціальній ямі
Розглянемо прямокутну потенціальну яму, для
якої
Рівняння Шредінгера
Яма має безмежно високі стінки, тому ймовірність знайти
частинку
за межами ями дорівнює нулю. Отже
Слайд 45Частинка в одновимірній прямокутній потенціальній ямі
В межах ями
Розв'язок
Оскільки
(0) = 0, то В = 0.
Отже,
Умова (ℓ) =
0 виконується при kℓ = nπ, n – цілі числа.
Слайд 46Частинка в одновимірній прямокутній потенціальній ямі
Для n = 1
− максимум ймовірності знаходиться в центрі ями. Для n = 2 в центрі |2|2 =0. Оскільки
Слайд 47Частинка в одновимірній прямокутній потенціальній ямі
Різниця енергій двох сусідніх рівнів
збільшується зі збільшенням n.
Якщо яма широка, наприклад, ℓ =
0,1 м, тоді
Тобто, рівні лежать так тісно, що утворюють неперервний
спектр. Якщо ж ℓ = 10-10 м, то ΔEn = (2n+1)·37 еВ.
Тепер дискретність рівнів значна.
Слайд 48Гармонічний осцилятор
Хвильове рівняння, яке описує гармонічний осцилятор, має вигляд:
Розв’язком цього
рівняння є: En = ћ0(n+½), n = 1,2,3,…
де , , Hn() – поліном Ерміта, n = 0, 1, 2, .
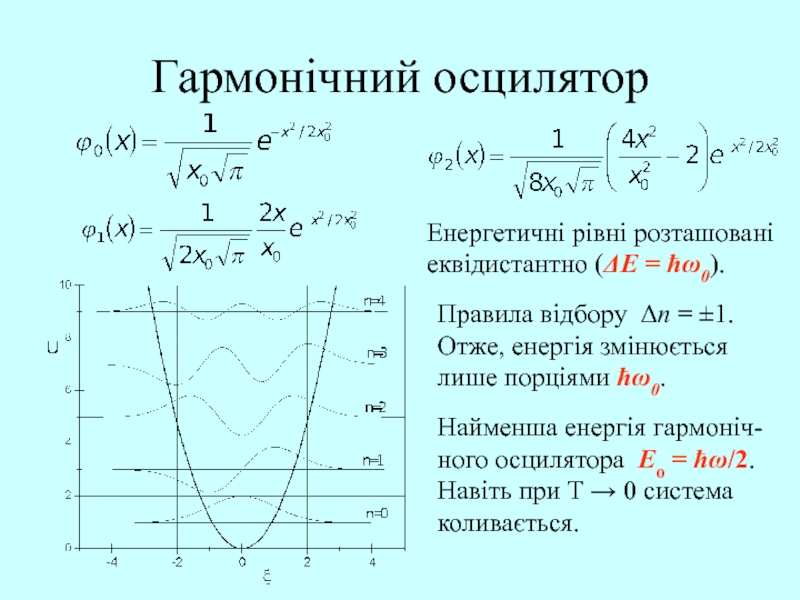
Слайд 49Гармонічний осцилятор
Енергетичні рівні розташовані
еквідистантно (E = ћ0).
Правила відбору
Δn = 1.
Отже, енергія змінюється
лише порціями ћ0.
Найменша
енергія гармоніч-
ного осцилятора Eo = ħω/2.
Навіть при Т → 0 система
коливається.
Слайд 50Використання співвідношення невизначеностей
Розрахуємо співвідношення невизначеностей для розрахунку енергій в
одновимірній потенціальній ямі та для гармонічного осцилятора.
У випадку одновимірної потенціальної
ями: Δp = p, Δx = ℓ
ΔpΔx =pℓ = πħ p = πħ/ℓ.
Слайд 51Використання співвідношення невизначеностей
Тепер розрахуємо енергію гармонічного осцилятора:
Звідси
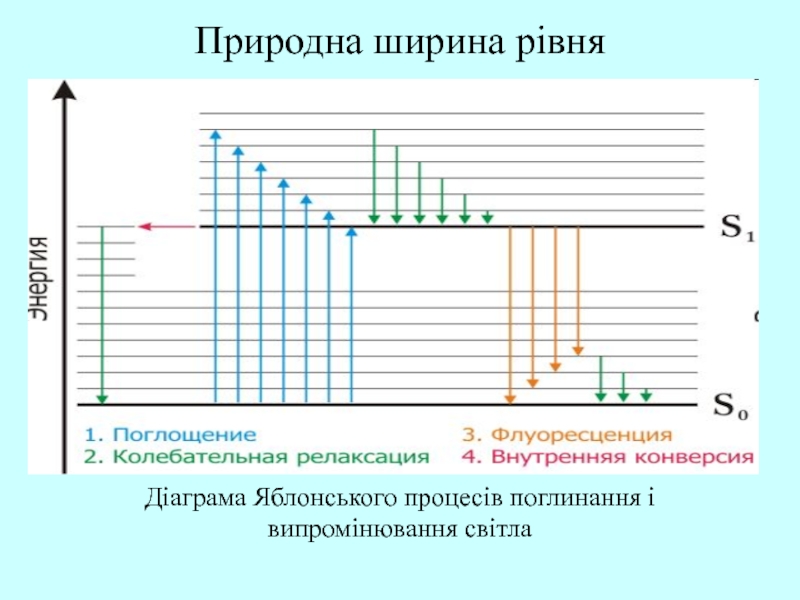
Слайд 53Природна ширина рівня
Діаграма Яблонського процесів поглинання і
випромінювання світла
Слайд 54Схема енергетичних рівнів та електронних переходів при резонансній (а), спонтанній
(б) і вимушеній (в) люмінесценції:
1 - основний рівень;
2, 3 -
збуджені рівні;
4 - метастабільний рівень;
↑ - поглинання;
↓ - люмінесценція;
- безвипромінювальної перехід
Схема енергетичних рівнів та електронних переходів при поглинанні та люмінесценції між рівнями з різним часом життя стану
Природна ширина рівня
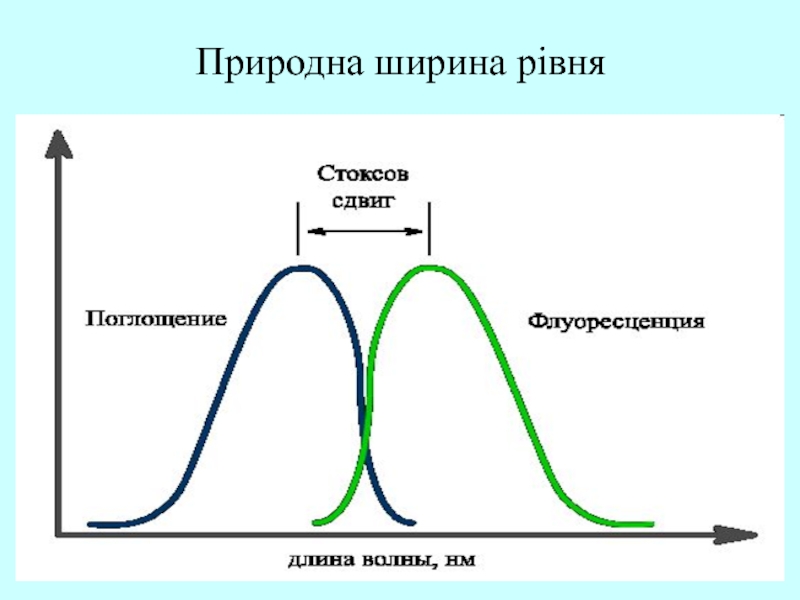
Слайд 55Природна ширина рівня
ШИРИНА РІВНЯ – невизначеність енергії квантово-механічної системи (атома,
молекули та ін), що має дискретні рівні енергії в стані,
якій не є строго стаціонарним.
Ширина рівня ΔЕ, що характеризує розмиття рівня енергії, його розширення, залежить від середньої тривалості перебування системи у цьому стані – часу життя на рівні Δτ і, згідно співвідношенню невизначеностей для енергії і часу ΔЕ = ћ/ Δτ
Для суворо стаціонарного стану системи Δτ = ∞ і ΔЕ = 0.
Слайд 56Природна ширина рівня
Час життя Δτ, а отже, і ширина рівня
обумовлені можливістю квантових переходів системи в стани з іншими енергіями.
Для
вільної системи (напр., для ізольованого атома) спонтанні випромінювальні переходи з рівня на нижні рівні визначають радіаційну, або природну, ширину рівня:
ΔЕ = Аkћ,
де Ak = ΣAki – повна ймовірність спонтанного випускання з рівня,
Aki - коефіцієнт Ейнштейна для спонтанного випускання.
Слайд 57Тунельний ефект
Розглянемо бар'єр прямокутної форми на
шляху руху частинок.
В класичній фізиці
частинка з E > U пройде
над бар'єром, а з E
< U відіб'ється.
Для мікрочастинки навіть при E > U існує відбивання частинки, а при E < U є ймовірність того, що частинка проникне через бар'єр.
Слайд 58Тунельний ефект
Для областей 1 і 3
Для області 2
Розв'язок
В області 3 є лише хвиля, яка пройшла через бар'єр,
тобто
Слайд 59Тунельний ефект
Для випадку E < U
Тому в області
2
Це не плоска хвиля (показники не уявні). Величина В2 =
0,
за умовою скінченності.
Слайд 60Тунельний ефект
Ймовірність проходження електрона через бар'єр (коефі-цієнт прозорості) дорівнює
Щоб
знайти величину D, необхідно використати умову
неперервності функції у
всій області змін х. Отже,
1(0) = 2(0), 2(ℓ) = 3(ℓ). Щоб функція була гладкою,
необхідно, щоб і похідні були неперервними.
Якщо В1 = 0, то А1 = А2,
Слайд 61Тунельний ефект
Тепер знайдемо D
Для бар'єра довільної форми
З формули випливає, що
величина D залежить від маси
мікрочастинки, ширини бар'єра і різниці
(U – E).
Слайд 62Тунельний ефект
Тунелювання є квантовим ефектом, який існує внаслідок співвідношення невизначеностей.
Невизначеність Δр на відрізку Δх = ℓ Δp >h/ℓ.
Цьому відповідає невизначеність кінетичної енергії (р ± Δр)2/2m, якої може бути достатньо для подолання бар'єра.
Експеримент підтверджує тунельний ефект:
− холодна емісія електронів з металу,
− радіоактивний α-розпад,
− перебіг термоядерних реакцій тощо.
Слайд 63Е́рвін Шре́дінґер
(Erwin Schrödinger 12.08.1887 – 04.01.1961)
Австрійський фізик-теоретик, один із
засновників квантової механіки. Нобелівська премія з фізики 1933 р.
Навчався
у Віденському університеті. Працював у Цюріхському, Вроцлавському, Берлінському та Оксфордському університетах.
Розробив квантову механіку та хвильову теорії матерії. Він довів еквівалентність його теорії матричній механіці Гейзенберга.