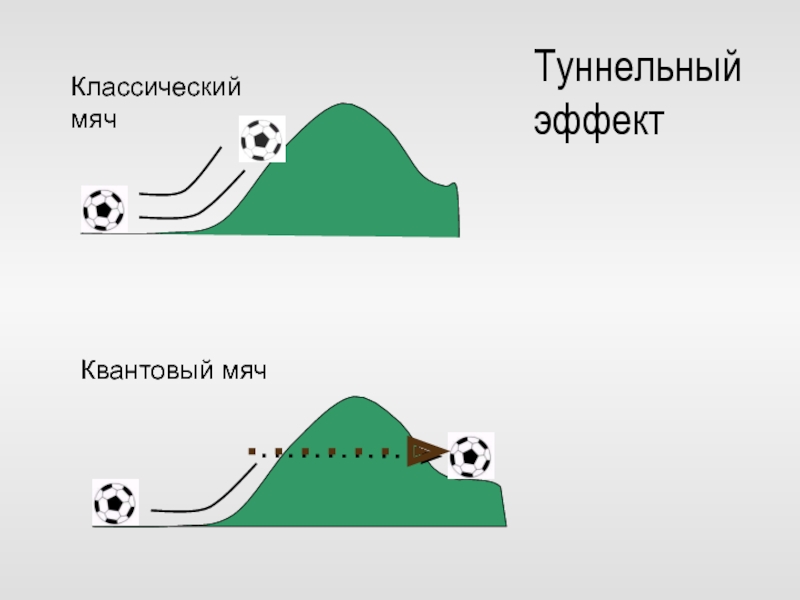
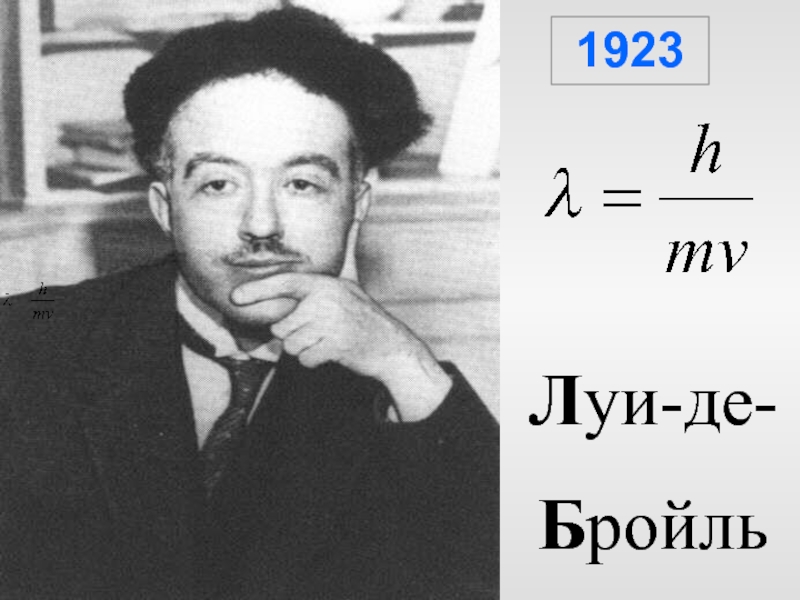Слайд 1Квантовая механика и строение атома
Концепции современного естествознания
Лекция 5
Слайд 2Фундаментальные физические теории
Механика
Электродинамика
Слайд 3В основании квантовой механики лежит несколько новых принципов
Слайд 4Философские следствия квантовой механики
Эйнштейн ввел в теорию наблюдателя.
В результате пришлось
отказаться от абсолютности и независимости пространства и времени
Квантовая механика вводит
и воздействие наблюдателя на объект: в результате наблюдения объект меняется.
Итогом стал отказ от причинности в форме детерминизма и переход к вероятностной модели мира.
Слайд 5Было время, когда газеты сообщали, что только двенадцать человек понимают
теорию относительности.
Я не верю, что такое время когда-либо было.
С другой стороны, я думаю, что могу совершенно спокойно сказать, что квантовую механику не понимает никто
Ричард Фейнман
Слайд 6Новые теории возникают, когда есть противоречия
Между двумя старыми теориями
Между теорией
и экспериментами
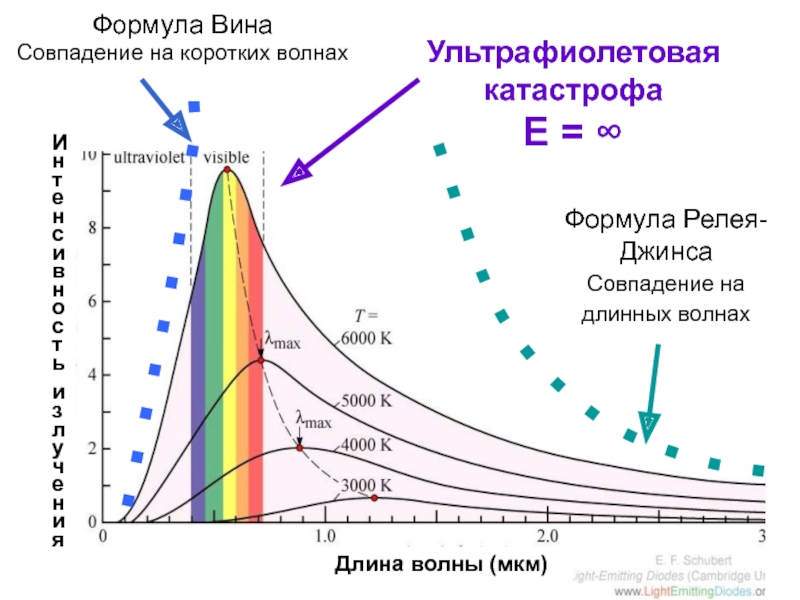
Слайд 7Кризис физики на рубеже веков 19 – 20
Противоречие между
предсказанием электромагнетизма
в задаче об излучении тел
и здравым смыслом
вкупе с экспериментальными данными
Слайд 8С чего все началось
Задача об излучении тел
Была важна для исследования
звезд
Слайд 9Тепловое излучение – это электромагнитное излучение испускаемое телами за счет
своей внутренней энергии.
Возникает за счет столкновений молекул при движении
пропорционально температуре
Слайд 11Существует минимальная порция энергии для каждой длины волны
Чем больше энергия
волны, тем больше эта порция
Если энергия, которая должна излучаться на
данной длине, окажется меньше этой порции, то излучение волн такой длины невозможно
Квант энергии маленький
Слайд 12Постоянная Планка
γ-лучи – энергия кванта в миллион раз больше
Можно поднять
на 1 сантиметр массу в 10–13 грамма (1011 нейтронов)
Слайд 13Определение
Квантованными называются физические величины, которые могут принимать лишь определенные дискретные
значения
Слайд 14Это подобно тому, как если бы природа разрешала либо пить
целый литр пива, либо не пить совсем, не допуская никаких
промежуточных доз
Георгий Гамов
Почему это так, никто не знал
Слайд 15Дискретность в истории физики
Дискретность вещества – атомистика Демокрита
5 в. до
н.э.
Дискретность электрического заряда – Томсон
конец 19 в.
Дискретность света 1
– Ньютон
Дискретность света 2 – Эйнштейн
17 в.
1905
Дискретность энергии – Планк
1900
Слайд 16Дискретность электрического заряда – открытие электрона
1870-80-е годы
Дж.Стони и Г.Гельмгольц
высказывают идею об «атомах электричества». Термин электрон
1897
Джозеф Томсон
в Кавендишской лаборатории (основана Максвеллом) открывает минимальный электрический заряд и его носителя – электрон
Слайд 181. Что атомы не неделимы, так как из них
могут быть вырваны отрицательно заряженные частицы под действием электрических сил,
удара быстро движущихся частиц, ультрафиолетового света или тепла.
2. Что эти частицы все одинаковой массы, несут одинаковый заряд отрицательного электричества, от какого бы рода атомов они ни происходили, и являются компонентами всех атомов.
3. Масса этих частиц меньше, чем одна тысячная массы атома водорода. Я вначале назвал эти частицы корпускулами, но они теперь называются более подходящим именем «электрон».
Выводы Томсона
Дж.Дж. Томсон
Слайд 19Примечание. Дробный электрический заряд (⅓, ⅔) приписывают кваркам – элементарным частицам,
тройки которых образуют протоны и нейтроны
Однако никто пока не наблюдал
отдельно существующего кварка.
е = 1.6·10-19 Кл.
Заряд электрона
Любой другой заряд равен целому числу элементарных зарядов e.
Таким образом, заряд дискретен
q = ± ne
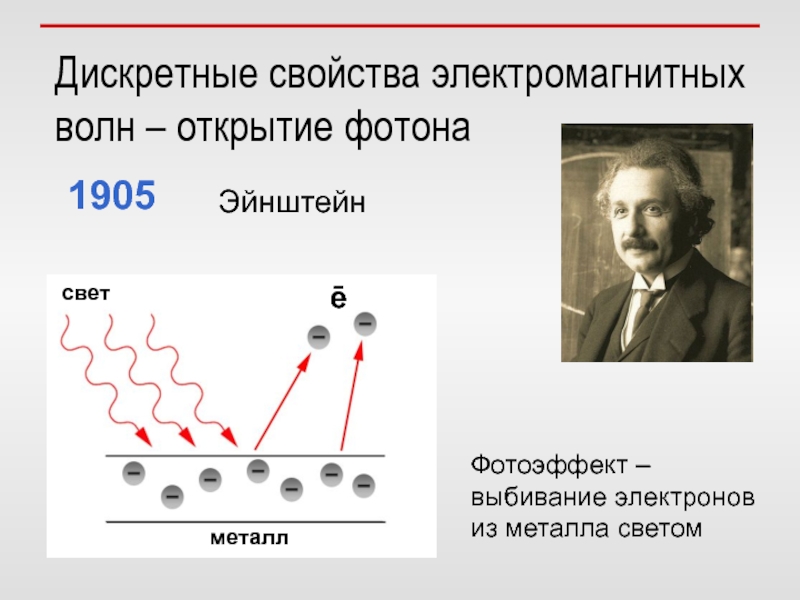
Слайд 20Дискретные свойства электромагнитных волн – открытие фотона
1905
Эйнштейн
Фотоэффект – выбивание
электронов из металла светом
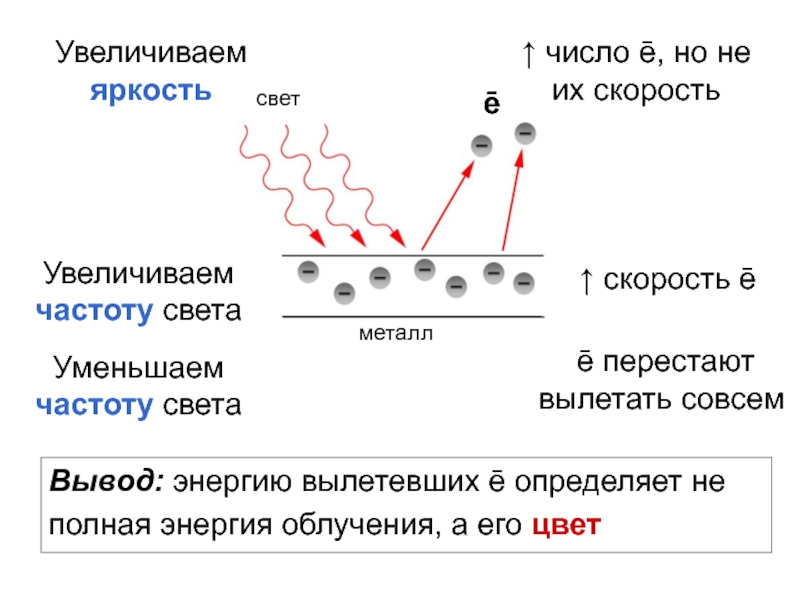
Слайд 21Увеличиваем яркость
↑ число ē, но не их скорость
Увеличиваем частоту света
↑
скорость ē
Уменьшаем частоту света
ē перестают вылетать совсем
Вывод: энергию вылетевших
ē определяет не полная энергия облучения, а его цвет
Слайд 22Энергия не только излучается, но и поглощается квантами
Вывод Эйнштейна
Корпускулярная
модель света
Свет состоит из частиц – фотонов
Энергия фотона
с частотой ν
Уравнение фотоэффекта:
Слайд 23Нобелевскую премию в 1921 Эйнштейн получил именно за фотоэффект!
Слайд 24Переходный период от классической физики к квантовой
Модели строения атома
Слайд 25Открытие радиоактивности
Антуан Беккерель
1896
Пьер и Мария Кюри
1898
уран
Слайд 26Радиоактивный распад – это распад ядер атомов с превращением их
в другие элементы
-частицы – ядра гелия 2p +
2n
-частицы – электроны
-лучи – коротковолновое электромагнитное излучение <10–10 м
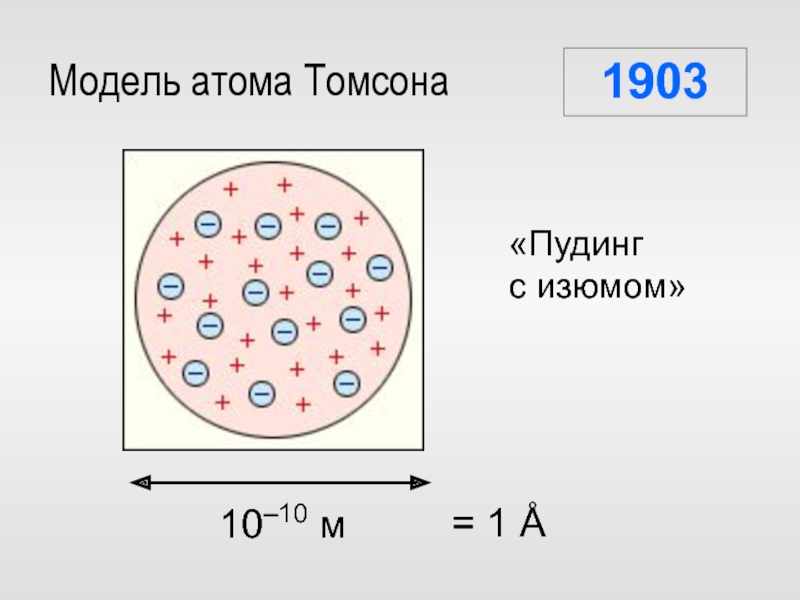
Слайд 27Модель атома Томсона
1903
«Пудинг
с изюмом»
10–10 м
= 1 Å
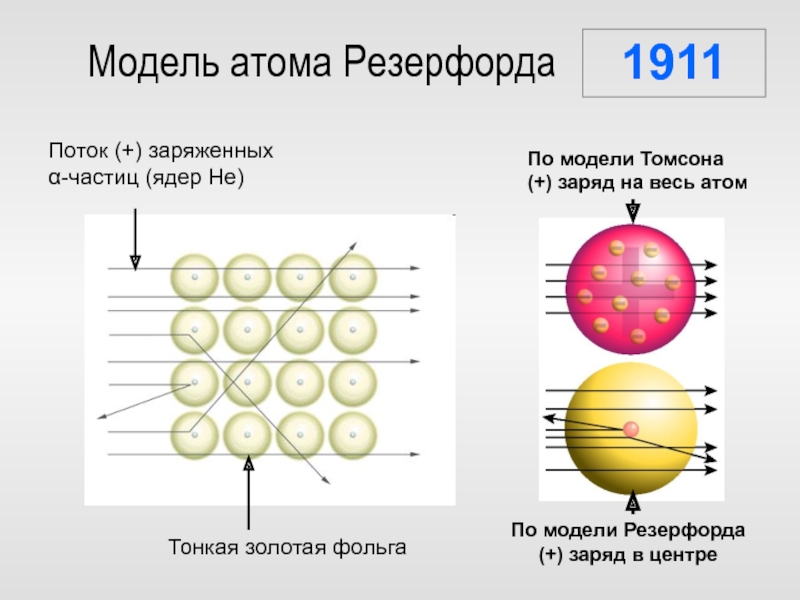
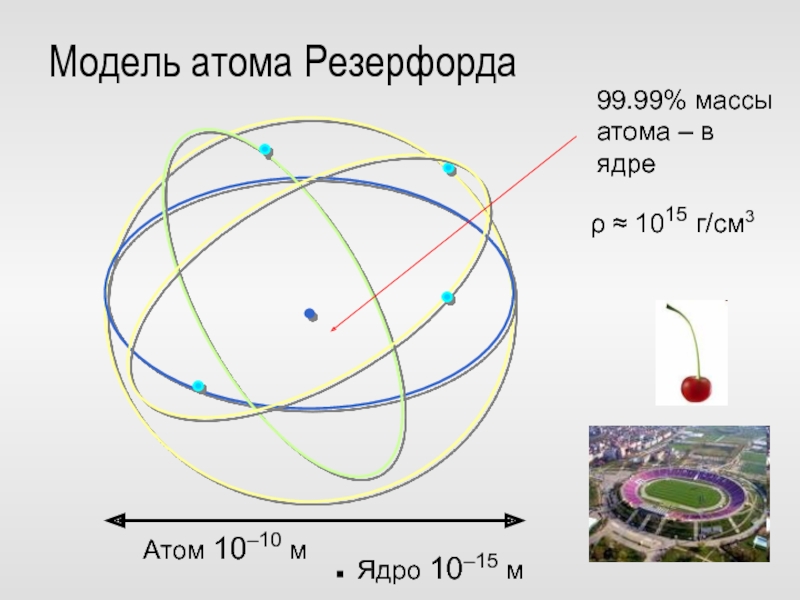
Слайд 29Модель атома Резерфорда
ρ ≈ 1015 г/см3
Атом 10–10 м
Ядро 10–15
Слайд 30Проблема с атомом Резерфорда
Электроны движутся с ускорением
когда она кончится, упадут
на ядро
должны излучать энергию
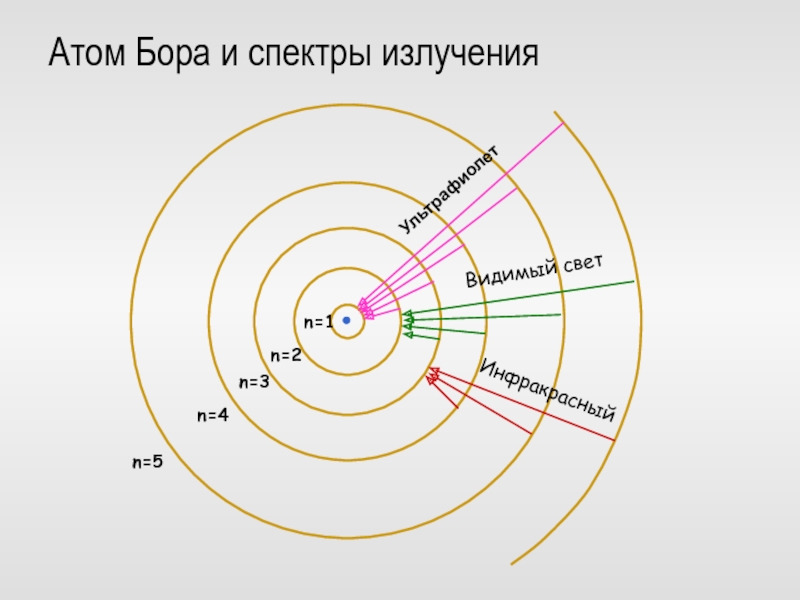
Слайд 31Модель атома Бора
квантовый принцип разрешенных орбит
Нильс Бор 1885 – 1962
1913
Институт
теоретической физики Бора при Копенгагенском университете
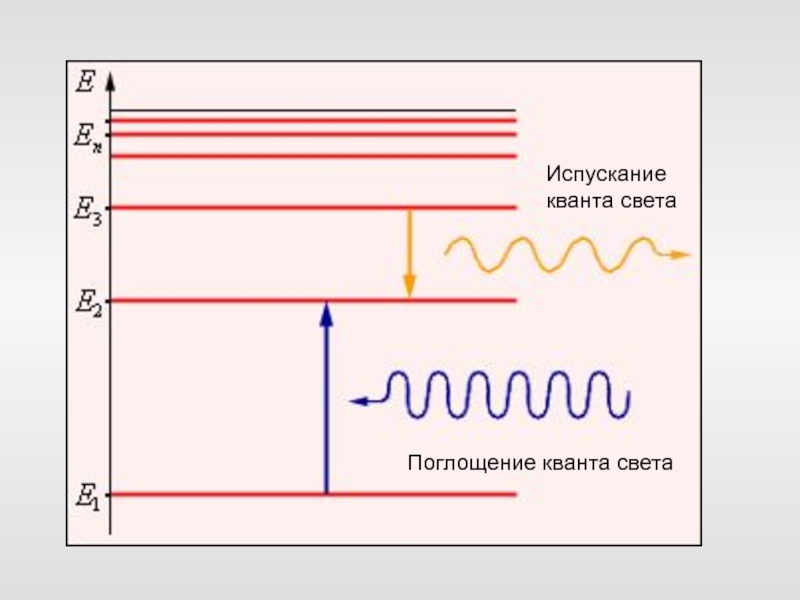
Слайд 32Постулаты Бора
В атоме существуют стационарные состояния, не меняющиеся без внешних
воздействий.
В них атом не излучает энергию.
Энергии стационарных состояний
образуют дискретный спектр
Е1, Е2, Е3 …
Противоречие с классической механикой, где энергия системы может быть любой
Слайд 33Постулаты Бора
При переходе атома из одного стационарного состояния в другое
им испускается или поглощается один квант энергии.
Энергия этого кванта равна разности энергий стационарных состояний:
Противоречие с электродинамикой. Частота волны должна определяться характером движения заряда
Слайд 34Поглощение кванта света
Испускание кванта света
Слайд 36Устойчивость атомов – это макроскопический эффект квантовой механики
В атоме Бора
электроны не падают на ядро
Слайд 37Непоследовательность:
Квантовый принцип противоречил классической механике. Но для расчета орбит использовалась
именно она.
Электродинамика считалась неприменимой (нет излучения)
Недостатки теории Бора
По понедельникам, средам
и пятницам она применяла классические законы, а по вторникам и четвергам – квантовые
Г. Брэгг
Слайд 38Недостатки теории Бора
Квантовый принцип не получил физического объяснения – он
«просто работал и все»
Теория была «полуклассической» и «полуквантовой»
Переходный этап
от классики к квантовой механике
Слайд 39Свет – волна или частица?
Еще одна нерешенная проблема
Максвелл
Планк и Эйнштейн
Слайд 40Второй принцип квантовой механики
Корпускулярно-волновой дуализм
(принцип дополнительности)
Слайд 42Корпускулярно-волновой дуализм
Не только фотоны, но любые тела являются одновременно частицей
и волной
Распространение свойств волны на тела, обладающие массой!
Слайд 43Корпускулярно-волновой дуализм
Длина волны любого тела определяется через импульс
Для тел, имеющих
массу
Из-за малой величины h волновые свойства у тел с большой
массой не проявляются
Слайд 44Как зависит длина волны от импульса
При v
расстояние между атомами в веществе. Из электромагнитных волн такую длину
имеют рентгеновские лучи.
Электрон
Длина волны
Слайд 45Как зависит длина волны от импульса
При v
меньше планковской длины – наименьшей, которую можно теоретически измерить.
Бегущий человек
Длина
волны
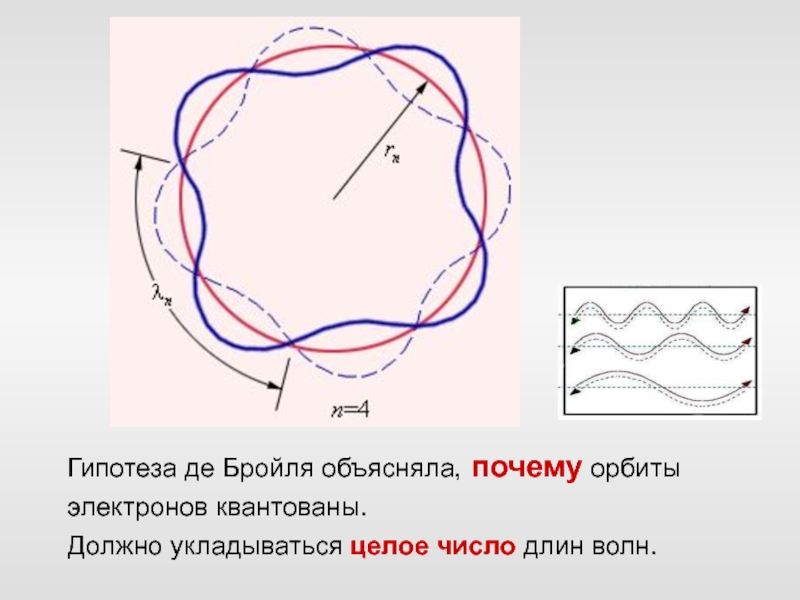
Слайд 46Гипотеза де Бройля объясняла, почему орбиты электронов квантованы.
Должно укладываться
целое число длин волн.
Слайд 47Нильс
Бор
Принцип дополнительности
Принцип соответствия
Слайд 48Принцип дополнительности Бора
Волновое и корпускулярное описание квантового объекта не исключают
и не заменяют, а взаимно дополняют друг друга
Это связано с
тем, что мы вынуждены описывать в классических понятиях объекты, к которым эти понятия неприменимы
Слайд 49Принцип дополнительности в общей формулировке
Многие явления природы не могут быть
определены однозначно с помощью слов нашего языка и требуют для
своего определения, по крайней мере, двух взаимоисключающих дополнительных понятий
Слайд 50Принцип соответствия
Всякая неклассическая теория в соответствующем предельном случае переходит в
классическую
Слайд 51Доказательство волновых свойств частиц, имеющих массу
Дифракция электронов
К.Девиссон и Л. Джермер,
1927
Дж.Томсон, 1928
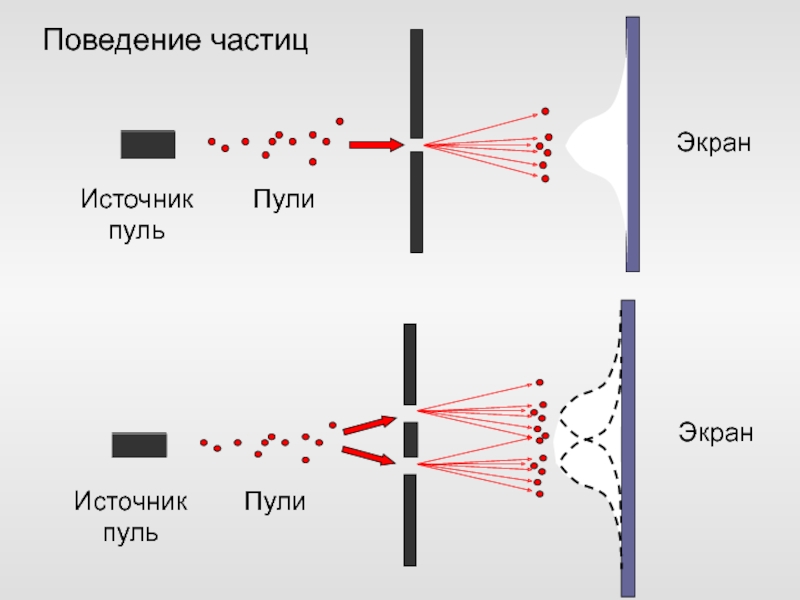
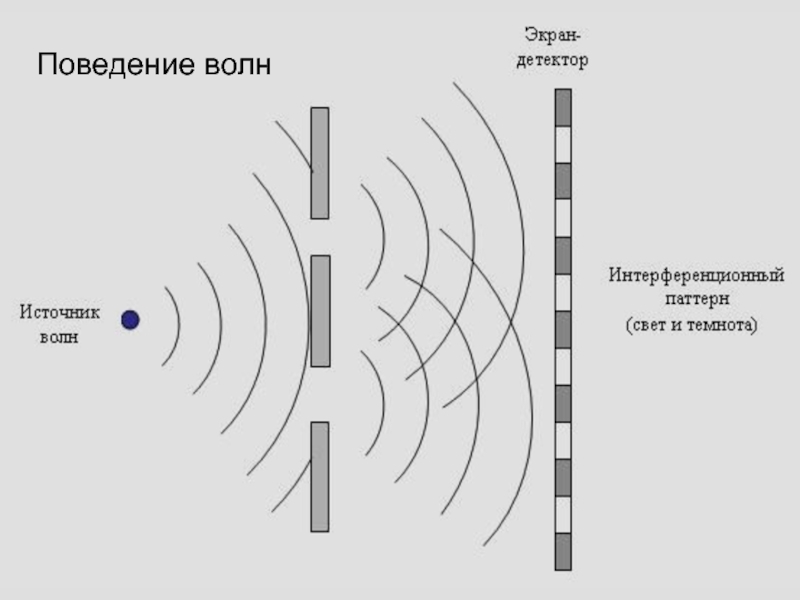
Слайд 52Дифракция – изменение структуры любой волны при огибании препятствий.
Если
за препятствием установить датчик (экран), то на нем появится картинка,
отражающая интенсивность попадающих волн.
Ее называют картиной интерференции – результата взаимодействия всех волн приходящих на экран.
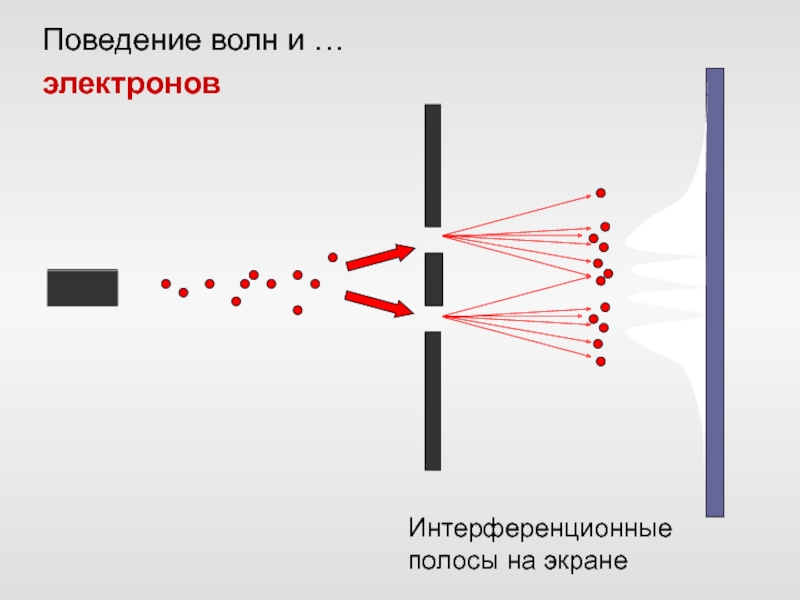
Слайд 55Поведение волн и …
электронов
Интерференционные полосы на экране
Слайд 56Картина дифракции электронов.
В случае (b) видны точки попадания отдельных электронов
(частицы!) на фотопластинку.
Такая картина получается даже если поток электронов
так слаб, что одновременно через перегородку проходит только одна частица.
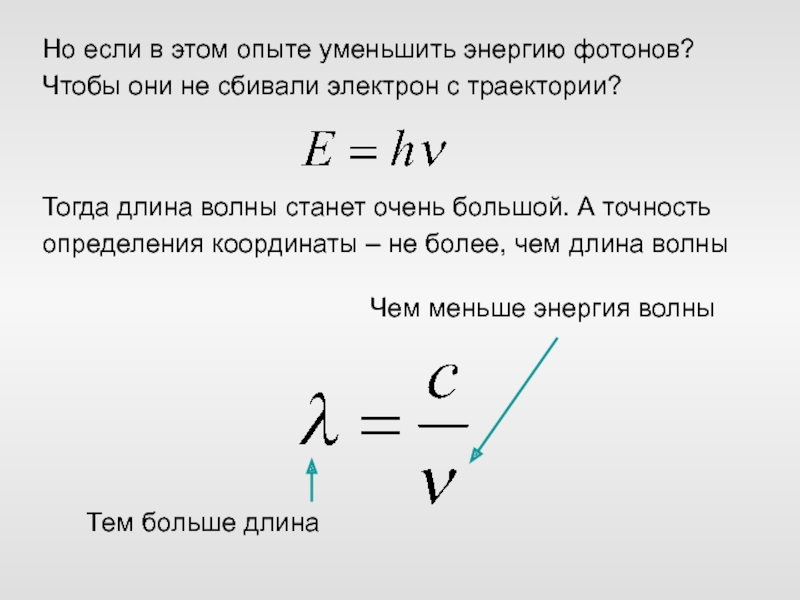
Слайд 58Но если в этом опыте уменьшить энергию фотонов? Чтобы они
не сбивали электрон с траектории?
Тогда длина волны станет очень большой.
А точность определения координаты – не более, чем длина волны
Чем меньше энергия волны
Тем больше длина
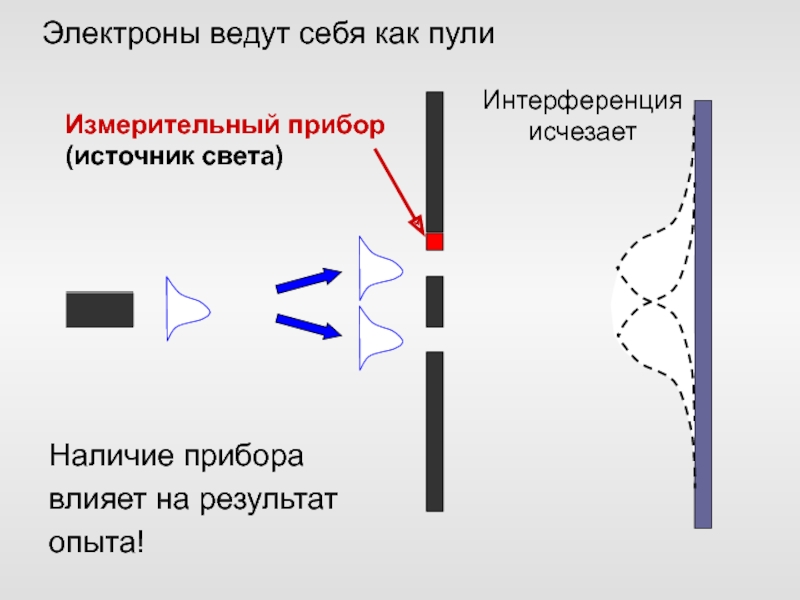
Слайд 60При любых измерениях любыми сверхточными приборами невозможно одновременно точно определить
координату и скорость частицы.
Чем точнее вы измеряете координату – тем
больше будет погрешность в скорости и наоборот:
Соотношение неопределенностей
Δx – погрешность в измерении координаты
Δp – погрешность в измерении импульса
Слайд 61Соотношение неопределенностей
Аналогично для энергии частицы и времени ее измерения
Невозможно сказать,
что частица имеет такую-то энергию в такой-то точный момент времени
Слайд 63Эрвин
Шрёдингер
1928
Нерелятивистская квантовая механика
Слайд 64Квантовый объект – это объект, который не встречается в классической
физике
Поэтому классические понятия в применении к квантовому объекту теряют
свой смысл, но используются за неимением других, а также потому, что квантовый объект является нам всегда в такой ситуации, когда эти понятия имеют (приблизительно) привычный смысл.
В макромире он проявляет себя либо частицей, либо волной, однако теряя при этом часть свойств квантового объекта.
Слайд 65Математический аппарат квантовой механики
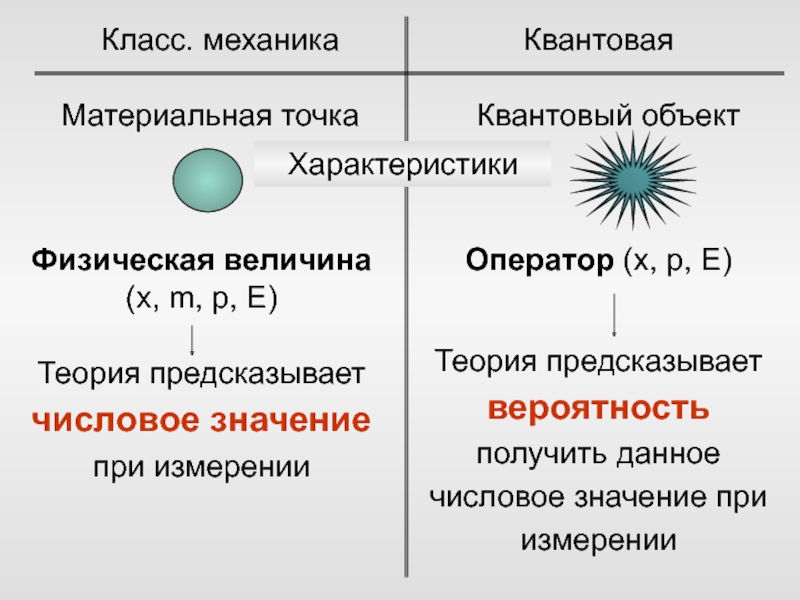
Слайд 66Класс. механика
Квантовая
Физическая величина (x, m, p, E)
Характеристики
Материальная точка
Квантовый объект
Оператор (x,
p, E)
Теория предсказывает числовое значение при измерении
Теория предсказывает вероятность получить
данное числовое значение при измерении
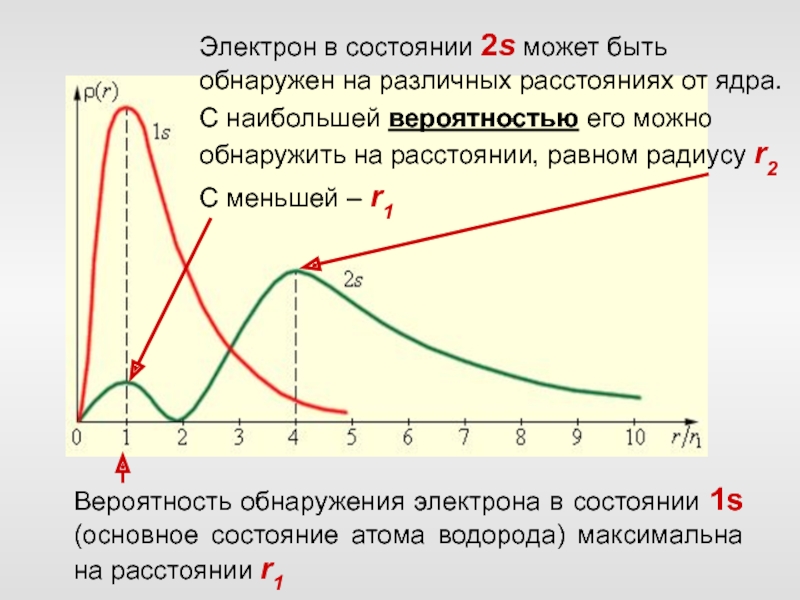
Слайд 67Электрон в состоянии 2s может быть обнаружен на различных расстояниях
от ядра.
С наибольшей вероятностью его можно обнаружить на расстоянии,
равном радиусу r2
С меньшей – r1
Вероятность обнаружения электрона в состоянии 1s (основное состояние атома водорода) максимальна на расстоянии r1
Слайд 68О воспроизводимости в квантовой механике можно говорить лишь в статистическом
смысле, но никогда нельзя предсказать результат одного конкретного измерения
Невыполнимо требование
воспроизводи-мости результатов эксперимента
Дано: 1 000 идентичных физических систем с одинаковой волновой функцией.
Р (r1) = 4/5
Р (r2) = 1/5
в ~800 случаях получим в результате измерения r1,
а в ~200 случаях – r2
Слайд 69Физическая величина для квантового объекта характеризуется не численным значением, а
оператором.
Слайд 70Собственные значения и собственные функции линейных операторов
Если в результате применения
оператора Â к функции u получается та же функция u,
умноженная на некоторое число λ : Â u = λ u ,
то функция u называется собственной функцией оператора Â, принадлежащей собственному значению λ.
В квантовой механике применяются не любые линейные операторы, а лишь самосопряженные, или эрмитовы
Слайд 71Постулаты квантовой механики
Состояние движения частицы описывается волновой функцией Ψ (пси).
Каждая
динамическая переменная представляется определенным линейным эрмитовым оператором.
При измерении числового значения
величины, изображаемой оператором Â, с определенной вероятностью получается одно из чисел а1, а2 .. аn являющихся собственными значениями оператора
Волновая функция Ψ подчиняется ур. Шрёдингера
Слайд 72Уравнение Шрёдингера
для одной частицы
Волновая функция (пси)
– плотность вероятности найти частицу
в объеме dv в момент t
– плотность вероятности найти
в момент t частицу 1 в объеме dv1, частицу 2 – в объеме dv2 и т.д.
Слайд 73Уравнение Шрёдингера
где
– эрмитов оператор, соответствующий гамильтониану системы
Ψ – искомая
волновая функция
постулат
Слайд 74Уравнение Шрёдингера
принцип соответствия Бора
Решениями этого уравнения являются волновые функции
Ψ. Если известна волновая функция Ψ в момент времени t,
то можно получить ее вид в любой последующий момент
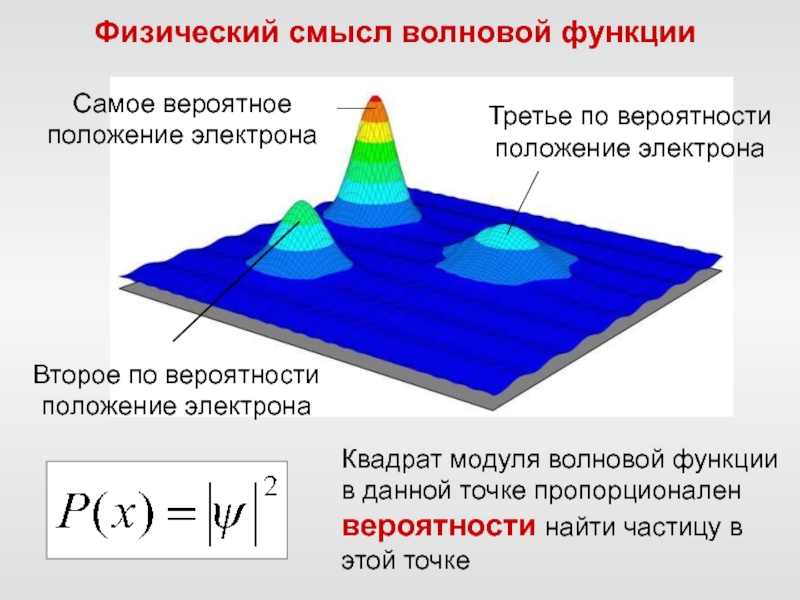
Слайд 75Квадрат модуля волновой функции в данной точке пропорционален вероятности найти
частицу в этой точке
Физический смысл волновой функции
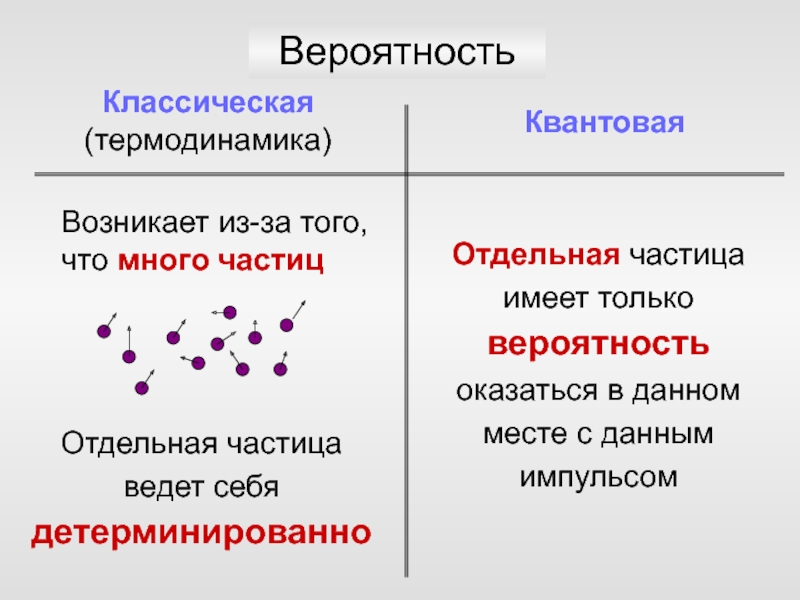
Слайд 76Классическая (термодинамика)
Квантовая
Вероятность
Возникает из-за того, что много частиц
Отдельная частица ведет себя
детерминированно
Отдельная частица имеет только вероятность оказаться в данном месте с
данным импульсом
Слайд 77Источники
В.Е. Фрадкин и В.А. Зверев © 2004 Теория Бора
http://school.iot.ru/predmety/fizika/razrab/teor_bora.ppt
В
лекции использованы отдельные слайды из презентаций
Prof. Bob Cywinski http://www.physics.leeds.ac.uk/graphics/qu4_5.ppt
Слайд 78 Вы можете свободно
Использовать данную презентацию в образовательных целях
с сохранением авторства.
Использовать рисунки и отдельные слайды в своих презентациях
и на сайтах со ссылкой на данный сайт или автора.
Авторские права
Вы НЕ имеете права
Копировать, распространять или использовать ее другим способом для извлечения коммерческой выгоды.
Выкладывать на интернет-сайтах для скачивания.
Использовать слайды, текст и авторские рисунки без ссылок, выдавая их за свои.
© М.А. Волошина 2009
http://biologii.net
Вы скачали данную презентацию с сайта Biologii.Net, согласившись с тем, что
Если вы не согласны с этими условиями, удалите презентацию с вашего компьютера.