Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Квантовые алгоритмы Монте-Карло. Проблема знака Проблема знака. Winding numbers. Связь фермионного знака и winding numbers
Содержание
- 1. Квантовые алгоритмы Монте-Карло. Проблема знака Проблема знака. Winding numbers. Связь фермионного знака и winding numbers
- 2. Проблема знакаВ общем случае для вычисления статистической
- 3. Особенности статистики БозеОсновное отличие – отсутствие запрета
- 4. Особенности при расчете спиновых системДля расчета спиновых
- 5. Winding numbersНедостаток траекторных методов в схеме шахматной
- 6. Связь фермионного знака и winding numbersВ случае
- 7. Связь фермионного знака и winding numbersДалее:Статистический вес:Фермионный
- 8. Связь фермионного знака и winding numbersКонфигурации без разрывов:Число самопересечений траектории:
- 9. Связь фермионного знака и winding numbersФермионный знак
- 10. Связь фермионного знака и winding numbersКонфигурации с несколькими разрывами:Фермионный знак конфигурации:
- 11. Скачать презентанцию
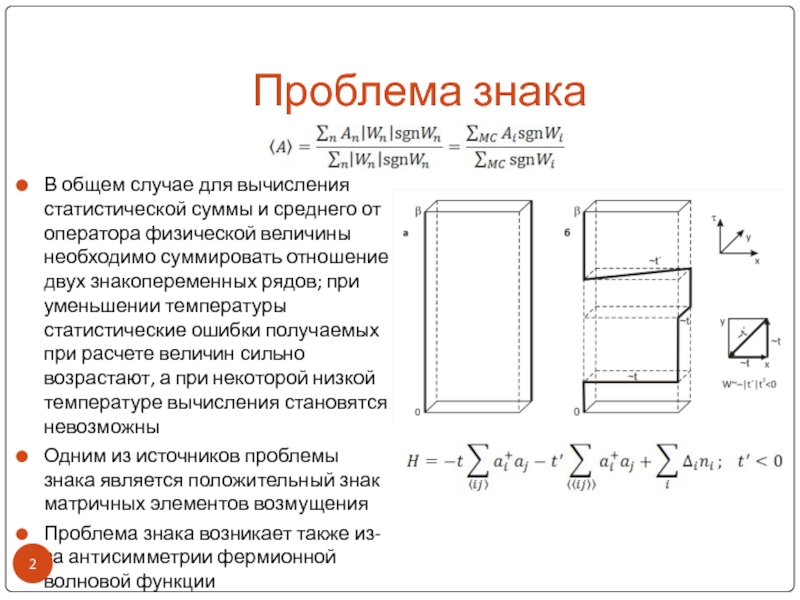
Проблема знакаВ общем случае для вычисления статистической суммы и среднего от оператора физической величины необходимо суммировать отношение двух знакопеременных рядов; при уменьшении температуры статистические ошибки получаемых при расчете величин сильно возрастают,
Слайды и текст этой презентации
Слайд 1Проблема знака.
Winding numbers. Связь фермионного знака и winding numbers
2.12. Квантовые
алгоритмы
Монте-Карло. Проблема знака
Слайд 2Проблема знака
В общем случае для вычисления статистической суммы и среднего
от оператора физической величины необходимо суммировать отношение двух знакопеременных рядов;
при уменьшении температуры статистические ошибки получаемых при расчете величин сильно возрастают, а при некоторой низкой температуре вычисления становятся невозможныОдним из источников проблемы знака является положительный знак матричных элементов возмущения
Проблема знака возникает также из-за антисимметрии фермионной волновой функции
Слайд 3Особенности статистики Бозе
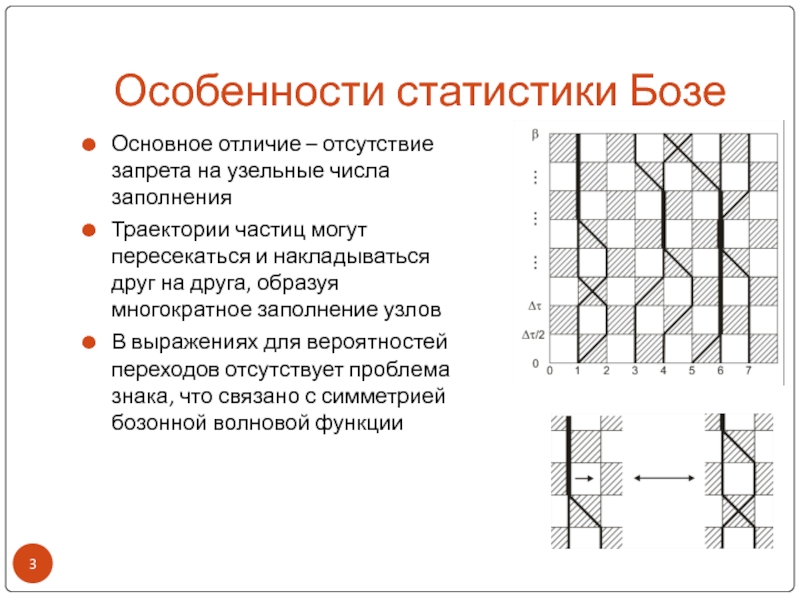
Основное отличие – отсутствие запрета на узельные числа
заполнения
Траектории частиц могут пересекаться и накладываться друг на друга,
образуя многократное заполнение узловВ выражениях для вероятностей переходов отсутствует проблема знака, что связано с симметрией бозонной волновой функции
Слайд 4Особенности при расчете
спиновых систем
Для расчета спиновых систем удобно перейти к
неотрицательным числам заполнения – к фиктивным бозонам
XXZ-модель Гейзенберга с анизотропным
по одному из направлений взаимодействием:Проблема знака для спиновых моделей Гейзенберга связана со знаком обменного интеграла при поперечной компоненте взаимодействия. Однако фундаментальные свойства основного состояния определяет параллельная компонента взаимодействия, матричные элементы которой диагональны
Слайд 5Winding numbers
Недостаток траекторных методов в схеме шахматной доски: число оборотов
траектории частицы по координатной или временной оси – winding numbers
– всегда остается фиксированнымКонфигурации с ненулевыми winding numbers также имеют ненулевой вес
Выражения для сверхтекучей плотности связано с квадратичной флуктуацией числа закруток
Слайд 6Связь фермионного знака
и winding numbers
В случае системы фермионов статистический вес
любой системы траекторий, помимо знака, связанного со знаком матричных элементов
возмущения, имеет дополнительный знак, возникающий из-за антисимметрии волновой функции фермионов относительно перестановок частицАнтисимметрия волновых функций и тождественность частиц в ферми-системах являются причиной стандартного антикоммутационного соотношения в представлении вторичного квантования:
При сквозной нумерации узлов в системе это приводит к известному выражению для матричных элементов операторов рождения и уничтожения:
Слайд 7Связь фермионного знака
и winding numbers
Далее:
Статистический вес:
Фермионный знак совершенно не зависит
от нумерации узлов и отражает исключительно топологию системы мировых линий
Полученные
результаты будут справедливы и для квантовых методов МК в непрерывном времени
Слайд 8Связь фермионного знака
и winding numbers
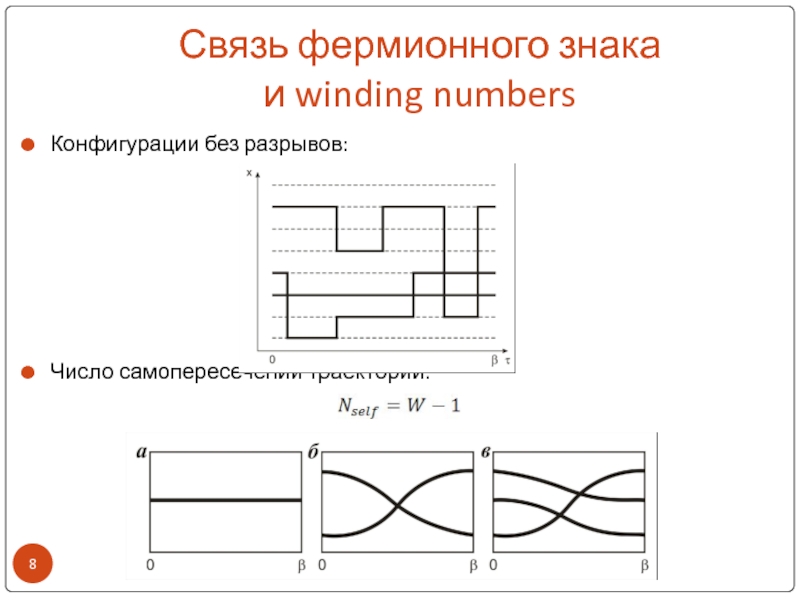
Конфигурации без разрывов:
Число самопересечений траектории:
Слайд 9Связь фермионного знака
и winding numbers
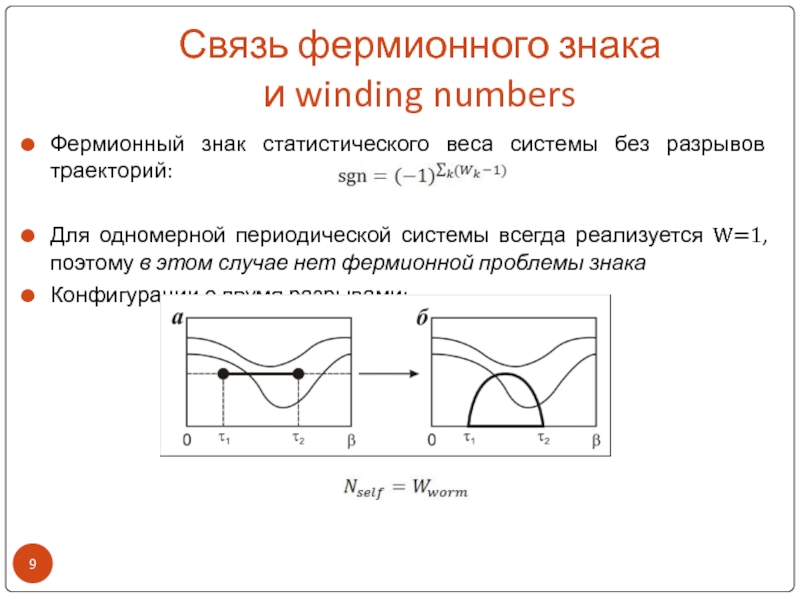
Фермионный знак статистического веса системы без
разрывов траекторий:
Для одномерной периодической системы всегда реализуется W=1, поэтому в
этом случае нет фермионной проблемы знакаКонфигурации с двумя разрывами: