Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Квантовые состояния многоэлектронных атомов. Правило Хунда.
Содержание
- 1. Квантовые состояния многоэлектронных атомов. Правило Хунда.
- 2. Рассмотрим более сложные примеры.Пусть один из электронов
- 3. Рассмотрим случай l2 = 1 (оба электрона
- 4. Если S = 1, то количество
- 5. Итак, двум p-электронам отвечает де-сять возможных состояний
- 6. Действительно, при данных L и S воз-можные
- 7. Составим таблицу возможных значений ML для двух
- 8. Оставшиеся значения ML можно разбить на две
- 9. Если ms1 = ms2, т.е. если S=1,то
- 10. Аналогичные рассуждения можно про-вести для любого количества
- 11. Правило ХундаСреди термов, принадлежащих одной элект-ронной конфигурации,
- 12. Правило Хунда является следствием взаимного отталкивания электронов.
- 13. В качестве примера рассмотрим атом, который имеет
- 14. Скачать презентанцию
Рассмотрим более сложные примеры.Пусть один из электронов перешел в сос-тояние l1 = 1, а второй может оказаться в состояниях l2 = 0, 1, 2. Запишем воз-можные значения L в виде таблицы:
Слайды и текст этой презентации
Слайд 1Физика атома, атомного ядра и элементарных частиц
19 (2). Квантовые состояния
многоэлектронных атомов. Правило Хунда.
Слайд 2Рассмотрим более сложные примеры.
Пусть один из электронов перешел в сос-тояние
l1 = 1, а второй может оказаться в состояниях l2
= 0, 1, 2. Запишем воз-можные значения L в виде таблицы:Слайд 3Рассмотрим случай l2 = 1 (оба электрона в состоянии p).
Тогда L=0, 1, 2.
Если S = 0, то J =
L, и возможны состояния:при ,
при ,
при .
Слайд 4
Если S = 1, то количество термов будет больше,
т.к. тогда J = L+1, L, L-1.
Если L=0, то
.Если L = 1, то возможно
Если L = 2, то возможно
Слайд 5Итак, двум p-электронам отвечает де-сять возможных состояний атома. Од-нако все
они могут осуществиться толь-ко в том случае, если не нарушен
прин-цип Паули. Если n1 и n2 (главные кван-товые числа) различны, то могут осу-ществиться все десять возможных сос-тояний. Если же n1 = n2, то некоторые из найденных термов оказываются за-прещенными принципом Паули.Слайд 6Действительно, при данных L и S воз-можные значения магнитных кван-товых
чисел ML и MS определяются условиями:
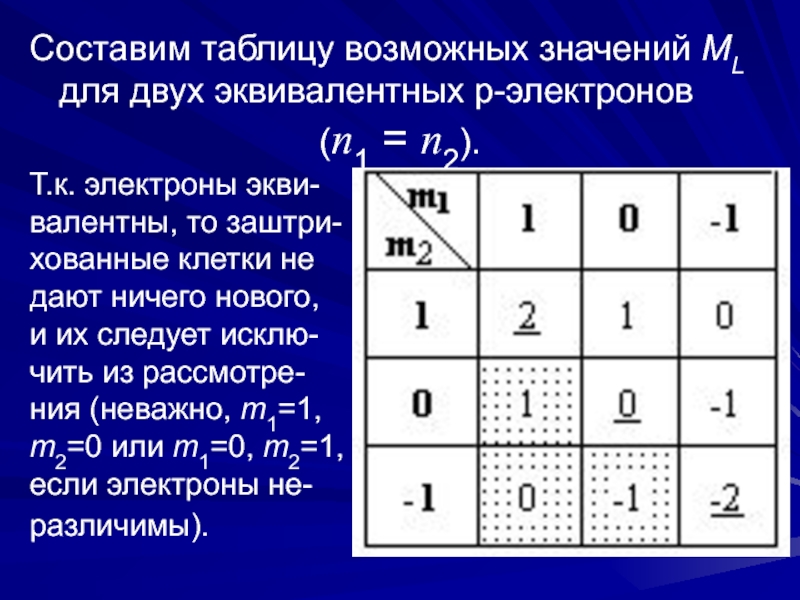
Слайд 7Составим таблицу возможных значений ML для двух эквивалентных p-электронов
(n1 =
n2).
Т.к. электроны экви-
валентны, то заштри-
хованные клетки не
дают ничего нового,
и их
следует исклю-чить из рассмотре-
ния (неважно, m1=1,
m2=0 или m1=0, m2=1,
если электроны не-
различимы).
Слайд 8Оставшиеся значения ML можно разбить на две группы:
Эти значения
осуществляются, если m1=m2, это возможно, если ms1 ≠ ms2, т.е.
если S=0. Поэтому в системе синглетных сос-тояний (S = 0, κ = 1) остаются состояния 1S0 и 1D2 (исключено состояние 1P1).
Слайд 9Если ms1 = ms2, т.е. если S=1,
то невозможны состояния с
m1=m2,
поэтому значения ML
на главной диагонали (под-
черкнуты) следует отбросить.
Тогда остается только
одинряд значений ML:
Поэтому в системе триплетных состояний оста-ются состояния .
Итак, в случае двух эквивалентных p-электронов возможно существование только пяти состоя-ний (вместо десяти для электронов с n1 ≠ n2).
Слайд 10Аналогичные рассуждения можно про-вести для любого количества электро-нов, причем векторная
модель очень точно предсказывает особенности спектров сложных атомов.
После того, как
найдены возможные тер-мы атомов, возникает вопрос, какой из этих термов основной. На этот вопрос дает ответ правило, эмпирически уста-новленное в 1926г Фридрихом Хундом (Hund F.)Слайд 11Правило Хунда
Среди термов, принадлежащих одной элект-ронной конфигурации, самым глубоким яв-ляется
тот, который связан с наибольшим значением S, а среди термов
с равным S – тот, который связан с наибольшим L. При этом для основного терма , если оболочка заполнена менее, чем наполови-ну, и в остальных случаях. Други-ми словами, электроны в атоме стремятся (когда это не противоречит принципу Пау-ли) оставаться не спаренными, т.е. иметь параллельные спины (при этом S будет наибольшим).
Слайд 12Правило Хунда является следствием взаимного отталкивания электронов. Действительно, энер-гия атома
(с учетом взаимодействия между электронами) тем меньше, чем дальше друг
от друга находятся электроны. Если электроны имеют одинаковые n, l и ms (спины параллель-ны), то они должны иметь различные m, т.е. волновые функции с различными пространст-венными распределениями (“двигаться по раз-ным орбитам”, говоря на языке теории Бора), поэтому такие электроны отстоят в атоме даль-ше друг от друга (в среднем), чем спаренные (с антипараллельными спинами); следовательно, в таком состоянии атом обладает меньшей энергией, т.е. терм находится ниже.Слайд 13В качестве примера рассмотрим атом, который
имеет два валентных p
– электрона. Это может
быть, например, атом углерода
илиатом кремния . Такой атом, как
мы только что установили, может находиться в
состояниях: 1S0 , 1D2 , . Какое из них
основное? Согласно правилу Хунда основным бу-
дет состояние, соответствующее S = 1, т.е. один
из P-термов. Т.к. оболочка 2p2 заполнена менее,
чем наполовину, то . Таким образом,
основной терм атома углерода и кремния 3P0.