Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Ламинарное и турбулентное течение
Содержание
- 1. Ламинарное и турбулентное течение
- 2. Скорость течения крови значительно различается в разных
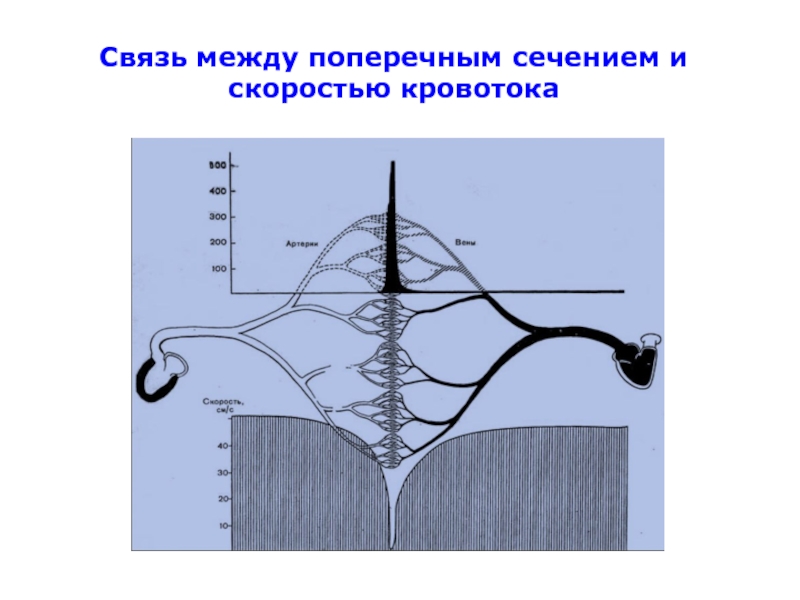
- 3. Связь между поперечным сечением и скоростью кровотока
- 4. Уравнение БернуллиЗакон Бернулли является следствием закона сохранения
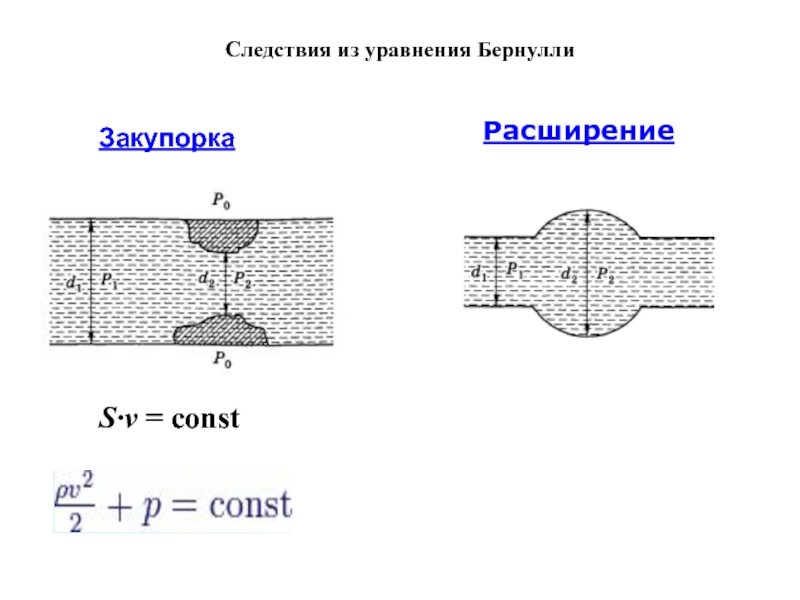
- 5. Следствия из уравнения БернуллиЗакупоркаРасширениеS·v = const
- 6. Внутреннее трение (вязкость жидкости). Уравнение Ньютона
- 7. Ньютоновские и неньютоновские жидкостиσ=η ∙ grad νη
- 8. Формула ПуазейляЖан Мари Пуазейль(1799-1869)Французский врач, физик, физиолог,
- 9. Характер течения жидкости определяется числом РейнольдсаРЕЙНОЛЬДС, ОСБОРН
- 10. Кровь относится к неньютоновским жидкостям. Ее вязкость
- 11. Слайд 11
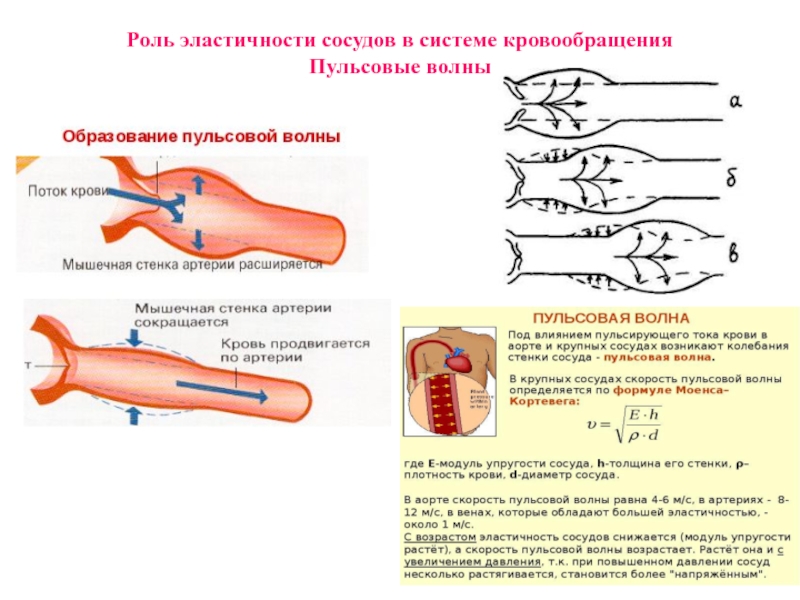
- 12. Роль эластичности сосудов в системе кровообращения Пульсовые волны
- 13. Скачать презентанцию
Скорость течения крови значительно различается в разных отделах кровеносной системы. Она определяется уравнением неразрывности потока.S·v = constЧерез каждый уровень поперечного сечения, обозначенный вертикальными линиями, протекает одинаковый объем кровиПлощадь поперечного сечения аорты
Слайды и текст этой презентации
Слайд 1Ламинарное и турбулентное течение
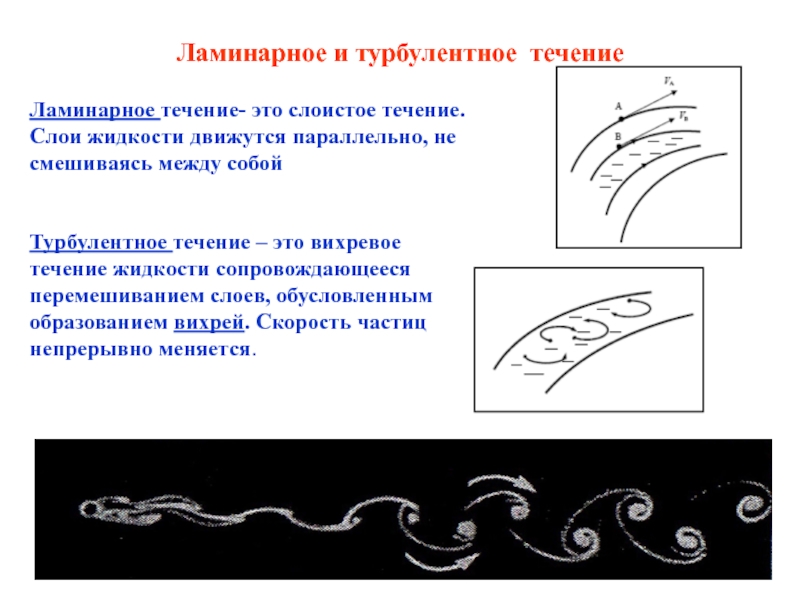
Ламинарное течение- это слоистое течение.
Слои жидкости движутся
параллельно, не смешиваясь между собой
течение жидкости сопровождающееся перемешиванием слоев, обусловленным образованием вихрей. Скорость частиц непрерывно меняется.
Слайд 2Скорость течения крови значительно различается в разных отделах кровеносной системы.
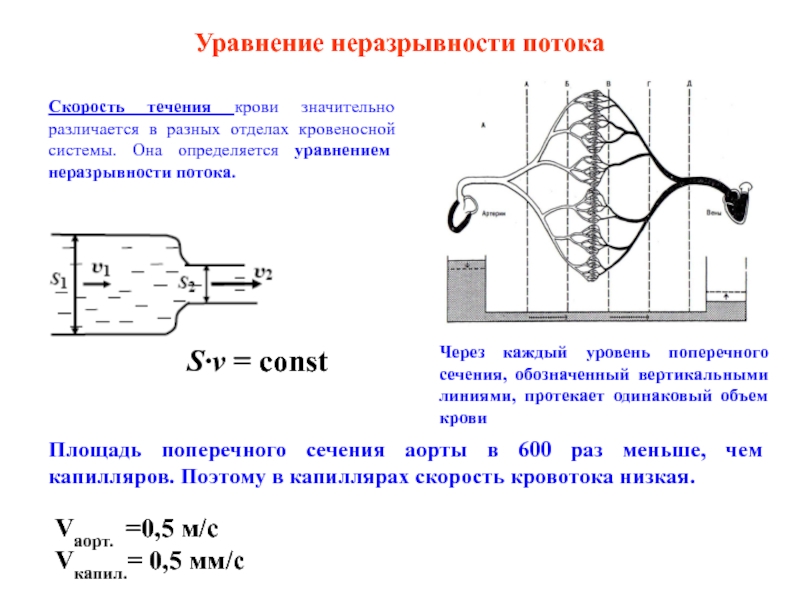
Она определяется уравнением неразрывности потока.
S·v = const
Через каждый уровень поперечного
сечения, обозначенный вертикальными линиями, протекает одинаковый объем кровиПлощадь поперечного сечения аорты в 600 раз меньше, чем капилляров. Поэтому в капиллярах скорость кровотока низкая.
Vаорт. =0,5 м/с
Vкапил.= 0,5 мм/с
Уравнение неразрывности потока
Слайд 4Уравнение Бернулли
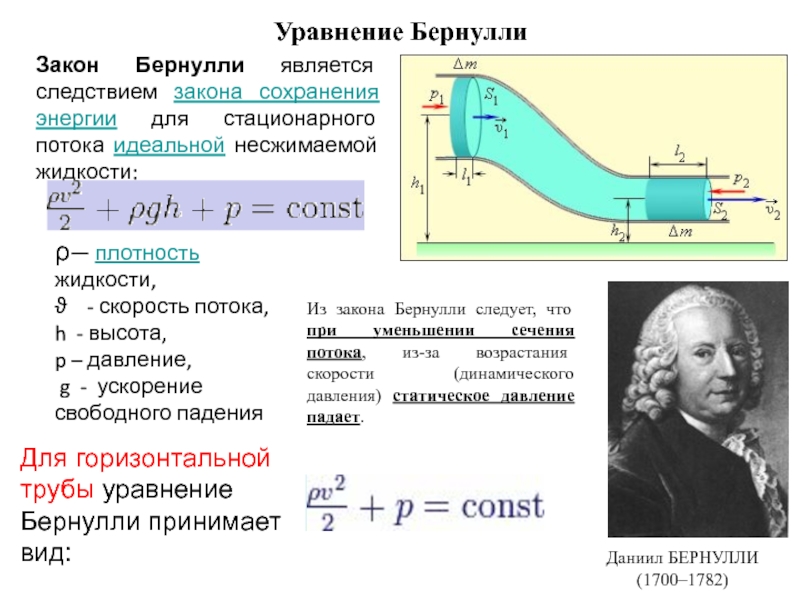
Закон Бернулли является следствием закона сохранения энергии для стационарного
потока идеальной несжимаемой жидкости:
ρ— плотность жидкости,
ϑ - скорость потока,
h
- высота,p – давление,
g - ускорение свободного падения
Для горизонтальной трубы уравнение Бернулли принимает вид:
Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости (динамического давления) статическое давление падает.
Даниил БЕРНУЛЛИ
(1700–1782)
Слайд 6Внутреннее трение (вязкость жидкости).
Уравнение Ньютона
Вязкость (внутреннее трение) – это
свойство текучих тел оказывать сопротивление перемещению одной их части относительно
другойОсновной закон вязкого течения был установлен Ньютоном (1713)
Формулировка: сила внутреннего трения F между слоями движущейся жидкости прямо пропорциональна скорости сдвига и площади поверхности соприкасающихся слоев S. Коэффициентом пропорциональности является коэффициент вязкости η.
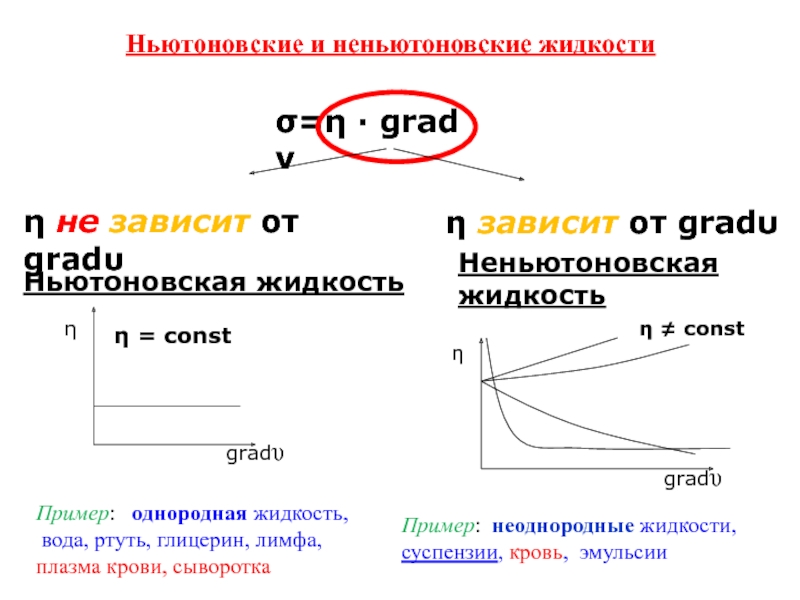
Слайд 7Ньютоновские и неньютоновские жидкости
σ=η ∙ grad ν
η не зависит от
gradυ
η зависит от gradυ
Ньютоновская жидкость
Неньютоновская жидкость
η = const
η
gradυ
η ≠ const
η
gradυ
Пример:
однородная жидкость,вода, ртуть, глицерин, лимфа,
плазма крови, сыворотка
Пример: неоднородные жидкости, суспензии, кровь, эмульсии
Слайд 8Формула Пуазейля
Жан Мари Пуазейль
(1799-1869)
Французский врач, физик, физиолог, преподавал медицинскую физику
Формулировка: Объём жидкости Q, протекающей по горизонтальной трубе небольшого сечения
за единицу времени, прямо пропорционален радиусу трубы R в четвёртой степени, разности давлений ∆P на концах трубы, обратно пропорционален коэффициенту вязкости η и длине трубы. Коэффициентом пропорциональности является π/8 (получен эмпирически).
Слайд 9Характер течения жидкости определяется числом Рейнольдса
РЕЙНОЛЬДС, ОСБОРН
(1842–1912),
английский
инженер и физик
В 1883 Рейнольдс установил, что ламинарное течение переходит
в турбулентное, когда введенное им число Рейнольдса превышает критическое значение. Если Re < Reкр => Ламинарное течение
Если Re > Reкр = > Турбулентное течение
Величина безразмерная
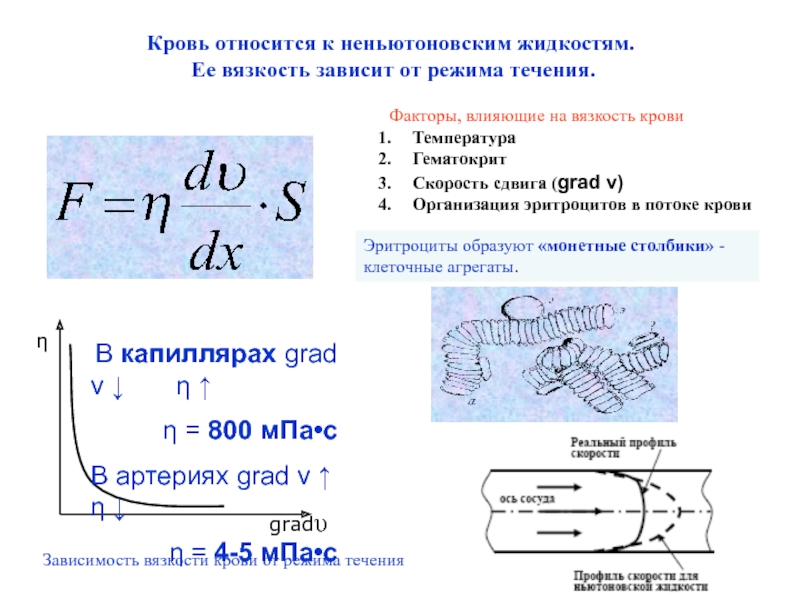
Слайд 10Кровь относится к неньютоновским жидкостям.
Ее вязкость зависит от режима
течения.
η
gradυ
В капиллярах grad v ↓ η
↑η = 800 мПа•с
В артериях grad v ↑ η ↓
η = 4-5 мПа•с
Зависимость вязкости крови от режима течения
Факторы, влияющие на вязкость крови
Температура
Гематокрит
Скорость сдвига (grad ν)
Организация эритроцитов в потоке крови
Эритроциты образуют «монетные столбики» - клеточные агрегаты.
