ЛЕКЦИЯ-ЛОГИКА.ppt

Содержание

1. ЛЕКЦИЯ-ЛОГИКА.ppt
2. Элементы логики
3. ЛогикаЛогика - это наука, изучающая методы доказательств
4. Логическая функция Логическая функция –
5. Основные подходы к:Установление истинности высказыванийэмпирическийлогическийС помощью некоторых проверяющих действийНа основе истинности других высказываний,чисто формально, с помощьюрассуждений.
6. Основные логические связки
7. Инверсия (НЕ)⎤А = 1-А«не А»Отрицание истинно, если ложно исходное утверждение.Отрицание ложно, если исходное утверждение истинно.L
8. Конъюнкция (И)А И В = а *
9. Дизъюнкция (ИЛИ)А ∨ В = a +
10. Импликация (ЕСЛИ … ТО)А →В = ⎤А
11. Эквивалентность (ЕСЛИ И ТОЛЬКО ЕСЛИ)А ~
12. Неравнозначность (ЛИБО…ЛИБО) А ⊕ В =⎤А ИЛИ
13. Аксиомы (1,2) Утверждает, что в алгебре
14. Аксиомы (3,4,5)Определяютоперации конъюнкции и дизъюнкции1 v 1
15. Принцип двойственности Если в аксиомах 2
16. Упражнение : Какие выражения являются истинными, а какие - ложными?х2>0x2
17. Упражнение :Приведите отрицания к утверждениям: На улице
18. Логическая функция
19. Формула алгебры высказываний определяется следующим образом: 1.
20. Примеры формул
21. Таблица истинности Табличное задание функции алгебрылогики
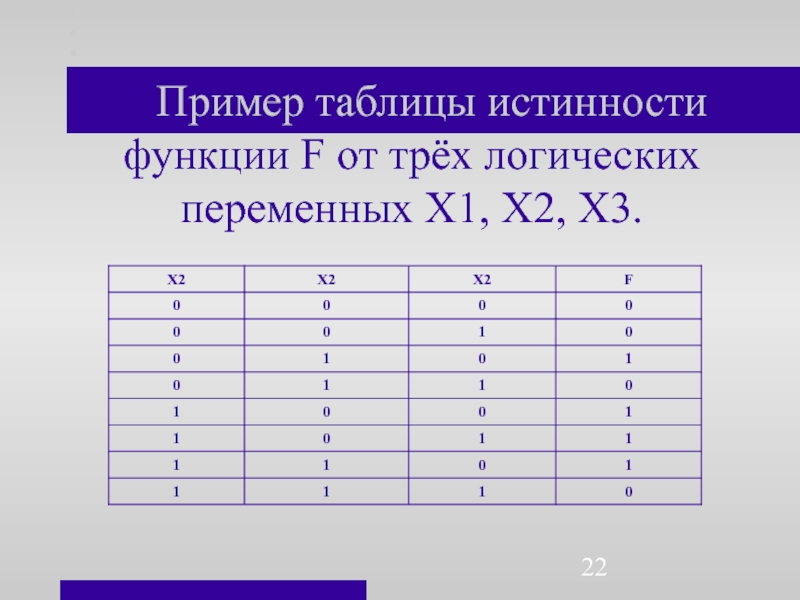
22. Пример таблицы истинности функции F от трёх логических переменных X1, X2, X3.
23. Отметим, что
24. Для любого выражения можнопроверить
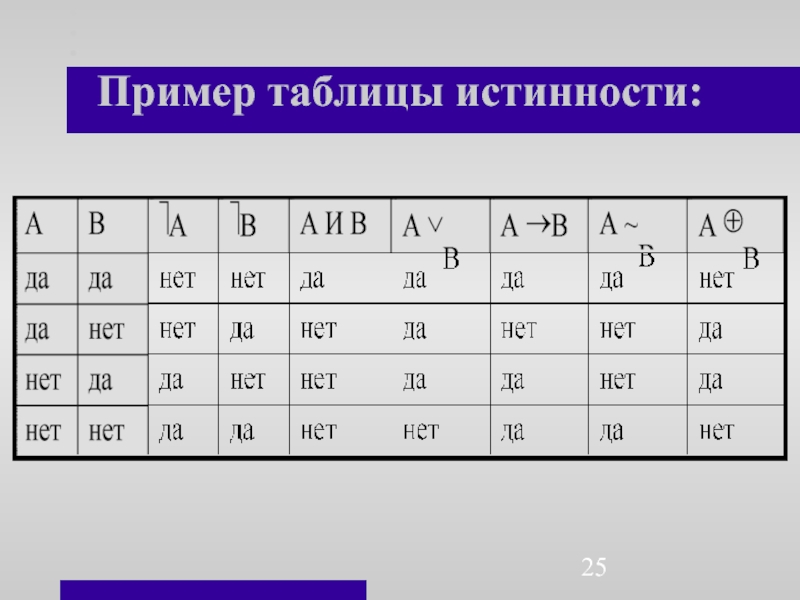
25. Пример таблицы истинности:
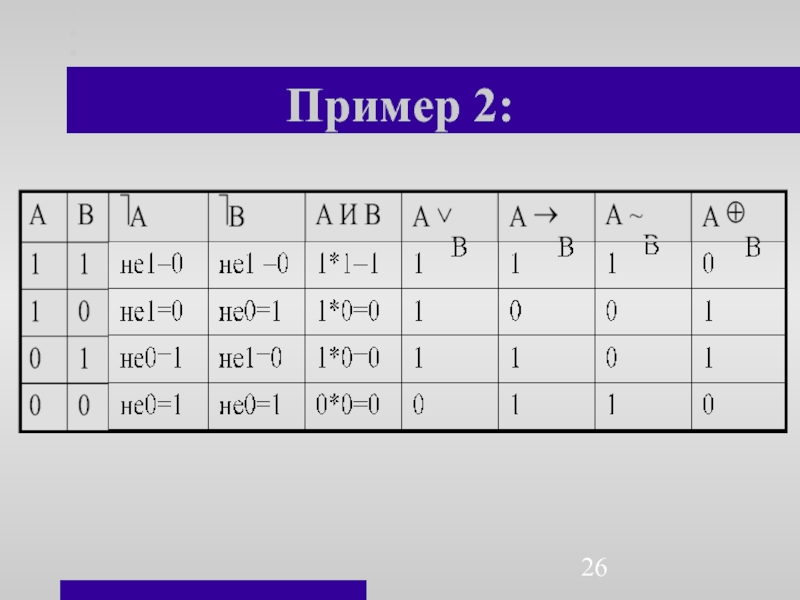
26. Пример 2:
27. Для этого необходимо формулу
28. Например: При построении таблицы истинности
29. F(X1, X2, X3)= ⎤ (⎤ (X2 ∨ X3) ∨ ⎤ X1)
30. Правило отрицания обратной истинности: ⎤ (A ^
31. Правило отрицания обратной истинности:
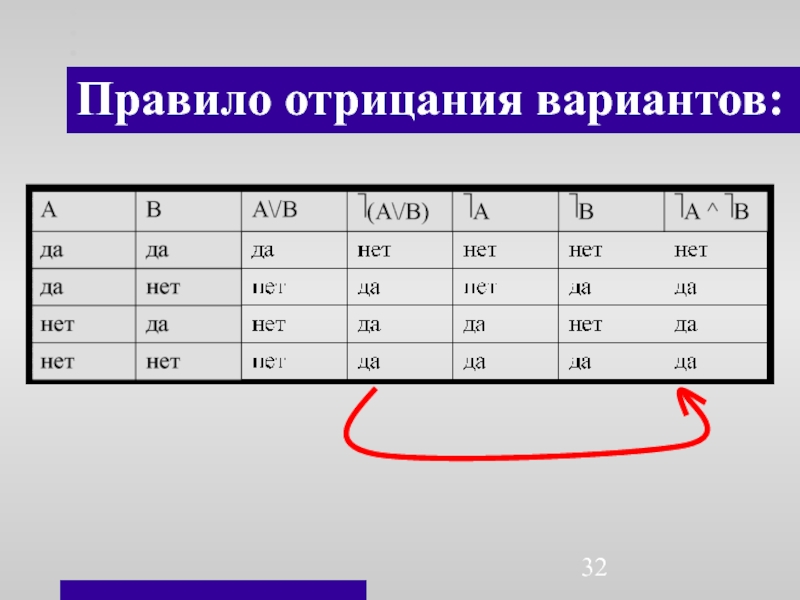
32. Правило отрицания вариантов:
33. Упражнение:Построить таблицы истинности:А^⎤A⎤ (A→B)A^(A→B)А\/⎤AA→⎤B⎤A→⎤B
34. Упражнение: Построить отрицание высказываний:(⎤A)(A^B^C)⎤( ⎤( ⎤A))(A\/B\/C)
35. Обратная задача:по таблице истинности булевой функции следует
36. Элементарная конъюнкция Элементарной конъюнкцией называется логическое
37. Дизъюнктивная нормальная форма Дизъюнктивной нормальнойформой
38. Совершенная дизъюнктивная нормальная форма Совершенной
39. Примеры: 1. Формула ⎤X1 & X2
40. Свойство элементарной конъюнкции: Длина
41. Например,набору (0,1,0) соответствует конъюнкция ⎤X1 &
42. Если подформулу F1 формулы
43. Примеры пар равносильных формул:А∨В и В∨А ;
44. Проверка равносильности: Наиболее просто
45. Основы алгоритмизации
46. Определение алгоритмаАлгоритм решения задачи – система точно
47. Свойства алгоритма: Определенность(точность) Результативность Массовость
48. Способы описания СловесныйФормульно-словесныйСхемныйЯзык операторных схемЯзыки программирования
49. Схема определения алгоритмаВсякий алгоритм применяется к исходным
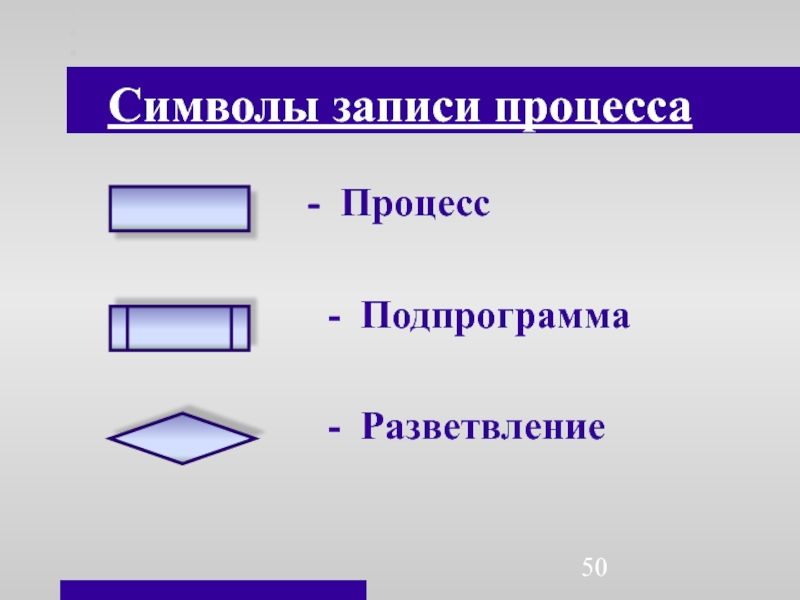
50. Символы записи процесса
51. Символы записи процесса (2)
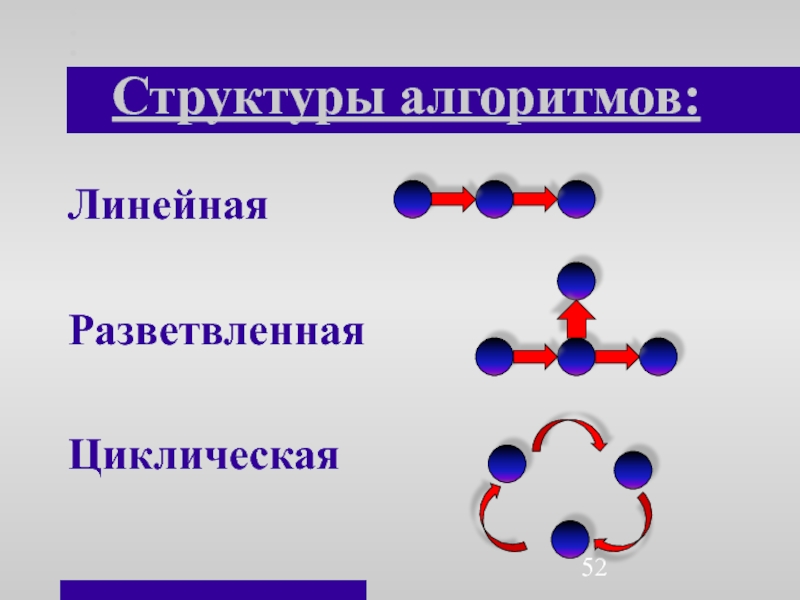
52. Структуры алгоритмов:ЛинейнаяРазветвленнаяЦиклическая
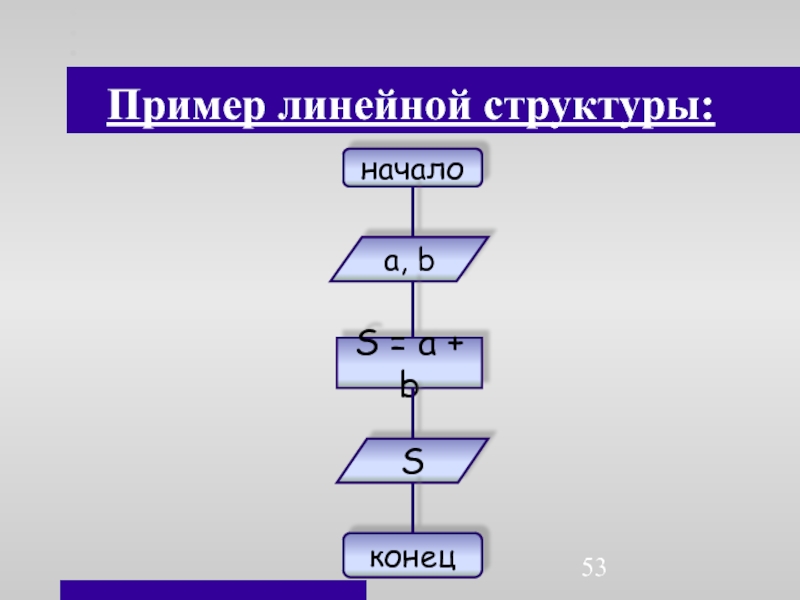
53. Пример линейной структуры:началоа, bS = a + bSконец
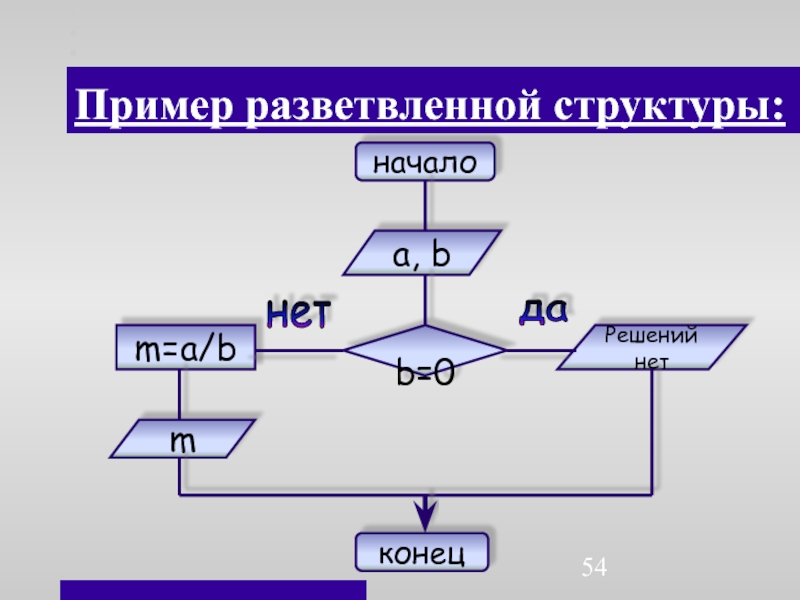
54. Пример разветвленной структуры:началоа, b b=0Решений нетm=a/bmконецданет
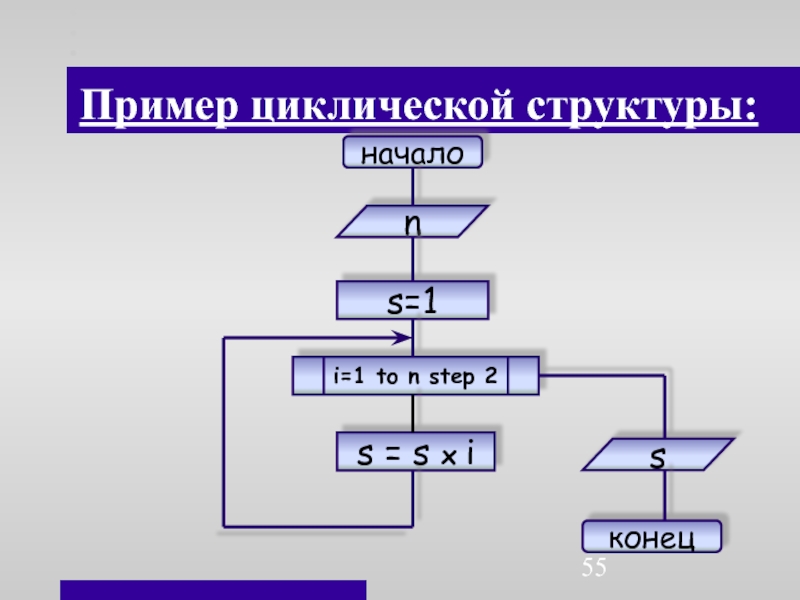
55. Пример циклической структуры:началоi=1 to n step 2s = s x ins=1sконец
56. Пример алгоритма: Является ли натуральное число,
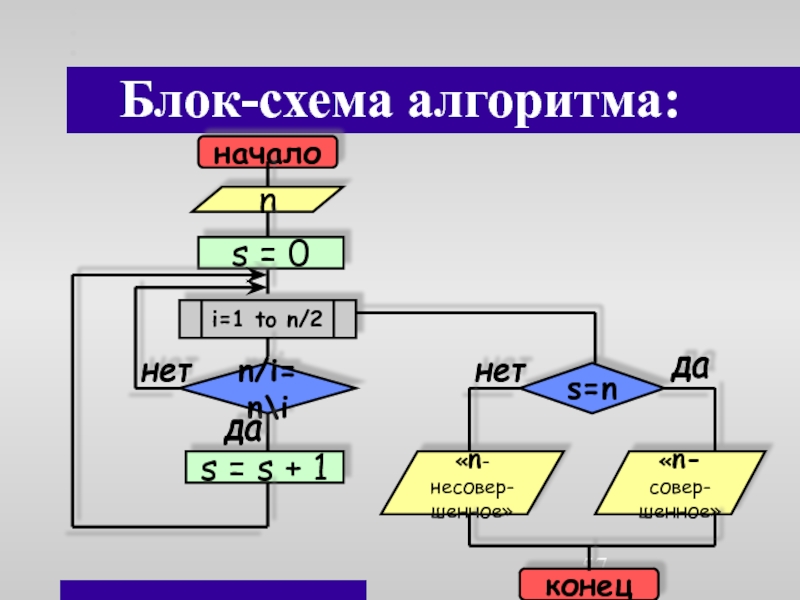
57. Блок-схема алгоритма:началоns = 0i=1 to n/2n/i=n\is = s + 1s=n«n-несовер-шенное»«n- совер-шенное»конецдаданетнет
58. Успехов в познании!!!
59. Скачать презентанцию

Элементы логики

Слайды и текст этой презентации

Слайд 1Введение в алгебру логики. Основы алгоритмизации.

Слайд 2Элементы логики

Слайд 3Логика
Логика - это наука, изучающая методы доказательств и опровержений –

методы установления истинности или ложности одних высказываний (утверждений) на основе

истинности или ложности других высказываний.

ЛогикаЛогика - это наука, изучающая методы доказательств и опровержений – методы установления истинности или ложности одних высказываний

Слайд 4Логическая функция
Логическая функция –
это

алгебраическое выражение, содержащие элементы алгебры логики, связанные между собой операциями,

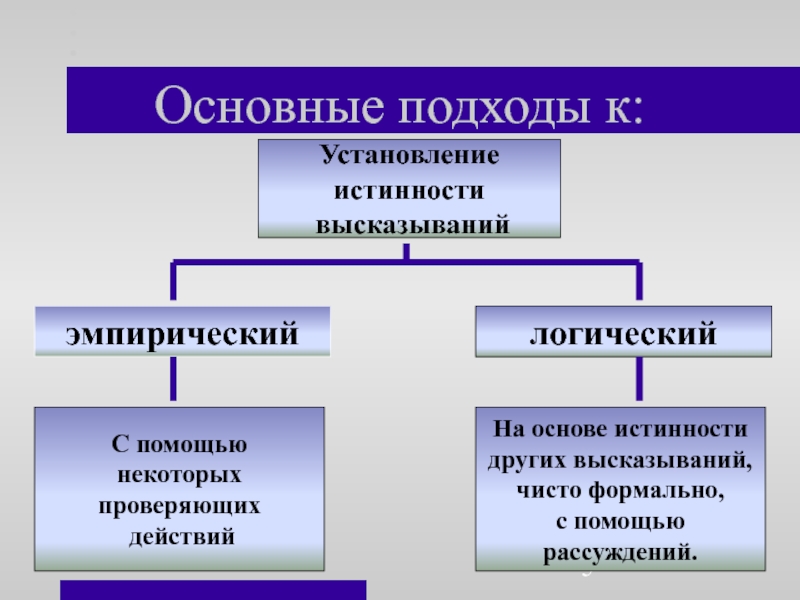
определенными в этой алгебре.

Логическая функция Логическая функция – это алгебраическое выражение, содержащие элементы алгебры логики, связанные между

Слайд 5Основные подходы к:
Установление
истинности
высказываний
эмпирический
логический
С помощью
некоторых
проверяющих
действий
На основе

истинности
других высказываний,
чисто формально,
с помощью
рассуждений.

Основные подходы к:Установление истинности высказыванийэмпирическийлогическийС помощью некоторых проверяющих действийНа основе истинности других высказываний,чисто формально, с помощьюрассуждений.

Слайд 6 Основные логические связки

Слайд 7Инверсия (НЕ)
⎤А = 1-А
«не А»
Отрицание истинно, если ложно исходное утверждение.
Отрицание

ложно, если исходное утверждение истинно.
L

Слайд 8Конъюнкция (И)
А И В = а * b
«А и В»
Красивые

и умные – однозначная истинность составляющих суждений.
Выражение истинно, если истинны

все его составляющие.
Выражение считается ложным, если ложно ходя бы одно из его составляющих.

Конъюнкция (И)А И В = а * b«А и В»Красивые и умные – однозначная истинность составляющих суждений.Выражение

Слайд 9Дизъюнкция (ИЛИ)
А ∨ В = a + b – a*b
«А

или В»
Составное суждение со связкой ИЛИ считается истинным, если истинно

хотя бы одно из составляющих суждений и считается ложным, если ложны все его составляющие.

Дизъюнкция (ИЛИ)А ∨ В = a + b – a*b«А или В»Составное суждение со связкой ИЛИ считается

Слайд 10Импликация (ЕСЛИ … ТО)
А →В = ⎤А И В =

⎤а * б
«А влечет В»
Высказывание ложно только в том

случае, если ложно первое из его составляющих.

[

Импликация (ЕСЛИ … ТО)А →В = ⎤А И В = ⎤а * б «А влечет В»Высказывание ложно

Слайд 11Эквивалентность (ЕСЛИ И ТОЛЬКО ЕСЛИ)

А ~ В
«А, если и

только если В»
Высказывание истинно, если А = В.
Высказывание ложно

, если А ≠ B.

Эквивалентность (ЕСЛИ И ТОЛЬКО ЕСЛИ)А ~ В «А, если и только если В» Высказывание истинно, если

Слайд 12Неравнозначность (ЛИБО…ЛИБО)

А ⊕ В =⎤А ИЛИ В = (1-a) + b

– (1-a) * b
«либо А либо В »
Высказывание истинно, когда

А ≠ В
Высказывание ложно, когда А = В

Неравнозначность (ЛИБО…ЛИБО) А ⊕ В =⎤А ИЛИ В = (1-a) + b – (1-a) * b«либо А

Слайд 13Аксиомы (1,2)
Утверждает, что в алгебре логики рассматриваются

только двоичные переменные

Определяет операцию отрицания
x = 0, если x –

1

x = 1, если x - 0

⎤0 = 1

⎤1 = 0

Аксиомы (1,2) Утверждает, что в алгебре логики рассматриваются только двоичные переменныеОпределяет операцию отрицанияx = 0,

Слайд 14Аксиомы (3,4,5)

Определяют
операции
конъюнкции
и дизъюнкции
1 v 1 = 1

0

л 0 = 0
0 v 0 = 0

1 л 1

= 1

0 v 1 = 1 v 0=1

0 л 1 = 1 л 0 = 0

Аксиомы (3,4,5)Определяютоперации конъюнкции и дизъюнкции1 v 1 = 10 л 0 = 00 v 0 = 01

Слайд 15Принцип двойственности
Если в аксиомах 2 - 5, заданных

парами утверждений, произвести взаимную замену операций дизъюнкции и конъюнкции, а

также элементов 0 и 1, то из одного утверждения пары будет получено другое. Это свойство называется принципом двойственности.

Принцип двойственности Если в аксиомах 2 - 5, заданных парами утверждений, произвести взаимную замену операций дизъюнкции

Слайд 16Упражнение :
Какие выражения являются истинными, а какие -

ложными?
х2>0
x2

Слайд 17Упражнение :
Приведите отрицания к утверждениям:
На улице стоит ужасная жара.

Евклид был в Египте.
Если идет дождь, то светит солнце.

Упражнение :Приведите отрицания к утверждениям: На улице стоит ужасная жара. Евклид был в Египте. Если идет дождь,

Слайд 18Логическая функция

Из элементарных высказываний, применяя
операции булевой алгебры, можно получать
составные высказывания

любой сложности.
Истинность или ложность конкретного
составного высказывания зависит от истинности
или ложности входящих в него элементарных
высказываний. Так возникает понятие
логической функции, которую можно задать в
виде формулы или в виде таблицы.

Логическая функция Из элементарных высказываний, применяя операции булевой алгебры,

Слайд 19Формула алгебры высказываний определяется следующим образом:
1. Элементарное высказывание является формулой

алгебры высказываний.
2. Если Ф1 и Ф2 – формулы алгебры

высказываний, то (Ф1 & Ф2), (Ф1 ∨ Ф2) и ⎤Ф1 являются формулами алгебры высказываний.
3. Других формул алгебры высказываний нет.

Формула алгебры высказываний определяется следующим образом: 1. Элементарное высказывание является формулой алгебры высказываний. 2. Если Ф1 и

Слайд 20Примеры формул
алгебры высказываний от

трёх
логических переменных X1, X2 и X3:

(⎤X1 ∨ X2) & X3 ∨ ⎤X2 ,

⎤(⎤(X2 ∨ X3) ∨ ⎤X1).

Примеры формул алгебры высказываний от трёх логических переменных X1,

Слайд 21Таблица истинности
Табличное задание функции алгебры
логики называется её таблицей

истинности.
В таблице истинности наборы значений
логических переменных обычно

располагают
в порядке возрастания соответствующих
этим наборам двоичных чисел.

Таблица истинности Табличное задание функции алгебрылогики называется её таблицей истинности. В таблице истинности наборы значений

Слайд 22 Пример таблицы истинности функции F от трёх логических переменных X1,

X2, X3.

Слайд 23 Отметим, что таблица истинности от

n
переменных состоит из 2n +1 строк и n+1
столбцов. Число двоичных

наборов длины
n равно 2n. Таким образом, формирование
таблицы истинности конкретной булевой
функции от n переменных сводится к
заполнению нулями и единицами 2n
компонент её последнего столбца.

Отметим, что таблица истинности от nпеременных состоит из 2n +1 строк и

Слайд 24 Для любого выражения можно
проверить его значение, используя
таблицу

истинности, зная при
этом как ведут себя простейшие
логические функции.

Для любого выражения можнопроверить его значение, используятаблицу истинности, зная приэтом как ведут себя простейшиелогические

Слайд 25Пример таблицы истинности:

Слайд 26Пример 2:

Слайд 27 Для этого необходимо формулу
последовательно разложить на

более
простые подформулы и последовательно
(в обратном порядке)

построить таблицы
истинности этих подформул.

Построить таблицу истинности , заданную формулой алгебры высказываний.

Для этого необходимо формулу последовательно разложить на более простые подформулы и последовательно

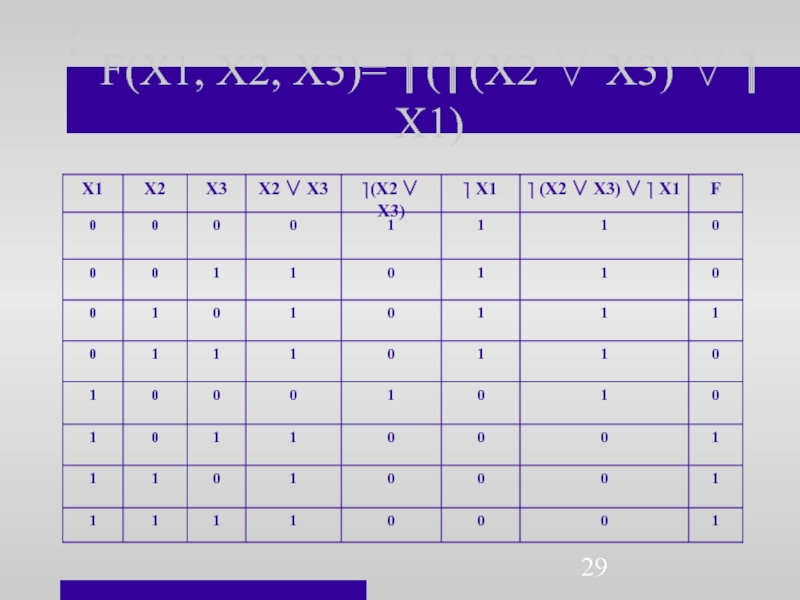
Слайд 28Например:
При построении таблицы истинности булевой
функции, заданной формулой

F(X1, X2, X3)= ⎤ (⎤ (X2 ∨ X3) ∨ ⎤

X1) ,
рассматривают подформулы:
1) X2 ∨ X3
2) ⎤ (X2 ∨ X3) ,
3) ⎤ X1
4) ⎤ (X2 ∨ X3) ∨ ⎤ X1.

Например: При построении таблицы истинности булевойфункции, заданной формулой F(X1, X2, X3)= ⎤ (⎤ (X2 ∨

Слайд 29F(X1, X2, X3)= ⎤ (⎤ (X2 ∨ X3) ∨ ⎤

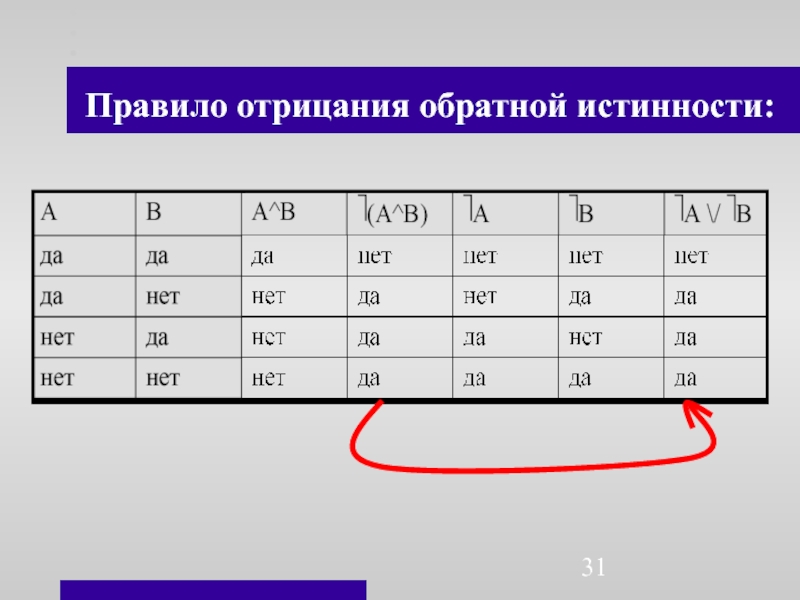
Слайд 30Правило отрицания обратной истинности:
⎤ (A ^ B) = (⎤A)

\/ (⎤B)
[не (а и б) = не а или не

б]
Стрелка Пирса. Основной базовый элемент логики, на котором построен все физические операции компьютера.
Отрицание истинности А и В тождественно тому, что ложно А или ложно В.

$Правило отрицания обратной истинности: ⎤ (A ^ B) = (⎤A) \/ (⎤B)[не (а и б) = не$

Слайд 31Правило отрицания обратной истинности:

Слайд 32Правило отрицания вариантов:

Слайд 33Упражнение:
Построить таблицы истинности:
А^⎤A
⎤ (A→B)
A^(A→B)
А\/⎤A
A→⎤B
⎤A→⎤B

$Упражнение:Построить таблицы истинности:А^⎤A⎤ (A→B)A^(A→B)А\/⎤AA→⎤B⎤A→⎤B$

Слайд 34Упражнение:
Построить отрицание

высказываний:
(⎤A)
(A^B^C)
⎤( ⎤( ⎤A))
(A\/B\/C)

$Упражнение: Построить отрицание высказываний:(⎤A)(A^B^C)⎤( ⎤( ⎤A))(A\/B\/C)$

Слайд 35Обратная задача:
по таблице истинности булевой
функции следует написать формулу
алгебры

высказываний.
Для этого введем определение
некоторых формул специального
вида.

Обратная задача:по таблице истинности булевой функции следует написать формулу алгебры высказываний. Для этого введем определениенекоторых

Слайд 36Элементарная конъюнкция
Элементарной конъюнкцией называется
логическое произведение переменных или

их отрицаний, в котором переменная
может входить не более одного раза.

Число
переменных или их отрицаний называют
её длиной. Длина элементарной
конъюнкции может быть равна единице.

Элементарная конъюнкция Элементарной конъюнкцией называется логическое произведение переменных или их отрицаний, в котором переменнаяможет входить не

Слайд 37Дизъюнктивная нормальная форма
Дизъюнктивной нормальной
формой (ДНФ) называется дизъюнкция
элементарных

конъюнкций. Число
элементарных конъюнкций в НДФ может
быть равно единице.

Дизъюнктивная нормальная форма Дизъюнктивной нормальнойформой (ДНФ) называется дизъюнкцияэлементарных конъюнкций. Числоэлементарных конъюнкций в НДФ можетбыть равно

Слайд 38Совершенная дизъюнктивная нормальная форма
Совершенной дизъюнктивной
нормальной формой (СДНФ)

называется
ДНФ, в которой все элементарные
конъюнкции имеют длину, равную числу
переменных.

Совершенная дизъюнктивная нормальная форма Совершенной дизъюнктивнойнормальной формой (СДНФ) называется ДНФ, в которой все элементарныеконъюнкции имеют

Слайд 39Примеры:
1. Формула ⎤X1 & X2 & X3 ∨

⎤X2 ∨ X2 & ⎤X3
является ДНФ.
2. Формула

(X1 & X3 ∨ ⎤X1 ) & X2
не является СДНФ.
3. Формулы X1 & ⎤X2 и ⎤X1 & X2 ∨ X1 & ⎤X2
являются СДНФ булевых функций от
переменных X1 и X2.

Примеры: 1. Формула ⎤X1 & X2 & X3 ∨ ⎤X2 ∨ X2 & ⎤X3 является ДНФ.

Слайд 40Свойство элементарной конъюнкции:
Длина элементарной конъюнкции

обращается в 1 ровно на одном наборе
значений переменных. Таким

образом,
каждому набору значений переменных
соответствует ровно одна такая
элементарная конъюнкция.

Свойство элементарной конъюнкции: Длина элементарной конъюнкции обращается в 1 ровно на одном наборе

Слайд 41Например,
набору (0,1,0) соответствует конъюнкция
⎤X1 & X2 & ⎤X3

.

На этом

свойстве основан алгоритм
нахождения формулы алгебры высказываний
булевой функции, заданной таблицей истинности.
Для каждого набора, на котором функция F=1,
находим элементарную конъюнкцию, которая
обращается в 1 на этом наборе. Дизъюнкция этих
конъюнкций является формулой алгебры
высказываний булевой функции F.

Например,набору (0,1,0) соответствует конъюнкция ⎤X1 & X2 & ⎤X3 .

Слайд 42 Если подформулу F1 формулы алгебры
высказываний F заменить

равносильной F1
формулой, то полученная формула F2
будет равносильна формуле F. Формула

F2
получена из F равносильным преобразованием.
Такой подход используется для нахождения
формулы равносильной исходной формуле. Для
реализации этого подхода разработан набор пар
равносильных формул.

Если подформулу F1 формулы алгебрывысказываний F заменить равносильной F1формулой, то полученная формула F2будет равносильна

Слайд 43Примеры пар равносильных формул:
А∨В и В∨А ; А∨А и А

; А∨1 и 1 ; А∨0 и А
- свойства

дизъюнкции;
А&В и В&А ; А&А и А ; А&1 и А ; А&0 и 0
- свойства конъюнкции;
А и А - закон отрицания отрицания;
А∨А&В и А - закон поглощения;
⎤(А∨В) и ⎤А&⎤В ; ⎤(А&В) и ⎤А∨⎤В
- законы де Моргана.

Примеры пар равносильных формул:А∨В и В∨А ; А∨А и А ; А∨1 и 1 ; А∨0 и

Слайд 44Проверка равносильности:
Наиболее просто проверку
осуществить следующим образом.
Для

этих формул построить таблицы
истинности Т1 и Т2. Формулы Ф1 и
Ф2

равносильны тогда и только
тогда, когда таблицы истинности Т1 и
Т2 одинаковы.

Проверка равносильности: Наиболее просто проверкуосуществить следующим образом.Для этих формул построить таблицыистинности Т1 и Т2.

Слайд 45Основы алгоритмизации

Слайд 46Определение алгоритма
Алгоритм решения задачи – система точно сформулированных правил, определяющих

процесс преобразования исходных данных в результат.

Определение алгоритмаАлгоритм решения задачи – система точно сформулированных правил, определяющих процесс преобразования исходных данных в результат.

Слайд 47Свойства алгоритма:
Определенность(точность)

Результативность

Массовость

Слайд 48Способы описания
Словесный
Формульно-словесный
Схемный
Язык операторных схем
Языки программирования

Слайд 49Схема определения алгоритма
Всякий алгоритм применяется к исходным (входным) данным и

выдает результаты (исходные данные).
Данные для своего размещения требуют памяти.
Элементарные шаги

алгоритма состоят из базовых действий, число которых конечно.
Последовательность шагов алгоритма должна быть однозначной.
Точность записи алгоритма связана с использованием жесткого синтаксиса.
Всякая алгоритмическая модель предполагает некоторый механизм исполнения алгоритмов.

Схема определения алгоритмаВсякий алгоритм применяется к исходным (входным) данным и выдает результаты (исходные данные).Данные для своего размещения

Слайд 50Символы записи процесса

- Процесс

- Подпрограмма

- Разветвление

Слайд 51Символы записи процесса (2)

- Соединитель

- Терминатор (начало или
конец алгоритма)

- Ввод и вывод
данных

Слайд 52Структуры алгоритмов:
Линейная

Разветвленная

Циклическая

Слайд 53 Пример линейной структуры:
начало
а, b
S = a + b
S
конец

Слайд 54Пример разветвленной структуры:
начало
а, b
b=0
Решений нет
m=a/b
m

конец
да
нет

Слайд 55Пример циклической структуры:
начало
i=1 to n step 2
s = s x

i
n
s=1
s
конец

Слайд 56Пример алгоритма:
Является ли натуральное число, введенное с клавиатуры

совершенным (равным сумме всех своих делителей)?
Введем N – натуральное число
В

ячейку S занесем ноль.
Зададим цикл от 1 до N/2 шагом 1.
Для каждого последующего i, если N/i=N\i, то S= S + i
После выхода из цикла сравним суммарное значение S с исходным натуральным числом N:
если S=N, то N – совершенное число, иначе N –
несовершенное число.
Конец алгоритма

Пример алгоритма: Является ли натуральное число, введенное с клавиатуры совершенным (равным сумме всех своих делителей)?Введем N

Слайд 57Блок-схема алгоритма:
начало
n
s = 0
i=1 to n/2
n/i=n\i
s = s + 1
s=n
«n-несовер-
шенное»
«n-

совер-
шенное»
конец
да
да
нет
нет

$Блок-схема алгоритма:началоns = 0i=1 to n/2n/i=n\is = s + 1s=n«n-несовер-шенное»«n- совер-шенное»конецдаданетнет$

Слайд 58Успехов в познании!!!

Скачать презентацию

Разделы презентаций

ЛЕКЦИЯ-ЛОГИКА.ppt

Содержание

Слайды и текст этой презентации

Слайд 1Введение в алгебру логики. Основы алгоритмизации.

Слайд 2Элементы логики

Слайд 3ЛогикаЛогика - это наука, изучающая методы доказательств и опровержений –

методы установления истинности или ложности одних высказываний (утверждений) на основе

Слайд 4Логическая функция Логическая функция – это

алгебраическое выражение, содержащие элементы алгебры логики, связанные между собой операциями,

Слайд 5Основные подходы к:Установление истинности высказыванийэмпирическийлогическийС помощью некоторых проверяющих действийНа основе

истинности других высказываний,чисто формально, с помощьюрассуждений.

Слайд 6 Основные логические связки

Слайд 7Инверсия (НЕ)⎤А = 1-А«не А»Отрицание истинно, если ложно исходное утверждение.Отрицание

ложно, если исходное утверждение истинно.L

Слайд 8Конъюнкция (И)А И В = а * b«А и В»Красивые

и умные – однозначная истинность составляющих суждений.Выражение истинно, если истинны

Слайд 9Дизъюнкция (ИЛИ)А ∨ В = a + b – a*b«А

или В»Составное суждение со связкой ИЛИ считается истинным, если истинно

Слайд 10Импликация (ЕСЛИ … ТО)А →В = ⎤А И В =

⎤а * б «А влечет В»Высказывание ложно только в том

Слайд 11Эквивалентность (ЕСЛИ И ТОЛЬКО ЕСЛИ)А ~ В «А, если и

только если В» Высказывание истинно, если А = В.Высказывание ложно

Слайд 12Неравнозначность (ЛИБО…ЛИБО) А ⊕ В =⎤А ИЛИ В = (1-a) + b

– (1-a) * b«либо А либо В »Высказывание истинно, когда

Слайд 13Аксиомы (1,2) Утверждает, что в алгебре логики рассматриваются

только двоичные переменныеОпределяет операцию отрицанияx = 0, если x –

Слайд 14Аксиомы (3,4,5)Определяютоперации конъюнкции и дизъюнкции1 v 1 = 10

л 0 = 00 v 0 = 01 л 1

Слайд 15Принцип двойственности Если в аксиомах 2 - 5, заданных

парами утверждений, произвести взаимную замену операций дизъюнкции и конъюнкции, а

Слайд 16Упражнение : Какие выражения являются истинными, а какие -

ложными?х2>0x2

Слайд 17Упражнение :Приведите отрицания к утверждениям: На улице стоит ужасная жара.

Евклид был в Египте. Если идет дождь, то светит солнце.