Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекции № 2 7
Содержание
- 1. Лекции № 2 7
- 2. Расчет каменных и армокаменных конструкций по предельным
- 3. Расчет каменных конструкций на внецентренное сжатие производится
- 4. Центральное сжатиеПри центральном сжатии напряжения по сечению
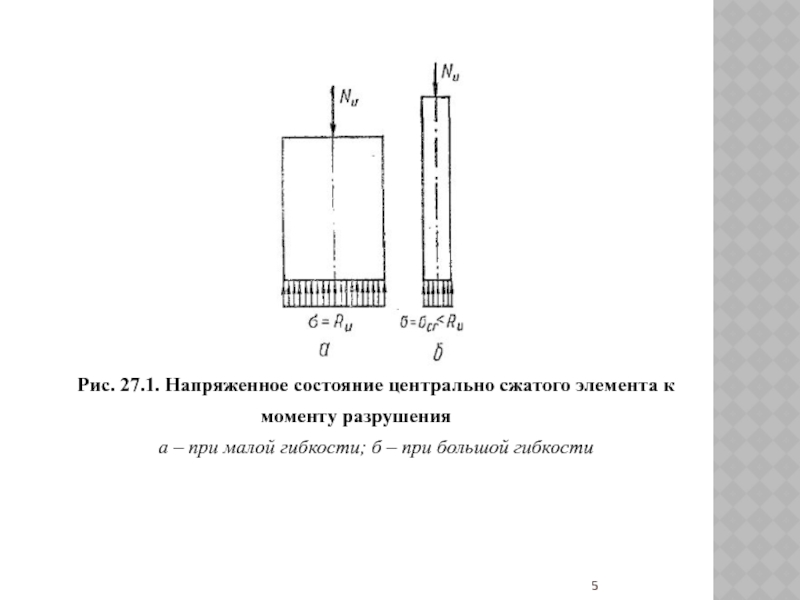
- 5. Рис. 27.1. Напряженное состояние центрально сжатого элемента
- 6. Слайд 6
- 7. Слайд 7
- 8. Коэффициент mg отражает влияние ползучести при длительном
- 9. Слайд 9
- 10. при упругой верхней опоре и жестком защемлении
- 11. Рис. 27.2. Определение расчетных длин сжатых элементов и коэффициентов mg и
- 12. Местное сжатие (смятие) кладкиПри опирании какой-либо конструкции
- 13. Слайд 13
- 14. Несущая способность элемента при местном сжатии с
- 15. Расчетная площадь сечения A определяется по следующим
- 16. при расчете на местную краевую нагрузку, приложенную
- 17. В этих случаях в расчетную площадь включается,
- 18. Рис. 27.3. Определение расчетных площадей сечения при местном сжатии:1-3 – номера участков, прилегающих к площади смятия
- 19. Внецентренное сжатиеВнецентренное сжатие является наиболее распространенным видом
- 20. Рис. 27.4. Виды эпюр напряжений при внецентренном
- 21. При расчете каменных элементов, работающих на внецентренное
- 22. Рис. 27.5. Расчетная схема при внецентренном сжатии кладкиа – прямоугольного сечения; б – таврового сечения
- 23. Расстояние от точки приложения силы до более
- 24. Уравнение для расчета неармированной кладки на внецентренное
- 25. При
- 26. При определении коэффициента продольного изгиба внецентренно сжатых
- 27. Расчет по раскрытию трещин производят по расчетным
- 28. Слайд 28
- 29. Скачать презентанцию
Расчет каменных и армокаменных конструкций по предельным состояниям первой группы (потеря несущей способности, потеря устойчивости формы, потеря устойчивости положения) производится, как правило, на воздействие расчетных нагрузок.Расчет каменных и армокаменных конструкций незаконченных
Слайды и текст этой презентации
Слайд 1Лекции № 27
РАСЧЕТ ЭЛЕМЕНТОВ КАМЕННЫХ КОНСТРУКЦИЙ
ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ПЕРВОЙ
ГРУППЫ
(ПО НЕСУЩЕЙ СПОСОБНОСТИ)
Слайд 2Расчет каменных и армокаменных конструкций по предельным состояниям первой группы
(потеря несущей способности, потеря устойчивости формы, потеря устойчивости положения) производится,
как правило, на воздействие расчетных нагрузок.Расчет каменных и армокаменных конструкций незаконченных зданий и сооружений производится на воздействие нормативной ветровой нагрузки, а для других нагрузок принимаются их расчетные значения.
Сцепление раствора с кирпичом и камнем отличается большой изменчивостью и зависит от многих случайных величин. Поэтому расчет неармированных каменных конструкций производится без учета сопротивления кладки растяжению и изгибу по неперевязанным сечениям (например, по горизонтальным швам), за исключением случаев расчета на сейсмические нагрузки.
Слайд 3Расчет каменных конструкций на внецентренное сжатие производится без учета сопротивления
растянутой зоны сечения. При больших эксцентриситетах производится дополнительная проверка сечения
по образованию и раскрытию трещин; в этом случае условно учитывается сопротивление кладки растяжению по неперевязанному сечению как косвенная характеристика возможного раскрытия трещин.Сопротивление кладки растяжению по неперевязанному сечению учитывается при расчете кладки на сейсмические воздействия. В этом случае при выполнении кладки должны соблюдаться специальные правила, повышающие надежность сцепления. Прочность сцепления проверяется при этом контрольными испытаниями в лабораторных и натурных условиях.
Слайд 4Центральное сжатие
При центральном сжатии напряжения по сечению элемента распределяются равномерно.
Разрушение таких элементов происходит в зависимости от их гибкости: либо
в результате исчерпания прочностных свойств кладки (σ = Ru) при коротких элементах (рис. 27.1, а), либо в результате потери устойчивости при критических напряжениях (σ = σcr), меньших, чем Ru при длинных элементах (рис. 27.1, б). На значение разрушающих усилий влияет длительность действия нагрузки.где N – расчетная продольная сила; R – расчетное сопротивление кладки сжатию; – коэффициент продольного изгиба; А – площадь сечения элемента; mg – коэффициент, учитывающий влияние прогиба сжатых элементов на их несущую способность при длительной нагрузке
Слайд 5Рис. 27.1. Напряженное состояние центрально сжатого элемента к моменту разрушения
а
– при малой гибкости; б – при большой гибкости
Слайд 8Коэффициент mg отражает влияние ползучести при длительном действии нагрузки, зависящее
от уровня загружения
где Ng – расчетная продольная сила от длительно
действующих нагрузок .При или - mg = 1
Расчетную высоту l0 каменных стен и столбов при определении и mg принимают в зависимости от условий опирания указанных элементов на горизонтальные и вертикальные опоры:
при шарнирном опирании на неподвижные в горизонтальном направлении опоры (жилые, общественные, промышленные здания) - l0= H (рис. 27.2, а);
Слайд 10при упругой верхней опоре и жестком защемлении в нижней опоре:
для однопролетных зданий - l0= 1,5H; для многопролетных зданий l0=
1,25H (рис. 27.2, б);для свободно стоящих конструкций при отсутствии связи их с перекрытиями или другими горизонтальными опорами l0= 2H (рис. 27.2, в);
для конструкций с частично защемленными опорными сечениями – с учетом фактической степени защемления, но не менее l0= 0,8H.
Если опоры жесткие, то расчетную высоту принимают: при сборных железобетонных перекрытиях l0=0,9H; при монолитных, опертых на стены по 4 сторонам, l0=0,8H, где H – в данном случае, расстояние между перекрытиями в свету.
Если нагрузкой является только собственный вес элемента в пределах рассчитываемого участка, то указанную расчетную высоту сжатых элементов следует умножать на коэффициент 0,75.
Слайд 12Местное сжатие (смятие) кладки
При опирании какой-либо конструкции не на все
сечение каменной кладки, а только на его часть, имеет место
деформация, которая называется местным сжатием, или смятием кладки.Сопротивление каменной кладки местному сжатию больше, чем осевому, т.к. прилегающие к нагруженному участки смежные незагруженные зоны препятствуют его деформации и тем самым увеличивают его несущую способность.
Опытами установлено, что расчетное сопротивление кладки при местном сжатии
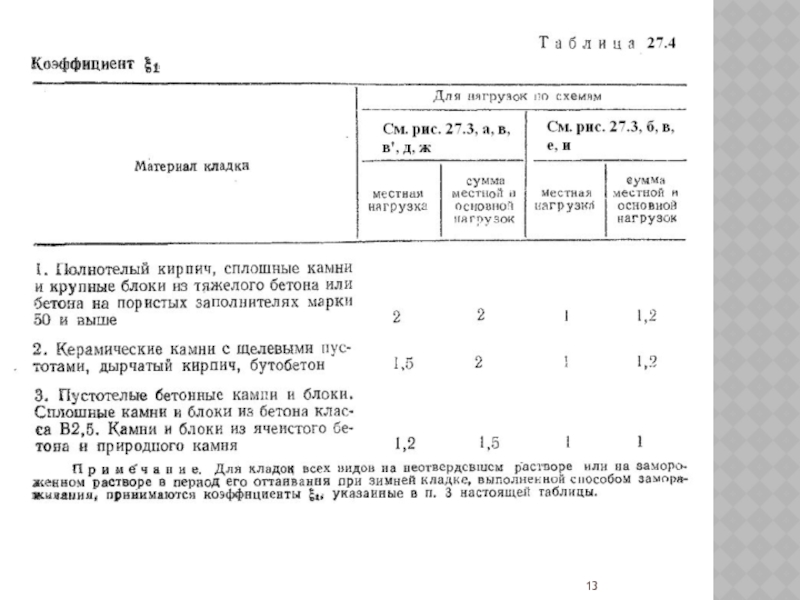
R – расчетное сопротивление кладки при осевом сжатии; Ac – площадь смятия, или местного сжатия, на которую передается нагрузка; A – расчетная площадь сечения при местном сжатии; ξ1 – граничный коэффициент, зависящий от материала кладки, места и характера приложения нагрузки.
Слайд 14Несущая способность элемента при местном сжатии с учетом указанного выше
увеличения сопротивления кладки проверяется как
где Nc – продольная сжимающая сила
от местной нагрузки; ψ – коэффициент полноты эпюры давления от местной нагрузки (при равномерном распределении давления ψ = 1; при треугольной эпюре: ψ = 0,5; d – коэффициент, учитывающий перераспределение напряжений в зоне местного сжатия (для кирпичной кладки d =0,5 – 1,5ψ.Если под опорами изгибаемых элементов не требуется установка распределительных плит, то допускается принимать ψd = 0,75 – для кладок из материалов поз. 1 и 2 табл. 27.4 и ψd = 0,5 – для кладок из материалов поз. 3 табл. 27.4
Слайд 15Расчетная площадь сечения A определяется по следующим правилам:
при местной нагрузке
по всей толщине стены в расчетную площадь включается участок длиной
не более толщины стены в каждую сторону от границы местной нагрузки (рис. 27.3, а);при расчете на местную краевую нагрузку, расположенную по всей толщине стены, расчетная площадь принимается равной площади смятия, а при расчете на сумму местной и основной нагрузок – сумме площадей смятия и участков стены длиной не более ее толщины в обе стороны (рис. 27.3, б);
При местной нагрузке в местах опирания концов прогонов и балок в расчетную площадь включается площадь участка стены шириной, равной глубине заделки опорного участка прогона или балки и длиной не более расстояния между осями двух соседних пролетов между балками (рис. 27.3, в); если расстояние между балками превышает двойную толщину стены, длина расчетной площади определяется как сумма ширины балки и удвоенной толщины стены (рис. 27.3, в’).
Слайд 16при расчете на местную краевую нагрузку, приложенную к угловому участку,
расчетная площадь принимается равной площади смятия, а при расчете на
сумму местной и основной нагрузки – площади (a+b)2 (рис. 27.3, г);при местной нагрузке, приложенной к части длины и толщины стены (рис. 27.3, д), расчетная площадь принимается равной (2C2+a) (2C1+b);
при расчете на местную краевую нагрузку, расположенную в пределах пилястры, расчетная площадь принимается равной площади смятия, а при расчете на сумму местной и основной нагрузок – равной площади b(a+b) (рис. 27.3, е);
При местной нагрузке, расположенной в пределах пилястры и части стены или простенка, увеличение расчетной площади по сравнению с площадью смятия следует учитывать только для нагрузки, равнодействующая которой приложена в пределах стены (полки) или же в пределах пилястры (ребра) с эксцентриситетом e0 >1/6L в сторону стены, где L - площадь смятия, e0 – эксцентриситет по отношению к оси площади смятия.
Слайд 17В этих случаях в расчетную площадь включается, кроме площади смятия,
часть площади сечения стены шириной с, равной глубине заделки опорной
плиты в кладку стены, и длиной в каждую сторону от края плиты не более толщины стены (рис. 27.3, ж);- если сечение имеет сложную форму, то при определении расчетной площади сечения не допускается учитывать участки, связь которых с загруженным участком недостаточна для перераспределения давления (участки 2 и 3 на рис. 27.3, з). В этом случае в расчетную площадь включают лишь площадь смятия и участки 1.
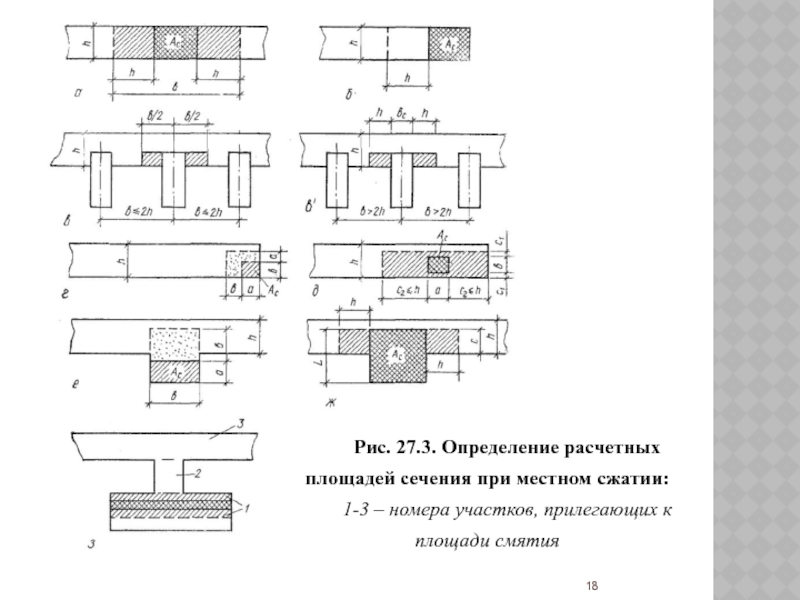
Слайд 18Рис. 27.3. Определение расчетных площадей сечения при местном сжатии:
1-3 –
номера участков, прилегающих к площади смятия
Слайд 19Внецентренное сжатие
Внецентренное сжатие является наиболее распространенным видом силового воздействия на
каменные конструкции.
Каменная кладка обладает упруго-пластическими свойствами, поэтому для расчета
неприменимы формулы для упругих материалов.Характер напряженного состояния кладки при внецентренном сжатии зависит от величины эксцентриситета e0 при приложении продольной силы N.
При небольших эксцентриситетах все сечение сжато (рис. 27.4, а). С ростом эксцентриситета эпюра напряжений становится двузначной (рис. 27.4, б), т.е. сечение испытывает сжатие и растяжение. При достаточно больших эксцентриситетах даже при малых нагрузках напряжения в растянутой зоне элемента могут превысить предельное сопротивление кладки растяжению при изгибе, и в растянутой зоне появятся горизонтальные трещины (рис. 27.4, в).
Слайд 20Рис. 27.4. Виды эпюр напряжений при внецентренном сжатии кладки
Появление трещин
не приводит к разрушению элемента, если напряжения в сжатой зоне
не превышают предельной величины, и нагрузка на него может быть увеличена, пока не используется прочность сжатой зоны сечения.Слайд 21При расчете каменных элементов, работающих на внецентренное сжатие, учитывается фактическая
несущая способность сжатой зоны кладки. При этом прочность сжатой зоны
вследствие сдерживающего влияния окружающей растянутой или растрескавшейся кладки (эффект обоймы), как и при местном сжатии, выше по сравнению с прочностью кладки на центральное сжатие. Этот эффект тем больше, чем меньше относительная высота сжатой зоны, т.е. чем больше значение эксцентриситета.Ширина и глубина раскрытия трещин ограничены.
Наибольшее значение эксцентриситета не должно превышать:
для основных сочетаний нагрузок – eu=0,9y;
для особых - eu=0,95y;
В стенах толщиной 25 см и меньше:
для основных сочетаний нагрузок – eu=0,8y;
для особых – eu = 0,85y.
y – расстояние от центра тяжести до края сечения в сторону эксцентриситета (рис. 25.5).
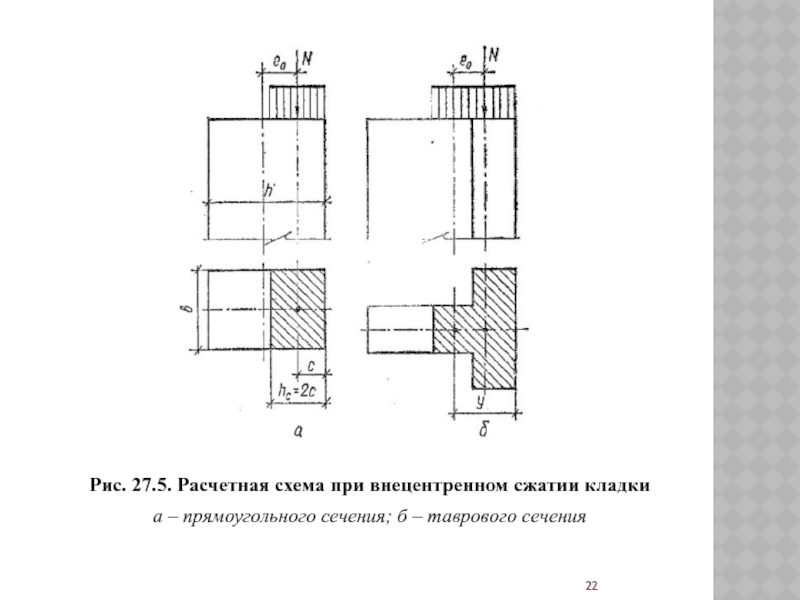
Слайд 22Рис. 27.5. Расчетная схема при внецентренном сжатии кладки
а – прямоугольного
сечения; б – таврового сечения
Слайд 23Расстояние от точки приложения силы до более сжатого края сечения
должно быть не менее 20 мм.
При расчете несущих и самонесущих
стен толщиной 25 см и менее следует учитывать случайный эксцентриситет еа, который должен суммироваться с эксцентриситетом продольной силы:еа = 2 см – для несущих стен;
еа = 1 см – для самонесущих стен, а также для отдельных слоев трехслойных несущих стен.
Для ненесущих стен случайный эксцентриситет не учитывается.
Если фактический эксцентриситет превышает предельное его значение, то растянутая зона кладки должна быть заармирована продольной арматурой.
Слайд 24Уравнение для расчета неармированной кладки на внецентренное сжатие при прямоугольной
эпюре напряжения вследствие проявления пластических деформаций:
где N – расчетная продольная
сила; R – расчетное сопротивление кладки сжатию; 1 – коэффициент продольного изгиба; Ас – площадь сжатой части сечения элемента; ω – коэффициент, учитывающий эффект обоймы; mg1 – коэффициент, учитывающий влияние прогиба сжатых элементов на их несущую способность при длительной нагрузке; eog – эксцентриситет от длительно действующей нагрузки.Слайд 26При определении коэффициента продольного изгиба внецентренно сжатых элементов и при
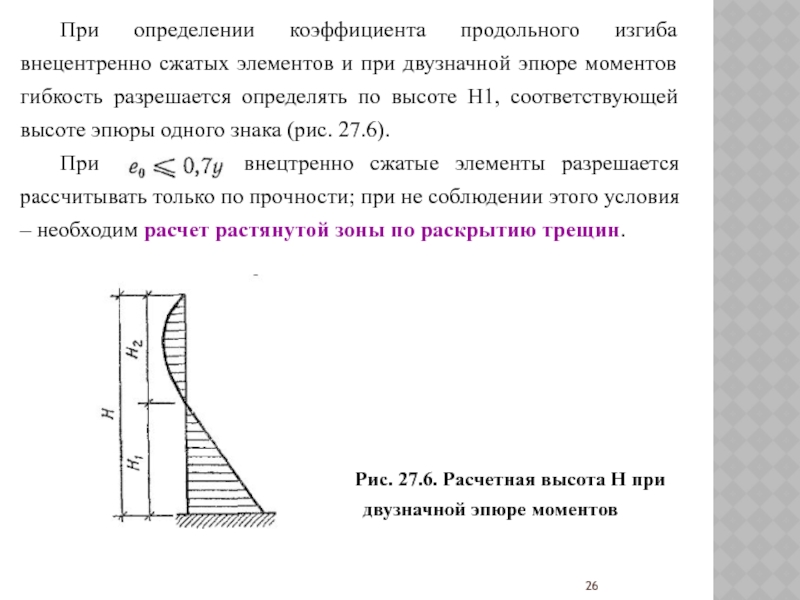
двузначной эпюре моментов гибкость разрешается определять по высоте H1, соответствующей
высоте эпюры одного знака (рис. 27.6).При внецтренно сжатые элементы разрешается рассчитывать только по прочности; при не соблюдении этого условия – необходим расчет растянутой зоны по раскрытию трещин.
Рис. 27.6. Расчетная высота Н при двузначной эпюре моментов
Слайд 27Расчет по раскрытию трещин производят по расчетным нагрузкам при основных
сочетаниях воздействий в предположении упругой работы кладки и сводится к
ограничению значения условного краевого напряжения растянутой зоныПосле преобразований и введения коэффициента условий работы кладки по раскрытию трещин γr:
Где I – момент инерции сечения в направлении изгибающего момента;Rbt – расчетное сопротивление кладки растяжению при изгибе по неперевязанному сечению.
Для элементов прямоугольного сечения формула имеет вид