Лекции №1,2

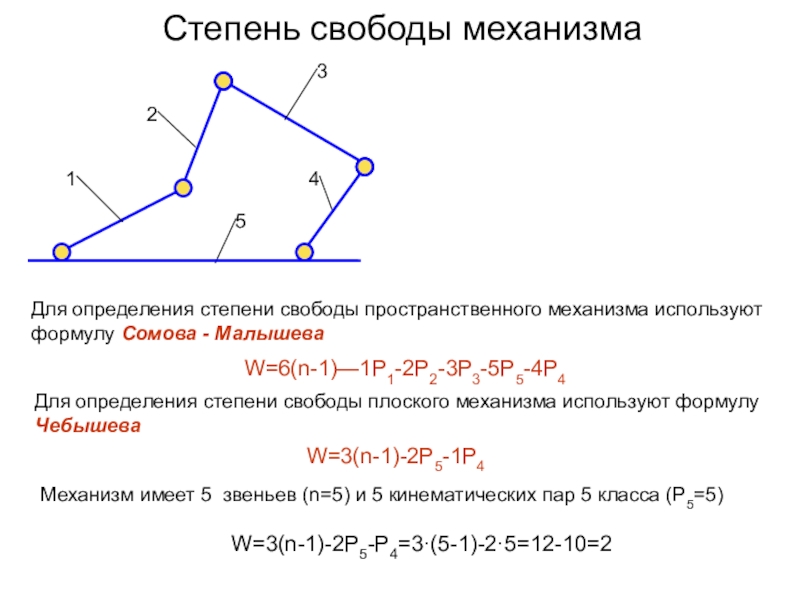
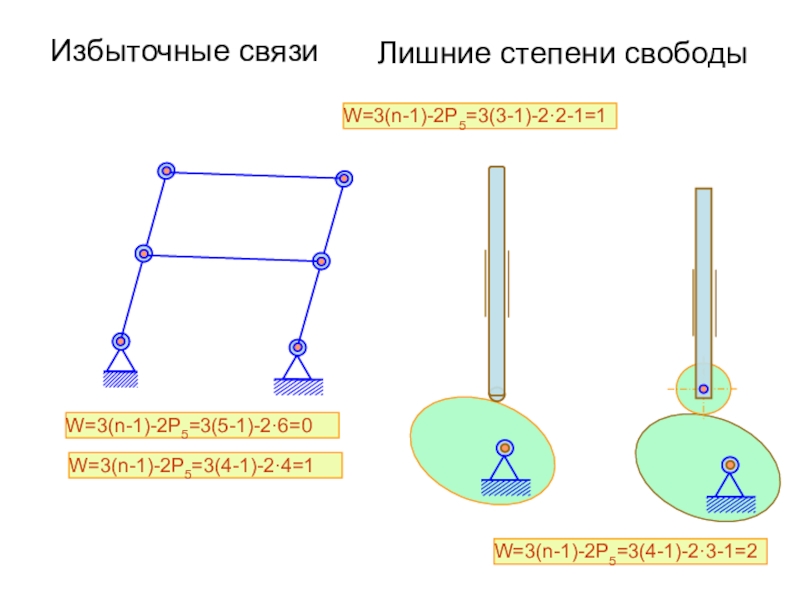
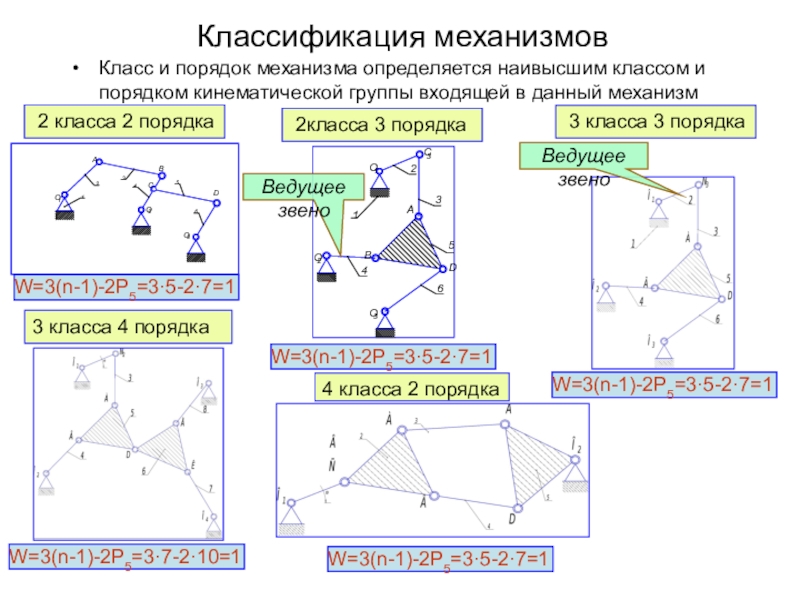
свободы механизма
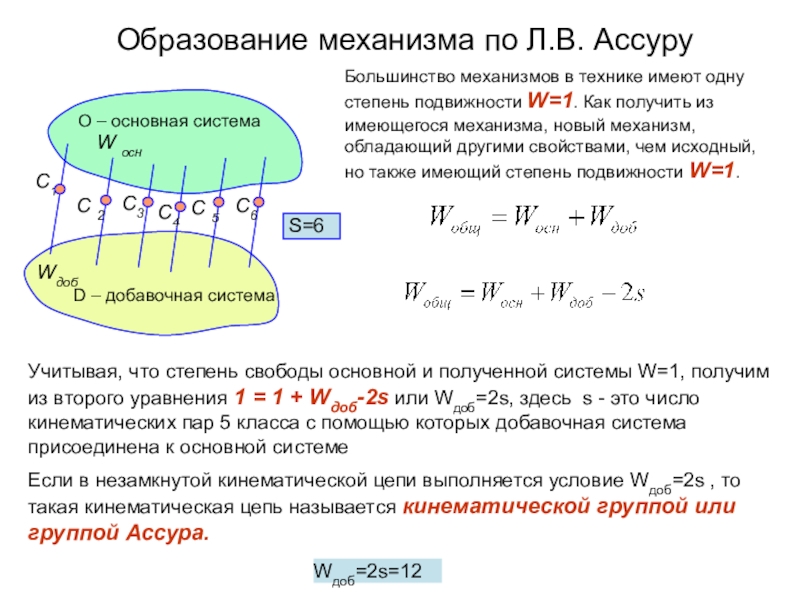
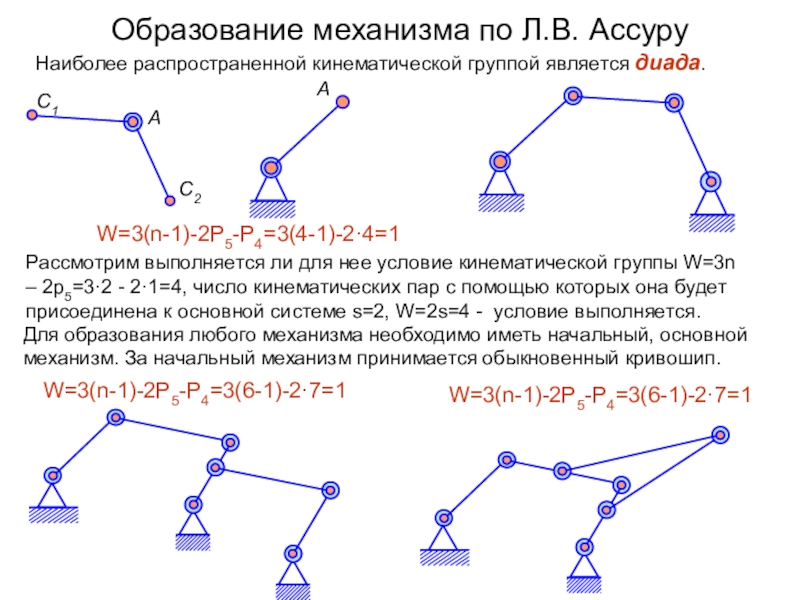
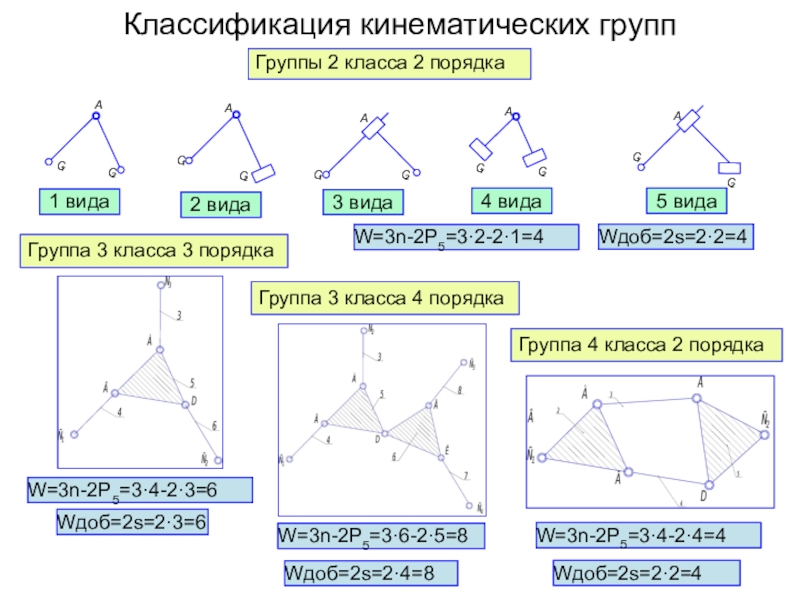
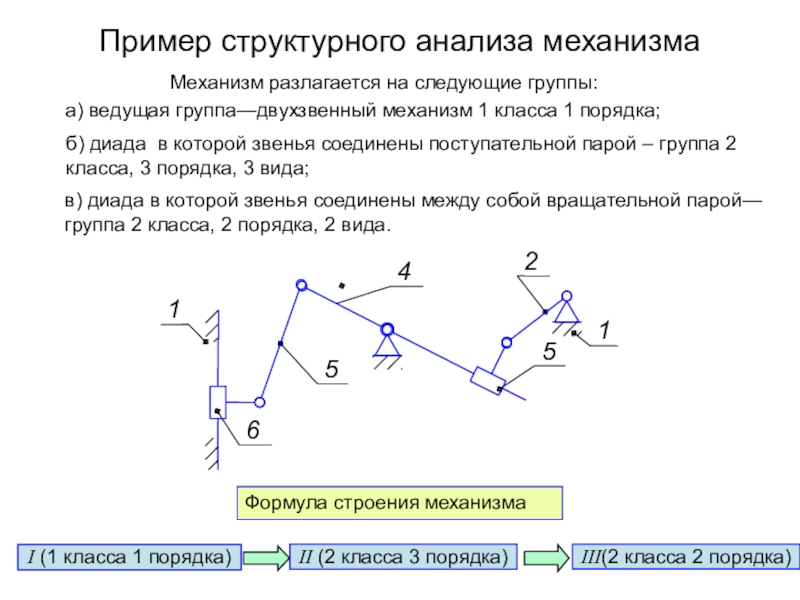
Образование механизма по Л. В. Ассуру
Основные понятия теории механизмов

Машины – это системы, служащие для передачи и преобразования механической работы.

Приборы – это системы, служащие для передачи и преобразования движений.

Механические приспособления – это системы, служащие для передачи и преобразования сил.

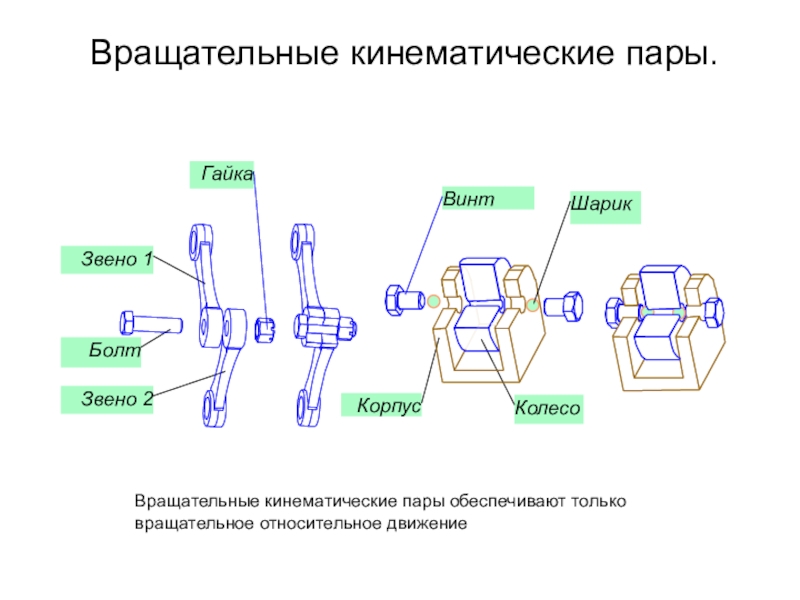
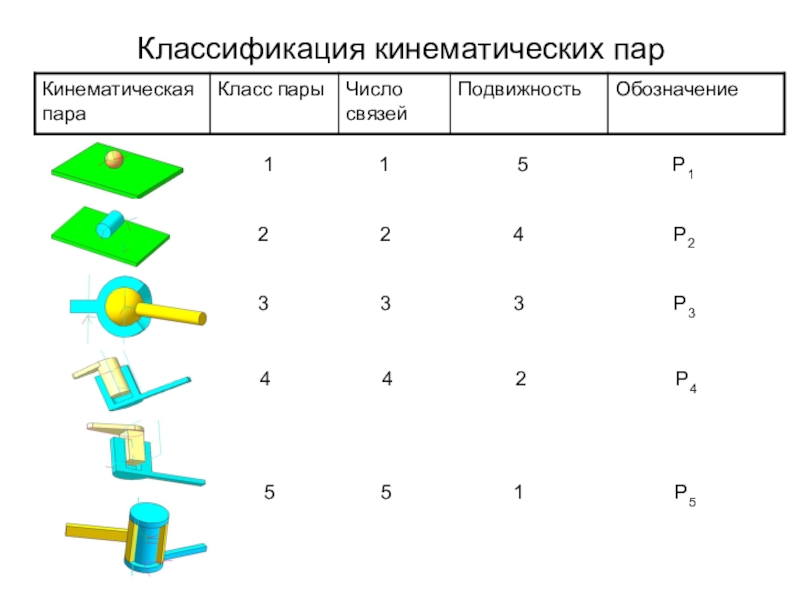
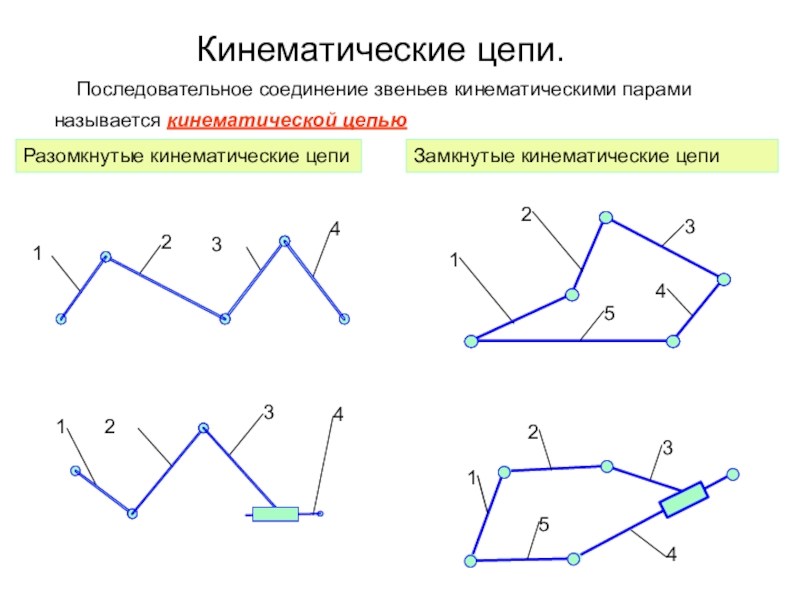
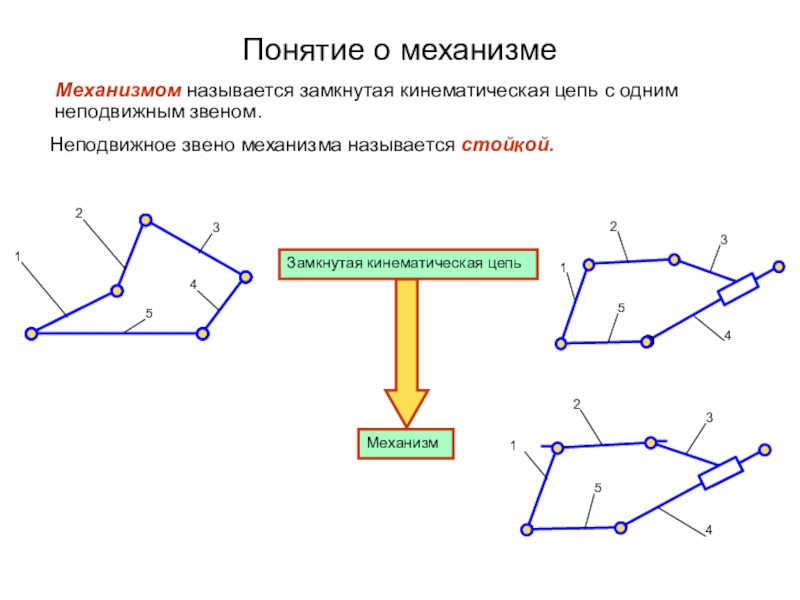
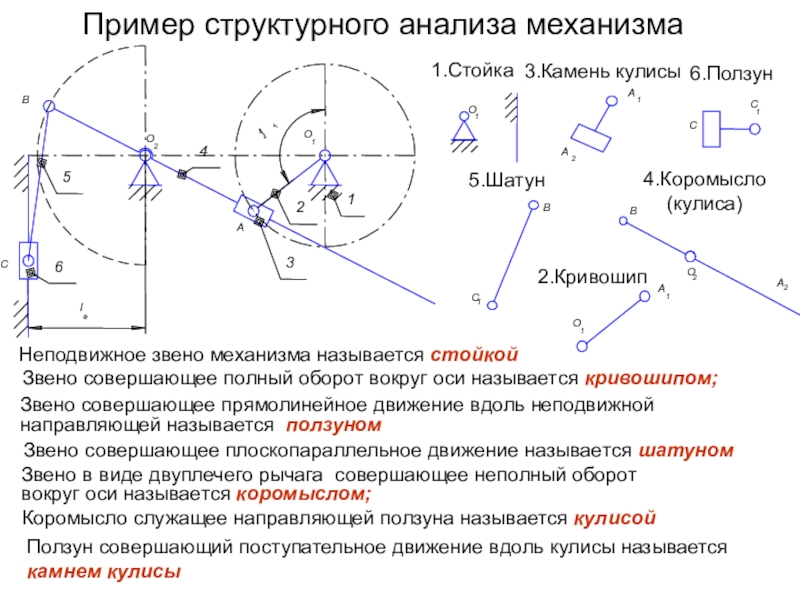
Кинематическая пара есть простейшее из сочленений, обеспечивающее между двумя соединяемыми звеньями тот или другой вид относительного движения.

Сочленения, допускающие пространственное относительное движение называются пространственными кинематическими парами.

Сочленение, допускающее плоское относительное движение называются плоскими кинематическими парами.

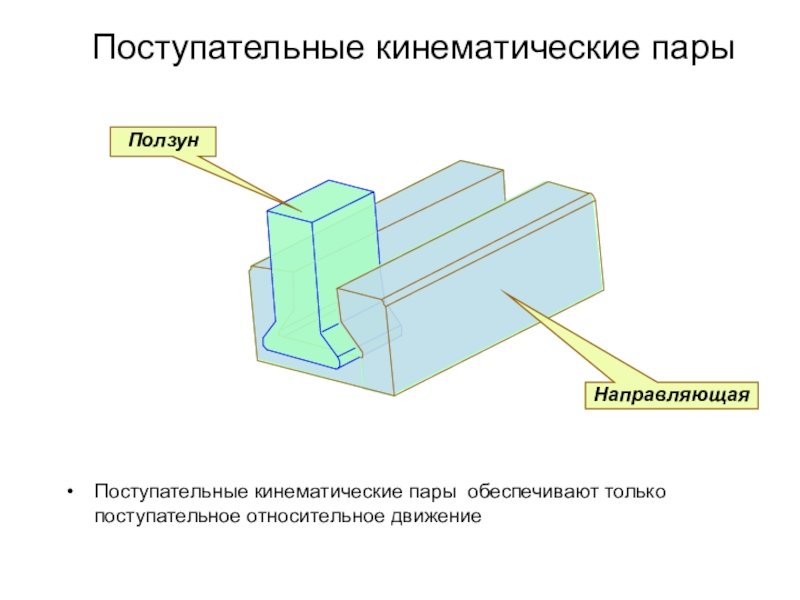
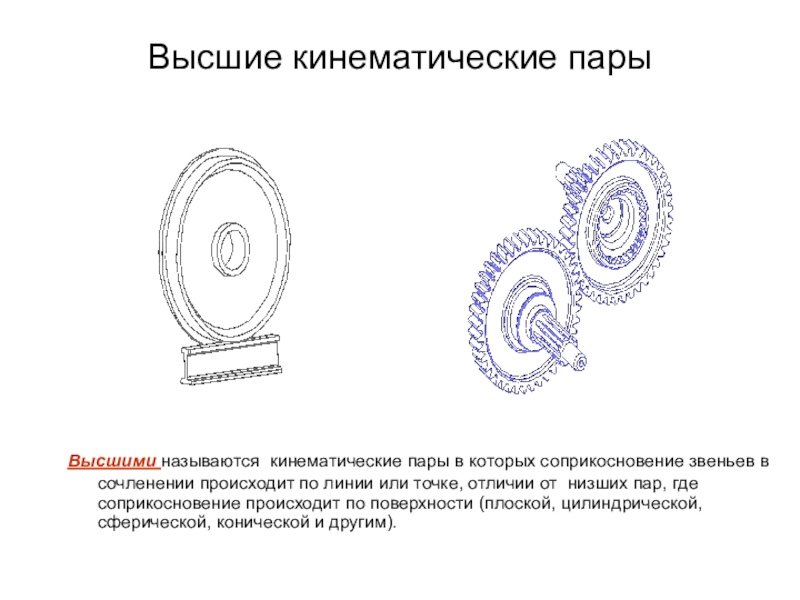
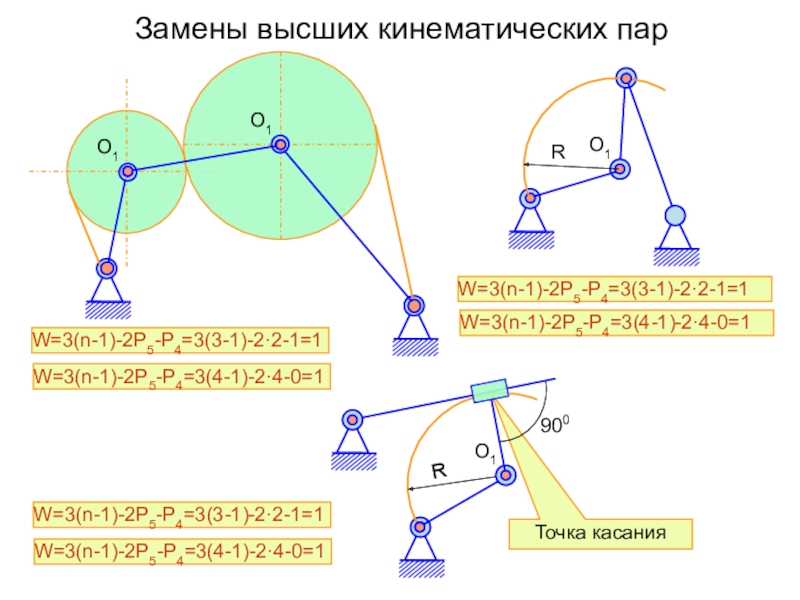
Плоские кинематические пары подразделяются на вращательные, поступательные и высшие

движение
Винт
Корпус
Колесо
Болт
Звено 1
Звено 2
Гайка
Шарик

Ползун

Направляющая

звеньев в сочленении происходит по линии или точке, отличии от

Разомкнутые кинематические цепи
Замкнутые кинематические цепи

звеном.
Замкнутая кинематическая цепь
Механизм
Неподвижное звено механизма называется стойкой.

всех звеньев механизма.
Для определения степени свободы механизма необходимо последовательным закреплением

Для превращения механизма в ферму было закреплено 2 звена (без учета стойки), и следовательно степень подвижности механизма равна 2

Для представленного механизма положение всех звеньев будут однозначно определены если будут задано положение двух любых звеньев (предположим звена 1 - 1 и звена 4 - 2)

Степень свободы механизма

Чебышева
W=3(n-1)-2P5-1P4
Механизм имеет 5 звеньев (n=5) и 5 кинематических пар 5

W=3(n-1)-2P5-P4=3·(5-1)-2·5=12-10=2

Для определения степени свободы пространственного механизма используют формулу Сомова - Малышева

W=6(n-1)—1Р1-2Р2-3Р3-5P5-4P4

степень подвижности W=1. Как получить из имеющегося механизма, новый механизм,

Учитывая, что степень свободы основной и полученной системы W=1, получим из второго уравнения 1 = 1 + Wдоб-2s или Wдоб=2s, здесь s - это число кинематических пар 5 класса с помощью которых добавочная система присоединена к основной системе

S=6

Если в незамкнутой кинематической цепи выполняется условие Wдоб=2s , то такая кинематическая цепь называется кинематической группой или группой Ассура.

Wдоб=2s=12

кинематической группы W=3n – 2p5=3·2 - 2·1=4, число кинематических пар

Для образования любого механизма необходимо иметь начальный, основной механизм. За начальный механизм принимается обыкновенный кривошип.

Наиболее распространенной кинематической группой является диада.

W=3(n-1)-2P5-P4=3(4-1)-2·4=1

W=3(n-1)-2P5-P4=3(6-1)-2·7=1

W=3(n-1)-2P5-P4=3(6-1)-2·7=1

порядка
Группа 4 класса 2 порядка
Группы 2 класса 2 порядка
1 вида
2

3 вида

4 вида

5 вида

W=3n-2P5=3·4-2·3=6

Wдоб=2s=2·3=6

W=3n-2P5=3·6-2·5=8

Wдоб=2s=2·4=8

Wдоб=2s=2·2=4

W=3n-2P5=3·4-2·4=4

W=3n-2P5=3·2-2·1=4

Wдоб=2s=2·2=4

кинематической группы входящей в данный механизм
4 класса 2 порядка
3

2класса 3 порядка

2 класса 2 порядка

W=3(n-1)-2P5=3·5-2·7=1

W=3(n-1)-2P5=3·5-2·7=1

W=3(n-1)-2P5=3·7-2·10=1

W=3(n-1)-2P5=3·5-2·7=1

W=3(n-1)-2P5=3·5-2·7=1

3 класса 3 порядка

Ведущее звено

Ведущее звено

совершающее полный оборот вокруг оси называется кривошипом;
Звено в виде двуплечего

Звено совершающее прямолинейное движение вдоль неподвижной направляющей называется ползуном

1.Стойка

2.Кривошип

3.Камень кулисы

4.Коромысло(кулиса)

5.Шатун

6.Ползун

Неподвижное звено механизма называется стойкой

Коромысло служащее направляющей ползуна называется кулисой

Ползун совершающий поступательное движение вдоль кулисы называется камнем кулисы

собой вращательной парой—группа 2 класса, 2 порядка, 2 вида.
а) ведущая

Механизм разлагается на следующие группы:

Формула строения механизма

б) диада в которой звенья соединены поступательной парой – группа 2 класса, 3 порядка, 3 вида;

I (1 класса 1 порядка)

II (2 класса 3 порядка)

III(2 класса 2 порядка)