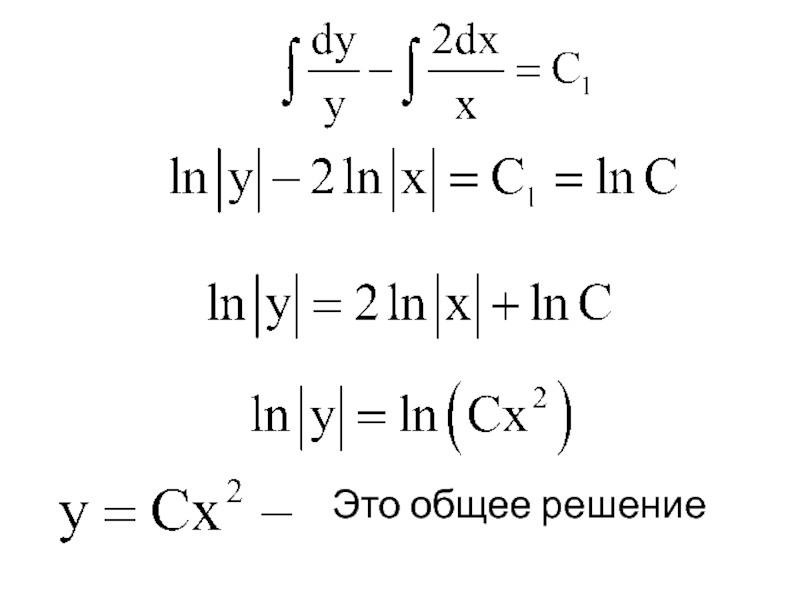Слайд 1Лекция 1. Основы математического анализа
Лектор: Войтик Виталий Викторович
Слайд 2Литература
Лобоцкая Н.Л. Основы высшей математики 2015, Москва
Ремизов А.Н. Максина
А.Г., Потапенко А.Я. Медицинская и биологическая физика 2013, Москва
Ремизов
А.Н., Максина А.Г. Сборник задач по медицинской и биологической физике 2014, Москва
Антонов В.Ф. Физика и биофизика (http://www.studmedlib.ru/boo k/ISBN9785970426777.html ) 2013, Москва
Слайд 3Определение производной
Если существует предел отношения
то функция f(x) называется дифференцируемой в
точке х, а значение предела называется производной от функции f(x)
в точке х и обозначается
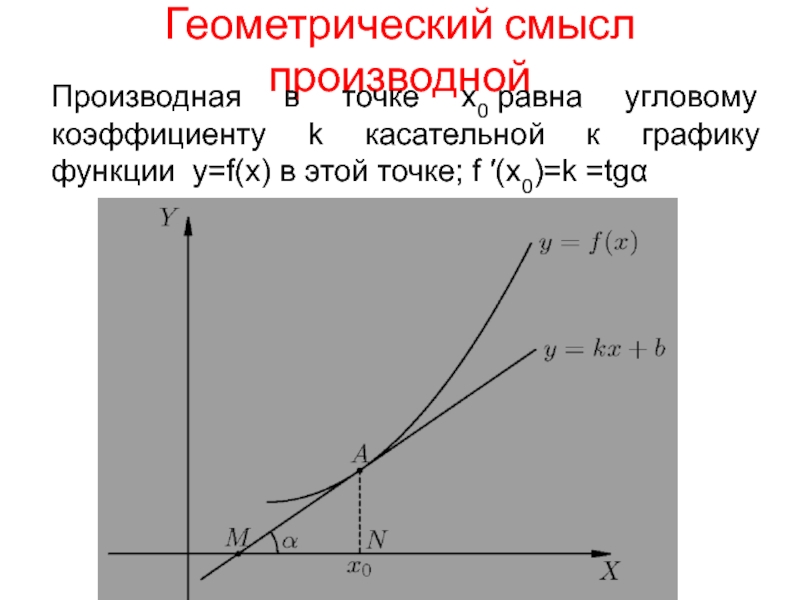
Слайд 4Геометрический смысл производной
Производная в точке x0 равна угловому коэффициенту k касательной
к графику функции y=f(x) в этой точке; f (x0)=k =tg
Слайд 6Производные элементарных функций
Слайд 7Пример. Найти производную функции
.
Сначала преобразуем данную функцию:
Производная сложной функции
Если
y=f(g(x)), то
где u=g(x)
Слайд 8Дифференциал функции
Дифференциалом df(x) функции f(x) в точке х называется произведение
производной от функции f(x) в этой точке на величину приращения
аргумента х
Слайд 9Связь между дифференциалом функции и её приращением
Дифференциал функции, в общем
случае отличаясь от приращения функции, представляет собой главную часть этого
приращения, линейную относительно приращения аргумента. В этом заключается аналитический смысл дифференциала. Отсюда следует, что при достаточно малых приращениях аргумента величина приращения функции приближённо равна дифференциалу этой функции
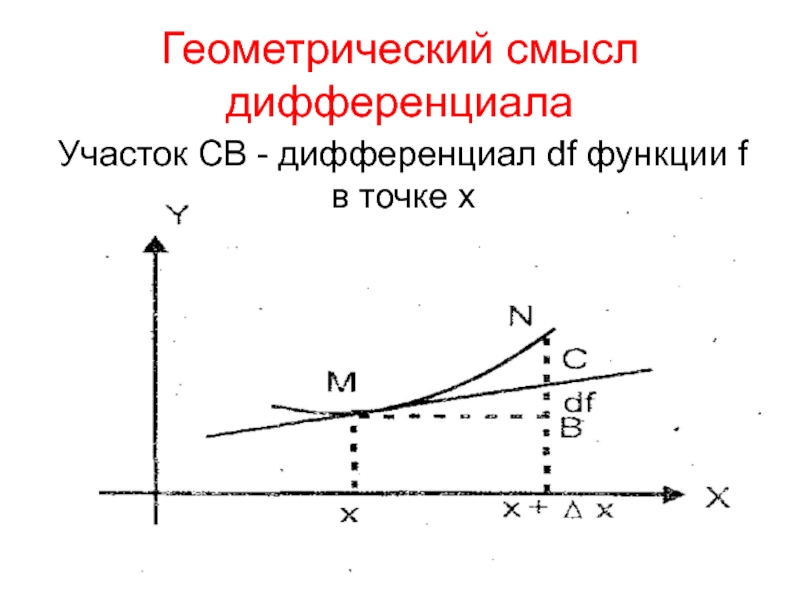
Слайд 10Геометрический смысл дифференциала
Участок СВ - дифференциал df функции f
в
точке х
Слайд 11Применение дифференциала для приближенных вычислений.
Оно основывается на приближённой формуле :
Δf=f’(x)Δx или
f(x+Δx)-f(x)=f’(x)Δx.
Отсюда мы можем вычислить значение функции в точке x+Δx:
f(x+Δx)=f(x)+f’(x)Δx,
если f(х) и f’(x) можно легко вычислить в точке x.
Слайд 13Применение производной при исследовании функции
Теорема о признаке возрастания и убывания
функции. Если производная функции положительна на некотором интервале, то функция
возрастает на этом интервале, наоборот если производная отрицательна, то функция убывает на этом интервале. Производная дифференцируемой функции в точке экстремума равна нулю.
Слайд 14Порядок действий при исследовании функции.
1. Найти область определения функции.
2.Найти производную
функции и определить точки, в которых производная не существует.
3.Приравнять производную
к нулю и
решить полученное уравнение
Слайд 15Корни этого уравнения являются экстремумами функции.
4. Найти критические точки
функции, как совокупность всех экстремумов и точек, в которых производная
не существует и отметить их на оси ОХ.
5.Определить знаки производных на интервалах, на которые критические точки делят область определения функции.
Слайд 16
6.По знаку производной найти интервалы возрастания и убывания функции.
7. Найти
точки экстремумов функции.
Слайд 17Первообразная функция.
Функция F(x) называется первообразной функцией функции f(x) на отрезке
[a, b], если в любой точке этого отрезка верно равенство:
F(x) = f(x).
Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
Слайд 18Неопределенный интеграл.
Определение: Неопределенным интегралом функции f(x) называется вся совокупность первообразных
функций F(x), которые определены соотношением:
Слайд 20Свойства интегралов:
где u, v, w – некоторые функции от х.
Слайд 21Методы интегрирования
А) Непосредственное интегрирование.
Слайд 22Б) Способ подстановки (замены переменных).
Сделаем замену
Пример. Найти неопределённый интеграл
Слайд 23В) Интегрирование по частям.
Способ основан на формуле:
Пример:
Слайд 24Определенный интеграл
Пусть на отрезке [ab] задана непрерывная функция y=f(x)
Слайд 25Найдем значения функции в этих точках и составим выражение, которое
называется интегральной суммой для функции f(x) на отрезке [a, b].
Sn
= f(1)x1 + f(2)x2 + … + f(n)xn =
Внутри каждого отрезка выберем некоторую точку .
x0 < 1 < x1, x1 < 2 < x2, … , xn-1 < n < xn.
Определение: Если при любых разбиениях отрезка [a, b] таких, что maxxi 0 и произвольном выборе точек i интегральная сумма
стремится к пределу S, который называется опреде-
ленным интегралом от f(x) на отрезке [a, b]:
Слайд 26Свойства определенного интеграла.
4) Если f(x) (x) на отрезке [a,
b] a < b, то
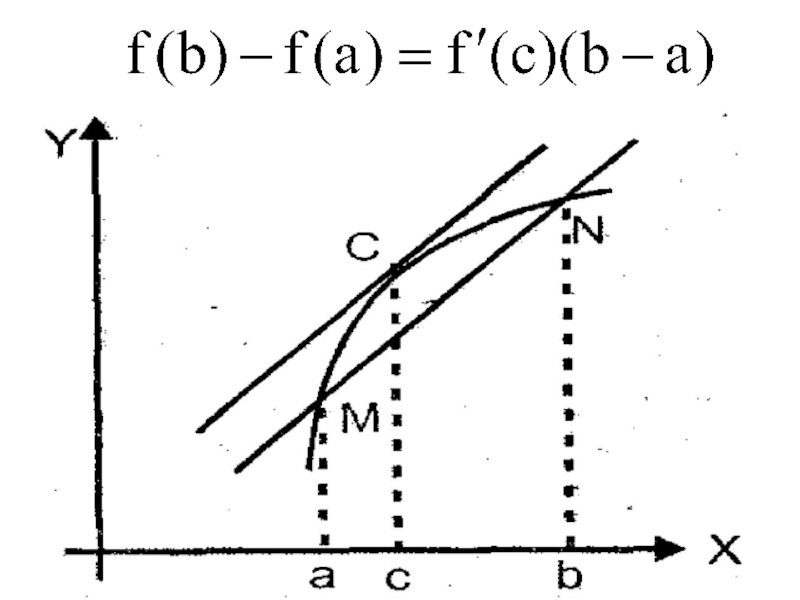
Слайд 275. Для произвольных чисел a, b, c справедливо равенство:
Теорема: (Теорема
Ньютона – Лейбница) Если функция F(x) – какая- либо первообразная
от непрерывной функции f(x), то
Слайд 31Дифференциальные уравнения первого порядка.
Уравнения с разделяющимися переменными
Дифференциальное уравнение первого
порядка имеет вид
F(x , y, y′) = 0 .
Если
это уравнение разрешено относительно y′ , то это уравнение имеет вид:
y′ = f (x , y) или dy=f (x , y)dx
Общим решением уравнения будет функция y=y(x ,C), зависящая от х и от одной произвольной постоянной, и обращающая это уравнение в тождество.
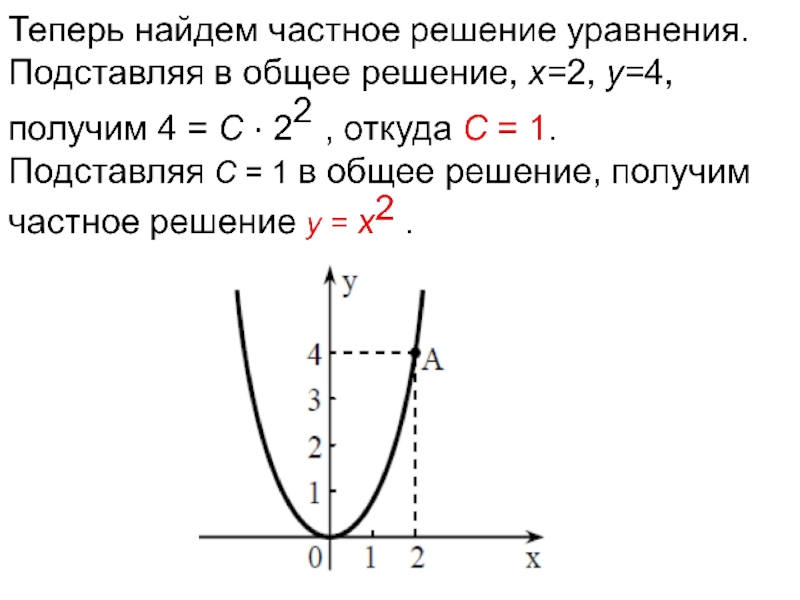
Слайд 32Частным решением уравнения будет решение y= y( x ,C0 ),
полученное из общего при фиксированном значении С, удовлетворяющее заданным начальным
условиям: y = y0 при x = x0. Другими словами: найти интегральную кривую уравнения, проходящую через заданную точку M0 (x0,y0 ).
Дифференциальное уравнение вида
P1 (x)Q1(y)dx+P2(x)Q 2 (y) dy =0,
где P1 (x ), P2 (x ) – функции только от х, а Q1(y), Q2(y) – функции только от у, называется уравнением с разделяющимися переменными.
Слайд 33Делением обеих частей уравнения на произведение Q1 (y)P2 (x )
может быть приведено к уравнению с разделенными переменными:
Общим интегралом уравнения
будет:
Слайд 34Пример. Дано уравнение
Найти частное решение этого уравнения, удовлетворяющее начальному условию
y = 4
при x = 2 .
Уравнение имеет
вид:
Разделяя переменные, получим:
Интегрируем:
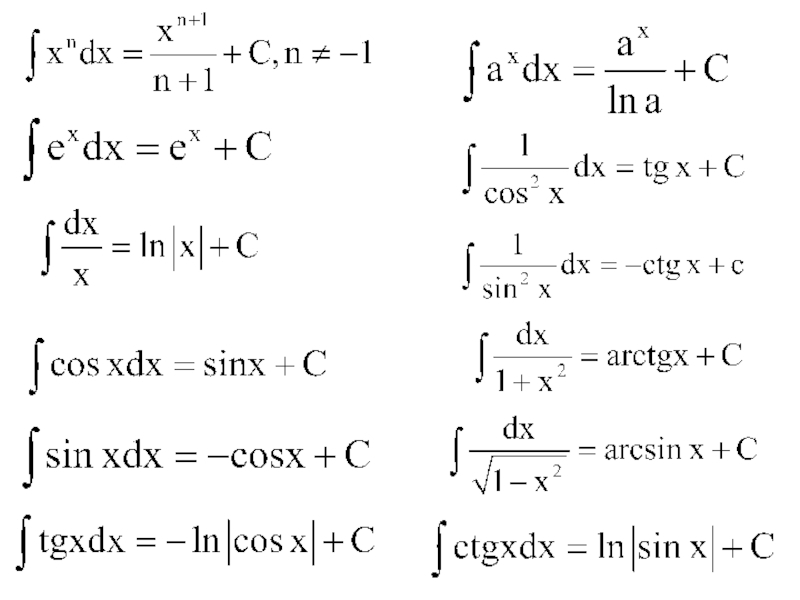
![Первообразная функция.Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в любой точке этого](/img/thumbs/b8b107a8b3c5be73851578f3159289d3-800x.jpg "Лекция 1. Основы математического анализа Первообразная функция.Функция F(x) называется первообразной функцией функции f(x) на отрезке [a,")
![Определенный интеграл Пусть на отрезке [ab] задана непрерывная функция y=f(x)](/img/thumbs/c07afd600393ffb0c98468c330455a09-800x.jpg "Лекция 1. Основы математического анализа Определенный интеграл Пусть на отрезке [ab] задана непрерывная функция y=f(x)")
![Свойства определенного интеграла.4) Если f(x) (x) на отрезке [a, b] a < b, то](/img/thumbs/c0c356b2d48dd0de91e25dbf270fbe48-800x.jpg "Лекция 1. Основы математического анализа Свойства определенного интеграла.4) Если f(x) (x) на отрезке [a, b] a < b, то")
