Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 12
Содержание
- 1. Лекция 12
- 2. Проблема устойчивости атмосферы планетБарометрическая формула Больцмана справедлива
- 3. В верхних слоях из-за разреженности атмосферы столкновения
- 4. В астрономии считают устойчивой атмосферу, средняя скорость
- 5. Энергия движения молекулИз закона распределения молекул по
- 6. Поступательное перемещение не единственно возможный вид
- 7. Степени свободыЧисло степеней свободы механической системы -
- 8. Положение любого абсолютно твердого тела задается тремя
- 9. Изменение координат центра масс происходит в результате
- 10. Количество степеней свободы, которыми обладает молекула газа,
- 11. Молекулы двухатомных газов (Н2, O2, N2) можно
- 12. Молекулы трехатомных газов, не вытянутые в линейную
- 13. Итак, общее количество степеней свободы определяется структурой
- 14. При подсчете числа i следует учесть, что
- 15. C колебательным движением сопряжено два вида энергии
- 16. Чтобы получить внутреннюю энергию Uμ одного моля
- 17. Положение материальной точки (одноатомной молекулы) задаётся тремя
- 18. Теплоемкость двухатомного газа.
- 19. Теплоемкость многоатомного газа. Многоатомную молекулу классическая статистическая
- 20. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Лекция 12
1. Проблема устойчивости атмосферы планет
2. Закон о равнораспределении энергии
по степеням свободы молекулы.
Слайд 2Проблема устойчивости атмосферы планет
Барометрическая формула Больцмана справедлива для Т =
const, g = const. В действительности эти условия не выполняются,
особенно в отношении температуры. Из-за интенсивного ультрафиолетового излучения Солнца, температура верхних слоев атмосферы Земли достигает 1800К. В результате кинетическая энергия молекул может превосходить гравитационную энергию связи, удерживающую молекулы у Земли.Слайд 3В верхних слоях из-за разреженности атмосферы столкновения молекул редки, и
молекула, имеющая скорость больше второй космической (11,2 км/с) беспрепятственно улетает
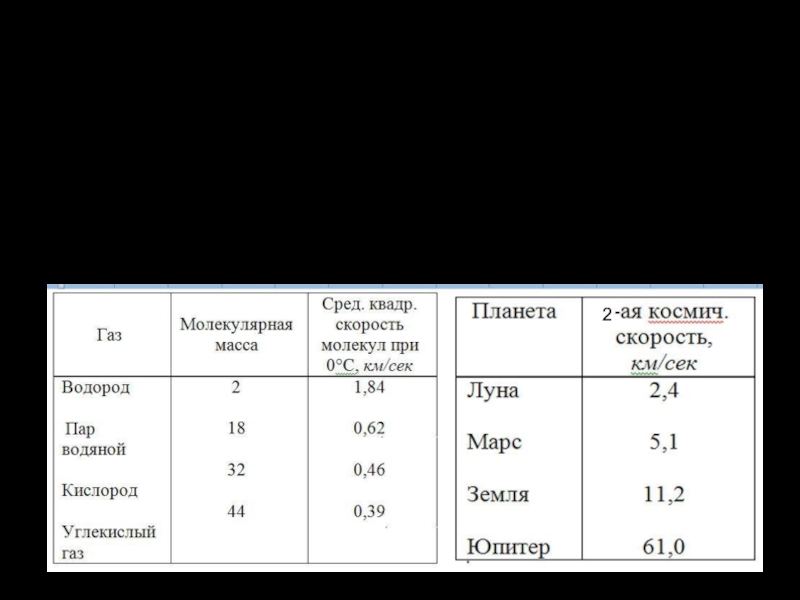
в космос.Скорость движения молекул пропорциональна , следовательно, легкие газы: водород, гелий, уходят из атмосферы в первую очередь. Для любой планеты устойчивость атмосферы зависит от силы тяготения, температуры верхних слоев её атмосферы и молекулярной массы частиц.Слайд 4В астрономии считают устойчивой атмосферу, средняя скорость молекул которой не
превышает 0,2 от второй космической скорости. Если средняя скорость составляет
0,25 от 2-ой космической, атмосфера рассеивается за 50 000 лет, а если 0,33 — всего за несколько недель. Ниже приведены сведения о среднеквадратичной скорости молекул газов и 2-ой космической скорости некоторых планет.2
2
Слайд 5Энергия движения молекул
Из закона распределения молекул по скоростям Максвелла следует,
что средняя энергия < ε > движения каждой молекулы равна
(3/2)kT. В рамках тех предположений, в которых установлен закон распределения Максвелла, молекулы рассматрива-ются как материальные точки. Для материаль- ной точки, лишенной внешних связей возможен только один вид движения - поступательный. Таким образом, величина (3/2)kT представляет собой среднюю энергию поступательного движения молекулы. Эта энергия определяется только температурой и не зависит от массы молекулы.Слайд 6Поступательное перемещение не единственно возможный вид движения молекул. Возможно
также вращение молекул вокруг произвольной оси, проходящей через ее центр
масс, и взаимные колебания атомов, входящих в состав молекулы. Оба эти вида движения также несут в себе определенную энергию.На них также распространяется тепловая энергияСлайд 7Степени свободы
Число степеней свободы механической системы - это количество независимых
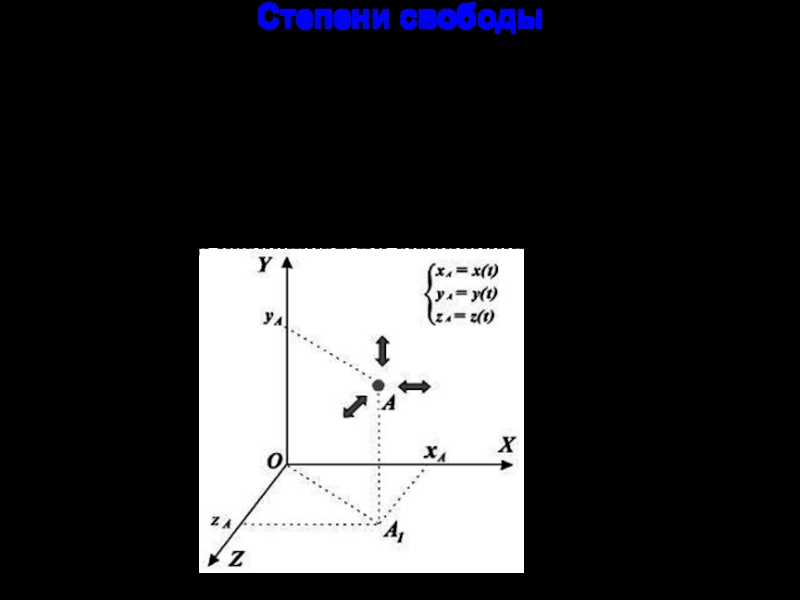
величин, с помощью которых может быть задано положение системы. Так,
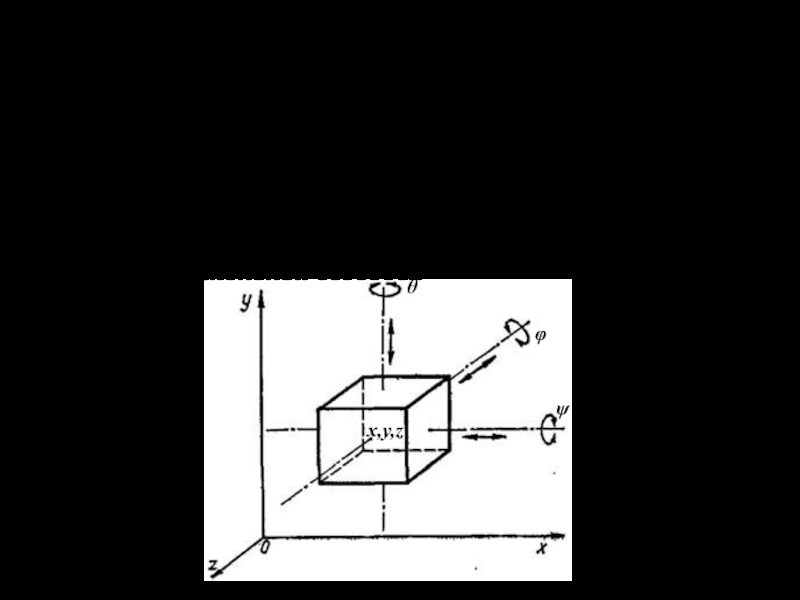
например, положение материальной точки в пространстве полностью задается тремя декартовыми координатами (x,y,z).Слайд 8Положение любого абсолютно твердого тела задается тремя декартовыми координатами (x,y,z)
центра масс и тремя углами (θ,φ,ψ) определяющими положение взаимно перпендикулярных
осей, связанных с телом, в выбранной системе координат. Таким образом, абсолютно твердое тело имеет 6 степеней свободы.x,y,z
θ
φ
ψ
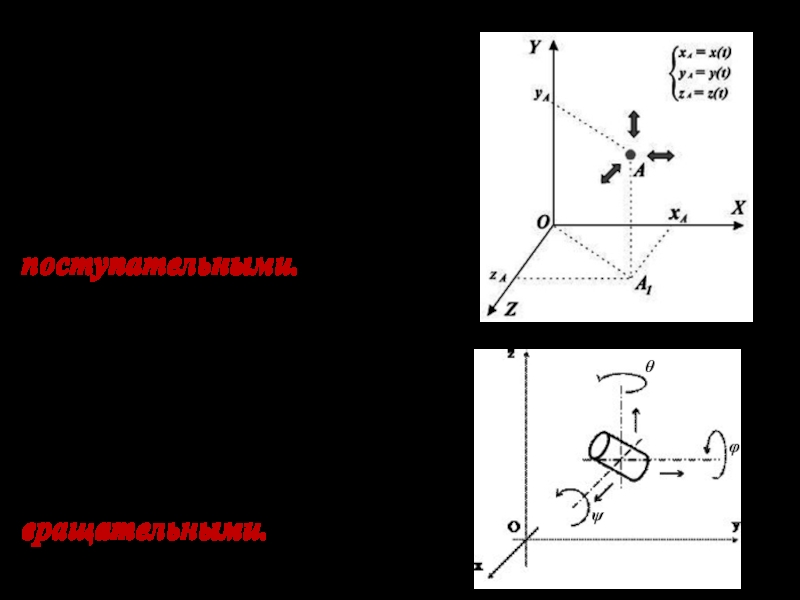
Слайд 9Изменение координат центра масс происходит в результате поступательного перемещения тела.
Соответствующие степени свободы называют поступательными.
Изменение углов (θ,φ,ψ) происходит в
результате вращения тела. Соответствующие степени свободы называют вращательными.θ
φ
ψ
Слайд 10Количество степеней свободы, которыми обладает молекула газа, зависит от ее
структуры. Молекула одноатомного газа (He, Ne, Ar, Kr, Xe) может
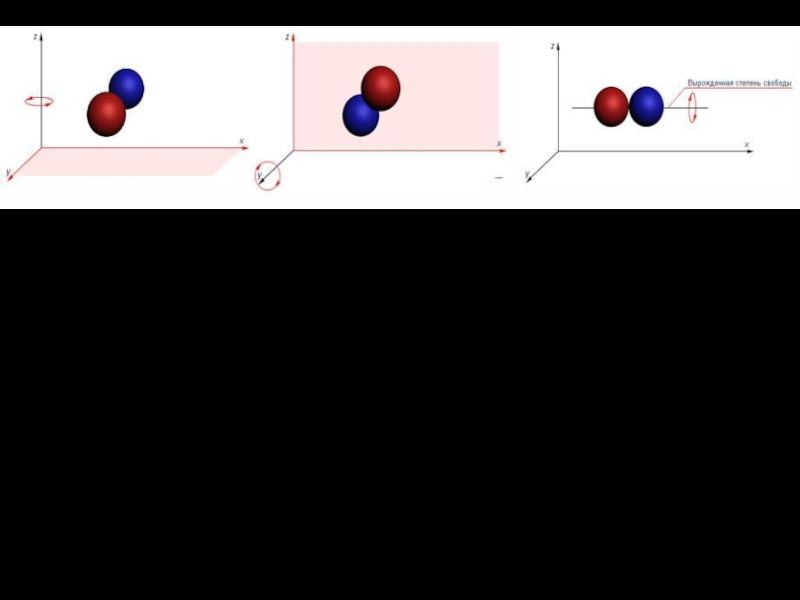
рассматриваться как материальная точка, поскольку практически вся масса атома сосредо- точена в ядре малых размеров. Такая молекула обладает тремя поступательными степенями свободы.Слайд 11Молекулы двухатомных газов (Н2, O2, N2) можно представить себе как
две материальные точки, связанные жесткой или упругой связью. Такая молекула
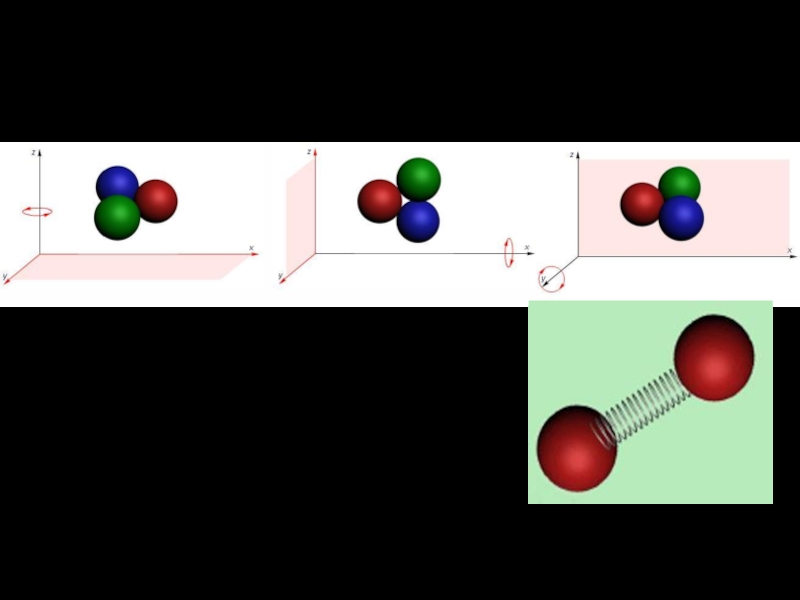
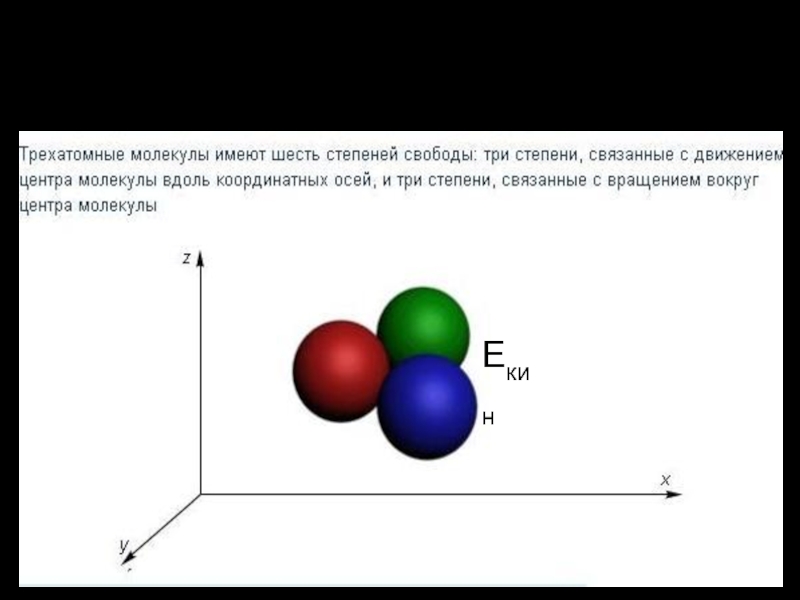
обладает тремя поступательными степенями свободы и двумя вращательными. На рис. показаны две возможные взаимно перпендикулярные оси вращения, соответствующие этим степеням свободы. Вращение вокруг третьей оси (линии связи двух атомов) не изменяет положения системы, поэтому третья вращательная степень свободы у данной молекулы отсутствует.Слайд 12Молекулы трехатомных газов, не вытянутые в линейную цепочку, обладают двумерной
или трехмерной структурой. Они могут вращаться вокруг трех взаимно перпендикуляр-
ных осей и, в итоге, имеют все шесть степеней свободы.Если связь между атомами в молекуле не жесткая, а упругая, то становится возможным еще один вид движения колебания атомов относительно положения их равновесия внутри самой молекулы.
С этим движением связывают колебательные степени свободы. Их столько, сколько упругих связей содержит молекула.
Слайд 13Итак, общее количество степеней свободы определяется структурой молекулы.
Закон равнораспределения энергии
по степеням свободы
В статистической физике сформулирован закон равнораспределения энергии, согласно
которому на каждую степень свободы молекулы приходится в среднем одинаковая кинетическая энергия теплового движения, равная (1/2)kT. Это означает, что среднее значение энергии одной молекулы при одной и той же температуре будет тем больше, чем больше у нее количество степеней свободы i, то естьСлайд 14При подсчете числа i следует учесть, что с поступательной и
вращательной степенями свободы связан только один вид энергии кинетическая
энергия.Екин
Слайд 15C колебательным движением сопряжено два вида энергии кинетическая и
потенциальная (потенциальной энергией обладают атомы молекулы при деформировании упругой связи
в ходе их колебаний).Таким образом, на колебатель- ную степень свободы молекулы приходится не одна, а две половинки kT. В результате, число степеней свободы i следует подсчитывать следующим образом:i = nпост + nвращ + 2nкол
где nпост, nвращ, nкол соответственно число поступательных, вращательных и колебательных степеней свободы молекулы.
Екин
Епот
Слайд 16Чтобы получить внутреннюю энергию Uμ одного моля идеального газа, нужно
среднюю энергию молекулы умножить на число молекул в одном
моле, то есть на число Авогадро NA.Uμ = NA = (i/2)NAkT = (i/2)RT
В результате получаем, что молярная теплоемкость при постоянном объеме
Молярная теплоемкость при постоянном давлении
Обозначим отношение
Величину γ называют показателем адиабаты
Слайд 17Положение материальной точки (одноатомной молекулы) задаётся тремя координатами (x, y,
z), поэтому она имеет три степени свободы:
Внутренняя энергия
Теплоемкости:
Показатель адиабаты
Теплоемкость одноатомного газа.
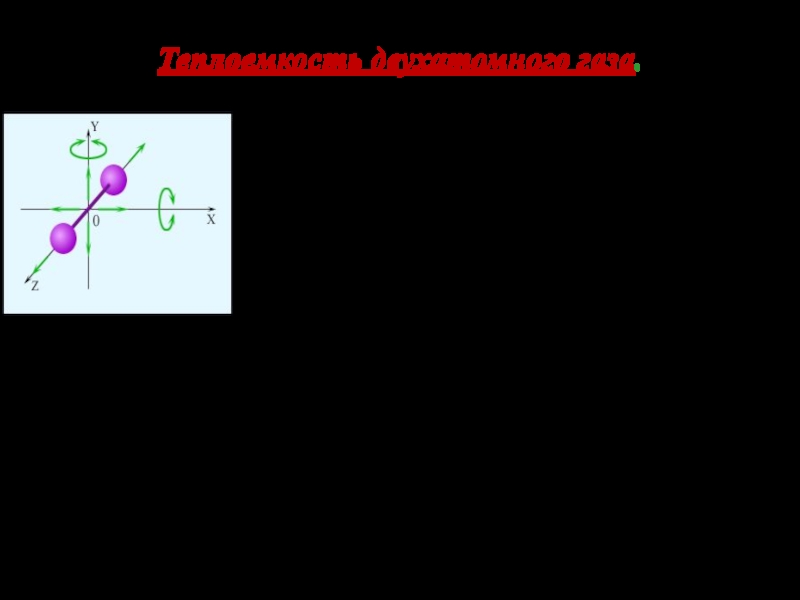
Слайд 18Теплоемкость двухатомного газа.
Двухатомная
молекула обладаеттремя поступательными степенями
свободы и двумя вращательными :
Слайд 19Теплоемкость многоатомного газа.
Многоатомную молекулу классическая статистическая физика рассматривает как
абсолютно твердое тело, которое может двигаться поступательно в трех взаимно
перпендикулярных направлениях и может вращаться вокруг трех взаимно перпендикулярных осейЧисло степеней свободы:
Внутренняя энергия:
Теплоемкость:
γ = 4/3