Слайд 1ЛЕКЦИЯ 1
Соответствия между множествами. Отображения и их виды
Слайд 2Задание:
1.Изучить новый материал в лекции
2. Записать конспект лекции
3. Выполнить тест.
Слайд 3 Основные понятия.
Пусть даны два множества А={а1, а2,...} и
В={b1, b2,...}. Тогда пары (ai, bj ) задают соответствие между
множествами А и В, если указано правило f, по которому для элемента ai множества А выбирается элемент bj из множества В.
Например, соответствие между элементами множеств и задает точечное множество (xi, yj ) координат точек на плоскости; русско-английский словарь устанавливает соответствие значений и написаний слов русского и английского языков.
Слайд 4
Пусть задано соответствие f между множествами А и В, т.
е. f:A→B, состоит из пар вида (a; b), где
Для
некоторого элемента а множества А поставлен в соответствие некоторый элемент b из множества B, который называется образом элемента а и записывается b = f(a).
Слайд 5
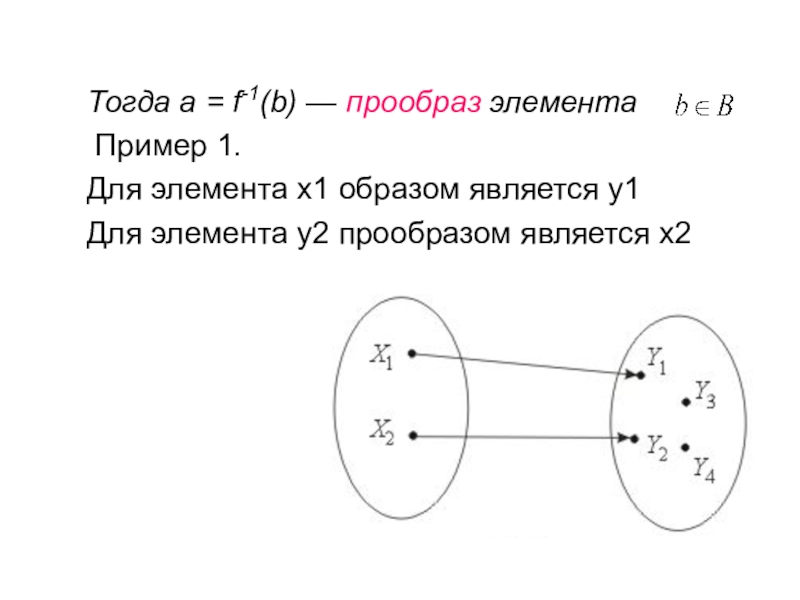
Тогда а = f-1(b) — прообраз элемента
Пример 1.
Для элемента
х1 образом является у1
Для элемента у2 прообразом является х2
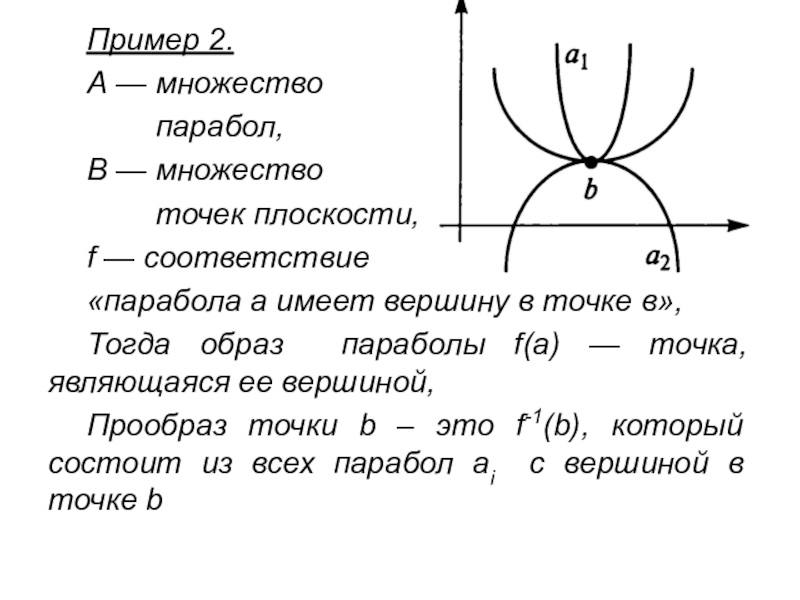
Слайд 6Пример 2.
А — множество
парабол,
В — множество
точек плоскости,
f
— соответствие
«парабола а имеет вершину в точке в»,
Тогда образ параболы f(a) — точка, являющаяся ее вершиной,
Прообраз точки b – это f-1(b), который состоит из всех парабол аi с вершиной в точке b
Слайд 7Образ множества А при соответствии f называется множеством значений этого
соответствия и обозначается f(A), если f(A) состоит из образов всех
элементов множества А. Запись:
Прообраз множества В при некотором соответствии f называют областью определения этого соответствия и обозначают f-1(B), т.е.
f-1 является обратным соответствием для f.
Слайд 8Отображение
Соответствие называется отображением, если для каждого элемента
найдется один и только один
его образ из множества В.
Соответствие,
но не отображение
Отображение
Слайд 9
Для описания соответствий между числовыми множествами используют понятие отображения
(функции) одного множества на другое.
Функцией f , действующей из
множества X в множество Y (f: X Y) называется правило или закон, по которому каждому элементу xX ставится в соответствие один и только один элемент yY.
Слайд 10 Задание отображений.
Для задания отображения необходимо указать:
• множество,
которое отображается (область определения данного отображения D(f));
• множество, в
(на) которое отображается данная область определения (множество значений этого отображения E(f));
• закон или соответствие между этими множествами, по которому для элементов первого множества (прообразов, аргументов) выбраны элементы (образы) из второго множества.
Приняты записи или f: A В.
Слайд 11Способы задания.
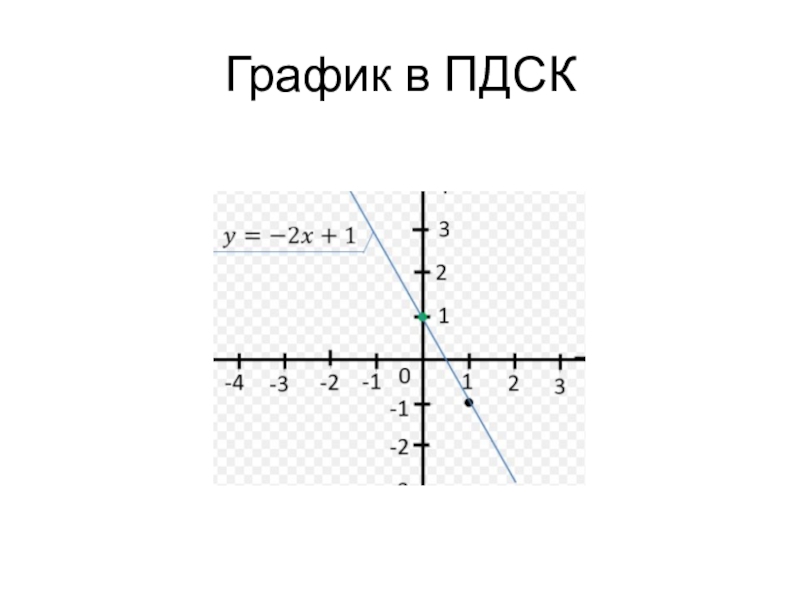
1. Способ задания отображений в виде формул называется аналитическим.
Например, у=2х-5.
2. Для задания отображения множеств табличным способом принято строить
таблицу, в которой первую строку составляют элементы области определения (прообразы вида а), а вторую строку — их образы, т. е. элементы вида (х) при отображении : а (а), где
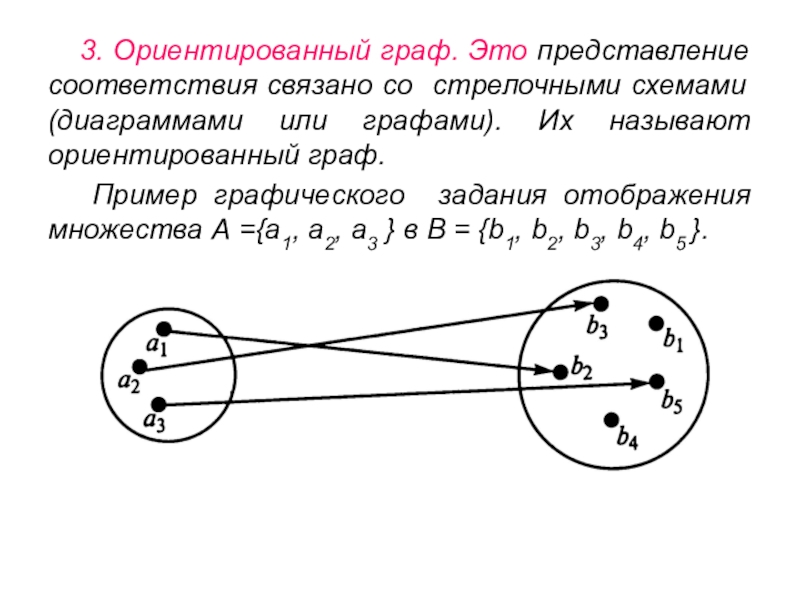
Слайд 123. Ориентированный граф. Это представление соответствия связано со стрелочными схемами
(диаграммами или графами). Их называют ориентированный граф.
Пример графического задания
отображения множества А ={а1, а2, а3 } в В = {b1, b2, b3, b4, b5 }.
Слайд 14Способы задания отображений
Перечислением пар
Словесным описанием
Таблица
Аналитический способ
Ориентированный граф
Графиком в ПДСК
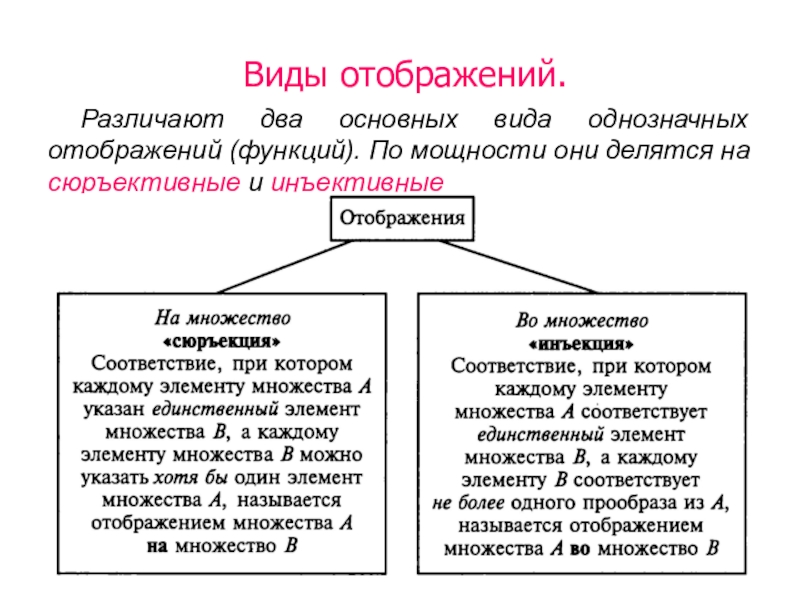
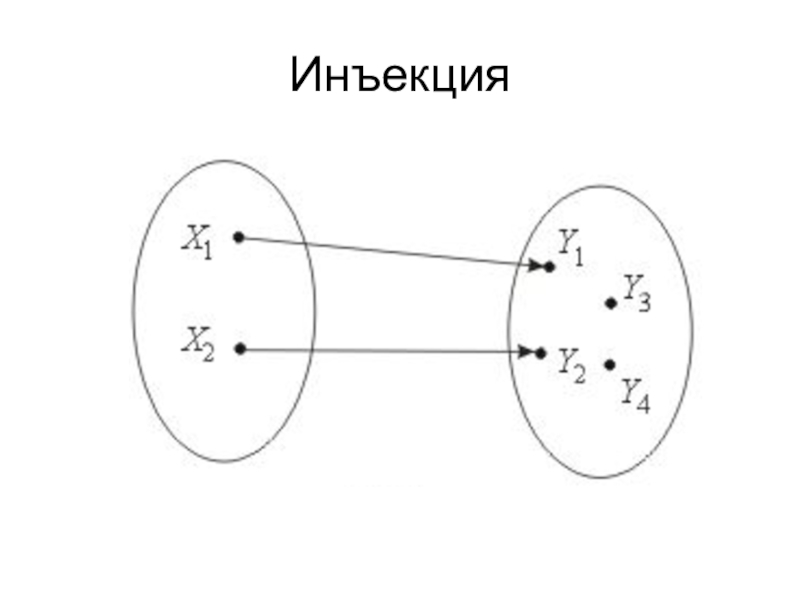
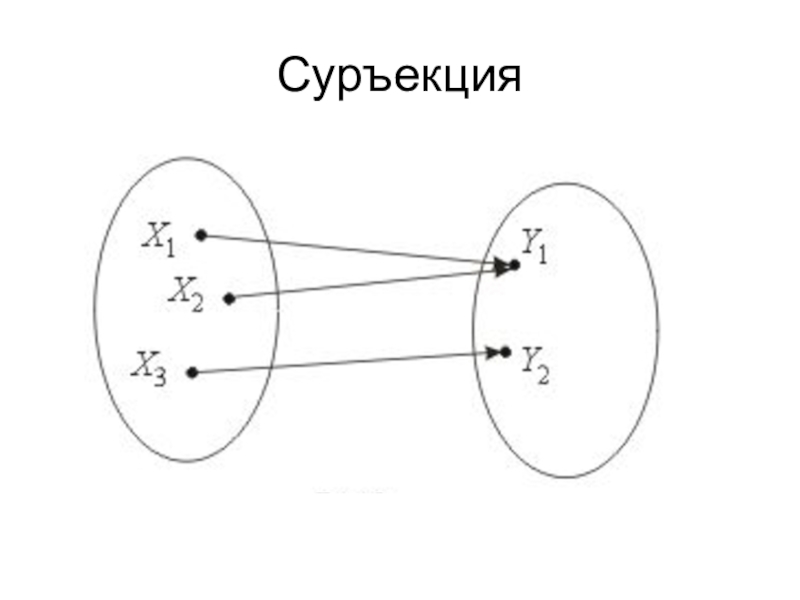
Слайд 15 Виды отображений.
Различают два основных вида однозначных отображений (функций).
По мощности они делятся на сюръективные и инъективные
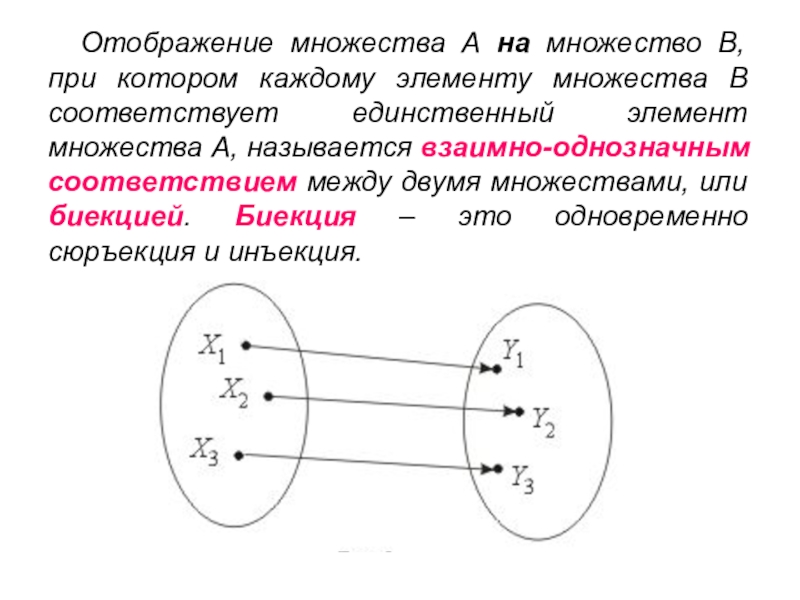
Слайд 18Отображение множества А на множество В, при котором каждому элементу
множества В соответствует единственный элемент множества А, называется взаимно-однозначным соответствием
между двумя множествами, или биекцией. Биекция – это одновременно сюръекция и инъекция.
Слайд 19 Два множества эквивалентны (равномощны), если между их элементами можно установить биективное
отображение.
Это обозначается следующим образом:
A ~ B.
Слайд 20Пусть множество А отображается взаимно-однозначно на множество В, т.е f:АВ.
Тогда отображение f -1, при котором каждому элементу множества В
ставится в соответствие его прообраз из множества А, называется обратным отображением для f и записывается
или f -1:ВА.
Так как одному образу при биекции соответствует в точности один прообраз, обратное отображение будет определено всюду на В и однозначно (отсюда название).
Для биекции принята запись:
Слайд 21
Если между элементами множеств установлено взаимно-однозначное соответствие, то эти множества
имеют одинаковое количество элементов.
Говорят, что они равночислены, равномощны, или
эквивалентны.
Слайд 22Рассмотрим примеры отображений.
1) Каждому действительному числу поставим в соответствие
его квадрат.
Отображение хх2 не является взаимно-однозначным соответствием, так как
для любого образа у=х2 можно найти два прообраза в области определения:
х = +у и х = -у.
Например, числа 3 и -3 имеют один и тот же квадрат число 9. Значит, это сюръекция.
Слайд 23Рассмотрим примеры отображений.
2) Англо-русский словарь устанавливает соответствие между множествами
слов английского и русского языков. Такое соответствие не является однозначным,
так как каждому английскому понятию соответствуют различные варианты перевода на русский язык (синонимы в русском языке, и наоборот. Это сюръекция.
Слайд 24Рассмотрим примеры отображений.
3) Различные виды кодирования (азбука Морзе, представление
чисел в различных системах счисления, шифрованные сообщения) являются чаще всего
примерами взаимно-однозначного соответствия между множествами. Каждой букве и цифре соответствует одна комбинация точек и тире в азбуке Морзе.
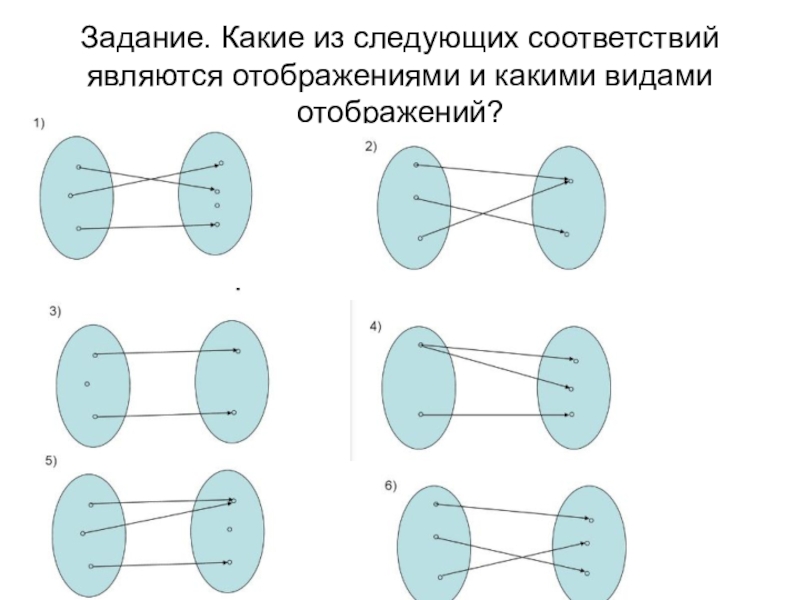
Слайд 25Задание. Какие из следующих соответствий являются отображениями и какими видами
отображений?