Слайд 1Лекция 24
1 декабря 2009 года
Тема: Структуры данных. Деревья.
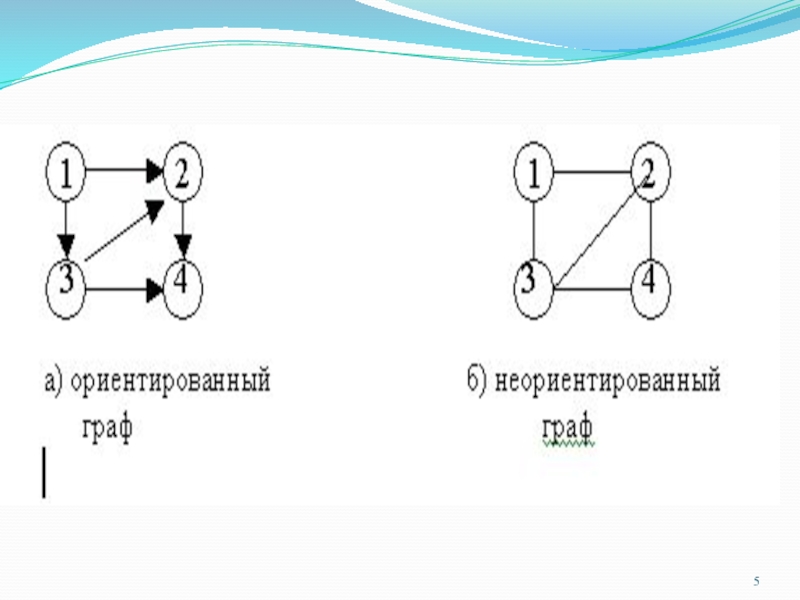
Слайд 2Определение графа
Неориентированный граф G — это упорядоченная пара G = (V,E),
где
V – конечное множество вершин или узлов;
E - множество неупорядоченных
пар различных вершин, называемых рёбрами.
Вершины u и v называются концевыми вершинами ребра e = (u,v).
Два ребра называются смежными, если они имеют общую концевую вершину.
Если пары множества E упорядочены, то граф является ориентированным, а элементы множества E – дугами.
Слайд 3 В неориентированном графе (v,w)=(w,v).
Путь – это последовательность ребер вида (v1,v2),
(v3,v4),…, (vn-1,vn).
Говорят, что этот путь идет из вершины v1
в вершину vn и имеет длину n-1. Часто его обозначают как последовательность вершин v1,v2,v3,v4,…, vn-1,vn.
Тогда -
Путь - конечная последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.
Слайд 4Путь называется простым, если все ребра и все узлы на
нем , кроме, может быть, первого и последнего, различны.
Слайд 6Определение дерева
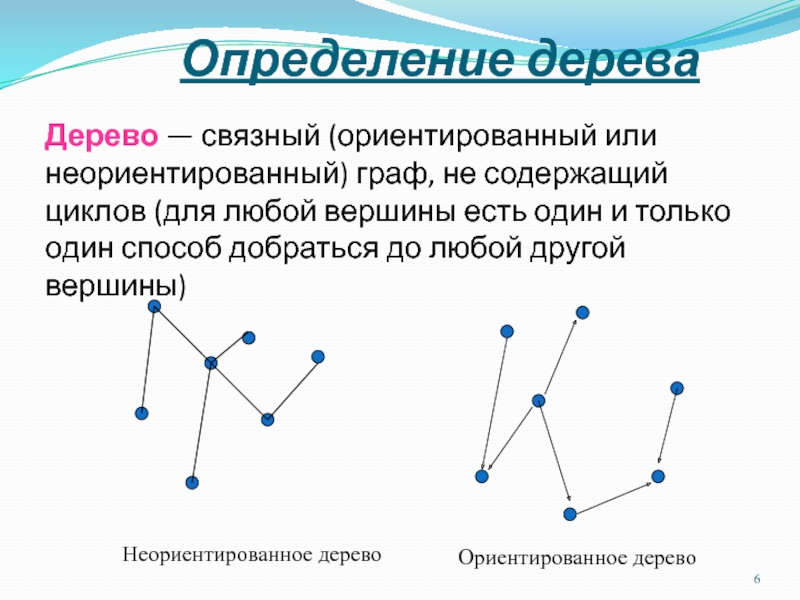
Дерево — связный (ориентированный или неориентированный) граф, не содержащий
циклов (для любой вершины есть один и только один способ
добраться до любой другой вершины)
Неориентированное дерево
Ориентированное дерево
Слайд 7Корневое дерево
Корневое дерево определяется как конечное множество T одного или
более узлов со следующими свойствами:
существует один корень дерева T ;
остальные
узлы (за исключением корня) распределены среди непересекаю-щихся множеств T1,...,Tm, и каждое из множеств является деревом; деревья T1,...,Tm называются поддеревьями корня T
Слайд 8Определения, связанные с деревьями
Степень узла — количество поддеревьев узла.
Концевой узел (лист) —
узел со степенью нуль.
Уровень узла определяется следующим образом:
-
уровень корня дерева T равен нулю;
- уровень корней поддеревьев любой вершины дерева на единицу больше, чем уровень этой вершины.
Высота дерева – максимальное значение уровня какой-либо вершины дерева
Слайд 9Глубина узла v в дереве – длина пути из корня
в v.
Высота узла v в дереве – это длина самого
длинного пути из v в какой-нибудь лист.
Высота дерева – это высота его корня.
Уровень узла равен разности высоты дерева и глубины узла.
Упорядоченным называется дерево, в котором множество сыновей каждого узла упорядочено.
При описании деревьев могут быть использованы термины из ботаники («корень», «лист», «ветвь»), либо из генеалогии («отец», «сын», «предок», «потомок», «брат»).
Слайд 10Лес — множество (обычно упорядочен-ное), не содержащее ни одного непересе-кающегося дерева
или содержащее несколько непересекающихся деревьев.
Ориентированное дерево — это ориентированный граф
без циклов, в котором в каждую вершину, кроме одной, называемой корнем ориентированного дерева, входит одно ребро. В корень ориентированного дерева не входит ни одного ребра. Иногда, термин «ориентированное дерево» сокращают до «дерева».
Слайд 11 Дерево – это ориентированный граф без циклов, удовлетворяющий следующим условиям:
Имеется
в точности один узел, называемый корнем, в который не входит
ни одно ребро;
В каждый узел, кроме корня входит ровно одно ребро;
Из корня к каждому узлу идет путь (единственный).
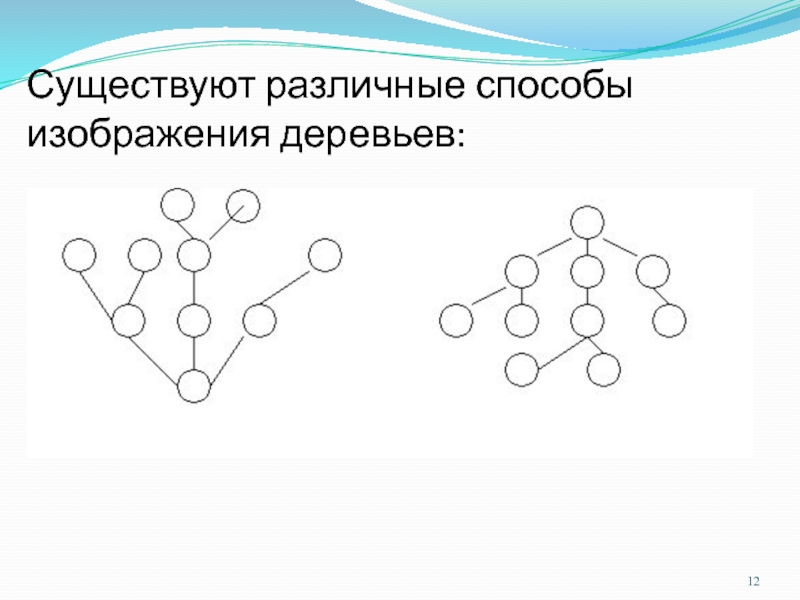
Слайд 12
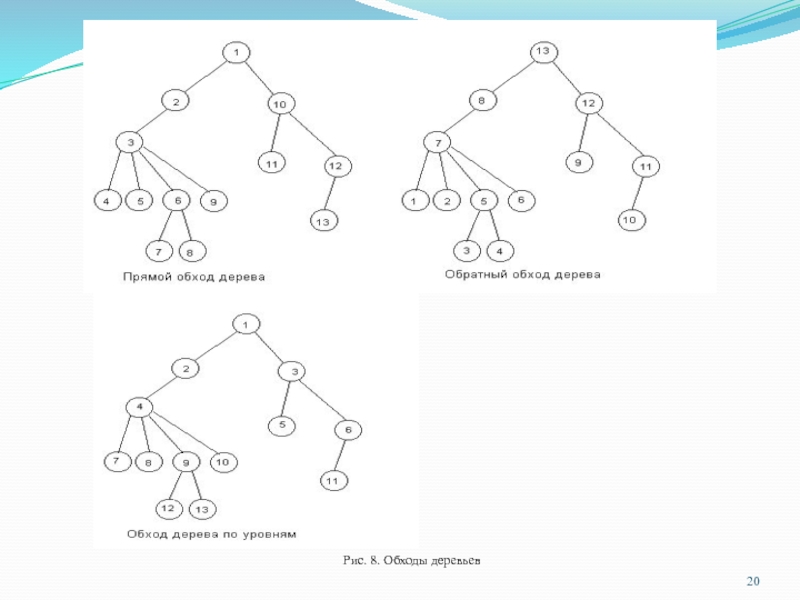
Существуют различные способы изображения деревьев:
Слайд 13Обходы деревьев
Обход дерева – операция, связанная с посещением его вершин
(под посещением понимается любая операция над вершиной дерева, не затрагивающая
структуру дерева)
При обходе каждая вершина должна быть посещена ровно один раз
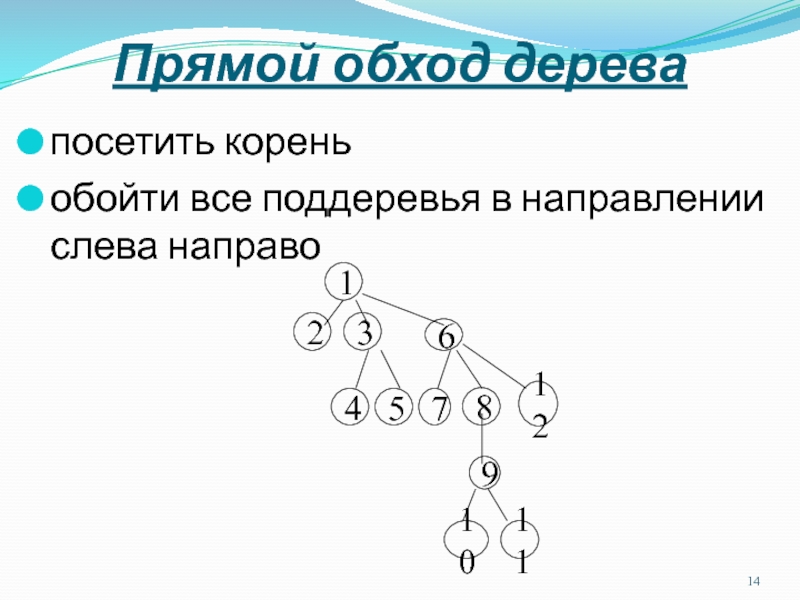
Слайд 14Прямой обход дерева
посетить корень
обойти все поддеревья в направлении слева направо
1
2
3
6
4
5
7
8
12
9
10
11
Слайд 15Прямой обход (просмотр в глубину, просмотр сверху–вниз) определяется следующим рекурсивным
алгоритмом:
посетить корень
обойти все поддеревья корня, начиная с самого левого
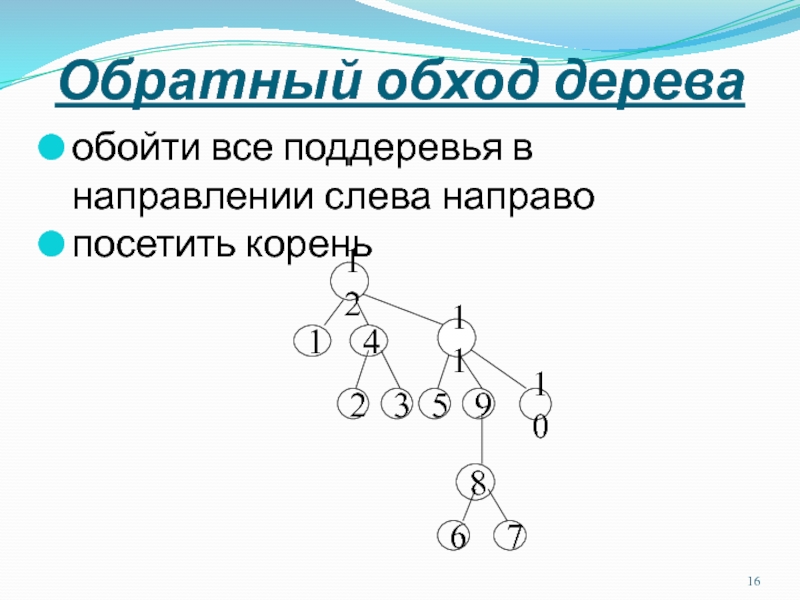
Слайд 16Обратный обход дерева
обойти все поддеревья в направлении слева направо
посетить корень
12
1
4
2
3
5
9
10
8
6
7
11
Слайд 17 Обратный обход (просмотр снизу–вверх) дерева определяется следующим рекурсивным алгоритмом:
обойти
все поддеревья корня, начиная с самого левого
посетить корень
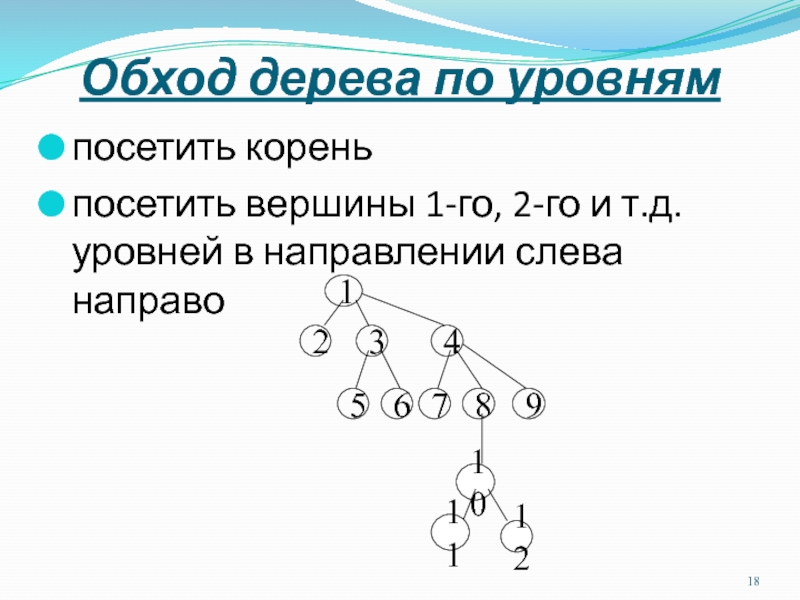
Слайд 18Обход дерева по уровням
посетить корень
посетить вершины 1-го, 2-го и т.д.
уровней в направлении слева направо
1
2
3
4
5
6
7
8
9
10
11
12
Слайд 19Обход деревьев по уровням :
Вначале посещается корень дерева, затем
– его сыновья, начиная с самого левого, затем – внуки.
Так продолжается до тех пор, пока все вершины не посещены.
Слайд 21
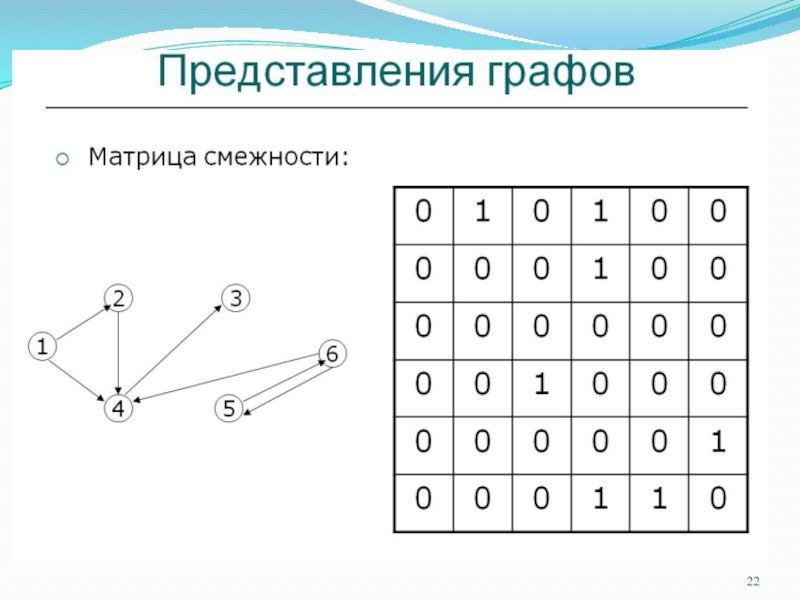
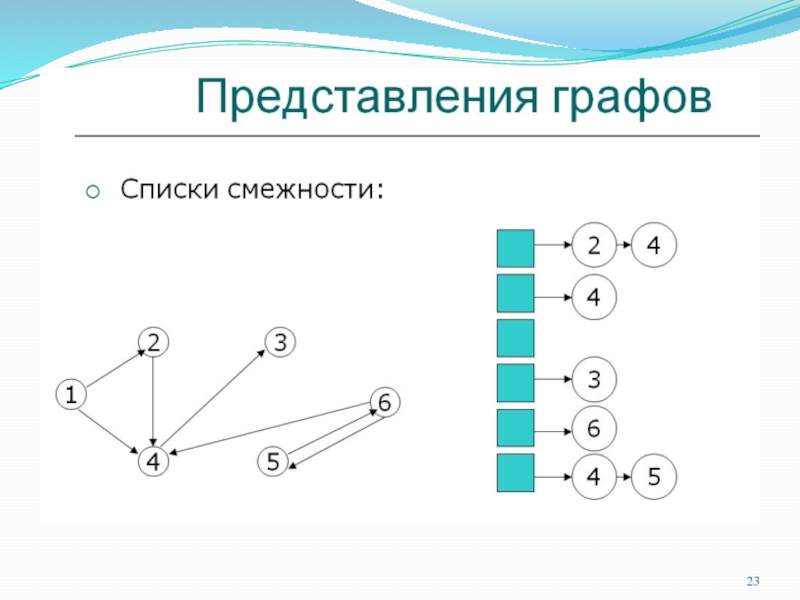
Представление деревьев
Физическая реализация деревьев может быть выполнена различными способами.
1.
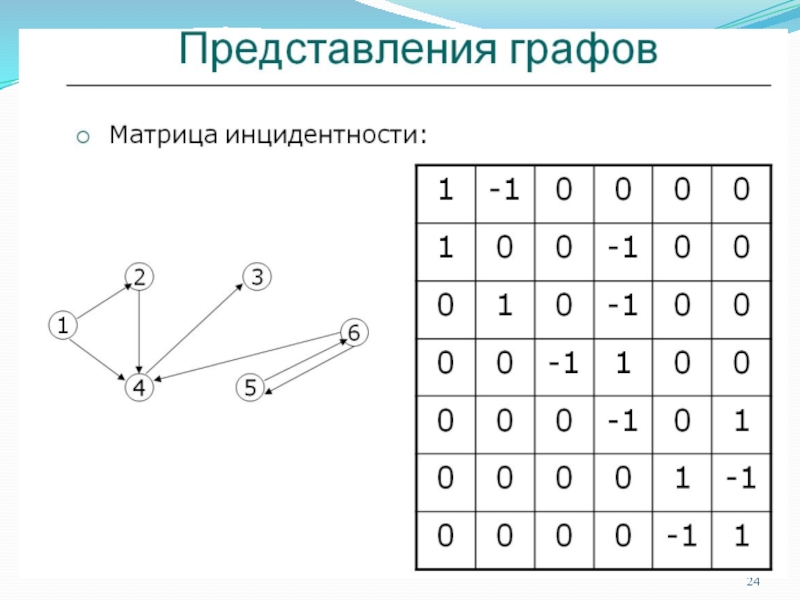
Поскольку деревья являются частным случаем понятия графа, то для них
можно применить любое представление, разработанное для графа общего вида (например, матрицу смежности или матрицу инцидентности).
Слайд 25 2. Существуют представления, ориентированные на деревья. Наиболее простым и понятным
из них является т.н. каноническое представление дерева, когда каждая вершина
содержит ссылку на своего отца (корень, естественно, содержит пустую ссылку).
Такое представление удобно, когда надо представить не одно дерево, а лес из нескольких деревьев. Но операций, которые удобно выполнять с помощью такого представления, не слишком много. Так, можно легко определить предков каждой вершины, но не ее потомков. Кроме того, модификация дерева затруднена при этом представлении.
Слайд 26
3. Следующее представление дерева заключается в том, что каждая его
вершина содержит список ссылок на сыновей этой вершины. Теперь можно
легко выполнить поиск всех потомков конкретной вершины (но не ее предков!).
Слайд 27 Часто два последних представления комбинируют, получая нечто вроде двунаправленного списка.
Хотя полученная структура и является несколько избыточной, она позволяет легко
проходить дерево в обоих направлениях: от листьев к корням и обратно.
Рассмотрим конкретную реализацию этого представления на примере бинарных деревьев.
Слайд 28Двоичные деревья
Двоичное (бинарное) дерево (ориентированное) — это ориентированное дерево, в
котором исходящие степени вершин (число исходящих рёбер) не превосходят 2.
На
двоичном дереве основаны следующие структуры данных:
двоичное дерево поиска
двоичная куча
красно-чёрное дерево
АВЛ-дерево
Фибоначчиева куча
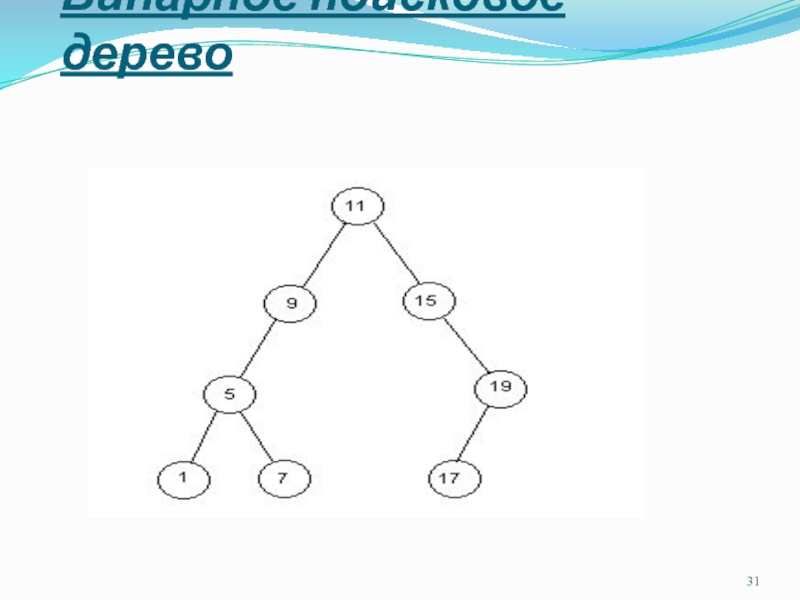
Слайд 29Двоичное дерево поиска
Двоичное дерево поиска (бинарное поисковое дерево, БПД) –
структура данных, предназначенная для выполнения следующих операций:
поиска элемента по значению
добавления
нового элемента
удаления элемента из дерева
Слайд 30Структура БПД
Сыновья каждой вершины различаются: выделяются левый и правый сын
Значения
хранятся в каждой вершине дерева
Для любого узла значения в левом
поддереве меньше, а значения в правом поддереве – больше значения, хранящегося в корне
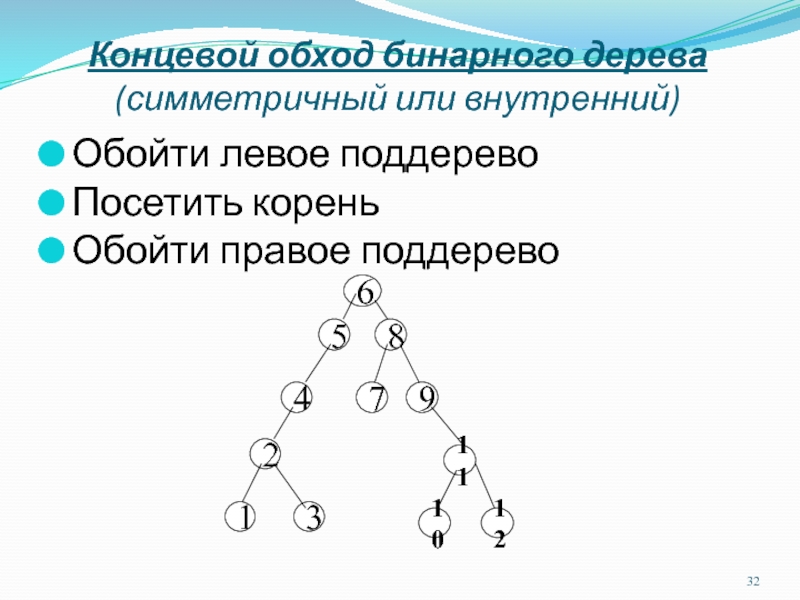
Слайд 32Концевой обход бинарного дерева (симметричный или внутренний)
Обойти левое поддерево
Посетить корень
Обойти
правое поддерево
6
5
8
7
9
11
12
10
4
2
1
3
Слайд 33Механизм поиска в БПД
Если дерево пусто, то поиск завершился неудачно.
В противном случае сравниваем искомое значение со значением корня. Если
эти значения равны, то искомое значение найдено; иначе рекурсивно выполняем эту же процедуру для левого или правого поддерева, в зависимости оттого, что больше – значение корня или искомое значение.
Слайд 34 Поиск в БПД требует в лучшем случае О(log n) операций
сравнения, где n – число элементов.
Однако, если дерево не
сбалансировано (т.е. длина одной из ветвей существенно больше длины другой), то эффективность поиска снижается и в худшем случае может достичь О(n) операций, когда дерево вырождается в единственную ветвь.
Слайд 35Поиск значения в БПД
Пусть K – искомое значение, T –
значение в корне дерева
if (K==T) поиск завершен успешно
else if
(K if (есть левый сын)
выполнить поиск в левом поддереве
else
поиск завершен неудачно
else
if (есть правый сын)
выполнить поиск в правом поддереве
else
поиск завершен неудачно
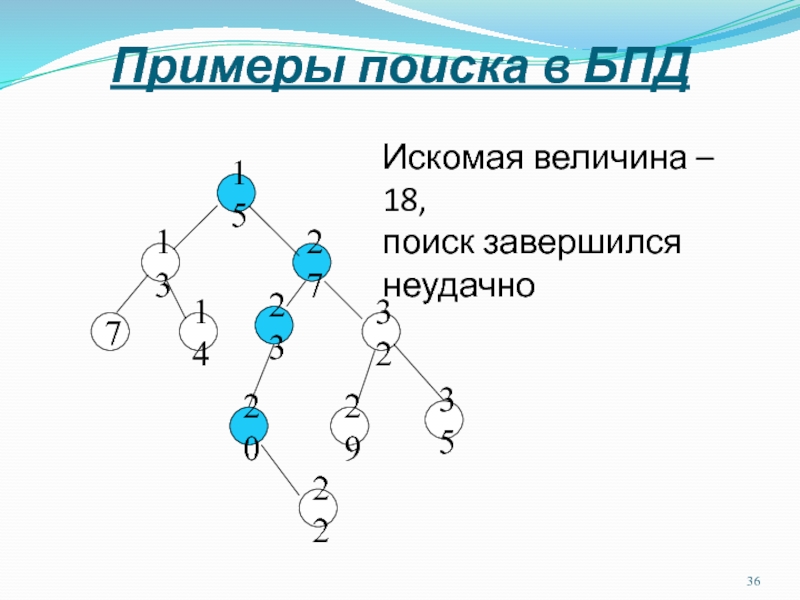
Слайд 36Примеры поиска в БПД
15
27
23
20
32
35
7
14
13
22
29
Искомая величина – 18,
поиск завершился неудачно
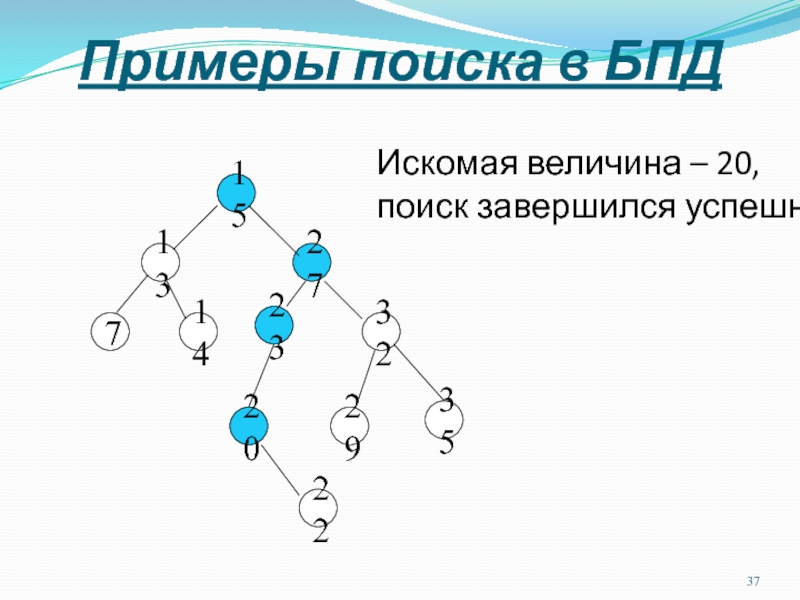
Слайд 37Примеры поиска в БПД
15
27
23
20
32
35
7
14
13
22
29
Искомая величина – 20,
поиск завершился успешно
Слайд 38Вставка новой вершины в БПД
если БПД пусто, создаем единственную вершину
и делаем ее корнем;
иначе выполняем поиск вершины с добавляемым значением;
если
поиск успешен, вставка невозможна;
в противном случае добавляем новую вершину и делаем ее сыном (левым или правым) той вершины, на которой остановились в процессе поиска
Слайд 39Пример создания БПД последовательностью вставок
Добавляемые элементы: 7, 19, 14, 3,
5, 8, 22, 9, 1, 20, 2
7
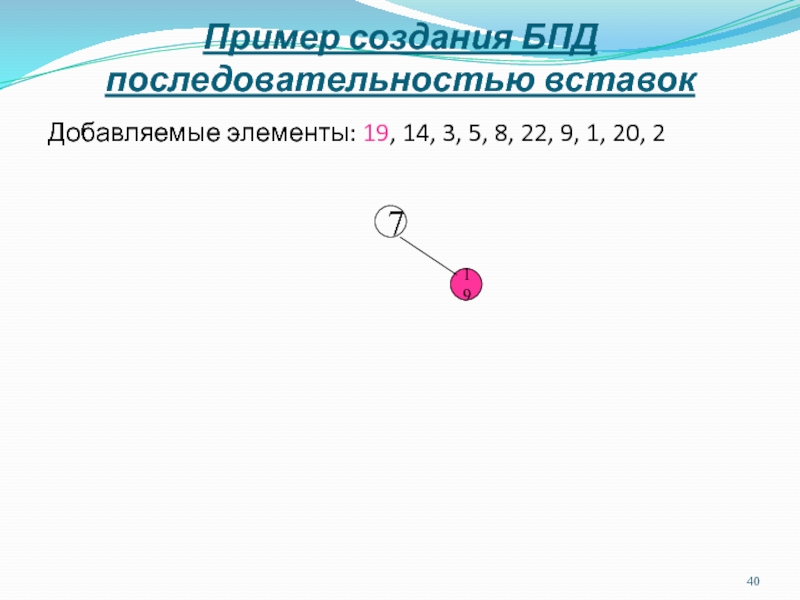
Слайд 40Пример создания БПД последовательностью вставок
Добавляемые элементы: 19, 14, 3, 5,
8, 22, 9, 1, 20, 2
7
19
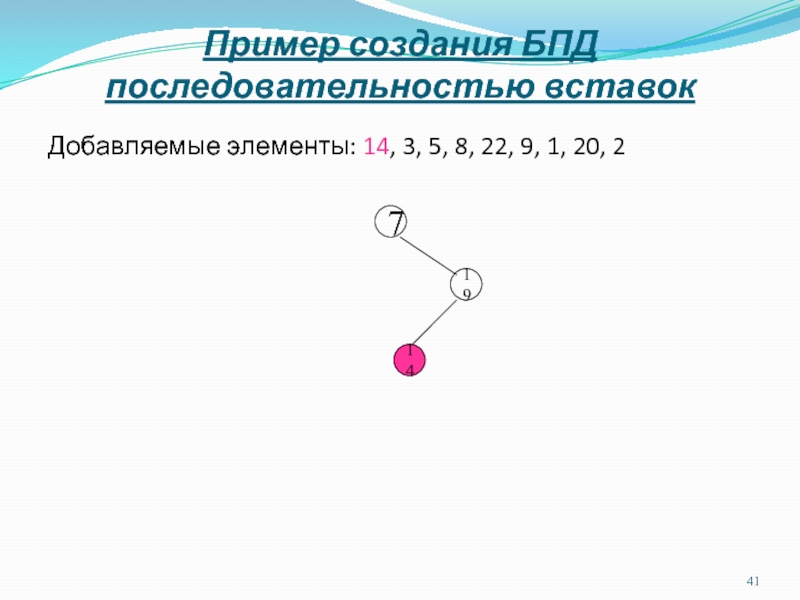
Слайд 41Пример создания БПД последовательностью вставок
Добавляемые элементы: 14, 3, 5, 8,
22, 9, 1, 20, 2
7
19
14
Слайд 42Пример создания БПД последовательностью вставок
Добавляемые элементы: 3, 5, 8, 22,
9, 1, 20, 2
7
19
14
3
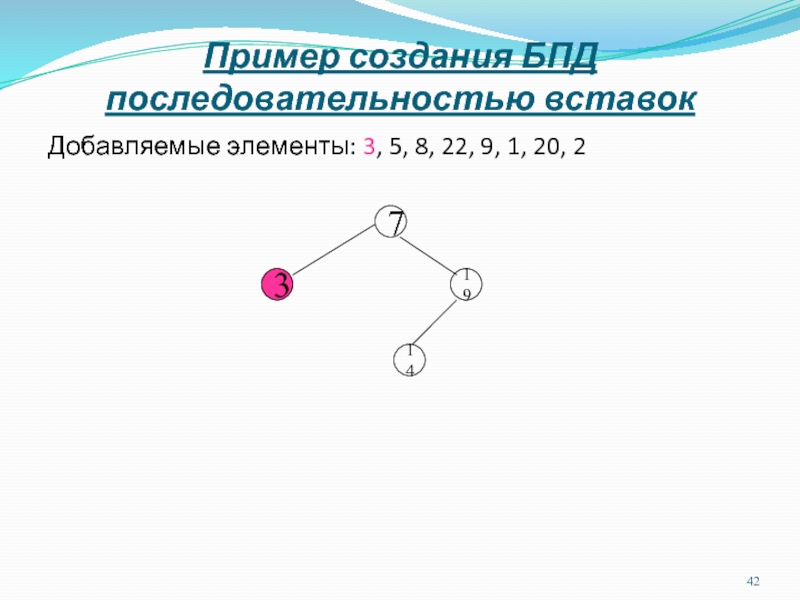
Слайд 43Пример создания БПД последовательностью вставок
Добавляемые элементы: 5, 8, 22, 9,
1, 20, 2
7
19
14
3
5
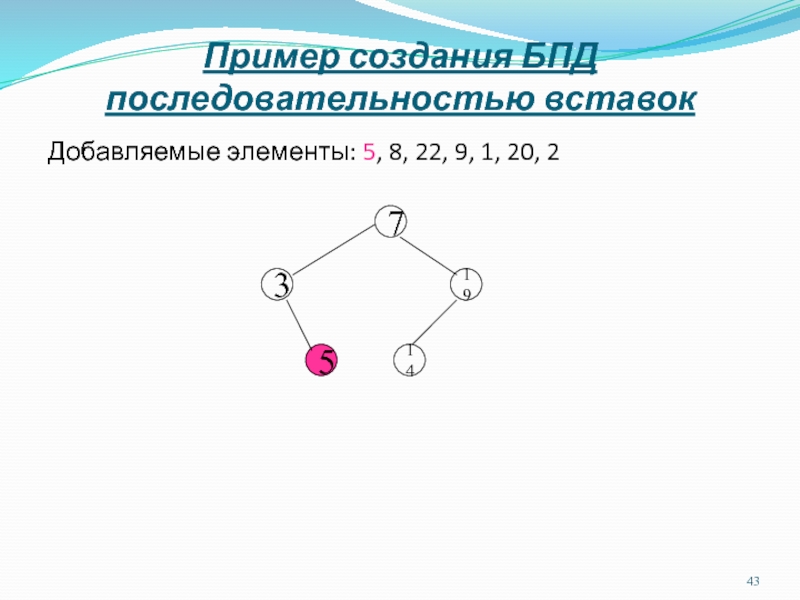
Слайд 44Пример создания БПД последовательностью вставок
Добавляемые элементы: 8, 22, 9, 1,
20, 2
7
19
14
3
5
8
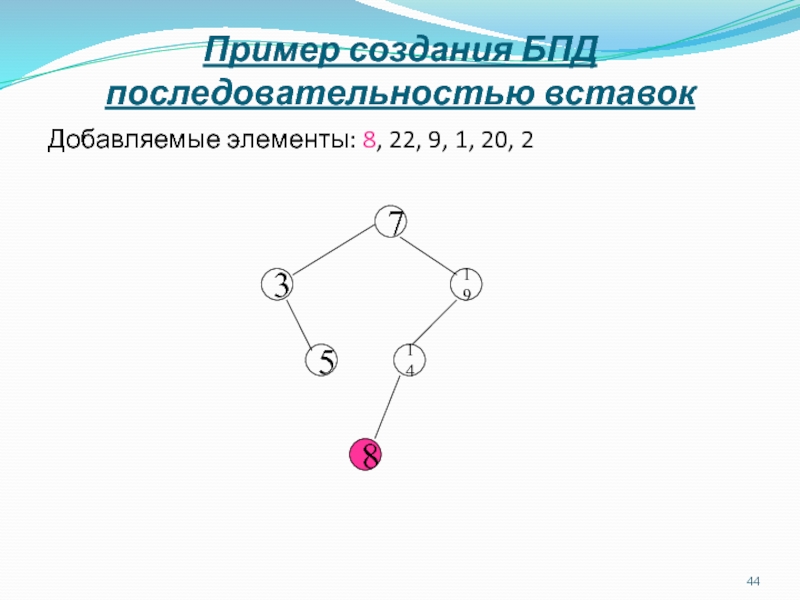
Слайд 45Пример создания БПД последовательностью вставок
Добавляемые элементы: 22, 9, 1, 20,
2
7
19
14
3
5
8
22
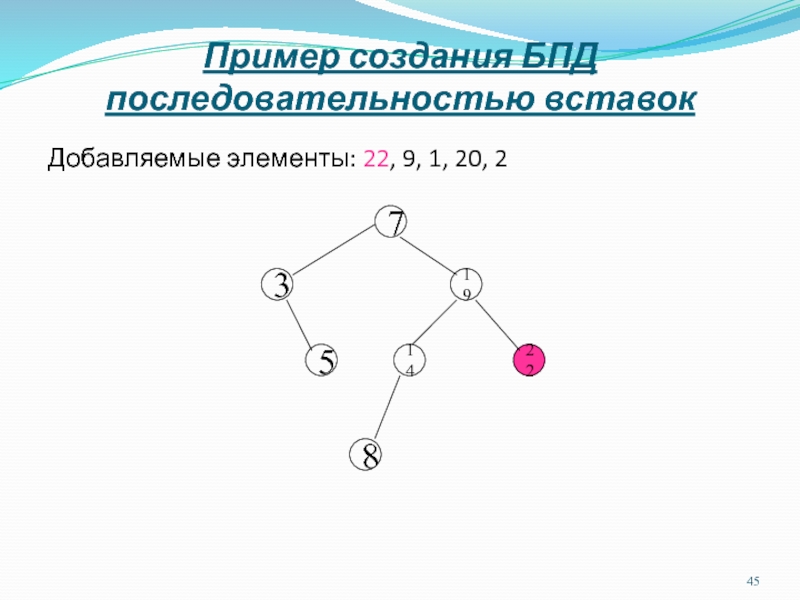
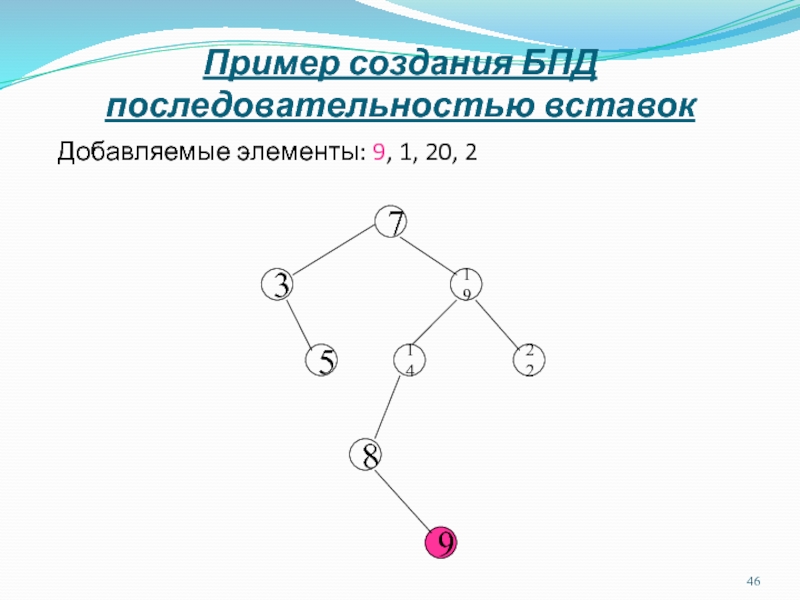
Слайд 46Пример создания БПД последовательностью вставок
Добавляемые элементы: 9, 1, 20, 2
7
19
14
3
5
8
22
9
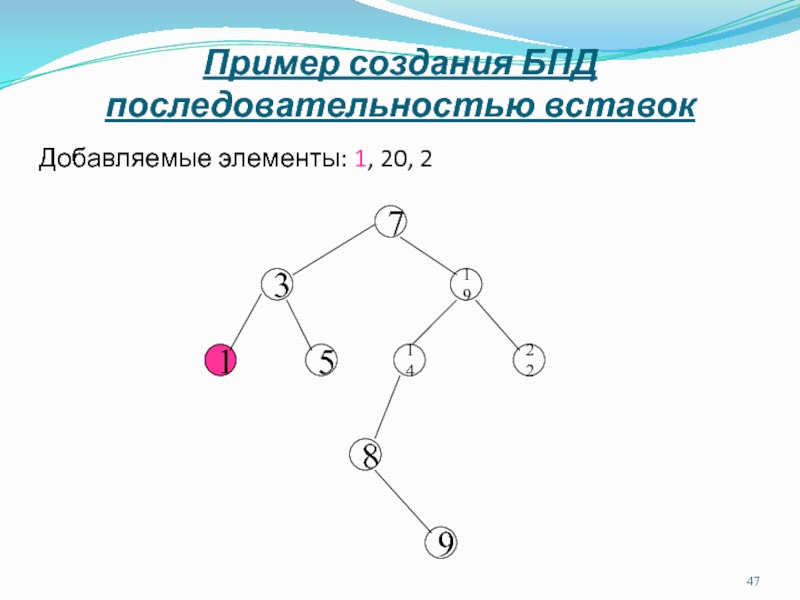
Слайд 47Пример создания БПД последовательностью вставок
Добавляемые элементы: 1, 20, 2
7
19
14
3
5
8
22
9
1
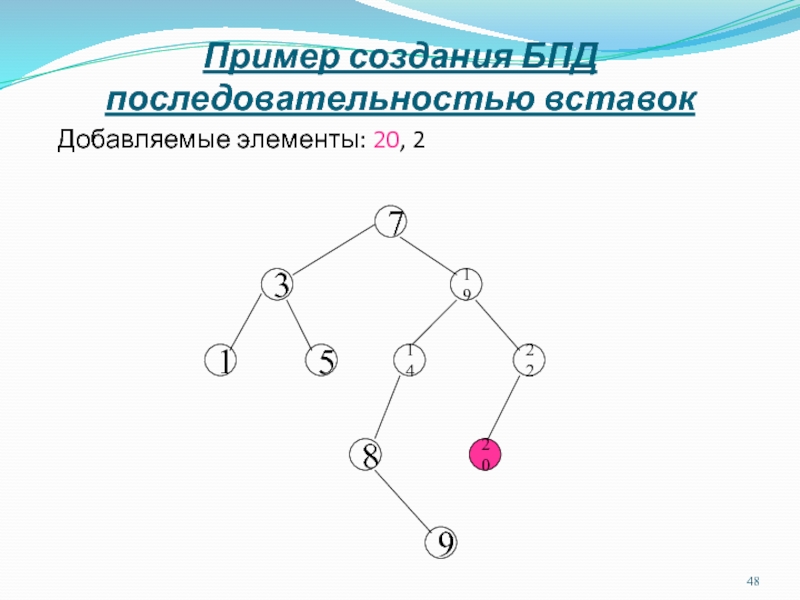
Слайд 48Пример создания БПД последовательностью вставок
Добавляемые элементы: 20, 2
7
19
14
3
5
8
22
9
1
20
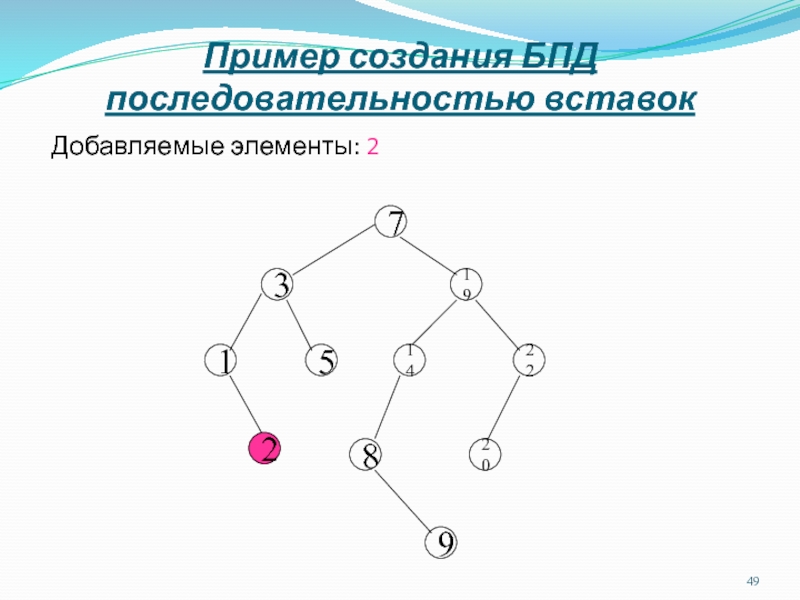
Слайд 49Пример создания БПД последовательностью вставок
Добавляемые элементы: 2
7
19
14
3
5
8
22
9
1
20
2
Слайд 50Проблемы балансировки
9
15
11
25
28
20
17
19
Слайд 54Физическая реализация БПД
Наиболее удобной реализацией БПД представляется задание каждой
его вершины в динамической памяти. В статическую область помещается лишь
указатель на корень дерева:
Слайд 55struct TreeItem{
int Info;
TreeItem* Father;
TreeItem* LSon;
TreeItem* RSon;
TreeItem(){LSon=RSon=NULL}
};
TreeItem* Root = NULL;
//
пустое дерево
Слайд 56bool find(int a, TreeItem* &t) // поиск элемента
{ if (Root ==
NULL)
{ t = NULL;
return false;
}
t = Root;
for (;;)
{ if (t->Info == a)
return true;
if (t->Info > a)
{ if (t->LSon == NULL) return false;
t = t->LSon;
}
else
{ if (t->RSon == NULL) return false;
t = t->RSon;
}
}
}
Слайд 57bool Insert(int info)
// добавление нового элемента в дерево
{ TreeItem *s,*q;
if
(find(info,s)) return false;
q = new TreeItem;
q->Info = info;
if (s ==
NULL)
{ Root = q;
q->Father = NULL;
}
else
{ q->Father = s;
if (s->Info < info)
s->RSon = q;
else s->LSon = q;
}
return true;
}
STOP
Слайд 59 Для уничтожения дерева концевой обход применить нельзя, т.к. посещение вершины
приведет к ее удалению, и понятие «правое поддерево» станет неопределенным.
Поэтому применяется обратный обход:
Слайд 60procedure Destroy(var T: TTree); {уничтожение дерева}
procedure Round1(var N: PTreeNode);
begin
if N=nil then
exit;
Round1(N^.LSon);
Round1(N^.RSon);
dispose(N);
end; {Round1}
begin
Round1(T.Root);
T.Root := nil;
end;
Слайд 61function Find(T: TTree; AInfo: TInfo;
var N:
PTreeNode): boolean;
{при удачном поиске функция возвращает true, а параметр
N содержит указатель на найденную вершину;
при неудачном поиске функция возвращает false, а параметр N содержит указатель на вершину, на которой завершился поиск;
при попытке поиска в пустом дереве параметр N содержит nil}
var
P: PTreeNode;
Слайд 62begin
N := nil; P := T.Root;
while true do
begin
if P=nil then
begin
Find := false; exit; end;
N := P;
if P^.Info = AInfo then
begin Find := true; exit; end;
if P^.Info > AInfo then P := P^.LSon
else P := P^.RSon;
end;
end;
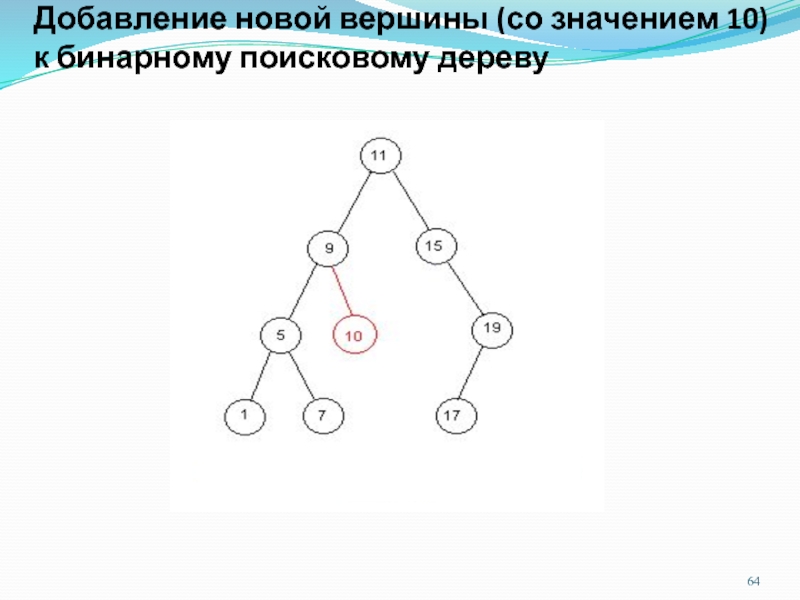
Слайд 63Вставка и удаление вершин в БПД
Очевидно, что вставляемая в
БПД вершина будет являться листом и может быть добавлена только
в одно конкретное место дерева (если мы, конечно, не желаем выполнить полное перестроение дерева).
Слайд 64Добавление новой вершины (со значением 10) к бинарному поисковому дереву
Слайд 65function Insert(var T: TTree; AInfo: TInfo): boolean;
{вставка элемента по
значению в бинарное поисковое дерево;
функция возвращает false при обнаружении
дубликата}
var
N, P: PTreeNode;
Слайд 66begin
if Find(T, AInfo, N) then
begin {нашли дубликат}
Insert := false;
exit;
end;
Insert := true;
new(P);
P^.Info := AInfo;
P^.RSon := nil;
P^.LSon := nil;
Слайд 67if N=nil then
begin{вставка первого эл-та в пустое
дерево}
T.Root := P;
P^.Father := nil;
end
else
begin
P^.Father := N;
if N^.Info
N^.RSon := P
else
N^.LSon := P;
end;
end;
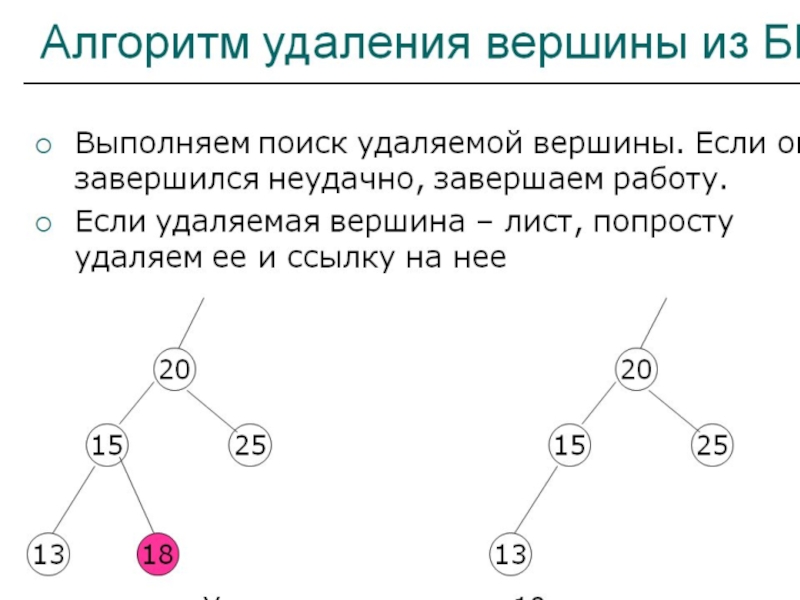
Слайд 68Удаление вершины из БПД
Выполняется немного сложнее и состоит из 2-х
этапов:
· поиск вершины;
· удаление.
Слайд 69 Возможны три варианта в зависимости от того, сколько сыновей имеет
удаляемая вершина (ни одного, одного, двух):
a)Вершина не имеет сыновей, т.е.
является листом. Тогда просто удаляется ссылка на эту вершину;
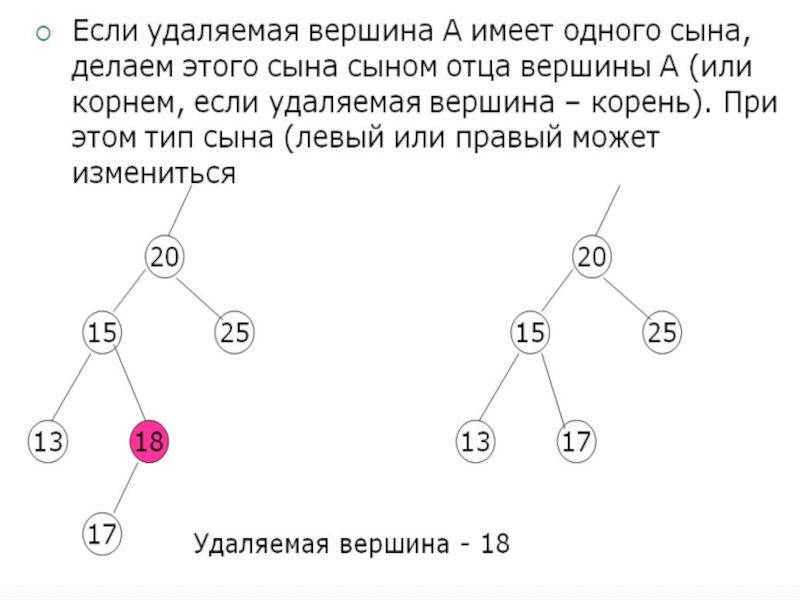
b)Вершина имеет одного сына, действия по удалению очевидны;
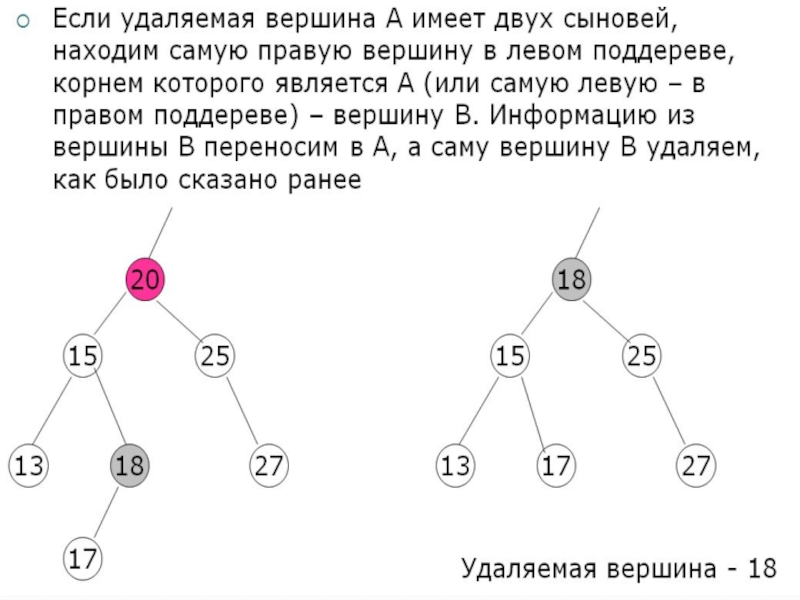
c)Удаляемая вершина (обозначим S) имеет двух сыновей.
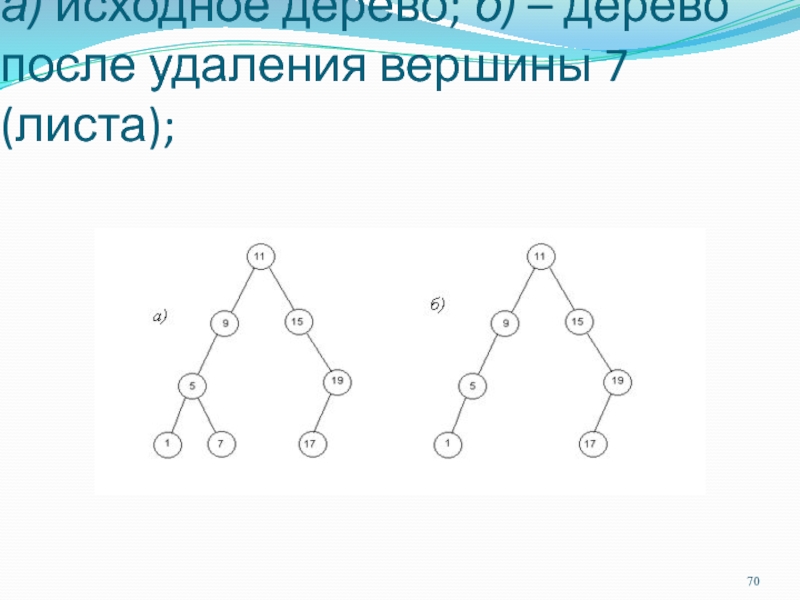
Слайд 70а) исходное дерево; б) – дерево после удаления вершины 7
(листа);
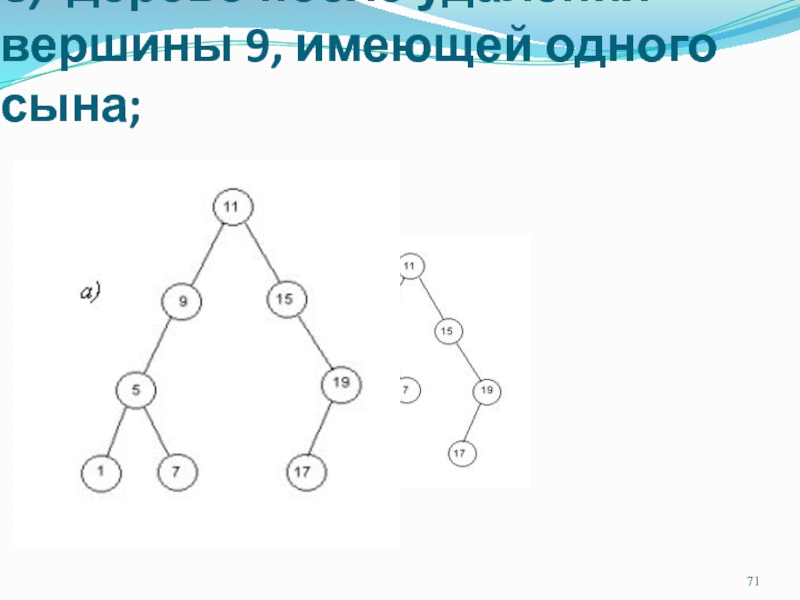
Слайд 71в) дерево после удаления вершины 9, имеющей одного сына;
Слайд 72 В случае (c) нужно найти такую вершину, чтобы ее удобно
было переместить на место удаляемой. Чтобы найти такую вершину необходимо
идти по дереву от исключаемого звена один раз налево и потом все время вправо (или наоборот), т.е. найти самую левую вершину в правом поддереве или самую правую вершину в левом поддереве, корнем которого является S.
Слайд 73 Обозначим найденную вершину через T. Тогда для удаления
вершины S необходимо:
· перенести в нее содержимое информационной части
вершины T;
· удалить вершину T (поскольку она имеет не более одного сына, это действие особых проблем не вызывает).
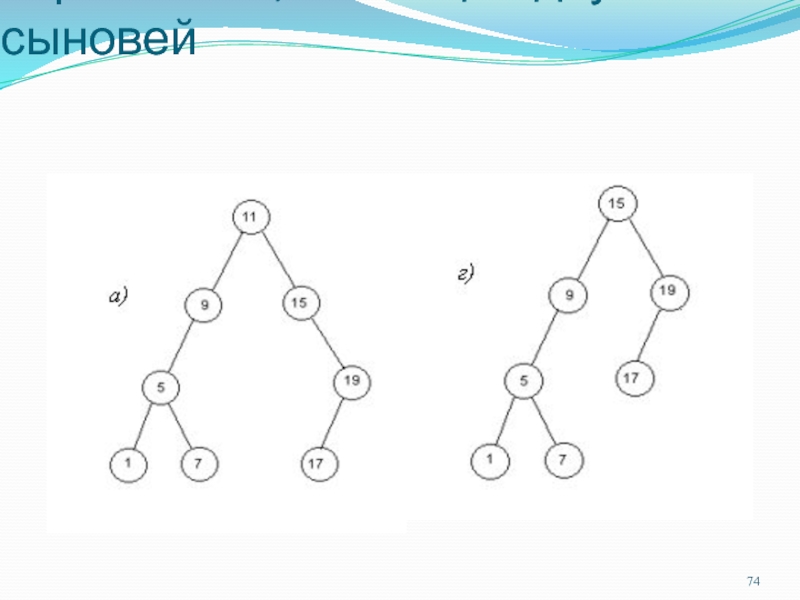
Слайд 74г) дерево после удаления вершины 11, имеющей двух сыновей
Слайд 75function Delete(var T: TTree;
AInfo: TInfo): boolean;
{удаление элемента по
значению из бинарного поискового дерева;
функция возвращает false при неудачном
удалении}
var
N, P: PTreeNode;
Слайд 76procedure DeleteNode(P: PTreeNode);
{удаление вершины, имеющей не более одного
сына}
var
Q: PTreeNode;
Слайд 77begin
if P^.LSon nil then Q := P^.LSon
else
Q := P^.RSon;
if Q nil then
Q^.Father
:= P^.Father;
if P^.Father = nil then
T.Root := Q
else
if (P^.Father)^.LSon = P then
(P^.Father)^.LSon := Q
else
(P^.Father)^.RSon := Q;
dispose(P);
end; {DeleteNode}
Слайд 78begin
if not Find(T, AInfo, N) then
begin
{не нашли удаляемый элемент}
Delete := false; exit;
end;
Delete := true;
if (N^.LSon<>nil)and(N^.RSon<>nil) then
begin
P := N^.RSon;
while P^.LSon <> nil do
P := P^.LSon;
N^.Info := P^.Info; DeleteNode(P);
end
else DeleteNode(N);
end;