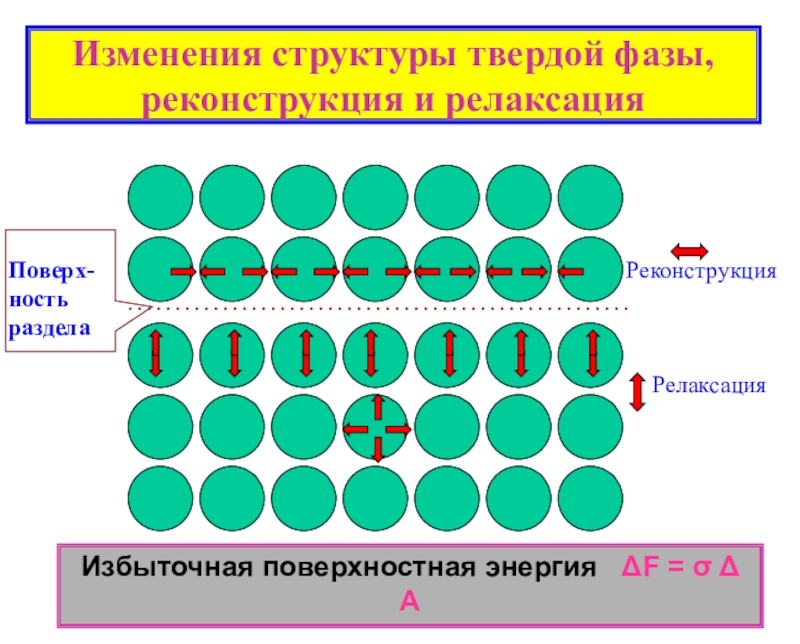
поверхности раздела сопредельных фаз.
-Миграция адсорбированных молекул по поверхности.
-Классические
теоретические уравнения изотерм адсорбции Генри, Ленгмюра, Фаулера- Гугенгейма, БЭТ и др. -Оценка площадок, занимаемых адсорбиро-ванными молекулами в заполненном монослое.





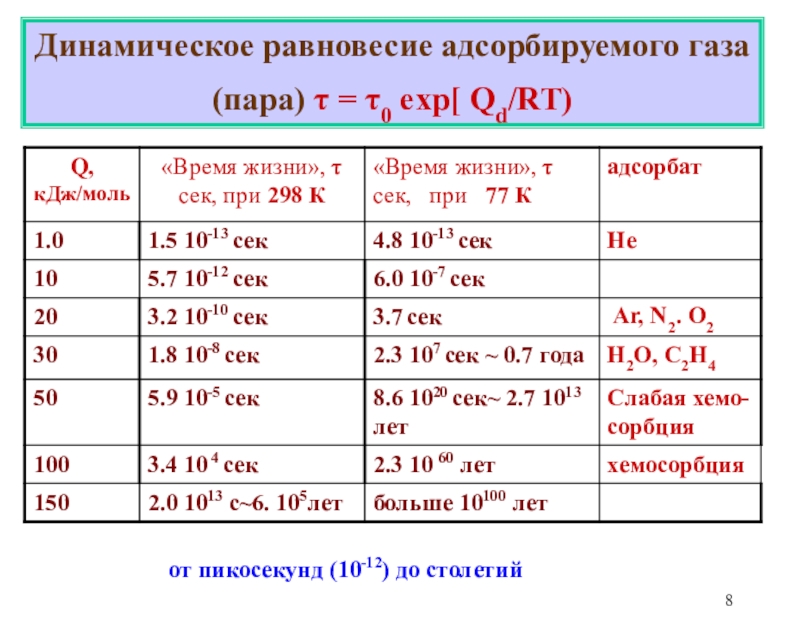








![Лекция 2 Динамический характер адсорбции А + [Z] [AZ] константа скоростиРА (1- ) А + [Z] [AZ] константа скоростиРА (1- )](/img/tmb/6/508005/edc3bbfd4df4653da7a79727c8f658d9-800x.jpg)

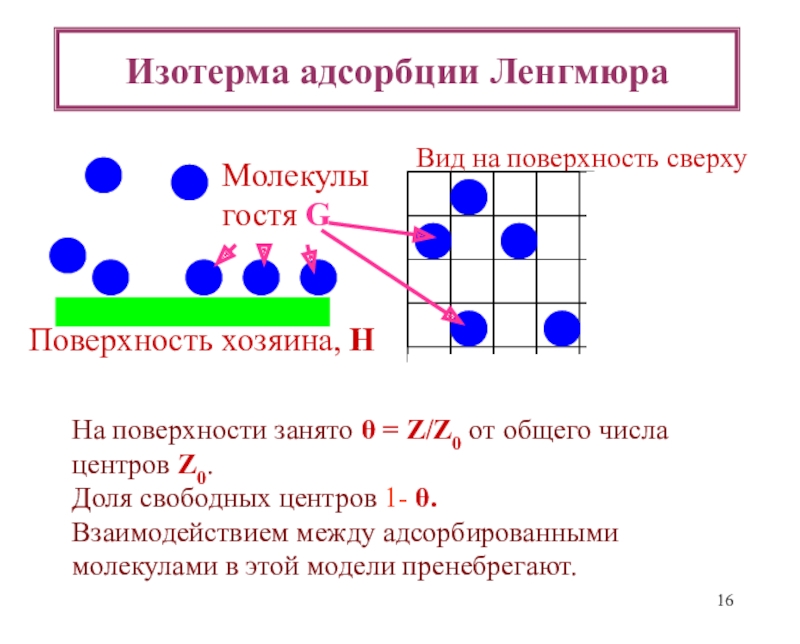
![Лекция 2 Динамический характер адсорбции При равновесии по схеме А2 + 2 [Z] 2[AZ] адсорбция При равновесии по схеме А2 + 2 [Z] 2[AZ] адсорбция А2 в виде 2А требует наличия](/img/thumbs/6e5d6750d1fc4903e4373a7a5672fd0e-800x.jpg)
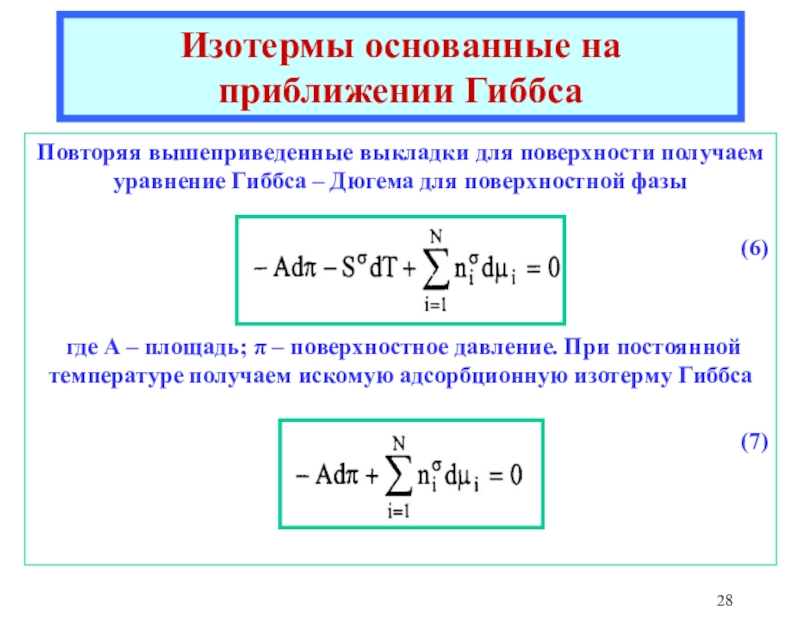

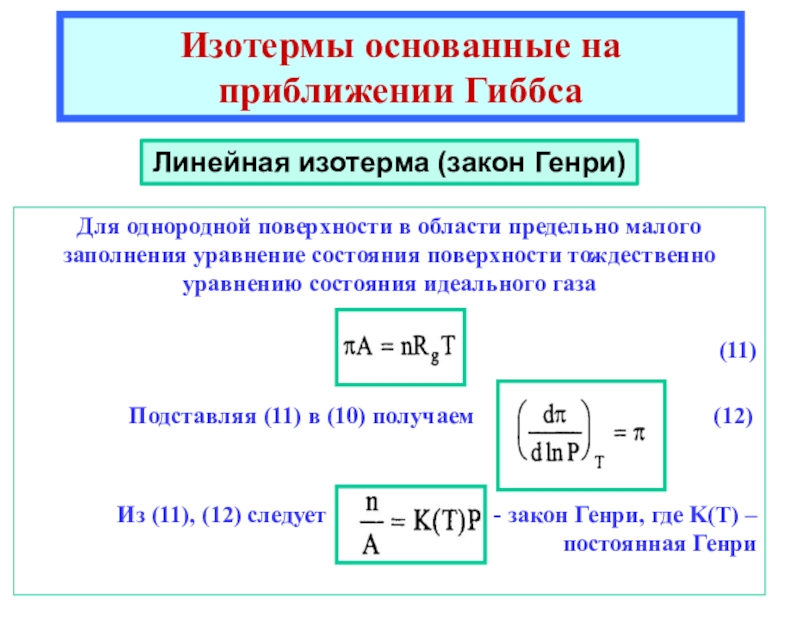




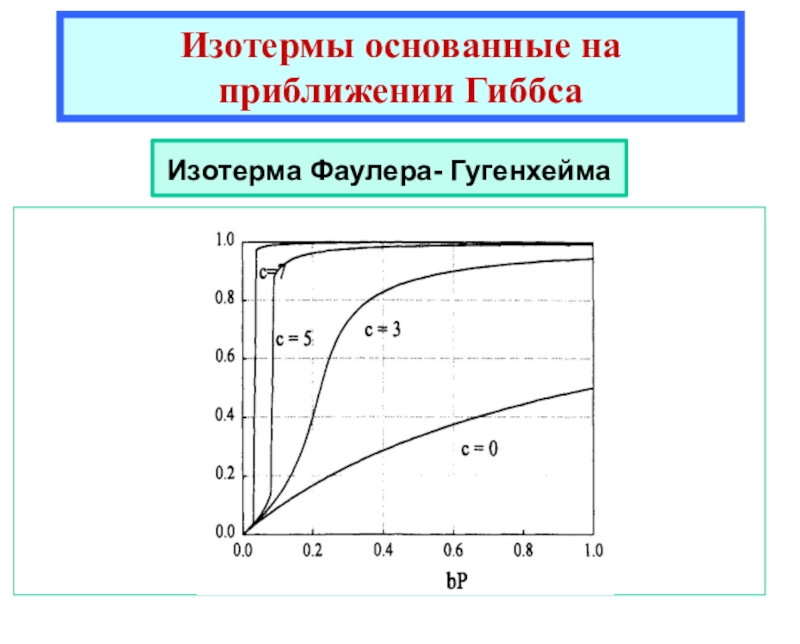
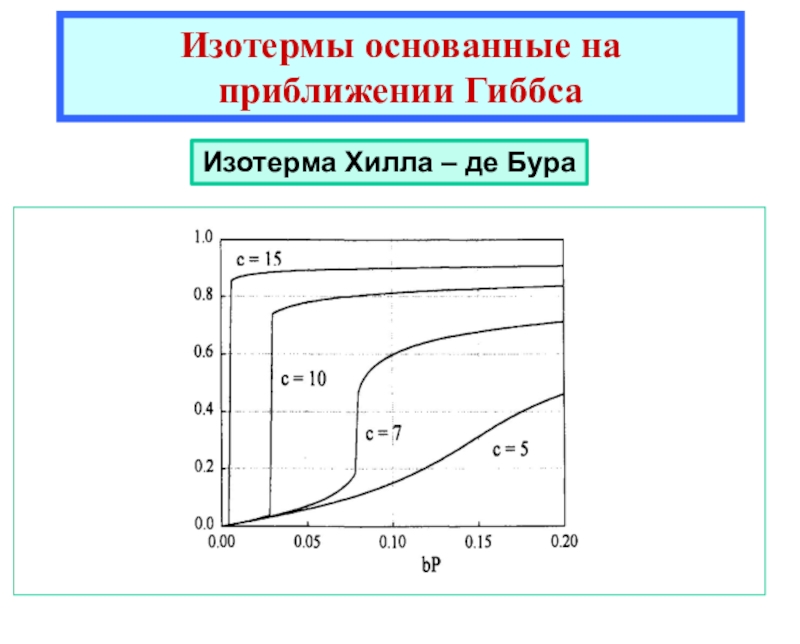


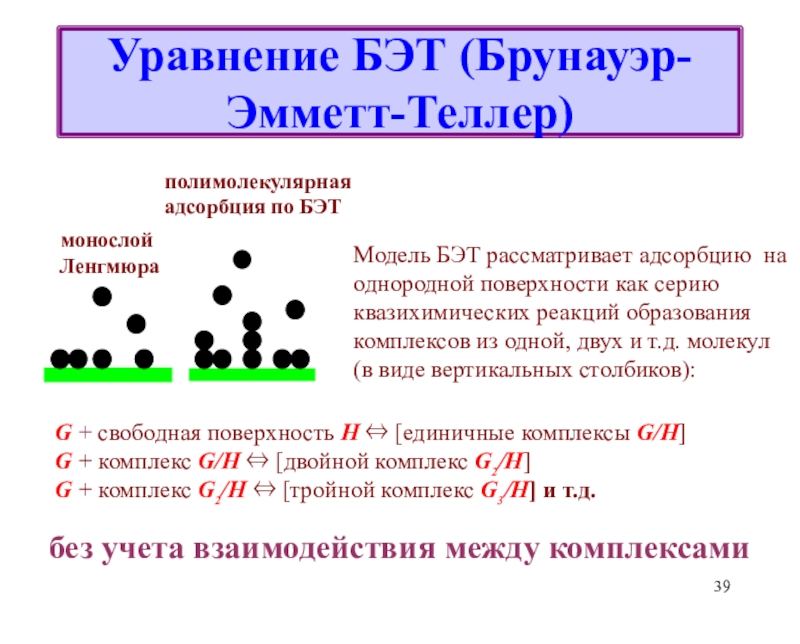
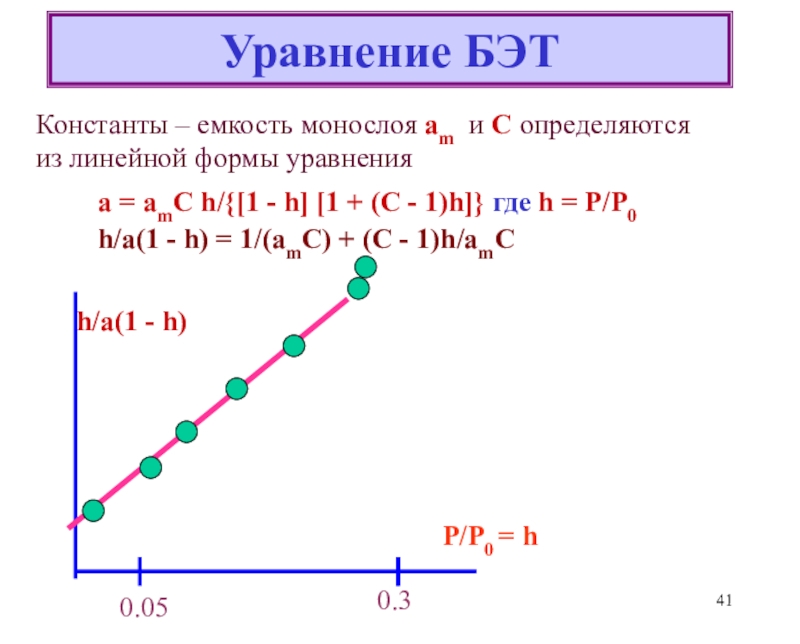
![Лекция 2 Динамический характер адсорбции а = аmC h/{[1 - h] [1 + (C - 1)h]}где а = аmC h/{[1 - h] [1 + (C - 1)h]}где h = P/P0Уравнение БЭТКонстанты уравнения БЭТ:am](/img/thumbs/49a392a94afbe6223ee29f15c51231a0-800x.jpg)