Лекция 2 Основы начертательной геометрии Предмет начертательная

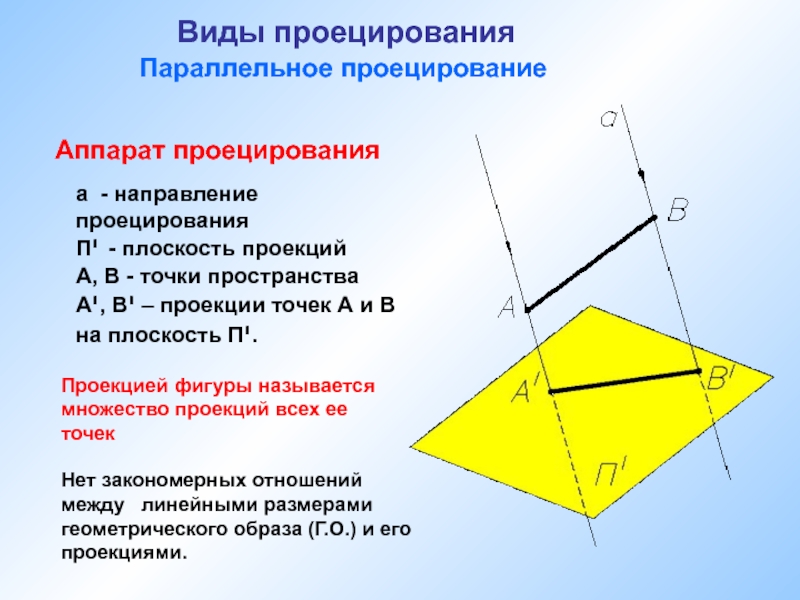
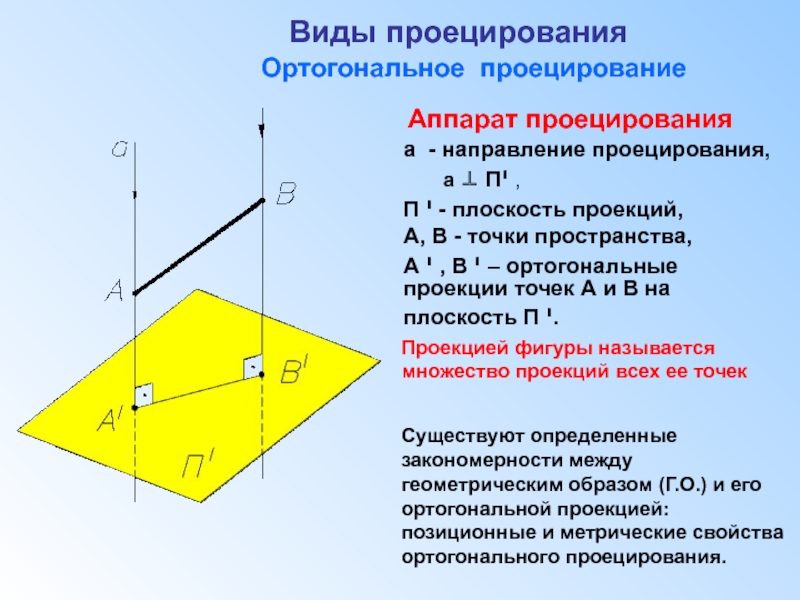
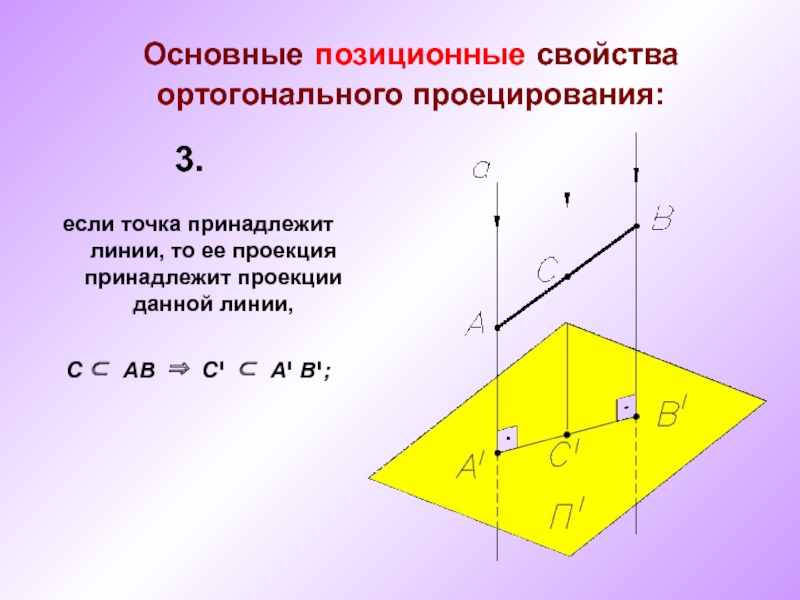
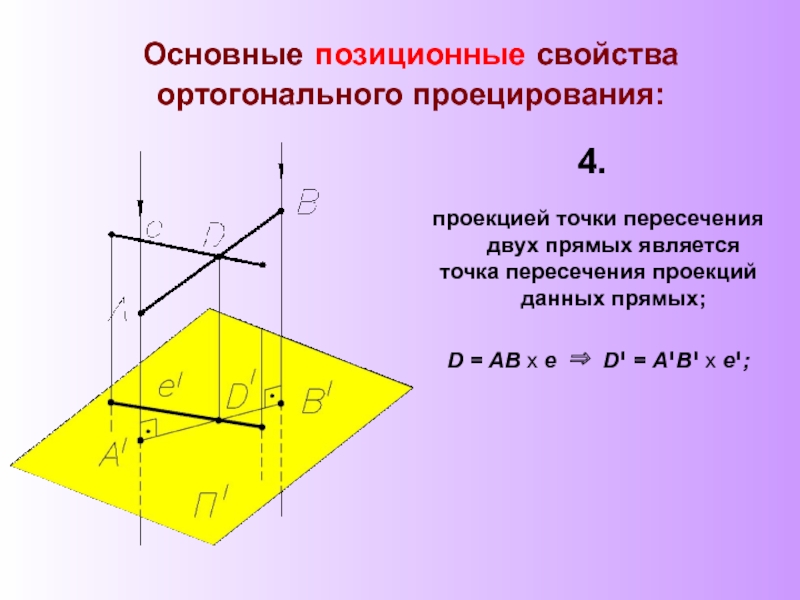
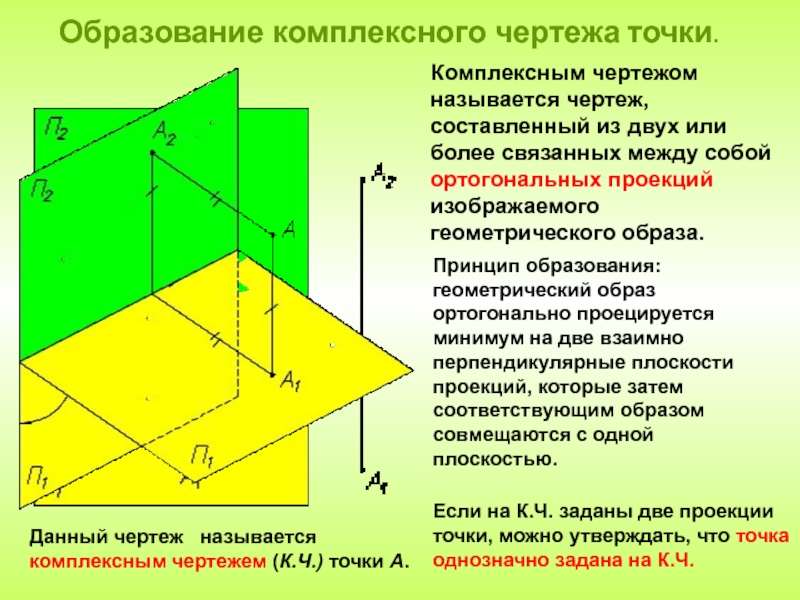
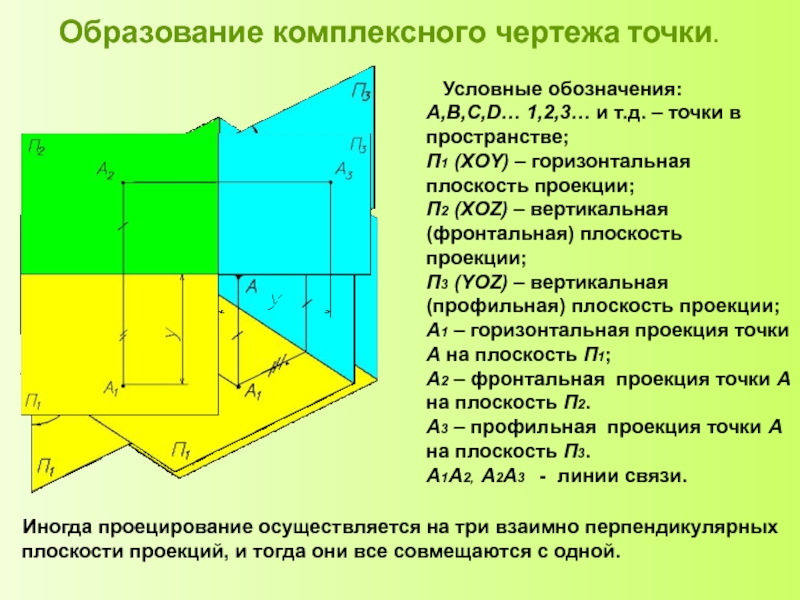
чертеж точки.
Виды проецирования. Свойства ортогонального проецирования.
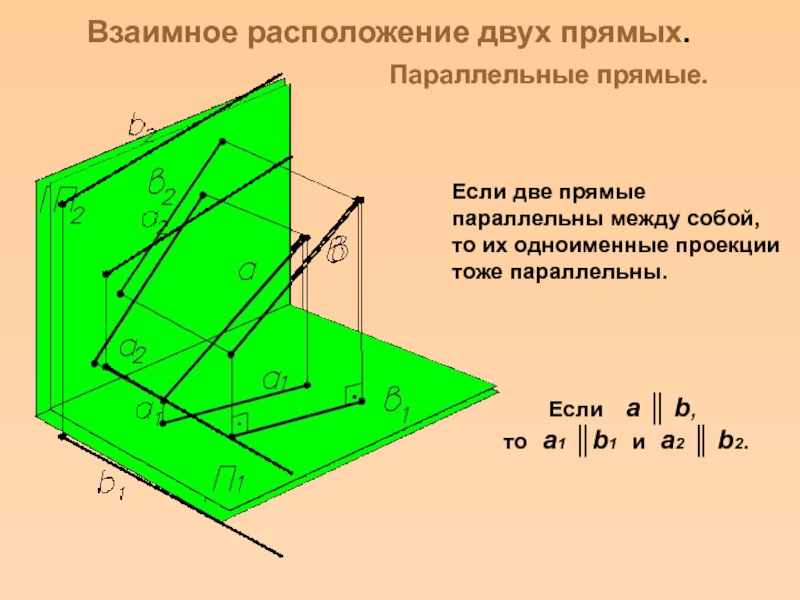
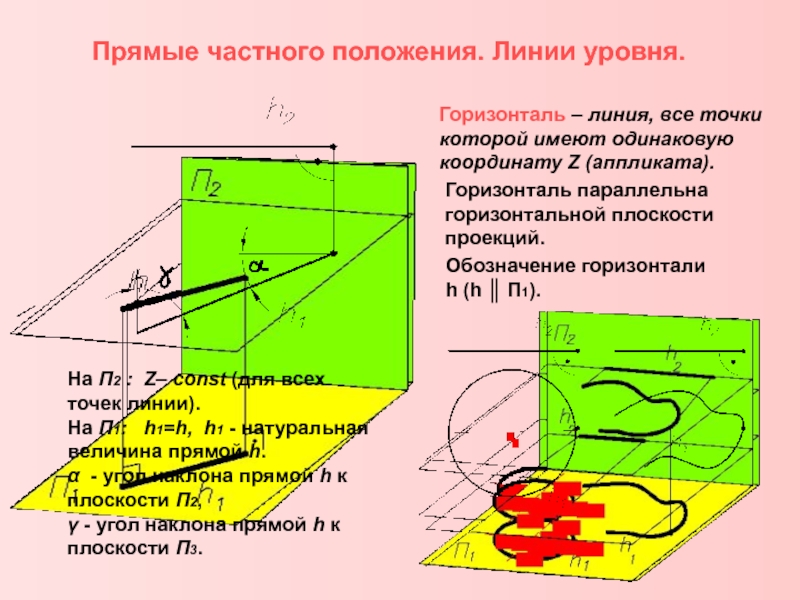
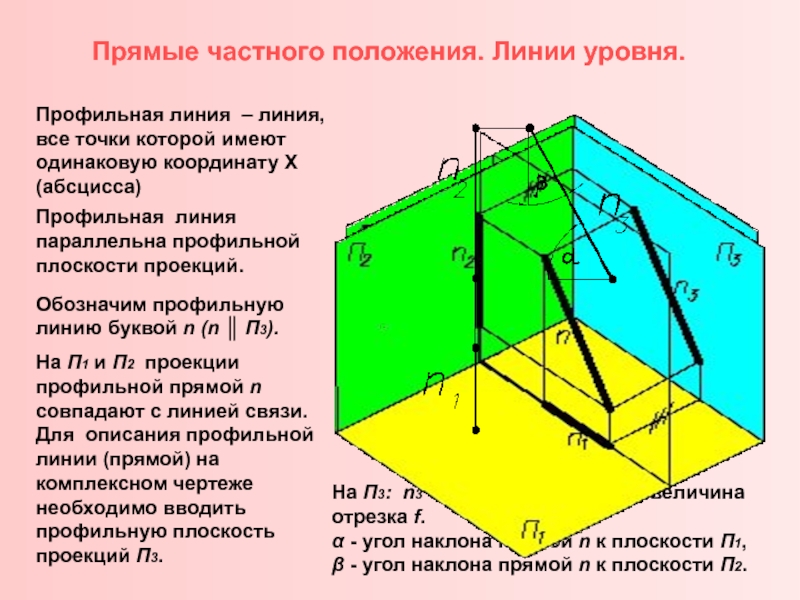
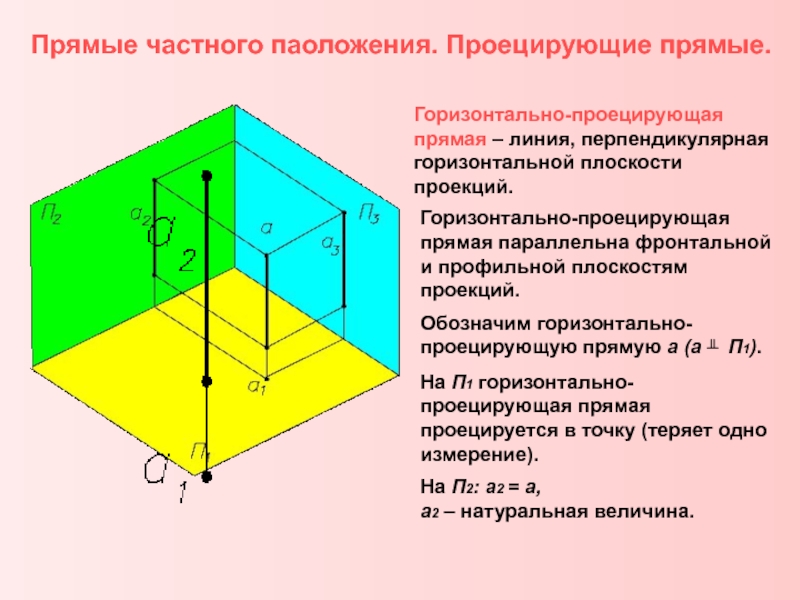
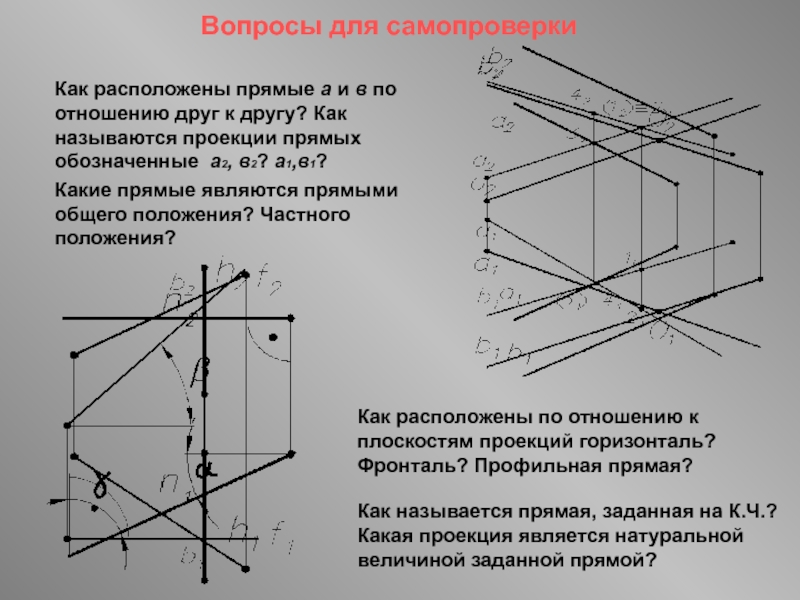
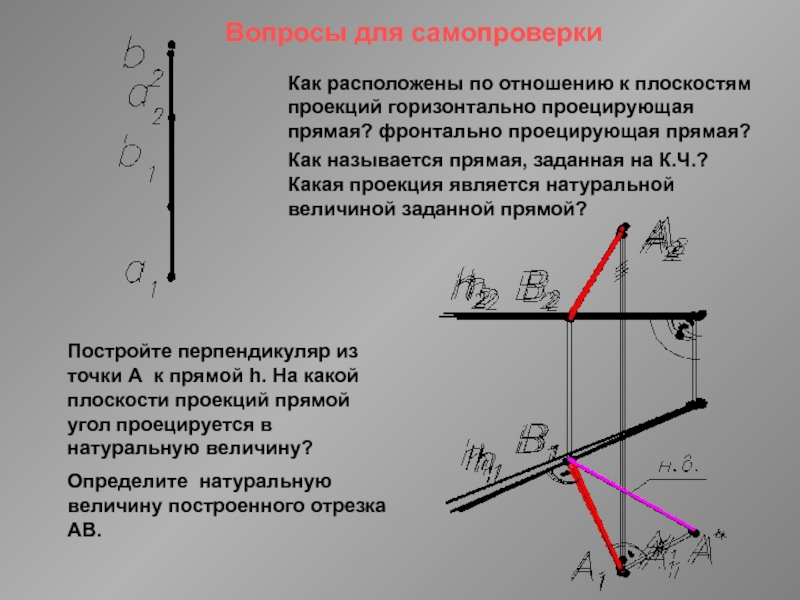
Комплексный чертеж линии. Взаимное расположение

Положение линий относительно плоскостей проекций.

«Очарование, сопровождающее науку, может победить свойственное людям отвращение к напряжению ума и заставить их находить удовольствие в упражнении своего разума…» (Гаспар Монж)

трехмерного пространства на двумерную плоскость методами проекций и сечений.

Основоположником начертательной

прямая -
построить изображение пространственного предмета на чертеже;

обратная –
реконструкция пространственного предмета по чертежу.

Построение любого изображения выполняется с помощью операции проецирования.

или картинная плоскость,
А, В - точки пространства,
SА, SВ

Аппарат проецирования

Проекцией фигуры называется множество проекций всех ее точек

Нет закономерных отношений между линейными размерами геометрического образа (Г.О.) и его проекциями.

В - точки пространства
Аי, Вי – проекции точек А

Аппарат проецирования

Проекцией фигуры называется множество проекций всех ее точек

Нет закономерных отношений между линейными размерами геометрического образа (Г.О.) и его проекциями.

- плоскость проекций,
А, В - точки пространства,
А י

Проекцией фигуры называется множество проекций всех ее точек

Аппарат проецирования

Существуют определенные закономерности между геометрическим образом (Г.О.) и его ортогональной проекцией: позиционные и метрические свойства ортогонального проецирования.

точка на плоскости проекций,
А  Аי;

1.
(обратная зависимость неоднозначна);

линия
Аי Вי,

АВ  Аי Вי;

АВАיВי– проецирующая плоскость L);
2.

проекция принадлежит проекции данной линии,

С  АВ  Сי 

3.

точка пересечения проекций данных прямых;

D = АВ х е 

4.

прямых являются
две параллельные прямые,

а II AB  аי

5.

равны соответствующим отношениям между их проекциями.

|АС| : |СВ|= |АיСי |

1.

на косинус угла наклона отрезка к плоскости проекций.

|АС| : |АВ|

2.

Примечания:
если α = 0о, то │АВ│=│АיВי│;
если α = 90о, то │АיВי│= 0.

Отрезок АВ (натуральная величина) является гипотенузой прямоугольного треугольника АВС, один катет которого является проекцией этого отрезка, а второй приращением координат точек А и В.

прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна,

3.

Если прямой угол проецируется ортогонально в виде прямого угла, то он имеет сторону, расположенную параллельно плоскости проекций.

Теорема о проецировании прямого угла:

Обратная теорема:

второй плоскости проекции или числовой отметки, указывающей расстояние от точки

Вышеприведенные чертежи называются однокартинными.

Рассмотренные методы проецирования позволяют однозначно решить прямую задачу – построить проекцию (чертеж) геометрического образа.

Обратная задача начертательной геометрии – по данному чертежу реконструировать геометрический образ – решается неоднозначно (может быть несколько или бесчисленное множество решений).

Из этого следует, что однокартинный чертеж не обладает свойством обратимости.

составленный из двух или более связанных между собой ортогональных проекций

Принцип образования: геометрический образ ортогонально проецируется минимум на две взаимно перпендикулярные плоскости проекций, которые затем соответствующим образом совмещаются с одной плоскостью.

Данный чертеж называется комплексным чертежем (К.Ч.) точки А.

Если на К.Ч. заданы две проекции точки, можно утверждать, что точка однозначно задана на К.Ч.

три взаимно перпендикулярных плоскости проекций, и тогда они все совмещаются

Условные обозначения:
A,В,С,D… 1,2,3… и т.д. – точки в пространстве;
П1 (XOY) – горизонтальная плоскость проекции;
П2 (XOZ) – вертикальная (фронтальная) плоскость проекции;
П3 (YOZ) – вертикальная (профильная) плоскость проекции;
А1 – горизонтальная проекция точки А на плоскость П1;
А2 – фронтальная проекция точки А на плоскость П2.
А3 – профильная проекция точки А на плоскость П3.
А1А2, А2А3 - линии связи.

перемещением точки.
Прямая однозначно задана на комплексном чертеже, если заданы

Линия – одномерный геометрический образ.

Обозначение линий – a, b, c, d … и т.д.

собой, то их одноименные проекции тоже параллельны.

Если a ║

если точки пересечения одноименных проекций прямых лежат на одной линии

Если a Х b = О,

то a1 Х b1 =О1
и a2 Х b2 = О2

скрещиваются между собой, если точки пересечения их одноименных проекций лежат

а ÷ b

Точки 1 и 2, 3 и 4 –
конкурирующие точки.

Конкурирующие точки –
Точки, лежащие на одной
Проецирующей прямой.

плоскостей проекций прямые разделяют на прямые общего положения и прямые

Прямая общего положения – прямая, которая имеет углы, отличные от 0° и 90° одновременно со всеми тремя плоскостями проекции (П1, П2 и П3).

Прямые, параллельные плоскостям проекций или перпендикулярные к ним, называются прямыми частного положения.

имеют одинаковую координату Z (аппликата).
Горизонталь параллельна горизонтальной плоскости проекций.
Обозначение горизонтали

На П2 : Z– const (для всех точек линии).
На П1: h1=h, h1 - натуральная величина прямой h.
α - угол наклона прямой h к плоскости П2,
γ - угол наклона прямой h к плоскости П3.

имеют одинаковую координату Y (ордината).
Фронталь параллельна фронтальной плоскости проекций.

Обозначение фронтали f (f ║ П2).

На П1 : Y – const (для всех точек прямой)
На П2: f2 = f, f2 - натуральная величина отрезка f.
β - угол наклона прямой f к плоскости П1,
γ - угол наклона прямой f к плоскости П3.

которой имеют одинаковую координату X (абсцисса)
Профильная линия параллельна профильной

Обозначим профильную линию буквой n (n ║ П3).

На П1 и П2 проекции профильной прямой n совпадают с линией связи. Для описания профильной линии (прямой) на комплексном чертеже необходимо вводить профильную плоскость проекций П3.

На П3: n3 = n, n3 - натуральная величина отрезка f.
α - угол наклона прямой n к плоскости П1,
β - угол наклона прямой n к плоскости П2.

плоскости проекций.
Горизонтально-проецирующая
прямая параллельна фронтальной
и профильной плоскостям проекций.
Обозначим горизонтально-проецирующую прямую

На П1 горизонтально-проецирующая прямая проецируется в точку (теряет одно измерение).

На П2: а2 = а,
а2 – натуральная величина.

плоскости проекций
Фронтально-проецирующая прямая параллельна горизонтальной и профильной плоскости проекций.
Обозначим

На П2 фронтально-проецирующая прямая проецируется в точку (теряет одно измерение).

На П1: b1 = b,
b1 – натуральная величина.

основных позиционных свойств ортогонального проецирования.
Может ли при ортогональном проецировании длина

Проецируется ли при ортогональном проецировании любой прямой угол в натуральную величину? Какое условие должно быть при этом выполнено?

Что такое однокартинный чертеж? Является ли однокартинный чертеж обратимым?

Что необходимо сделать, чтобы чертеж стал обратимым?

Какой чертеж называется комплексным?

Сколько проекций точки на К.Ч. должно быть задано, чтобы она была задана однозначно? А сколько проекций линии?

Какая точка расположена выше А или В?
А какая ближе?

друг к другу? Как называются проекции прямых обозначенные а2, в2?

Какие прямые являются прямыми общего положения? Частного положения?

Как расположены по отношению к плоскостям проекций горизонталь? Фронталь? Профильная прямая?

Как называется прямая, заданная на К.Ч.?
Какая проекция является натуральной величиной заданной прямой?

проецирующая прямая? фронтально проецирующая прямая?
Как называется прямая, заданная на К.Ч.?
Какая

Постройте перпендикуляр из точки А к прямой h. На какой плоскости проекций прямой угол проецируется в натуральную величину?

Определите натуральную величину построенного отрезка АВ.