Слайд 1Лекция 3. Электростатическое поле в диэлектрике
Слайд 2Вопросы:
Электрический диполь в электростатическом поле.
Поляризация диэлектриков. Поляризованность.
Электростатическое поле в диэлектрике.
Свободные и связанные заряды.
Теорема Гаусса для вектора поляризован-ности.
Связь поляризованности с
плотностью связанных зарядов.
Обобщение теоремы Гаусса для диэлект-риков. Вектор электрического смещения.
Поле на границе раздела диэлектриков.
Слайд 3Электрический диполь в электростатическом поле
Электрический диполь – это простейшая электрическая
система из двух одинаковых по модулю разноименных точечных зарядов +q
и –q, находящихся на некотором малом расстоянии l (плечо диполя).
Причем, когда говорят о поле диполя, то предполагают сам диполь – точечным, т.е. считают расстояние от диполя до интересующей точки поля r >> l. Прямую, проходящую через оба заряда, принято называть осью диполя.
Напоминание:
Слайд 4Электрический диполь в электростатическом поле
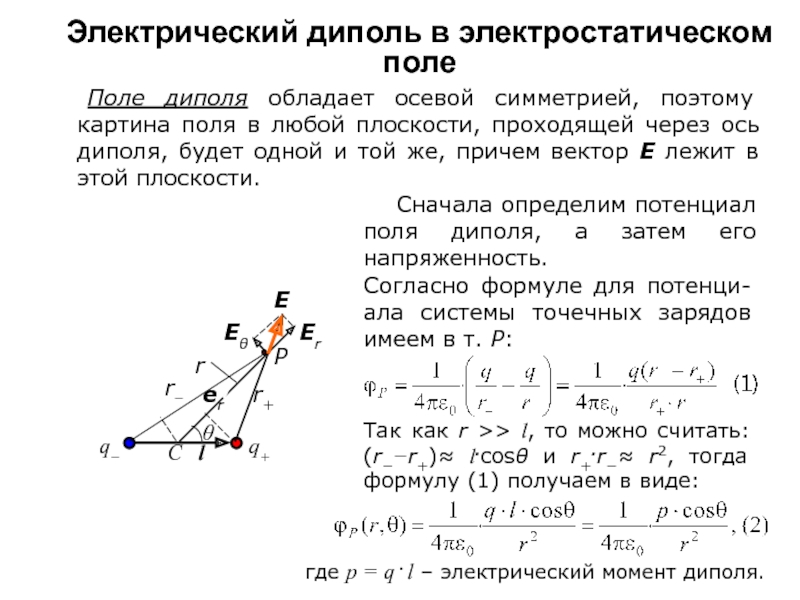
Поле диполя обладает осевой симметрией, поэтому
картина поля в любой плоскости, проходящей через ось диполя, будет
одной и той же, причем вектор Е лежит в этой плоскости.
Сначала определим потенциал поля диполя, а затем его напряженность.
Согласно формуле для потенци-ала системы точечных зарядов имеем в т. Р:
Так как r >> l, то можно считать: (r−−r+)≈ l.cosθ и r+.r−≈ r2, тогда формулу (1) получаем в виде:
где p = q . l – электрический момент диполя.
Слайд 5Электрический диполь в электростатическом поле
Для нахождения напряженности поля
диполя восполь-зуемся соотношением , разложив
результирующий вектор Е на два взаимно перпендикулярных направления – вдоль ортов er и eθ, т. е.
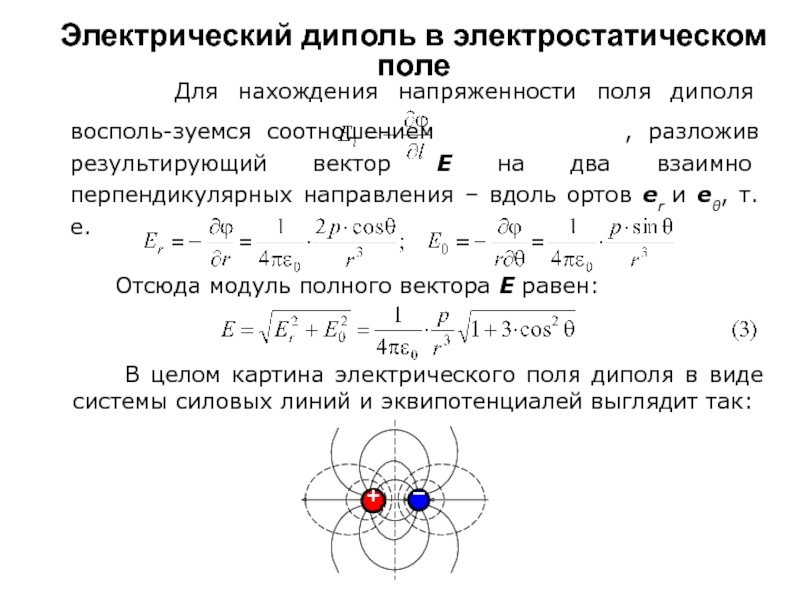
Отсюда модуль полного вектора Е равен:
В целом картина электрического поля диполя в виде системы силовых линий и эквипотенциалей выглядит так:
Слайд 6Электрический диполь в электростатическом поле
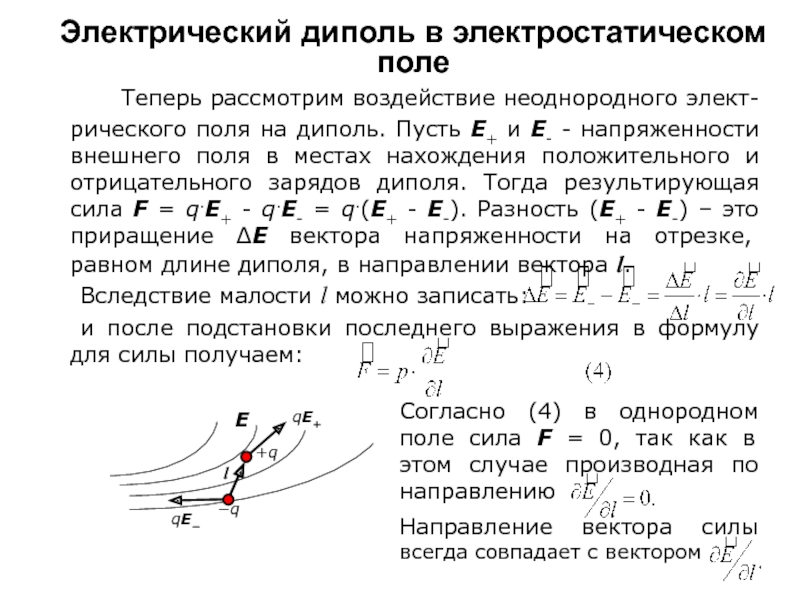
Теперь рассмотрим воздействие неоднородного
элект-рического поля на диполь. Пусть Е+ и Е- - напряженности
внешнего поля в местах нахождения положительного и отрицательного зарядов диполя. Тогда результирующая сила F = q.E+ - q.E- = q.(E+ - E-). Разность (Е+ - Е-) – это приращение ΔЕ вектора напряженности на отрезке, равном длине диполя, в направлении вектора l.
Вследствие малости l можно записать:
и после подстановки последнего выражения в формулу для силы получаем:
Согласно (4) в однородном поле сила F = 0, так как в этом случае производная по направлению
Направление вектора силы всегда совпадает с вектором
Е
Слайд 7Электрический диполь в электростатическом поле
Далее определим момент сил,
действующих на диполь. Рассмотрим поведение диполя во внешнем электрическом поле
в системе отсчета центра масс (центр диполя С). Согласно определению момент внешних сил F+ = q.E+ и F− = q.E− относительно С равен:
M = (r+ x F+) + (r− x F−) = (r+ x qE+) – (r− x qE−).
При достаточно малом расстоянии между зарядами диполя имеем: Е+ ≈ Е− и М = ((r+ - r−) x qE), а с учетом, что (r+ - r−) = l и ql = p, получаем
М = (р х Е) = р.Е.sinα (5)
Выводы: 1. Момент сил (5) стремится повернуть диполь так, чтобы его дипольный момент р установился по направлению внешнего поля Е – в этом случае (р↑↑Е) положение диполя является устойчивым. 2. Под действием результирующей силы (4) диполь перемещается в область большего поля Е, где больше концентрация силовых линий.
Слайд 8Поляризация диэлектриков. Поляризованность
Все тела состоят из
молекул и атомов. Последние представляют собой сложные системы из элементарных
электрических зарядов и в нормальных условиях в целом электрически нейтральны.
Определение: Тела, в которых часть микроскопических зарядов способна свободно перемещаться в пределах тела, называются проводниками. Они проводят электри-ческий ток посредством этих зарядов, которые принято называть свободными зарядами.
Определение: Тела, в которых все микроскопические заряды связаны друг с другом в пределах молекул (атомов), практически не проводят электрический ток и называются диэлектриками (или изоляторами).
_________
Идеальных изоляторов в природе не существует; все вещества хотя бы в ничтожной степени проводят электрический ток. Однако вещества, относящиеся к диэлектрикам, проводят ток в 1015-1020 раз хуже проводников. К хорошим проводникам относятся: металлы, растворы (расплавы) солей, кислот, щелочей. Изоляторами являются: керамика (фарфор), резина, пластмассы, стекло.
Слайд 9Поляризация диэлектриков. Поляризованность
При внесении даже нейтрального
диэлектрика во внешнее электрическое поле – происходят существенные изменения как
в самом поле, так и в диэлектрике.
Диэлектрики состоят либо из нейтральных молекул, либо из заряженных ионов, находящихся в узлах кристаллической решетки (так называемые ионные кристаллы, например, NaCl).
Сами молекулы могут быть: а) полярными, у которых центр «тяжести» отрицательного заряда сдвинут относительно центра «тяжести» положительного заряда и, следовательно, такие молекулы обладают собственным дипольным моментом р; б) неполярными, у которых центры «тяжести» отрицательного и положительного зарядов совпадают и, следовательно, такие молекулы не обладают дипольным моментом р = 0.
_________
Дипольный момент молекулы можно определить как , где qi – соответствующий заряд электронов и положительных ядер, - осредненный по времени радиус-вектор соответствующего заряда относительно центра молекулы.
Слайд 10Поляризация диэлектриков. Поляризованность
Под действием внешнего электрического
поля происходит поляризация диэлектрика. Это явление заключается в следующем (возможны
три варианта развития процесса):
1) если диэлектрик состоит из неполярных молекул (например, молекулярные газы O2, H2, N2), то в пределах каждой молекулы происходит смещение зарядов – положительных по полю, отрицательных против поля, и в итоге такие молекулы приобретают дипольный момент;
2) если диэлектрик состоит из полярных молекул (например, молекулы CO, NH, HCl), то их дипольные моменты ориентируются преимущественно по полю (в отсутствии внешнего поля их дипольные моменты из-за теплового движения были ориентированы хаотически, и суммарный момент всего диэлектрика был равен нулю);
3) в ионных кристаллах (типа NaCl) при включении внешнего электрического поля все положительные ионы смещаются по полю, а отрицательные – против поля.
Слайд 11Поляризация диэлектриков. Поляризованность
Механизм поляризации связан с
конкретным строением диэлектрика. Однако для дальнейших рассуждений важно только то,
что в процессе поляризации происходит смещение микроскопических зарядов внутри диэлектрика (положительных – по полю, отрицательных – против поля) и образование суммарного дипольного момента диэлектрика , отличного от нуля.
Определение: Для характеристики поляризации в некоторой точке вещества вводится понятие, называемое поляризованностью (или вектором Р), как суммарный дипольный момент единицы объема вещества:
где ΔV- физически бесконечно малый объем, содержащий рассматриваемую точку. Размерность в СИ вектора Р: [Кл/м2].
Можно также представить поляризованность вещества как Р=n
, где п – концентрация молекул (п =ΔN/ΔV),
= средний дипольный момент одной молекулы, ΔN – число диполей (молекул).
Слайд 12Поляризация диэлектриков. Поляризованность
Связь вектора поляризованности с вектором
напряженности электрического поля.
Для изотропных диэлектриков поляризованность Р зависит
линейно от напряженности Е поля в веществе, т.е.
Р = ϰ.ε0.Е (7)
где ϰ – диэлектрическая восприимчивость вещества, которая не зависит от Е и характеризует свойства самого диэлектрика.
Замечание: Существуют, однако, диэлектрики, для которых связь (7) не применима. Это некоторые ионные кристаллы и электреты (вещества, поляризованные даже в отсутствии внешнего поля), а также сегнетоэлектрики, для последних эта связь сугубо нелинейная и зависит от предыстории состояния диэлектрика, т.е. от предшествующих значений Е (такое явление называют гистерезисом).
Слайд 13Электростатическое поле в диэлектрике. Свободные и связанные заряды
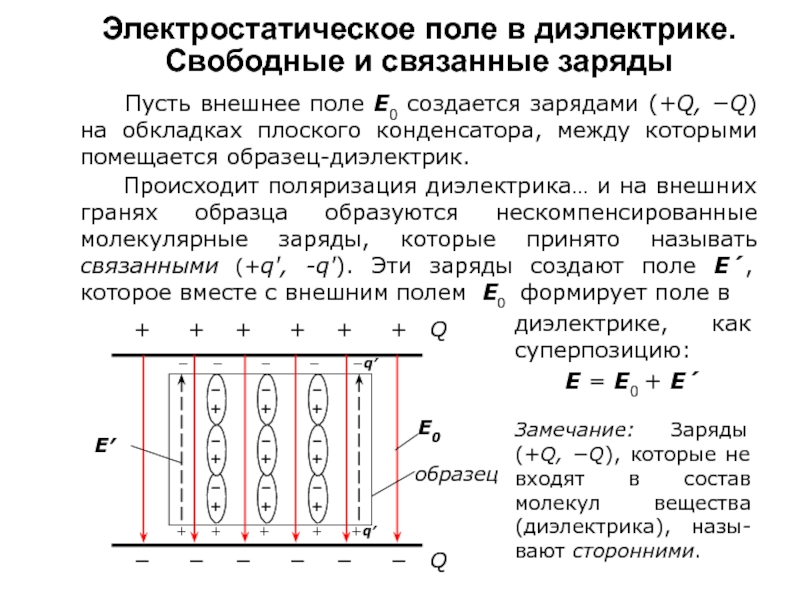
Пусть внешнее поле Е0 создается зарядами (+Q, −Q) на
обкладках плоского конденсатора, между которыми помещается образец-диэлектрик.
Происходит поляризация диэлектрика… и на внешних гранях образца образуются нескомпенсированные молекулярные заряды, которые принято называть связанными (+q', -q'). Эти заряды создают поле Е´, которое вместе с внешним полем Е0 формирует поле в
+ + + + +q′
− − − − −q′
− − − − − − Q
+ + + + + + Q
−
+
−
+
−
+
−
+
−
+
−
+
−
+
−
+
−
+
E0
E′
образец
диэлектрике, как суперпозицию:
Е = Е0 + Е´
Замечание: Заряды (+Q, −Q), которые не входят в состав молекул вещества (диэлектрика), назы-вают сторонними.
Слайд 14Электростатическое поле в диэлектрике. Свободные и связанные заряды
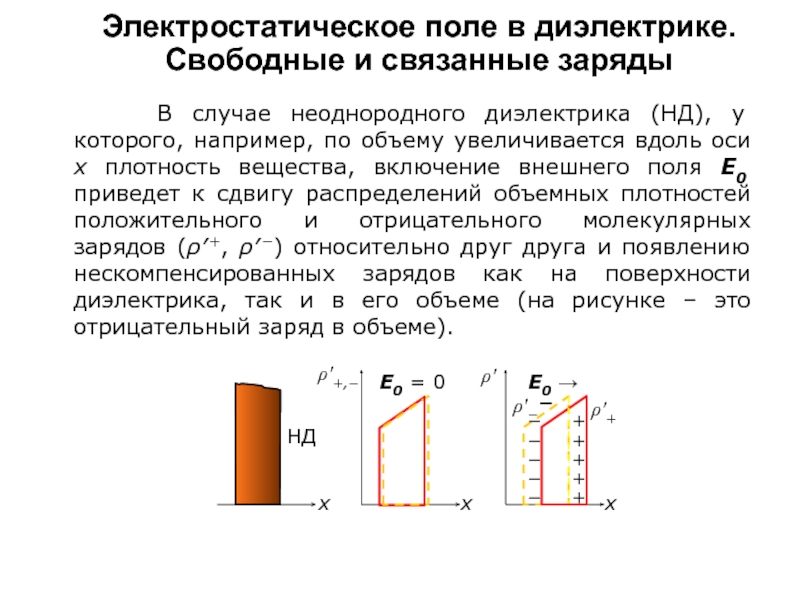
В случае неоднородного диэлектрика (НД), у которого, например, по
объему увеличивается вдоль оси х плотность вещества, включение внешнего поля Е0 приведет к сдвигу распределений объемных плотностей положительного и отрицательного молекулярных зарядов (ρ′+, ρ′−) относительно друг друга и появлению нескомпенсированных зарядов как на поверхности диэлектрика, так и в его объеме (на рисунке – это отрицательный заряд в объеме).
ρ′−
Е0 →
х
ρ′
ρ′+
+
+
+
+
+
−
−
−
−
−
−
Слайд 15Теорема Гаусса для вектора поляризованности
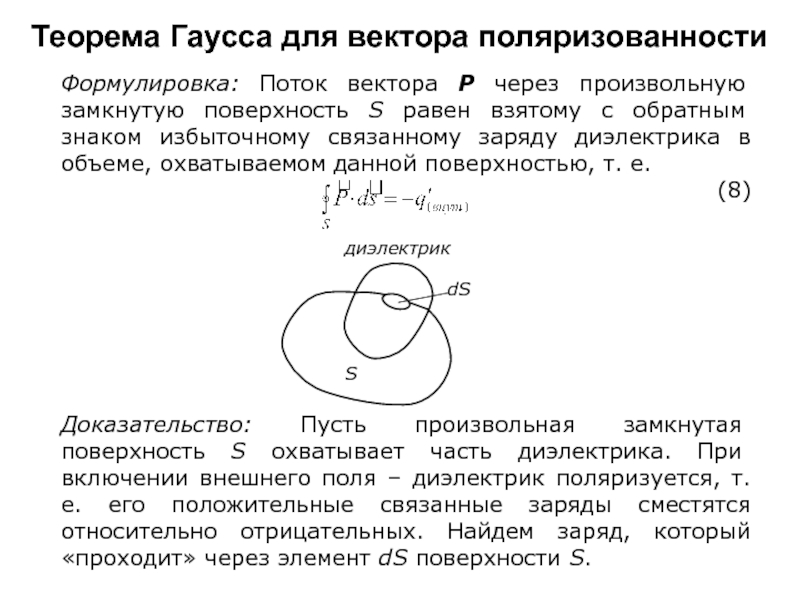
Формулировка: Поток вектора Р через произвольную
замкнутую поверхность S равен взятому с обратным знаком избыточному связанному
заряду диэлектрика в объеме, охватываемом данной поверхностью, т. е.
(8)
диэлектрик
S
dS
Доказательство: Пусть произвольная замкнутая поверхность S охватывает часть диэлектрика. При включении внешнего поля – диэлектрик поляризуется, т.е. его положительные связанные заряды сместятся относительно отрицательных. Найдем заряд, который «проходит» через элемент dS поверхности S.
Слайд 16Теорема Гаусса для вектора поляризованности
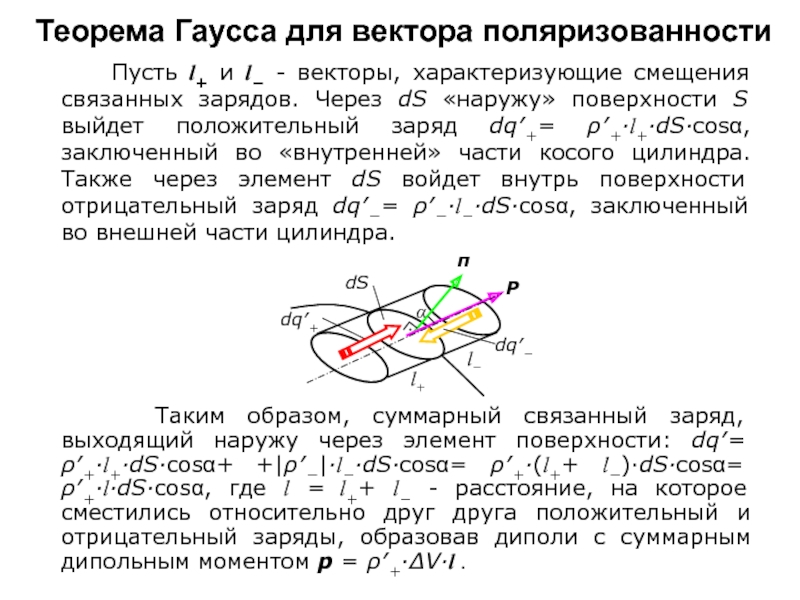
Пусть l+ и
l− - векторы, характеризующие смещения связанных зарядов. Через dS «наружу»
поверхности S выйдет положительный заряд dq′+= ρ′+∙l+∙dS∙cosα, заключенный во «внутренней» части косого цилиндра. Также через элемент dS войдет внутрь поверхности отрицательный заряд dq′−= ρ′−∙l−∙dS∙cosα, заключенный во внешней части цилиндра.
l−
l+
dq′+
α
Р
п
dq′−
dS
Таким образом, суммарный связанный заряд, выходящий наружу через элемент поверхности: dq′= ρ′+∙l+∙dS∙cosα+ +|ρ′−|∙l−∙dS∙cosα= ρ′+∙(l++ l−)∙dS∙cosα= ρ′+∙l∙dS∙cosα, где l = l++ l− - расстояние, на которое сместились относительно друг друга положительный и отрицательный заряды, образовав диполи с суммарным дипольным моментом р = ρ′+∙ΔV∙l .
Слайд 17Теорема Гаусса для вектора поляризованности
Модуль поляризованности представим
как Р = ρ′+∙ l, тогда искомый заряд в последнем
выражении можно записать: dq′ = P∙dS∙cosα = Pn∙dS = P∙dS
Затем проинтегрировав по всей замкнутой поверхности S, определим полный заряд, который вышел при поляризации диэлектрика из соответствующего объема:
Таким образом внутри поверхности S останется такой же избыточный связанный заряд с обратным знаком, т.е. q′ = −q′(внут) и в итоге мы доказали теорему.
Дифференциальная форма теоремы Гаусса для вектора Р
С помощью теоремы Остроградского – Гаусса и объемной плотности заряда ρ′ формуле (8) можно придать дифференциальную (локальную) форму:
Т.е. дивергенция поляризованности показывает наличие объемных избыточных связанных зарядов, как элементарных «источников» поля Р.
Слайд 18Связь поляризованности с плотностью связанных зарядов
Рассмотрим поведение
вектора Р на границе раздела двух однородных диэлектриков, для которых
в ходе поляризации появляются только поверхностные связан-ные заряды. Воспользуемся теоремой Гаусса в форме (8), где в качестве гауссовой поверхности возьмем малый прямой цилиндр с торцами ΔS по разные стороны границы и осью, ортогональной ей.
Пренебрегая потоком Р через боковую поверхность цилиндра, запишем уравнение для теоремы Гаусса:
Р2п∙ΔS + P1n′ ΔS = - σ′∙ΔS,
Р2п
Р1п
п′
п
Р1
1
2
Р2
ΔS
где q′= σ′∙ΔS, P2n и Р1п′ - проекции вектора Р в диэлектрике 2 на нормаль п и в диэлектрике 1 на нормаль п′. С учетом Р1п′ = - Р1п получаем уравнение для потока вектора Р в виде (P2n - Р1п)∙ΔS = - σ′∙ΔS или после сокращения на ΔS:
P2n - Р1п = - σ′ (10)
Слайд 19Связь поляризованности с плотностью связанных зарядов
Таким образом,
на границе раздела диэлектриков нормальная составляющая вектора Р терпит разрыв,
величина которого зависит от σ′.
В частности, если среда 2 – вакуум и P2n = 0, то условие (10) принимает вид:
σ′ = Рп (11)
где Рп – проекция вектора Р на внешнюю нормаль к поверхности данного диэлектрика. Причем, знак проекции Рп определяет и знак σ′ в данном месте.
С учетом связи Р = ϰ.ε0.Е можно также записать для поверхностной плотности связанных зарядов σ′ = ϰ.ε0.Еп, где Еп – проекция вектора напряженности электрического поля в диэлектрике на внешнюю нормаль.
Слайд 20Обобщение теоремы Гаусса для диэлектриков. Вектор электрического смещения
Формулировка: Поток
вектора напряженности электри-ческого поля в диэлектрике через замкнутую поверхность S
равен алгебраической сумме сторонних и связанных зарядов, охватываемых рассматриваемой поверхностью, деленной на ε0, т. е.
Появление связанных зарядов q′ усложняет дальнейший расчет Е по (12). Эту трудность можно обойти, если выразить заряд q′ через поток вектора Р по (8), тогда уравнение (12) после умножения на ε0 примет вид:
Величину, стоящую под интегралом в скобках, обозначают как D = ε0∙E + P и называют вектором электрического смещения.
Слайд 21Обобщение теоремы Гаусса для диэлектриков. Вектор электрического смещения
Введение вектора электрического смещения значи-тельно упрощает анализ и расчет электрического
поля в диэлектрике. Это связано с тем, что поток вектора D через замкнутую поверхность S равен алгебраической сумме сторонних зарядов, охватываемых данной поверхностью, т. е.
Замечание: Единицей измерения вектора D в СИ является 1 [Кл/м2].
Дифференциальная форма теоремы Гаусса для D:
дивергенция электрического смещения равна объемной плотности сторонних зарядов в данной точке, т. е.
Слайд 22Обобщение теоремы Гаусса для диэлектриков. Вектор электрического смещения
Связь
между векторами D и E
В случае изотропных
диэлектриков имеем Р = ϰ.ε0.Е, подставив это соотношение в определение вектора электрического смещения, получаем D = ε0∙(1 + ϰ)∙E или, вводя понятие – диэлектрическая проницаемость вещества ε = 1 + ϰ (электрическая характеристика диэлектрика, зависит от его природы), получаем:
D = ε∙ε0∙E (15)
Замечание: Для вакуума ε = 1; для газов ε ≥ 1; для воды ε ≈ 80; для керамики ε ~ 103.
Поле вектора D можно изобразить с помощью линий вектора D (подобно полю Е). Отличие: линии Е могут начинаться и заканчиваться как на сторонних, так и на связанных зарядах, а «источниками» и «стоками» поля D являются только сторонние заряды (через области, где находятся связанные заряды, линии D проходят не прерываясь).
Слайд 23Обобщение теоремы Гаусса для диэлектриков. Вектор электрического смещения
Расчет
электрического поля в присутствии диэлектрика
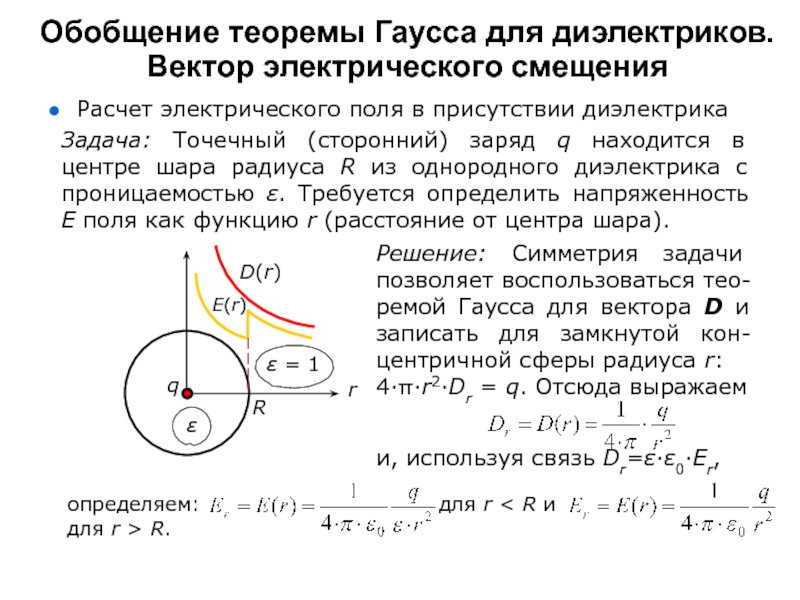
Задача: Точечный (сторонний) заряд q находится
в центре шара радиуса R из однородного диэлектрика с проницаемостью ε. Требуется определить напряженность Е поля как функцию r (расстояние от центра шара).
R
r
E(r)
D(r)
ε = 1
ε
q
Решение: Симметрия задачи позволяет воспользоваться тео-ремой Гаусса для вектора D и записать для замкнутой кон-центричной сферы радиуса r:
4∙π∙r2∙Dr = q. Отсюда выражаем
и, используя связь Dr=ε∙ε0∙Er,
определяем: для r < R и
для r > R.
Слайд 24Поле на границе раздела диэлектриков
Рассмотрим поведение векторов
E и D на границе раздела двух однородных изотропных диэлектриков
(с проницаемостями ε1 и ε2). Пусть для общности на границе этих диэлектриков находится поверхностный сторонний заряд с плотностью σ.
Искомые условия получим с помощью двух теорем:
1) теоремы о циркуляции вектора Е, т. е.
2) теоремы Гаусса для вектора D, т. е.
Для поля вектора Е
Пусть поле вблизи границы раздела в диэлектрике 1 есть Е1, а в диэлектрике 2 – Е2. Возьмем малый вытянутый прямоугольный контур Г, ориентировав его как на рисунке.
τ
τ
1
2
l
τ′
Г
Е1
Е2
Тогда согласно теореме о циркуляции Е имеем E2τ∙l + E1τ′∙l = 0, где проекции Е взяты на направление обхода контура. Так как E1τ′ = - E1τ , то после подстановки получаем:
E1τ = E2τ (16)
Слайд 25Поле на границе раздела диэлектриков
Для поля вектора D
Возьмем очень малой высоты цилиндр, расположив его на границе раздела
двух диэлектриков. Сечение цилиндра ΔЅ должно быть таким малым, чтобы в пределах каждого его торца вектор D был одинаков.
Тогда согласно теореме Гаусса имеем D2n∙ΔЅ + D1n′∙ΔЅ = σ∙ΔЅ, а так как D1n′= -D1n то получаем условие для изменения D:
D2n - D1n = σ (17)
т. е. нормальная составляющая вектора D, вообще говоря, претерпевает «скачок» величиной в σ; если же сторонние заряды на границе раздела – отсутствуют (σ = 0), то имеем постоянство D1n = D2n.
п
ε1
ε2
п′
ΔЅ
D2
D1
Выводы: Если на границе раздела двух однородных диэлектриков – сторонних зарядов нет, то при переходе этой границы составляющие Еτ и Dn изменяются непрерывно (без скачка), а составляющие Еп и Dτ претерпевают скачок.
Слайд 26Поле на границе раздела диэлектриков
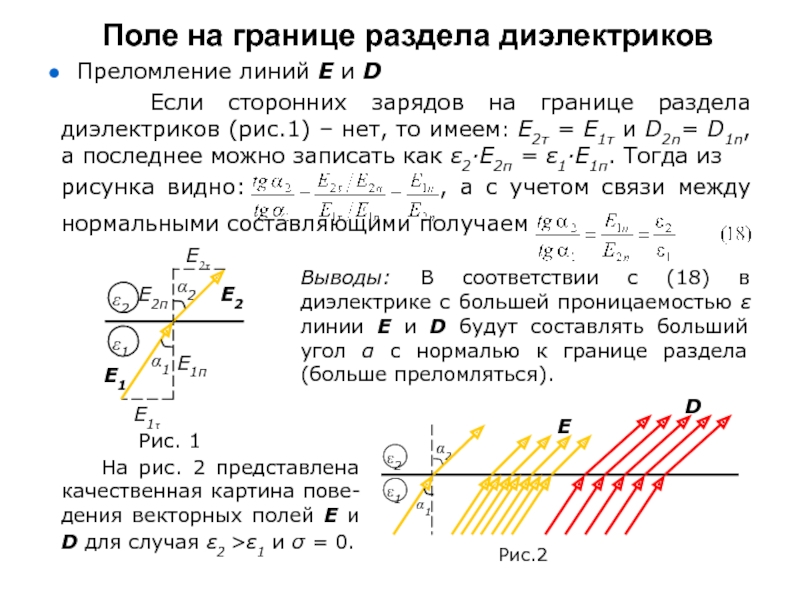
Преломление линий Е и D
Если сторонних зарядов на границе раздела диэлектриков (рис.1)
– нет, то имеем: Е2τ = Е1τ и D2n= D1n, а последнее можно записать как ε2∙Е2п = ε1∙Е1п. Тогда из
рисунка видно: , а с учетом связи между нормальными составляющими получаем
На рис. 2 представлена качественная картина пове-дения векторных полей Е и D для случая ε2 >ε1 и σ = 0.
Выводы: В соответствии с (18) в диэлектрике с большей проницаемостью ε линии Е и D будут составлять больший угол α с нормалью к границе раздела (больше преломляться).