Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 4
Содержание
- 1. Лекция 4
- 2. Пример 1В колоде имеется десять карточек. На
- 3. Решение:Прежде всего замечаем, что условия всех десяти
- 4. Развитие условия задачи из примера 1Составим теперь
- 5. В теоретико-множественных терминах пространство можно записать как
- 6. Последовательность независимых испытаний БернуллиПоследовательностью независимых испытаний называется
- 7. Схема БернуллиВ серии из независимых
- 8. Биноминальное распределениеСовокупность вероятностей ,
- 9. Всегда ли применима формула Бернулли?Формулы биномиального распределения
- 10. Теорема ПуассонаПусть при каждом испытании такой серии
- 11. Распределение ПуассонаРаспределение вероятностей, определяемое формулами
- 12. Пример 2В лотерее разыгрывается в среднем 1
- 13. Локальная теорема Муавра – ПуассонаРассмотрим другую предельную
- 14. Пример 3Оператор обслуживает 40 однотипных приборов. Вероятность
- 15. Интегральная предельная теорема Муавра – ЛапласаПри большом
- 16. Применение теоремы Муавра-ЛапласаЭта теорема является следствием центральной
- 17. Случайные величиныБудем рассматривать дискретное вероятностное пространство
- 18. Новое вероятностное пространствоОбозначим через множество тех
- 19. Таким образом, со случайной величиной
- 20. Случайная величина и функция распределенияВ общем случае
- 21. Основные свойства функции распределенияДля
- 22. Дискретная случайная величинаСлучайная величина называется
- 23. Пояснения по функции распределенияЭто следует из определения
- 24. Примеры:Пример1: Пусть - число успехов
- 25. Пример определения функции распределения д.с.в.Пример 3: Игроку
- 26. Функция распределения и её графикДля последней задачи, получаем следующую функцию распределения и её график:
- 27. Непрерывная случайная величинаСлучайная величина называется
- 28. свойства плотности вероятности Исходя из свойства 1
- 29. Пример непрерывной случайной величинынормальная случайная величина с плотностью вероятности
- 30. Двумерная функция распределениядвумерная функция распределения
- 31. Свойства двумерной функции распределенияФункция распределения удовлетворяет неравенству:
- 32. Дискретный и непрерывный случайный векторСлучайный вектор называется
- 33. Скачать презентанцию
Пример 1В колоде имеется десять карточек. На каждой карточке написаны различные числа от 1 до 10. Карточки тщательно перемешаны. Наудачу вынимается одна из них, записывается помещенное на ней число, и карточка
Слайды и текст этой презентации
Слайд 3Решение:
Прежде всего замечаем, что условия всех десяти испытаний: вынимание карточек
из колоды – одинаковы. Поэтому поставим в соответствие каждому из
них одинаковые вероятностные пространства , где пространство элементарных исходов включает следующие элементарные события - число чётное, - число нечётное, кратное трём, - остальные числа. Так как среди десяти чисел 1; 2;...; 10 - пять чётных (2; 4; 6; 8; 10), два нечётных, кратных трём (3 и 9), то соответствующие вероятности элементарных событий равны:Слайд 4Развитие условия задачи из примера 1
Составим теперь пространство элементарных событий
по результатам двух испытаний.
Тщательное перемешивание карточек после каждого
возвращения очередной их них в колоду и вынимание следующей карточки наудачу означает независимость результатов каждого испытания. Поэтому вероятности элементарных исходов из находим как произведение соответствующих вероятностей элементарных исходов пространства :Слайд 5В теоретико-множественных терминах пространство можно записать как произведение
(т.е. множество всех
упорядоченных пар ,где ). Продолжая аналогичные рассуждения, можно построить пространство элементарных исходов для последователь-ности всех десяти испытаний и вычислить вероятности элементарных исходов такого пространства. Полученные результаты позволят решить поставленную задачу. Не останавливаясь на подробностях метода вычисления вероятности, приведём лишь окончательный результат:, где событие - среди
десяти записанных цифр ровно четыре чётных и две нечётных, кратных трём
Слайд 6Последовательность независимых испытаний Бернулли
Последовательностью независимых испытаний называется дискретное вероятностное пространство
элементарными исходами в котором являются последовательности
и вероятность определена для
каждого элементарного события формулой:Последовательность независимых испытаний называются схемой Бернулли, если , т.е. если опыт S имеет лишь два исхода. Обычно в схеме Бернулли исход называют успехом и соответствующую вероятность обозначают , а - называют неудачей и .
Слайд 7Схема Бернулли
В серии из независимых испытаний в схеме
Бернулли вероятностное пространство состоит из элементарных событий, причем , где
- число успехов в последовательности исходов.Найдем вероятность того, что в серии из испытаний успех наступит раз. Так как при этом не имеет значения, когда именно в этих испытаниях будут наблюдаться успехов, то событие , состоящее в наступлении успехов, является объединением всех различных событий , в которых встречается раз. Всего таких элементарных событий в будет , а поскольку они несовместны, то искомая вероятность дается равенством (см. ниже)
Слайд 8Биноминальное распределение
Совокупность вероятностей ,
, называется биномиальным распределением
Пример 1:
Пусть вероятность попадания в цель при одном выстреле равна 0,6. Найти вероятность попаданий в цель при выстрелах. Из последней формулы находим следующие вероятности: ,
, ,
, ,
, ,
Слайд 9Всегда ли применима формула Бернулли?
Формулы биномиального распределения вероятностей приводят при
больших к очень громоздким вычислениям. Поэтому важно иметь
приближенные, но простые формулы. Найдем предельную формулу для биномиального распределения, когда число испытаний стремится к бесконечности, а вероятность успеха стремится к нулю.Пусть произвели некоторую серию независимых испытаний, состоящую из конечного числа испытаний, затем новую серию, затем еще одну и т.д. Получим последовательность серий испытаний.
Слайд 10Теорема Пуассона
Пусть при каждом испытании такой серии имеем два исхода
и вероятность успеха при отдельном испытании постоянна в пределах каждой
серии, но может меняться от серии к серии. В этих условиях справедлива следующаяТеорема Пуассона. Пусть дана последовательность серий независимых испытаний , состоящих соответственно из испытаний, и пусть вероятность события А при каждом испытании n-ой серии равна , где - постоянная, не зависящая от . Тогда вероятность того, что число наступлений события А в -й серии будет равно , при и фиксированном стремится к
Слайд 11Распределение Пуассона
Распределение вероятностей, определяемое формулами
,
, (2)называется распределением Пуассона. Эта формула получена как предельная для последовательности серий независимых испытаний, в которой число испытаний стремится к бесконечности, а вероятность наступления события А стремится к нулю так, что
Оценка погрешности, допускаемой при замене биномиального закона на закон Пуассона, приводит к следующему результату где .
На практике использование формулы может быть оправдано при и . Это значит, что распределение Пуассона описывает вероятности в задачах с «редкими успехами».
Слайд 12Пример 2
В лотерее разыгрывается в среднем 1 выигрыш на 1000
номеров. Какова вероятность, имея 100 билетов, получить хотя бы 2
выигрыша? Здесь n=100, p=0,001, тогда .0,0047
Слайд 13Локальная теорема Муавра – Пуассона
Рассмотрим другую предельную форму биномиального распределения,
считая, что вероятность успеха не мала и не близка к
единице.Локальная теорема Муавра – Пуассона. Если вероятность события А в n независимых испытаниях равна , то вероятность того, что в этих испытаниях событие А наступит раз, удовлетворяет соотношению
где
Слайд 14Пример 3
Оператор обслуживает 40 однотипных приборов. Вероятность того, что прибор
потребует внимания оператора в течение времени Т, равна 0,2. Найти
вероятность того, что за это время пять приборов потребуют внимания оператора.Используя последнюю формулу в приближенном виде
получаем
Расчет по точной формуле Бернулли дает т.е. относительная погрешность составляет ~9 %.
Слайд 15Интегральная предельная теорема Муавра – Лапласа
При большом числе испытаний
и не слишком малых вероятностях редко требуется знать вероятность наступления
события ровно раз. Чаще возникает задача оценки вероятности того, что число событий лежит в некоторых границах. Для решения этой задачи используется следующая теорема.Интегральная предельная теорема Муавра – Лапласа. Пусть - число наступлений события А в серии из независимых испытаний, - вероятность наступления события А при каждом испытании, , и - любые фиксированные числа, , Тогда
Слайд 16Применение теоремы Муавра-Лапласа
Эта теорема является следствием центральной предельной теоремы, которая
будет рассмотрена ниже. Практическое применение интегральной теоремы Муавра-Лапласа основано на
приближённом равенствекоторое обеспечивает хорошую точность при Функция
называется функцией Лапласа или интегралом ошибок. Её основные свойства:
Слайд 17Случайные величины
Будем рассматривать дискретное вероятностное пространство
и в качестве примера – схему независимых
испытаний Бернулли. Здесь пространство элементарных исходов состоит из элементарных событий - последовательностей вида:В схеме испытаний Бернулли нас интересовали события , где события составляют те последовательности, в которых успех встречается раз. Вероятность . Рассмотрим функцию , определённую на данном равенствами , , . Такая функция описывает число успехов в серии из n независимых испытаний Бернулли в том смысле, что число успехов в каждой последовательности испытаний равно по определению .
Слайд 18Новое вероятностное пространство
Обозначим через множество тех
, для которых . Следовательно,
по определению и или , . Это равенство называют распределением вероятности случайной величины . Оно задаёт вероятность на алгебре всех подмножеств множества значений случайной величины .Последнее в данном случае состоит из n+1 точек: Алгебра событий состоит из всех подмножеств .
Слайд 19Таким образом, со случайной величиной связано новое
вероятностное пространство ,
в котором пространством элементарных исходов является множество значений случайной величины, - алгебра всех подмножеств , а вероятность связана с вероятностью на исходном вероятностном пространстве формулой . Случайная величина задаёт отображение вероятностного пространства на вероятностное пространство . При этом каждой точке отвечает её прообраз в : множество .Слайд 20Случайная величина и функция распределения
В общем случае случайная величина определяется
следующим образом. Пусть - вероятностное пространство. Случайной величиной
называется однозначная действительная функция , определенная на , для которой множество элементарных событий вида является событием для каждого действительного числа х. Т.е функция является измеримой для любого значения В определении требуется, чтобы для каждого множество являлось событием, и это условие гарантирует, что для каждого x определена вероятность события . Функция ,называется функцией распределения случайной величины .
Слайд 21Основные свойства функции распределения
Для
Имеем . Из несовместности событий
в правой части равенстваследует . Отсюда и из определения функции распределения следует утверждение.
2. Функция - неубывающая.
Это следствие формулы (5) и свойства неотрицательности вероятности.
3.
Это следует из определения функции распределения.
4. Доказательства свойств (4,5) можно найти, например, в [4].
функция непрерывна слева.
6. Предел справа .
Слайд 22Дискретная случайная величина
Случайная величина называется дискретной, если множество
её значений конечно или счётно
Для полной характеристики дискретной случайной величины,
принимающей значения достаточно задать вероятности , . На практике соответствие между и задаётся в виде таблицы (закона) распределения:При этом , а
обычно записываются
по возрастанию. Зная значения
и , можно записать функцию распределения дискретной случайной величины в виде:
Слайд 23Пояснения по функции распределения
Это следует из определения функции распределения. Действительно,
предположим, что .
Тогда левее числа на числовой оси окажутся только те значения случайной величины, которые имеют индекс 1, 2, ..., i. Поэтому неравенство выполняется, если , . Таким образом, событие наступит, если наступит одно из событий Так как эти события несовместны, то по теореме сложения вероятностей имеемИз свойств 1 и 6 следует, что функция распределения любой дискретной случайной величины в точках разрывна, возрастает скачками, причём величина скачка равна
Слайд 24Примеры:
Пример1: Пусть - число успехов в серии из
n испытаний Бернулли. Тогда её функция распределения:
Пример 2: Если распределена
по закону Пуассона, то её функция распределения Слайд 25Пример определения функции распределения д.с.в.
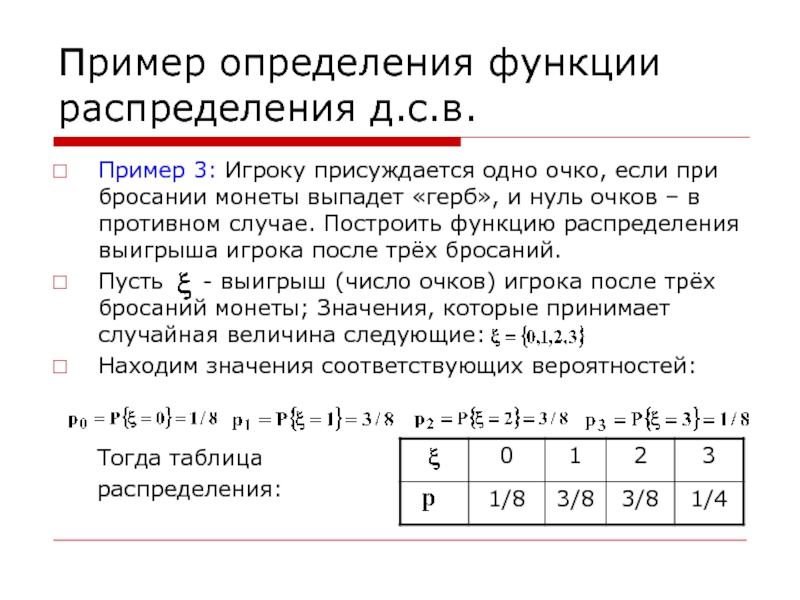
Пример 3: Игроку присуждается одно очко,
если при бросании монеты выпадет «герб», и нуль очков –
в противном случае. Построить функцию распределения выигрыша игрока после трёх бросаний.Пусть - выигрыш (число очков) игрока после трёх бросаний монеты; Значения, которые принимает случайная величина следующие:
Находим значения соответствующих вероятностей:
Тогда таблица
распределения:
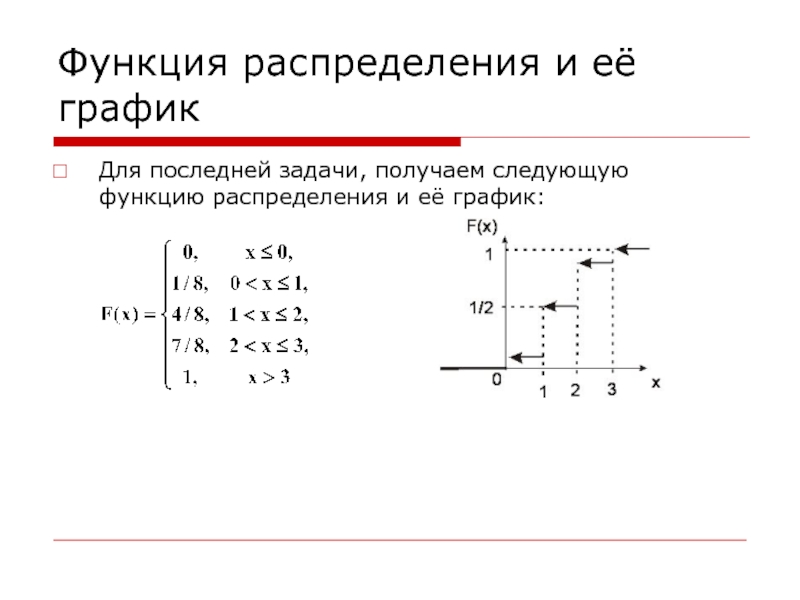
Слайд 26Функция распределения и её график
Для последней задачи, получаем следующую функцию
распределения и её график:
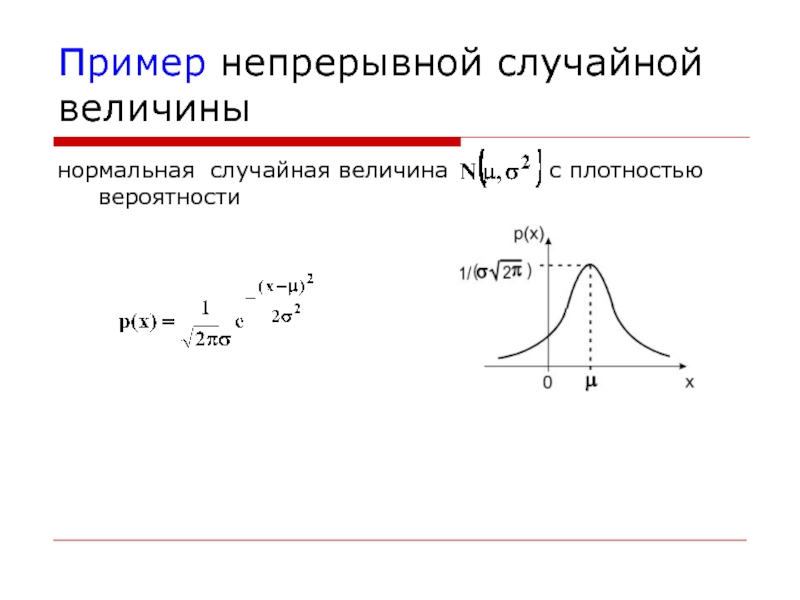
Слайд 27Непрерывная случайная величина
Случайная величина называется непрерывной, если существует
такая неотрицательная, интегрируемая на числовой прямой функция
, что её функция распределения определяетсяФункция , называется плотностью вероятности случайной величины .
Слайд 28свойства плотности вероятности
Исходя из свойства 1 функции распределения:
Вероятность того,
что принимает фиксированное значение из R, равно нулю, т.е.
.Из определения и свойства 4 функции распределения следует
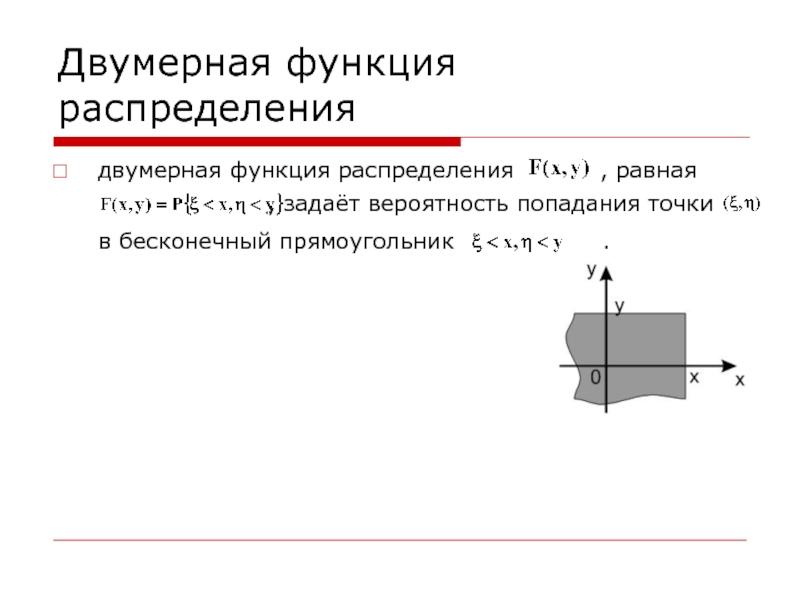
Слайд 30Двумерная функция распределения
двумерная функция распределения
, равная
, задаёт вероятность попадания точки в бесконечный прямоугольник . Слайд 31Свойства двумерной функции распределения
Функция распределения удовлетворяет неравенству:
не убывает по и
непрерывная слева по каждому аргументу4.
5.
6.
Слайд 32Дискретный и непрерывный случайный вектор
Случайный вектор называется дискретным, если каждая
его координата – дискретная случайная величина, и непрерывным, если существует
такая неотрицательная, интегрируемая на плоскости функция , называемая двумерной плотностью вероятности, чтоДискретная случайная
величина может быть
задана следующей
таблицей распределения