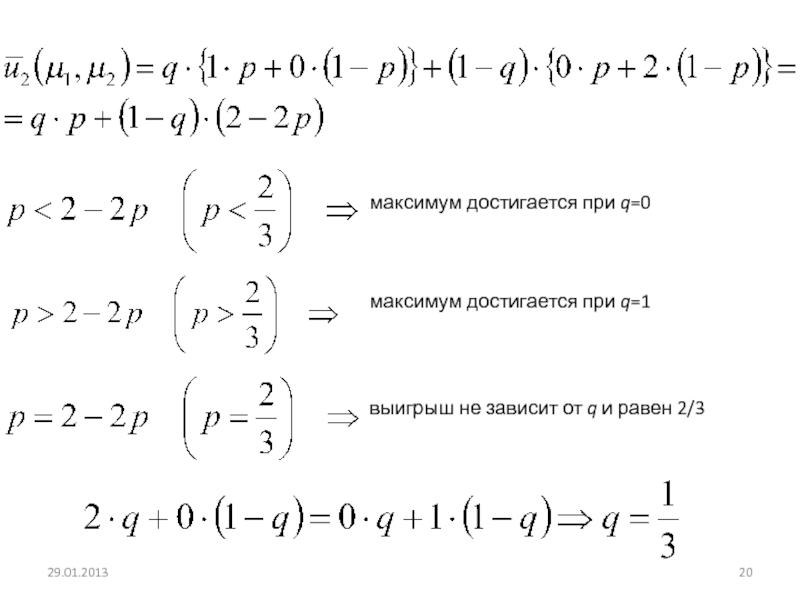Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 4 Равновесие Нэша и смешанные стратегии
Содержание
- 1. Лекция 4 Равновесие Нэша и смешанные стратегии
- 2. Существование равновесий Нэша и смешанные стратегии
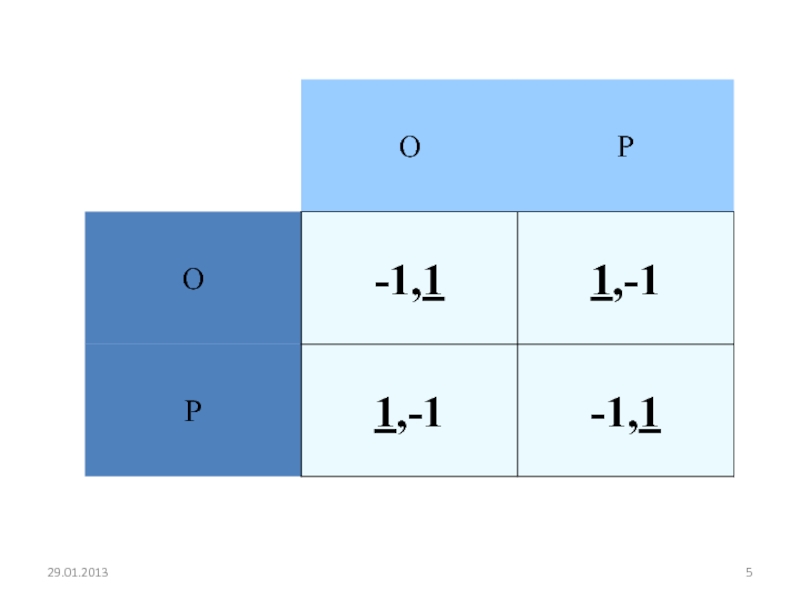
- 3. Игра «Совпадение монет»Два игрока одновременно и независимо
- 4. Слайд 4
- 5. Слайд 5
- 6. Очевидно, что ни одна из клеток не
- 7. Но в некоторых играх естественно ввести в
- 8. Обозначим множество смешанных стратегий i-го игрока
- 9. Ожидание рассчитывается в предположении, что игроки
- 10. Набор смешанных стратегий
- 11. Определение. Игра называется антагонистической, если в ней
- 12. Утверждение:Теорема. В антагонистической игре РН существует тогда
- 13. Определение. Смешанная стратегия игрока i – это
- 14. Определение. Смешанным расширением игры в нормальной форменазывается
- 15. Определение. РН в смешанных стратегиях μ* называют РН в смешанном расширении Gm:
- 16. Слайд 16
- 17. Функция отклика (наилучшего ответа) первого игрока на действия второго:
- 18. Функция отклика (наилучшего ответа) второго игрока на действия первого:
- 19. Игра «Семейный спор»:максимум достигается при р=0максимум достигается при р=1выигрыш не зависит от р и равен 2/3
- 20. максимум достигается при q=0максимум достигается при q=1выигрыш не зависит от q и равен 2/3
- 21. Функция отклика (наилучшего ответа) первого игрока на
- 22. Слайд 22
- 23. «Дилемма заключенного»:
- 24. Теорема Нэша. Пусть в игремножества стратегий Si
- 25. Вычисление РН в смешанных стратегиях
- 26. Скачать презентанцию
Существование равновесий Нэша и смешанные стратегии
Слайды и текст этой презентации
Слайд 6Очевидно, что ни одна из клеток не может быть равновесием
Нэша, поскольку ни в одной из клеток не подчеркнуты одновременно
оба выигрыша. В подобной игре каждый игрок заинтересован в том, чтобы его партнер не смог угадать, какую именно стратегию он выбрал. Этого можно достичь, внеся в выбор стратегии элемент неопределенности. Те стратегии, которые мы рассматривали ранее, принято называть чистыми стратегиями.Слайд 7Но в некоторых играх естественно ввести в рассмотрение также смешанные
стратегии. Под смешанной стратегией понимают распределение вероятностей на чистых стратегиях.
В
частном случае, когда множество чистых стратегий каждого игрока конечно, Xi = {x1i , . . . , xni i } (соответствующая игра называется конечной), смешанная стратегия представляется вектором вероятностей соответствующих чистых стратегий: μi = (μ1i, . . . , μni i ).Слайд 8Обозначим множество смешанных стратегий i-го игрока через Mi:
Стандартное
предположение теории игр состоит в том, что если выигрыш—случайная величина,
то игроки предпочитают действия, которые приносят им наибольший ожидаемый выигрыш.Ожидаемый выигрыш i-го игрока, соответствующий набору смешанных стратегий всех игроков (μ1, . . . , μm), вычисляется по формуле: