Основы геометрии. Треугольники

Содержание

1. Основы геометрии. Треугольники
2. Виды углов
3. Свойства угловСмежные углы – два угла, у
4. Смежными углами могут быть 2-3 и более углов! Все они в сумме будут 180 градусов.Если
5. Слайд 5
6. ТреугольникиТреугольник – это фигура, у которой три
7. Виды треугольников по угламОСТРОУГОЛЬНЫЙВсе углы острые (меньше
8. Виды треугольников по сторонамРАЗНОСТОРОННИЙ Все стороны и
9. Линии в треугольникеДелит угол, из которого выходит
10. Высоты в разных треугольникахВ остроугольном треугольнике все
11. Площадь треугольникаПлощадь любого треугольника ищется путем умножения
12. Равнобедренный треугольникРавные стороны называют боковыми, а неравную
13. Равносторонний треугольникВсе стороны и углы равны.При чем
14. Медиана высота и биссектриса в разных треугольникахАCBHDMВ
15. В равнобедренном треугольнике медиана, биссектриса и высота
16. Прямоугольный треугольникБольшая сторона (АВ) – гипотенуза, а
17. Свойства прямоугольного треугольникаТеорема Пифагора:
18. Слайд 18
19. Свойства прямоугольного треугольникаЕсли в прямоугольно треугольнике есть
20. Свойства прямоугольного треугольникаSin α = cos βSin β = cos α
21. Пример1086АВСsinA = 6/10 = 0,6cosA = 8/10
22. Слайд 22
23. Слайд 23
24. Скачать презентанцию

Виды углов

Главная
Разное
Основы геометрии. Треугольники

Слайды и текст этой презентации

Слайд 1Основы геометрии. Треугольники

Слайд 2Виды углов

Слайд 3Свойства углов
Смежные углы – два угла, у которых одна сторона

общая, а две другие продолжения друг друга.
Сумма смежных углов равна

180.

Вертикальные углы – углы, образованные пересечением двух прямых, и лежащие напротив друг друга. Вертикальные углы равны.

При этом

смежные

Слайд 4Смежными углами могут быть 2-3 и более углов! Все они

в сумме будут 180 градусов.
Если

Если

Слайд 5

= 40 (т.к.

вертикальные

Слайд 6Треугольники
Треугольник – это фигура, у которой три стороны, три угла

и три вершины.

Сумма всех углов любого треугольника равна 180 градусам!

Треугольники

можно разделить по:
углам;
сторонам.

ТреугольникиТреугольник – это фигура, у которой три стороны, три угла и три вершины.Сумма всех углов любого треугольника

Слайд 7Виды треугольников по углам
ОСТРОУГОЛЬНЫЙ
Все углы острые (меньше 90)
ТУПОУГОЛЬНЫЙ
Один угол тупой

(больше 90) и 2 острых (меньше 90)
ПРЯМОУГОЛЬНЫЙ Один угол прямой (равен

90) и 2 острых (меньше 90)

Слайд 8Виды треугольников по сторонам
РАЗНОСТОРОННИЙ
Все стороны и углы разные
РАВНОБЕДРЕННЫЙ
Две стороны

(боковые) равны, а другая (основание) – нет. При этом углы

напротив равных сторон тоже будут равны.

РАВНОСТОРОННИЙ
Все стороны и углы равны.
При чем каждый угол будет по 60 (т.к. в сумме все углы в треугольнике должны быть 180).

Виды треугольников по сторонамРАЗНОСТОРОННИЙ Все стороны и углы разныеРАВНОБЕДРЕННЫЙДве стороны (боковые) равны, а другая (основание) – нет.

Слайд 9Линии в треугольнике
Делит угол, из которого выходит пополам
Образует прямой (90)

угол.
Зачастую используется для нахождения площади треугольника или для образования прямоугольного

треугольника.

Делит сторону, которую пересекает пополам (на равные части).

Линии в треугольникеДелит угол, из которого выходит пополамОбразует прямой (90) угол.Зачастую используется для нахождения площади треугольника или

Слайд 10Высоты в разных треугольниках
В остроугольном треугольнике все три высоты находятся

внутри треугольника. Высоты для сторон:
СН2 - высота для стороны АВ
АН1

- высота для стороны ВС
ВН3 - высота для стороны АС

В тупоугольном треугольнике две высоты находятся снаружи (они опускаются на продолжение сторон) треугольника, а одна - внутри. Высоты для сторон:
СF - высота для стороны АВ
АD - высота для стороны ВС
ВE - высота для стороны АС

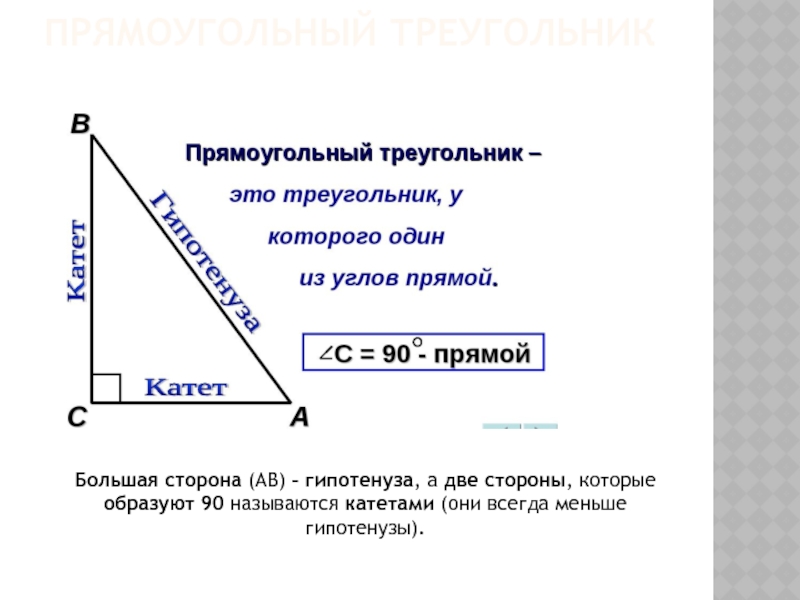
В прямоугольном треугольнике две высоты – это сами стороны треугольника (т.к. они перпендикулярны друг другу, т.е пересекаются уже под углом 90), а одна высота находится внутри. Высоты для сторон:
СK - высота для стороны АB
АC - высота для стороны ВС
CB - высота для стороны АС

Высоты в разных треугольникахВ остроугольном треугольнике все три высоты находятся внутри треугольника. Высоты для сторон:СН2 - высота

Слайд 11Площадь треугольника
Площадь любого треугольника ищется путем умножения любой его стороны

на высоту, проведенную именно к этой стороне, деленную на 2.
а
h1
h2
h3
b
c
S

= (a*h1)/2

S = (b*h2)/2

S = (c*h3)/2

Площадь треугольникаПлощадь любого треугольника ищется путем умножения любой его стороны на высоту, проведенную именно к этой стороне,

Слайд 12Равнобедренный треугольник
Равные стороны называют боковыми, а неравную – основание.
Две

стороны (боковые) равны, а другая (основание) – нет.
Углы напротив

равных сторон равны.

140

Равнобедренный треугольникРавные стороны называют боковыми, а неравную – основание. Две стороны (боковые) равны, а другая (основание) –

Слайд 13Равносторонний треугольник
Все стороны и углы равны.
При чем каждый угол будет

по 60 (т.к. в сумме все углы в треугольнике должны

быть 180).

Равносторонний треугольникВсе стороны и углы равны.При чем каждый угол будет по 60 (т.к. в сумме все углы

Слайд 14Медиана высота и биссектриса в разных треугольниках
А
C
B
H
D
M
В разностороннем треугольнике:
ВМ –

медиана;
ВД – биссектриса;
ВН- высота.
Все три линии – разные!
Н
В равнобедренном треугольнике

СН - медиана, биссектриса и высота (одна и та же линия). Но только проведенные к основанию!!!

В равностороннем треугольнике ВН - медиана, биссектриса и высота (одна и та же линия). Проведенные к любой стороне!!!

Медиана высота и биссектриса в разных треугольникахАCBHDMВ разностороннем треугольнике:ВМ – медиана;ВД – биссектриса;ВН- высота.Все три линии –

Слайд 15В равнобедренном треугольнике медиана, биссектриса и высота равны (одна и

та же линия). Но только проведенные к основанию!!!
В равностороннем треугольнике

медиана, биссектриса и высота равны (одна и та же линия). Проведенные к любой стороне!!!

В равнобедренном треугольнике медиана, биссектриса и высота равны (одна и та же линия). Но только проведенные к

Слайд 16Прямоугольный треугольник
Большая сторона (АВ) – гипотенуза, а две стороны, которые

образуют 90 называются катетами (они всегда меньше гипотенузы).

Прямоугольный треугольникБольшая сторона (АВ) – гипотенуза, а две стороны, которые образуют 90 называются катетами (они всегда меньше

Слайд 17Свойства прямоугольного треугольника
Теорема Пифагора:

Слайд 18

Слайд 19Свойства прямоугольного треугольника
Если в прямоугольно треугольнике есть угол равный 30

градусам, то напротив него лежит катет, который будет в два

раза меньше гипотенузы.

Свойства прямоугольного треугольникаЕсли в прямоугольно треугольнике есть угол равный 30 градусам, то напротив него лежит катет, который

Слайд 20Свойства прямоугольного треугольника
Sin α = cos β
Sin β = cos

Свойства прямоугольного треугольникаSin α = cos βSin β = cos α

Слайд 21Пример
10
8
6
А
В
С
sinA = 6/10 = 0,6
cosA = 8/10 = 0,8
tgA =

6/8 = 0,75

sinB = 8/10 = 0,8
cosB = 6/10 =

0,6
tgB = 8/6 = 4/3

Пример1086АВСsinA = 6/10 = 0,6cosA = 8/10 = 0,8tgA = 6/8 = 0,75sinB = 8/10 = 0,8cosB

Слайд 22

Слайд 23

Скачать презентацию

Разделы презентаций

Основы геометрии. Треугольники

Содержание

Слайды и текст этой презентации

Слайд 1Основы геометрии. Треугольники

Слайд 2Виды углов

Слайд 3Свойства угловСмежные углы – два угла, у которых одна сторона

общая, а две другие продолжения друг друга.Сумма смежных углов равна

Слайд 4Смежными углами могут быть 2-3 и более углов! Все они

в сумме будут 180 градусов.Если

Слайд 5

= 40 (т.к.

Слайд 6ТреугольникиТреугольник – это фигура, у которой три стороны, три угла

и три вершины.Сумма всех углов любого треугольника равна 180 градусам!Треугольники

Слайд 7Виды треугольников по угламОСТРОУГОЛЬНЫЙВсе углы острые (меньше 90)ТУПОУГОЛЬНЫЙОдин угол тупой

(больше 90) и 2 острых (меньше 90)ПРЯМОУГОЛЬНЫЙ Один угол прямой (равен

Слайд 8Виды треугольников по сторонамРАЗНОСТОРОННИЙ Все стороны и углы разныеРАВНОБЕДРЕННЫЙДве стороны

(боковые) равны, а другая (основание) – нет. При этом углы

Слайд 9Линии в треугольникеДелит угол, из которого выходит пополамОбразует прямой (90)

угол.Зачастую используется для нахождения площади треугольника или для образования прямоугольного

Слайд 10Высоты в разных треугольникахВ остроугольном треугольнике все три высоты находятся

внутри треугольника. Высоты для сторон:СН2 - высота для стороны АВАН1

Слайд 11Площадь треугольникаПлощадь любого треугольника ищется путем умножения любой его стороны

на высоту, проведенную именно к этой стороне, деленную на 2.аh1h2h3bcS

Слайд 12Равнобедренный треугольникРавные стороны называют боковыми, а неравную – основание. Две

стороны (боковые) равны, а другая (основание) – нет. Углы напротив

Слайд 13Равносторонний треугольникВсе стороны и углы равны.При чем каждый угол будет