Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 5
Содержание
- 1. Лекция 5
- 2. Методы одномерной оптимизации
- 3. К методам одномерной оптимизации относятся: метод дихотомического
- 4. На отрезке [A,B] имеется один минимум (в
- 5. На следующем шаге вместо отрезка [A,B] нужно
- 6. По методу золотого сечения внутри отрезка [A,B]
- 7. Следовательно, вместо отрезка [A,B] теперь можно рассматривать
- 8. Условие получения такого значения а:
- 9. Таким образом, требуется не более N шагов
- 10. Согласно методу чисел Фибоначчи, используют числа Фибоначчи
- 11. Метод аналогичен методу золотого сечения с тем
- 12. Например, если (В-А)/Е=100, то начальное значение i
- 13. По методу полиномиальной аппроксимации при аппроксимации F(x)
- 14. В результате становятся известными значения коэффициентов аk
- 15. Методы безусловной оптимизации
- 16. Среди методов нулевого порядка в САПР находят
- 17. Метод Розенброка является улучшенным вариантом покоординатного спуска.Характеризуется
- 18. Траектория покоординатного спуска для примера двумерного пространства
- 19. При использовании метода покоординатного спуска велика вероятность
- 20. Примечание Оврагом называют часть пространства управляемых параметров,
- 21. В то же время при благоприятной ориентации
- 22. Метод Розенброка заключается в таком повороте координатных
- 23. Другой модификацией покоординатного спуска является метод конфигураций.
- 24. Поиск экстремума методом деформируемого многогранника основан на
- 25. Эти правила поясняются рисунком на примере двумерной
- 26. Если оказывается, что X4 имеет лучшее значение
- 27. Если новая вершина окажется худшей, то в
- 28. Случайные методы поиска характеризуются тем, что направления поиска g выбирают случайным образом.
- 29. Особенностью метода наискорейшего спуска является выполнение шагов
- 30. При использовании метода наискорейшего спуска, как и
- 31. Чтобы повысить эффективность градиентных методов используют различные
- 32. Векторы А и В называют Q-сопряженными, если
- 33. Особенность сопряженных направлений для Q = Г,
- 34. Примечание Матрицей Гессе называют матрицу вторых частных
- 35. Пример Поиск экстремума выполняют в соответствии с
- 36. Поскольку шаг h рассчитывается исходя из условия
- 37. Алгоритм поиска сводится к применению формулыпока не будет выполнено условие окончания вычислений
- 38. Чтобы определить коэффициент wi решают систему уравнений путем подстановки величин Si+1 и Si из соответствующих уравнений.
- 39. или откуда и с учетом
- 40. Следовательно, На первом шаге поиска выбирают S1=-grad
- 41. Метод переменной метрики (метод Девидона – Флетчера
- 42. Выражение grad F(X)=0 представляет собой систему алгебраических
- 43. Выражение — это система линейных алгебраических уравнений.
- 44. Главный недостаток метода — высокая трудоемкость вычисления
- 45. Введем обозначения: E — единичная матрица. Начальное
- 46. Поэтому Можно показать, что Ai стремится к
- 47. Спасибо за внимание!
- 48. Скачать презентанцию
Методы одномерной оптимизации
Слайды и текст этой презентации
Слайд 3К методам
одномерной оптимизации относятся:
метод дихотомического деления,
метод золотого
сечения,
Слайд 4
На отрезке [A,B] имеется один минимум
(в общем случае нечетное
число минимумов).
Согласно методу дихотомического деления отрезок делят пополам и
в точках, отстоящих от центра С отрезка на величину допустимой погрешности q, рассчитывают значения целевой функции F(C+q) и F(C-q). Если окажется, что F(C+q) > F(C-q), то минимум находится на отрезке [A,C], если F(C+q)< F(C-q), то минимум — на [C,B], если
F(C+q) =F(C-q) — на [C-q,C+q]
![На отрезке [A,B] имеется один минимум (в общем случае нечетное число минимумов). Согласно методу дихотомического деления отрезок](/img/tmb/7/639901/43c3455cb6d476c7448a1683d1cf1082-800x.jpg "Лекция 5 На отрезке [A,B] имеется один минимум (в общем случае нечетное число")
Слайд 5На следующем шаге вместо отрезка [A,B] нужно исследовать суженный отрезок
[A,C], [C,B] или [C-q,C+q].
Шаги повторяются, пока длина отрезка не
уменьшится до величины погрешности q. Таким образом, требуется
не более N шагов,
где N — ближайшее к log((B-A)/q)
целое значение,
но на каждом шаге целевую функцию следует вычислять дважды.
![На следующем шаге вместо отрезка [A,B] нужно исследовать суженный отрезок [A,C], [C,B] или [C-q,C+q]. Шаги повторяются, пока](/img/tmb/7/639901/3940431ffaaa73ba02e6ebc1aefce1a6-800x.jpg "Лекция 5 На следующем шаге вместо отрезка [A,B] нужно исследовать суженный отрезок [A,C],")
Слайд 6
По методу золотого сечения внутри отрезка [A,B] выделяют две промежуточные
точки С1 и D1 на расстоянии s = aL от
его конечных точек,где L = B-A — длина отрезка.
Затем вычисляют значения целевой функции F(x) в точках С1 и D1.
Если F(C1) < F(D1), то минимум находится на отрезке [A,D1], если F(C1) > F(D1)),
то — на отрезке [C1,B], если
F(C1) = F(D1) — на отрезке [ C1, D1].
![По методу золотого сечения внутри отрезка [A,B] выделяют две промежуточные точки С1 и D1 на расстоянии s](/img/tmb/7/639901/dc6fc117240ff439750af01cf790e05c-800x.jpg "Лекция 5 По методу золотого сечения внутри отрезка [A,B] выделяют две промежуточные точки")
Слайд 7Следовательно, вместо отрезка [A,B] теперь можно рассматривать
отрезок [A,D1], [C1,B]
или [C1, D1],
т.е. длина отрезка уменьшилась не менее чем
в L/(L-aL) = 1/(1-a) раз. Если подобрать значение a так, что в полученном отрезке меньшей длины одна из промежуточных точек совпадет с промежуточной точкой от предыдущего шага,
т.е. в случае выбора отрезка [A,D1] точка D2 совпадет с точкой C1, а в случае выбора отрезка [C1,B] точка C2 — с точкой D1, то это позволит сократить число вычислений целевой функции на всех шагах
(кроме первого) в 2 раза.
![Следовательно, вместо отрезка [A,B] теперь можно рассматривать отрезок [A,D1], [C1,B] или [C1, D1], т.е. длина отрезка уменьшилась](/img/tmb/7/639901/571a42614d394b23d1fe66eed74b7330-800x.jpg "Лекция 5 Следовательно, вместо отрезка [A,B] теперь можно рассматривать отрезок [A,D1], [C1,B] или")
Слайд 8Условие получения такого значения а:
откуда с учетом
имеем
а = 0,382.
Это значение
называют золотым сечением.
Слайд 9Таким образом, требуется
не более N шагов и N+1 вычислений
целевой функции,
где N можно рассчитать, используя соотношение
при заданной
погрешности Е определения экстремума. 
Слайд 10Согласно методу чисел Фибоначчи, используют числа Фибоначчи Ri, последовательность которых
образуется по правилу
при т.е. ряд чисел Фибоначчи имеет вид
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144....
Слайд 11Метод аналогичен методу золотого сечения с тем отличием, что коэффициент
а равен отношению
начальное значение i определяется из условия,
что Ri должно быть наименьшим числом Фибоначчи, превышающим величину (B-A)/E, где Е — заданная допустимая погрешность определения экстремума.
Слайд 12Например, если
(В-А)/Е=100,
то начальное значение i = 12,
поскольку
R1=144 и а=55/144=0,3819,
на следующем шаге будет
a=34/89=0,3820
и т.д. 
Слайд 13По методу полиномиальной аппроксимации
при аппроксимации F(x) квадратичным полиномом
выбирают
промежуточную точку С и в точках
А, В, С вычисляют
значения целевой функции. Далее решают систему из трех алгебраических уравнений, полученных подстановкой в уравнение квадратичного полинома значений А, В, С вместо х и вычисленных значений функции вместо Р(х).
Слайд 14В результате становятся известными значения коэффициентов аk в уравнении и,
исходя из условия
, определяют экстремальную точку Э полинома.Например, если точка С выбрана в середине отрезка [A,B], то
Слайд 16Среди методов нулевого порядка
в САПР находят применение:
метод Розенброка,
метод
конфигураций (Хука-Дживса),
метод деформируемого многогранника (Нелдера-Мида),
метод случайного поиска.
К методам
с использованием производных относятся:метод наискорейшего спуска,
метод сопряженных градиентов,
метод переменной метрики.
Слайд 17Метод Розенброка является улучшенным вариантом покоординатного спуска.
Характеризуется выбором направлений поиска
поочередно вдоль всех n координатных осей,
шаг рассчитывается на основе
одномерной оптимизации, критерий окончания поиска |Xk -Xkn| < ε,
где ε — заданная точность определения локального экстремума,
n— размерность пространства управляемых параметров.
Слайд 18
Траектория покоординатного спуска для примера двумерного пространства управляемых параметров показана
на рисунке,
где Xk— точки на траектории поиска,
xi— управляемые
параметры. Целевая функция представлена своими линиями равного уровня, около каждой линии записано соответствующее ей значение F(X).
Точка Q есть точка минимума.
Слайд 19
При использовании метода покоординатного спуска велика вероятность «застревания» поиска на
дне оврага вдали от точки экстремума. На рисунке видно, что
после попадания в точку А, расположенную на дне оврага, дальнейшие шаги возможны лишь в направлениях aa или bb, но они приводят к ухудшению целевой функции. Следовательно, поиск прекращается в точке А.
Слайд 20Примечание
Оврагом называют часть пространства управляемых параметров, в которой наблюдаются
слабые изменения производных целевой функции по одним направлениям и значительные
изменения с переменой знака — по некоторым другим направлениям.Знак производной меняется в точках, принадлежащих дну оврага.
Слайд 21
В то же время при благоприятной ориентации дна оврага, а
именно при положении одной из координатных осей, близком к параллельности
с дном оврага, поиск оказывается весьма быстрым. Эта ситуация показана на рисунке.
Слайд 22
Метод Розенброка заключается в таком повороте координатных осей, чтобы одна
из них оказалась квазипараллельной дну оврага. Такой поворот осуществляют на
основе данных, полученных после серии из n шагов покоординатного спуска.Положение новых осей si может быть получено линейным преобразованием прежних осей xi: ось s1 совпадает по направлению с вектором Xk+n-Xk; остальные оси выбирают из условия ортогональности к N1 и друг к другу.
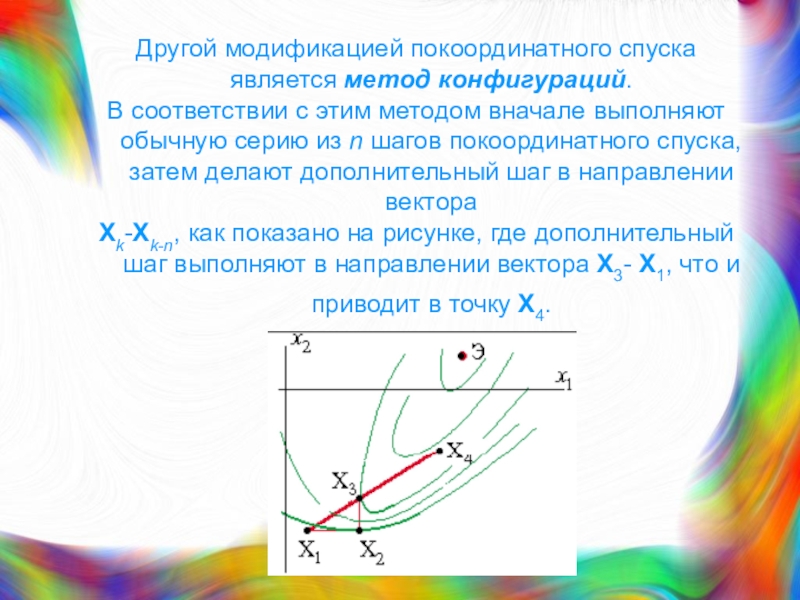
Слайд 23Другой модификацией покоординатного спуска является метод конфигураций.
В соответствии с
этим методом вначале выполняют обычную серию из n шагов покоординатного
спуска, затем делают дополнительный шаг в направлении вектораXk-Xk-n, как показано на рисунке, где дополнительный шаг выполняют в направлении вектора X3- X1, что и приводит в точку X4.
Слайд 24
Поиск экстремума методом деформируемого многогранника основан на построении многогранника
с
(n +1) вершинами на каждом шаге поиска,
где n— размерность
пространства управляемых параметров. В начале поиска эти вершины выбирают произвольно, на последующих шагах выбор подчинен правилам метода.
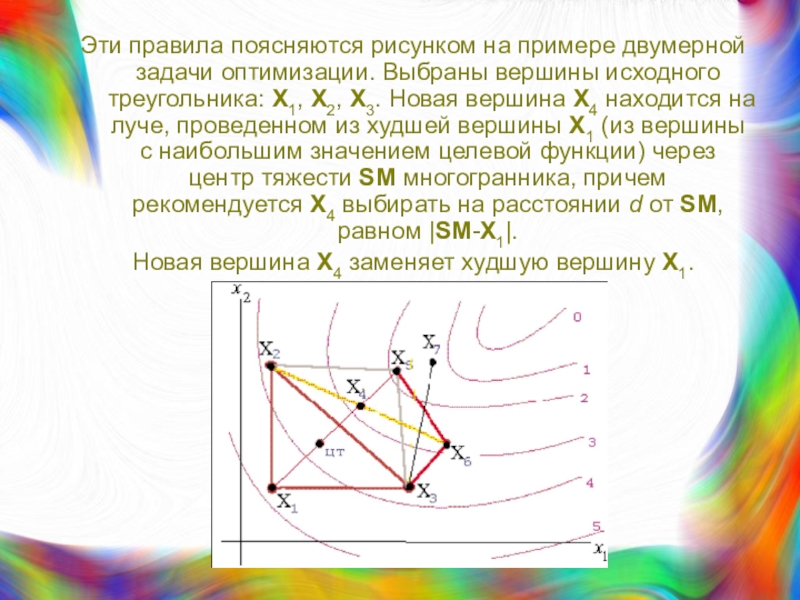
Слайд 25Эти правила поясняются рисунком на примере двумерной задачи оптимизации. Выбраны
вершины исходного треугольника: X1, X2, X3. Новая вершина X4 находится
на луче, проведенном из худшей вершины X1 (из вершины с наибольшим значением целевой функции) через центр тяжести SM многогранника, причем рекомендуется X4 выбирать на расстоянии d от SM, равном |SM-X1|.Новая вершина X4 заменяет худшую вершину X1.
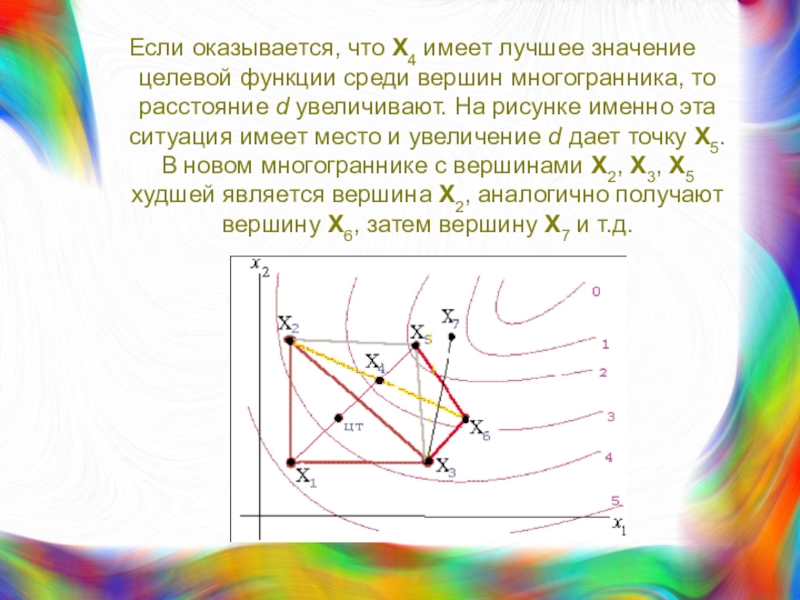
Слайд 26Если оказывается, что X4 имеет лучшее значение целевой функции среди
вершин многогранника, то расстояние d увеличивают. На рисунке именно эта
ситуация имеет место и увеличение d дает точку X5. В новом многограннике с вершинами X2, X3, X5 худшей является вершина X2, аналогично получают вершину X6, затем вершину X7 и т.д.
Слайд 27
Если новая вершина окажется худшей, то в многограннике нужно сохранить
лучшую вершину, а длины всех ребер уменьшить,
например, вдвое (стягивание
многогранника к лучшей вершине). Поиск прекращается при выполнении условия уменьшения размеров многогранника до некоторого предела.
Слайд 28
Случайные методы поиска характеризуются тем, что направления поиска g выбирают
случайным образом.
Слайд 29Особенностью
метода наискорейшего спуска
является выполнение шагов поиска в градиентном
направлении
шаг h выбирается оптимальным с помощью одномерной оптимизации.
Слайд 30При использовании метода наискорейшего спуска,
как и большинства других методов,
эффективность поиска существенно снижается в овражных ситуациях.
Траектория поиска приобретает
зигзагообразный вид с медленным продвижением вдоль дна оврага в сторону экстремума. 
Слайд 31
Чтобы повысить эффективность градиентных методов используют различные приемы.
Один из
таких приемов, использованный в
методе сопряженных градиентов (методе Флетчера-Ривса),
основан
на понятии сопряженности векторов. 
Слайд 32Векторы А и В называют
Q-сопряженными, если ATQB=0,
где Q
— положительно определенная квадратная матрица того же порядка, что и
размер N векторов А и В(частный случай сопряженности — ортогональность векторов,
когда Q является единичной матрицей порядка N),
AT - вектор-строка, B — вектор-столбец.
Слайд 33
Особенность сопряженных направлений для Q = Г, где Г —
матрица Гессе, в задачах с квадратичной целевой функцией F(X) заключается
в следующем:одномерная минимизация F(X) последовательно по N сопряженным направлениям позволяет найти экстремальную точку не более, чем за N шагов.
Слайд 34Примечание
Матрицей Гессе называют матрицу вторых частных производных целевой функции
по управляемым параметрам.
Основанием для использования поиска по Г -
сопряженным направлениям является то, что для функций F(X) общего вида может быть применена квадратичная аппроксимация, что на практике выливается в выполнение поиска более, чем за N шагов. 
Слайд 35Пример
Поиск экстремума выполняют в соответствии
с формулой
Направление Si+1 поиска
на очередном шаге связано с направлением поиска Si на предыдущем
шаге соотношениемгде wi — коэффициент.
Кроме того, учитывают условие сопряженности
и линейную аппроксимацию gradF(X) в окрестностях точки Хi
Слайд 36Поскольку шаг h рассчитывается исходя из условия одномерной оптимизации, то,
во-первых, справедливо соотношение
во-вторых, имеем
откуда получаем
Слайд 37
Алгоритм поиска сводится к применению формулы
пока не будет выполнено условие
окончания вычислений
Слайд 38Чтобы определить коэффициент wi решают систему уравнений
путем подстановки величин
Si+1 и Si из соответствующих уравнений.
Слайд 40Следовательно,
На первом шаге поиска выбирают
S1=-grad F(X0) и находят
точку X1.
На втором шаге по формуле рассчитывают w1, по
соответствующим формулам определяют S2 и X2 и т.д.
Слайд 41Метод переменной метрики
(метод Девидона – Флетчера - Пауэлла) можно
рассматривать как результат усовершенствования метода второго порядка — метода Ньютона.
Метод Ньютона основан на использовании необходимых условий безусловного экстремума целевой функции F(X)
grad F(X)=0.
Слайд 42Выражение grad F(X)=0 представляет собой систему алгебраических уравнений, для решения
которой можно применить известный численный метод, называемый методом Ньютона.
Корень
этой системы есть стационарная точка, т.е. возможное решение экстремальной задачи.
Метод Ньютона является итерационным, он основан на линеаризации grad F(X)=0 в окрестности текущей точки поиска Хk
Слайд 43Выражение
— это система линейных алгебраических уравнений.
Ее корень есть
очередное приближение Хk+1 к решению
Если процесс сходится, то
решение достигается за малое число итераций, окончанием которых служит выполнение условия 
Слайд 44Главный недостаток метода — высокая трудоемкость вычисления и обращения матрицы
Г, к тому же ее вычисление численным дифференцированием сопровождается заметными
погрешностями, что снижает скорость сходимости.В методе переменной метрики вместо трудно вычисляемой обратной матрицы Гессе используют некоторую более легко вычисляемую матрицу N, т.е.
Слайд 45Введем обозначения:
E — единичная матрица.
Начальное значение матрицы N0
= E. Матрицу N корректируют на каждом шаге, т.е.
где
Слайд 46Поэтому
Можно показать, что Ai стремится к Г-1, Вi —
к E при k→n,
где n — размерность пространства управляемых
параметров. Спустя n шагов, нужно снова начинать с Nn+1 = E.
