Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 5. Корпускулярно – волновой дуализм. Квантовое состояние. Уравнение
Содержание
- 1. Лекция 5. Корпускулярно – волновой дуализм. Квантовое состояние. Уравнение
- 2. 1.Корпускулярно-волновой дуализм свойств вещества.
- 3. Корпускулярные характеристики - энергия и импульс
- 4. 2. Некоторые свойства волн де Бройля.
- 5. Групповая скорость волн де БройляФазовая скорость волн
- 6. 3. Соотношение неопределенностей.
- 7. Соотношение неопределенностей Гейзенберга: Микрочастица не может иметь
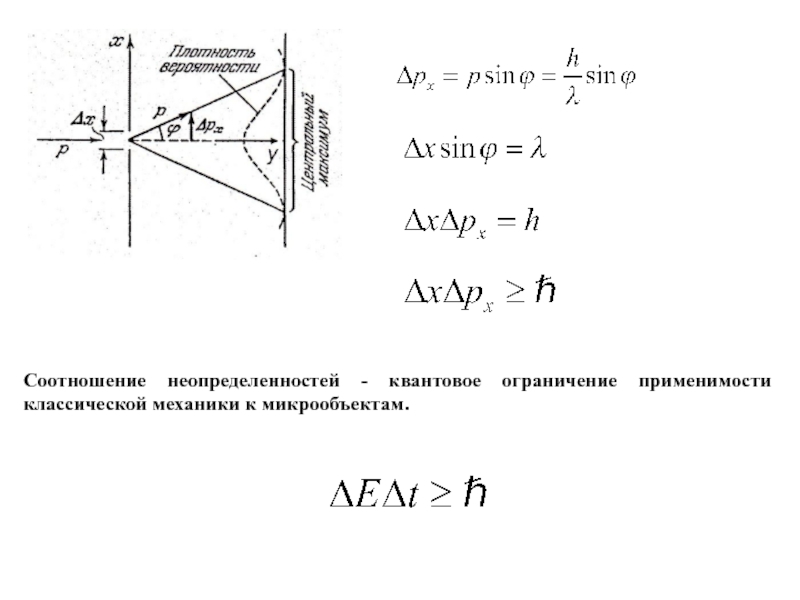
- 8. Соотношение неопределенностей - квантовое ограничение применимости классической механики к микрообъектам.
- 9. 4. Волновая функция и ее свойства.
- 10. Для описания поведения квантовых систем вводится волновая функция (пси-функция) Условие нормировки вероятностей
- 11. Волновая функция, характеризующая вероятность обнаружения действия микрочастицы
- 12. 5.Общее уравнение Шредингера.
- 13. Нестационарное (временное) уравнение Шредингера имеет видмасса частицы
- 14. Уравнение дополняется условиями, накладываемыми на волновую функцию:1)
- 15. 6.Уравнение Шредингера для стационарных состояний.
- 16. Уравнение Шредингера для стационарных состояний оператор Лапласа
- 17. 7. Движение свободной частицы.
- 18. Свободной называется частица, не подверженная действию силовых полей. Это значит, что
- 19. 8. Частица в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками».
- 20. при
- 21. Таким образом, энергия частицы в бесконечно высокой
- 22. Собственные волновые функцииНа рисунке изображены графики собственных
- 23. 9. Прохождение частицы через потенциальный барьер. Туннельный эффект.
- 24. Слайд 24
- 25. Квантовая механика приводит к новому квантовому явлению,
- 26. 10. Линейный гармонический осциллятор в квантовой механике.
- 27. Линейный гармонический осциллятор - система, совершающая одномерное
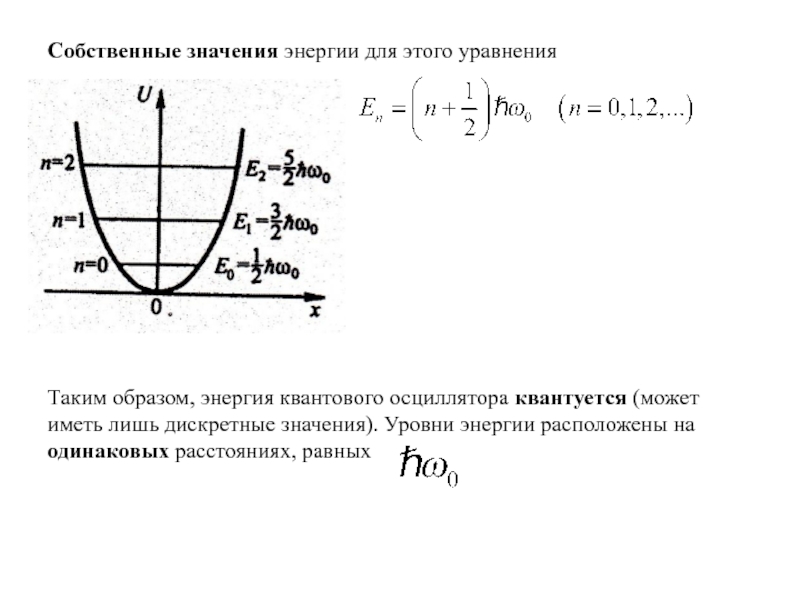
- 28. Собственные значения энергии для этого уравнения
- 29. Минимальная энергия
- 30. 11. Движение электрона в водородоподобном атоме
- 31. Уравнение Шредингера
- 32. Слайд 32
- 33. Слайд 33
- 34. Слайд 34
- 35. Слайд 35
- 36. Слайд 36
- 37. Слайд 37
- 38. Слайд 38
- 39. Слайд 39
- 40. Слайд 40
- 41. Скачать презентанцию
1.Корпускулярно-волновой дуализм свойств вещества.
Слайды и текст этой презентации
Слайд 1Лекция 5.
Корпускулярно – волновой дуализм.
Квантовое состояние. Уравнение Шредингера.
Доцент
Кравцова О.С.
Слайд 3Корпускулярные характеристики - энергия и импульс Волновые характеристики - частота
и длина волны . Соотношения между корпускулярными и волновыми характеристиками частиц
: Таким образом, любой частице, обладающей импульсом (в том числе и частице, в отличие от фотона, обладающей массой покоя), сопоставляется волновой процесс с длиной волны, определяемой по формуле де Бройля
Слайд 5Групповая скорость волн де Бройля
Фазовая скорость волн де Бройля
Волны
де Бройля перемещаются вместе с частицей
Для фотона
Слайд 7Соотношение неопределенностей Гейзенберга: Микрочастица не может иметь одновременно определенную координату
и определенную соответствующую
проекцию импульса , причем неопределенности этих величин удовлетворяют соотношениям т.е. произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядка .
Слайд 8Соотношение неопределенностей - квантовое ограничение применимости классической механики к микрообъектам.
Слайд 10Для описания поведения квантовых систем вводится волновая функция (пси-функция)
Условие
нормировки вероятностей
Слайд 11Волновая функция, характеризующая вероятность обнаружения действия микрочастицы в элементе объёма
должна быть: 1) конечной (вероятность не может быть больше единицы), 2) однозначной
(вероятность не может быть неоднозначной величиной) 3) непрерывной (вероятность не может изменяться скачком). Волновая функция позволяет вычислить средние значения физических величин, характеризующих данный микрообъект. Волновая функция удовлетворяет принципу суперпозиции:
Слайд 13Нестационарное (временное) уравнение Шредингера имеет вид
масса частицы
постоянная Планка
оператор
Лапласа
мнимая единица
потенциальная функция частицы в силовом поле, в
котором она движется (функция не только пространственных координат, но и времениискомая волновая функция частицы
Слайд 14Уравнение дополняется условиями, накладываемыми на волновую функцию:
1) волновая функция должна
быть конечной, однозначной и непрерывной;
2) производные
должны быть непрерывны;
3)
функция должна быть интегрируема; это условие в простейших случаях сводится к условию нормировки вероятностей.
Слайд 16Уравнение Шредингера для стационарных состояний
оператор Лапласа
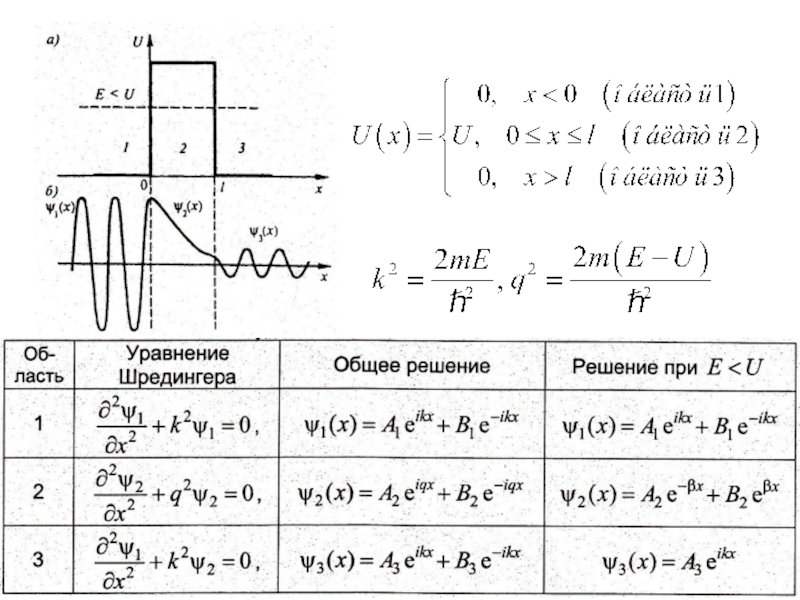
Описывает поведение квантовой
частицы в стационарном (не изменяющемся со временем) потенциальном поле Решением
является комплексная волновая функция
Слайд 21Таким образом, энергия частицы в бесконечно высокой потенциальной «яме» принимает
лишь определенные дискретные значения, т.е. квантуется. Квантованные значения энергии
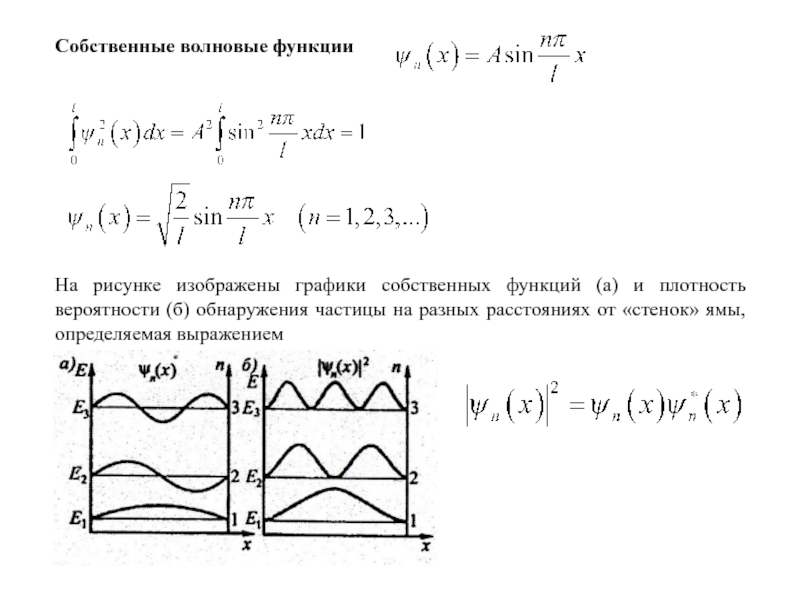
называются уровнями энергии, а число , определяющее энергетические уровни частицы называется главным квантовым числом.
Слайд 22Собственные волновые функции
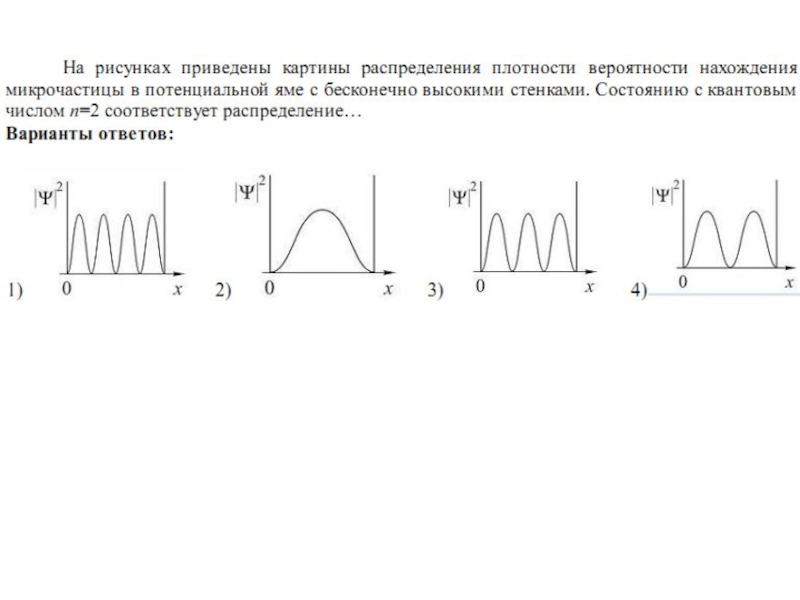
На рисунке изображены графики собственных функций (а) и
плотность вероятности (б) обнаружения частицы на разных расстояниях от «стенок»
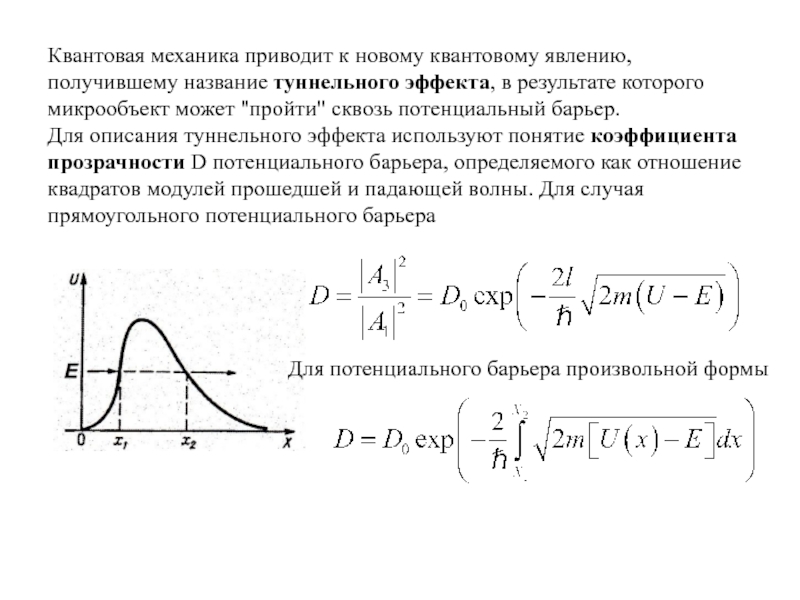
ямы, определяемая выражением
Слайд 25Квантовая механика приводит к новому квантовому явлению, получившему название туннельного
эффекта, в результате которого микрообъект может "пройти" сквозь потенциальный барьер. Для
описания туннельного эффекта используют понятие коэффициента прозрачности D потенциального барьера, определяемого как отношение квадратов модулей прошедшей и падающей волны. Для случая прямоугольного потенциального барьераДля потенциального барьера произвольной формы
Слайд 27Линейный гармонический осциллятор - система, совершающая одномерное движение под действием
квазиупругой силы. Потенциальная энергия гармонического осциллятора равна Уравнение Шредингера для стационарных состояний
квантового осциллятора
Слайд 28Собственные значения энергии для этого уравнения Таким образом, энергия квантового осциллятора
квантуется (может иметь лишь дискретные значения). Уровни энергии расположены на
одинаковых расстояниях, равных
Слайд 29Минимальная энергия
называется энергией нулевых колебаний. Для гармонического осциллятора возможны лишь переходы между
соседними подуровнями, т.е. переходы, удовлетворяющие правилу отбора Следовательно, энергия гармонического осциллятора может изменяться только порциями и гармонический осциллятор испускает и поглощает энергию квантами.
