TheSlide.ru

Лекция 5 Обобщенная модель нейрона. Персептрон (структура, алгоритмы

Содержание

1. Лекция 5 Обобщенная модель нейрона. Персептрон (структура, алгоритмы
2. в противном случае.1943 – формальный нейрон (МакКаллок,
3. ПРОБЛЕМА ИСКЛЮЧАЮЩЕГО ИЛИ (Exclusive OR, XOR)→ [М. Мински, С. Пейперт, 1969]Таблица истинности функции XOR
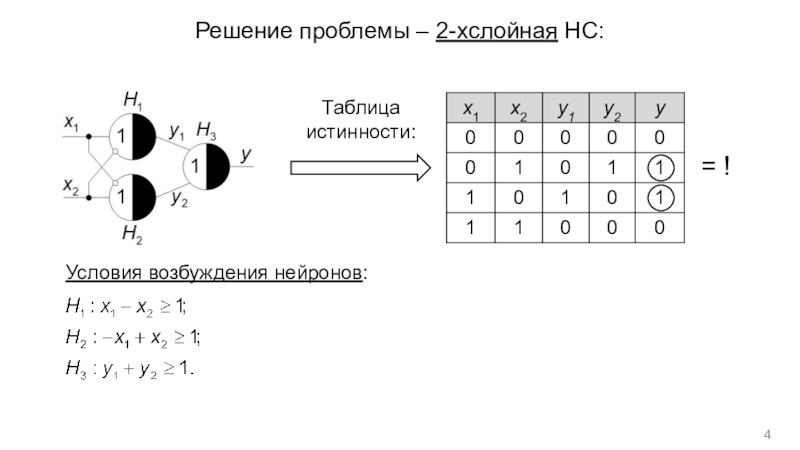
4. Решение проблемы – 2-хслойная НС:Таблица истинности:= !Условия возбуждения нейронов:
5. ОБОБЩЕННАЯ МОДЕЛЬ НЕЙРОНА
6. ВИДЫ ФУНКЦИИ АКТИВАЦИИ
7. ПЕРСЕПТРОН (структура)1958 – однослойный персептрон (Ф. Розенблат)
8. ПЕРСЕПТРОН (процедура обучения)– вектор эталонов, (желаемых выходов)
9. ОБУЧАЮЩАЯ ВЫБОРКА– это набор пар
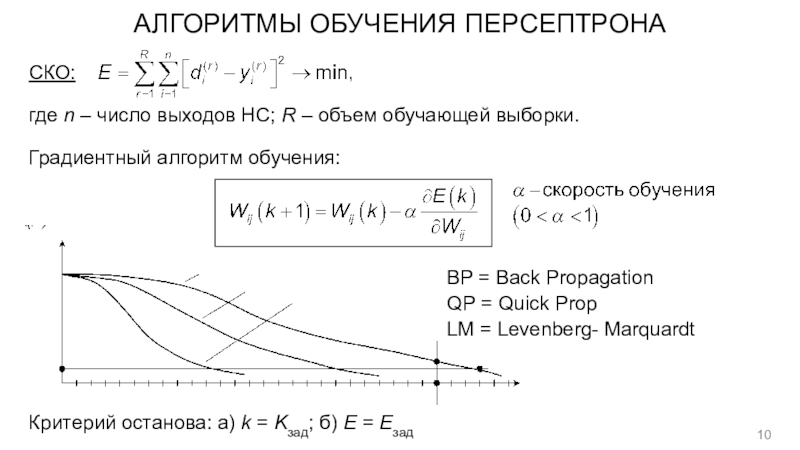
10. АЛГОРИТМЫ ОБУЧЕНИЯ ПЕРСЕПТРОНАСКО:где n – число выходов
11. СЛОЖНОСТИ ПРОЦЕССА ОБУЧЕНИЯ«зависание» в локальных минимумахметод «тяжелого»
12. РЕШЕНИЕ ЗАДАЧИ РАСПОЗНАВАНИЯ ОБРАЗОВ С ПОМОЩЬЮ ПЕРСЕПТРОНАЗадача
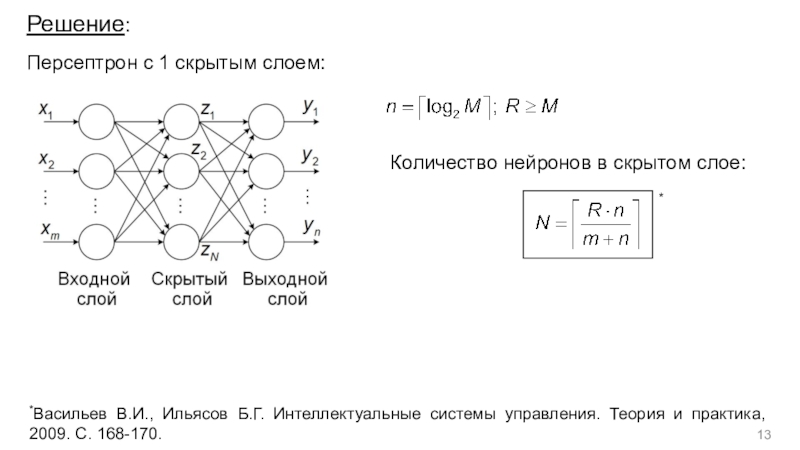
13. Решение:Персептрон с 1 скрытым слоем:Количество нейронов в
14. ПРИМЕРДано: 7х5 матрица входных образов (изображений):M =
15. Скачать презентанцию

в противном случае.1943 – формальный нейрон (МакКаллок, Питтс):если ;в противном случае.1958 – расширение модели (МакКаллок):если ;Здесь: «тормозящие» входы; «возбуждающие» входы

Главная
Разное
Лекция 5 Обобщенная модель нейрона. Персептрон (структура, алгоритмы

Слайды и текст этой презентации

Слайд 1Лекция 5

Обобщенная модель нейрона.
Персептрон (структура, алгоритмы обучения).
Решение задачи распознавания образов

с помощью НС.

Лекция 5Обобщенная модель нейрона.Персептрон (структура, алгоритмы обучения).Решение задачи распознавания образов с помощью НС.

Слайд 2в противном случае.
1943 – формальный нейрон (МакКаллок, Питтс):

если ;

в

противном случае.
1958 – расширение модели (МакКаллок):

если ;

Здесь:

«тормозящие» входы; «возбуждающие» входы

условие возбуждения

( – порог возбуждения)

в противном случае.1943 – формальный нейрон (МакКаллок, Питтс):если ;в противном случае.1958 – расширение модели (МакКаллок):если

Слайд 3ПРОБЛЕМА ИСКЛЮЧАЮЩЕГО ИЛИ (Exclusive OR, XOR)
→ [М. Мински, С. Пейперт,

1969]
Таблица истинности функции XOR

ПРОБЛЕМА ИСКЛЮЧАЮЩЕГО ИЛИ (Exclusive OR, XOR)→ [М. Мински, С. Пейперт, 1969]Таблица истинности функции XOR

Слайд 4Решение проблемы – 2-хслойная НС:

Таблица истинности:
= !
Условия возбуждения нейронов:

Решение проблемы – 2-хслойная НС:Таблица истинности:= !Условия возбуждения нейронов:

Слайд 5ОБОБЩЕННАЯ МОДЕЛЬ НЕЙРОНА

ОБОБЩЕННАЯ МОДЕЛЬ НЕЙРОНА

Слайд 6ВИДЫ ФУНКЦИИ АКТИВАЦИИ

ВИДЫ ФУНКЦИИ АКТИВАЦИИ

Слайд 7ПЕРСЕПТРОН (структура)
1958 – однослойный персептрон (Ф. Розенблат)
→ (от

англ. Perception – «восприятие»)
1958 – 1-й нейрокомпьютер «Марк-1» (Ф. Розенблат)

Структура

многослойного перспетрона

2 режима работы:
обучение (настройка весов НС);
эксплуатация.

– вектор входов,

– вектор выходов,

…

…

ПЕРСЕПТРОН (структура)1958 – однослойный персептрон (Ф. Розенблат) → (от англ. Perception – «восприятие»)1958 – 1-й нейрокомпьютер

Слайд 8ПЕРСЕПТРОН (процедура обучения)
– вектор эталонов, (желаемых выходов) НС;
– вектор ошибки

обучения НС;
Цель обучения:
где – суммарная
квадратичная ошибка обучения (СКО) НС.
…
…

ПЕРСЕПТРОН (процедура обучения)– вектор эталонов, (желаемых выходов) НС;– вектор ошибки обучения НС;Цель обучения:где – суммарная квадратичная ошибка

Слайд 9ОБУЧАЮЩАЯ ВЫБОРКА
– это набор пар –

соответственно входной вектор и вектор желаемых выходов НС r-м обучающем

примере; R – число обучающих примеров(объем обучающей выборки).

ОБУЧАЮЩАЯ ВЫБОРКА– это набор пар – соответственно входной вектор и вектор желаемых выходов

Слайд 10АЛГОРИТМЫ ОБУЧЕНИЯ ПЕРСЕПТРОНА
СКО:
где n – число выходов НС; R –

объем обучающей выборки.
Градиентный алгоритм обучения:
BP = Back Propagation
QP = Quick

Prop
LM = Levenberg- Marquardt

Критерий останова: а) k = Kзад; б) E = Eзад

АЛГОРИТМЫ ОБУЧЕНИЯ ПЕРСЕПТРОНАСКО:где n – число выходов НС; R – объем обучающей выборки.Градиентный алгоритм обучения:BP = Back

Слайд 11СЛОЖНОСТИ ПРОЦЕССА ОБУЧЕНИЯ
«зависание» в локальных минимумах
метод «тяжелого» шарика:

где

регуляризация процесса обучения:

где

– коэффициент «штрафа» весов НС;
эффект «переобучения» (over-learning) НС
выбор оптимальной сложности НС (количества нейронов в скрытом слое); тестирование / валидация НС.

СЛОЖНОСТИ ПРОЦЕССА ОБУЧЕНИЯ«зависание» в локальных минимумахметод «тяжелого» шарика: где регуляризация процесса обучения:

Слайд 12РЕШЕНИЕ ЗАДАЧИ РАСПОЗНАВАНИЯ ОБРАЗОВ С ПОМОЩЬЮ ПЕРСЕПТРОНА
Задача классификации (распознавания образов):
требуется

определить, к какому из M известных классов относится предъявляемый объект

(образ), представленный вектором

Множество входных векторов (признаков)

Множество решений (классов принадлежности)

РЕШЕНИЕ ЗАДАЧИ РАСПОЗНАВАНИЯ ОБРАЗОВ С ПОМОЩЬЮ ПЕРСЕПТРОНАЗадача классификации (распознавания образов):требуется определить, к какому из M известных классов

Слайд 13Решение:

Персептрон с 1 скрытым слоем:
Количество нейронов в скрытом слое:

*
*Васильев В.И.,

Ильясов Б.Г. Интеллектуальные системы управления. Теория и практика, 2009. С.

168-170.

Решение:Персептрон с 1 скрытым слоем:Количество нейронов в скрытом слое:**Васильев В.И., Ильясов Б.Г. Интеллектуальные системы управления. Теория и

Слайд 14ПРИМЕР
Дано: 7х5 матрица входных образов (изображений):
M = 64 (буквы, цифры,

символы); входы
вектор желаемых реакций НС: – двоичный

код / номер образа (класса изображений).

Решение:

Структура НС: 35 – 10 – 6:

Количество настраиваемых параметров (весов) НС:

– матрицы

весов синаптических связей;

– сигмоидные функции

активации

ПРИМЕРДано: 7х5 матрица входных образов (изображений):M = 64 (буквы, цифры, символы); входы вектор желаемых реакций НС:

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей