Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 7. Аксонометрические проекции
Содержание
- 1. Лекция 7. Аксонометрические проекции
- 2. 1. Аксонометрические изображенияех/e = kxеy/e = kyеz/е
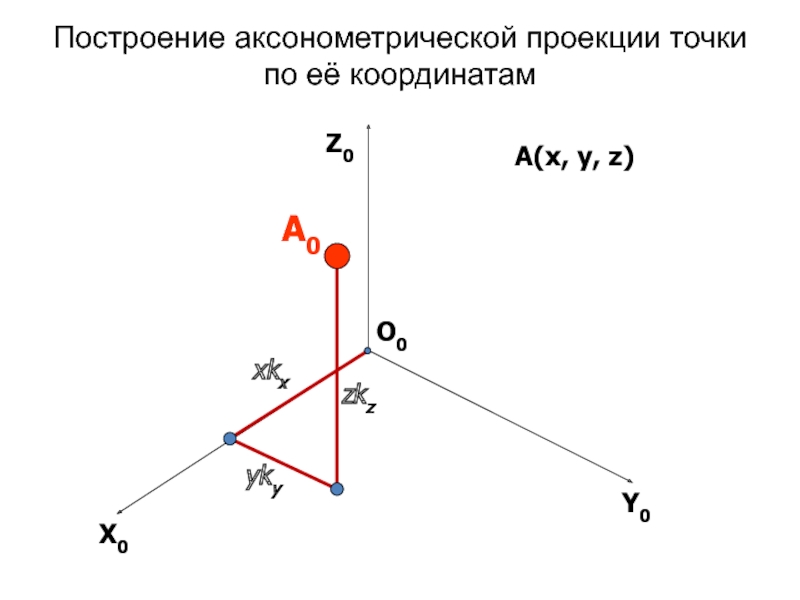
- 3. Построение аксонометрической проекции точки по её координатамxkxykyzkzX0Y0Z0А0О0А(x, y, z)
- 4. 2. Теорема ПолькеТри отрезка произвольной длины, лежащие
- 5. 3. Классификация аксонометрических проекций1. По направлению проецирующих
- 6. 4. Прямоугольные изометрия и диметрияКоэффициенты искаженияИзометрияkx =
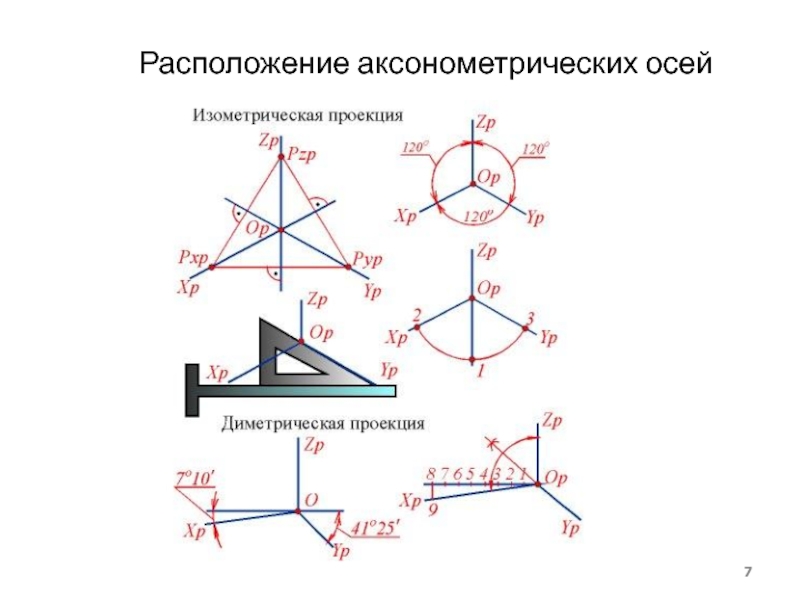
- 7. Расположение аксонометрических осей
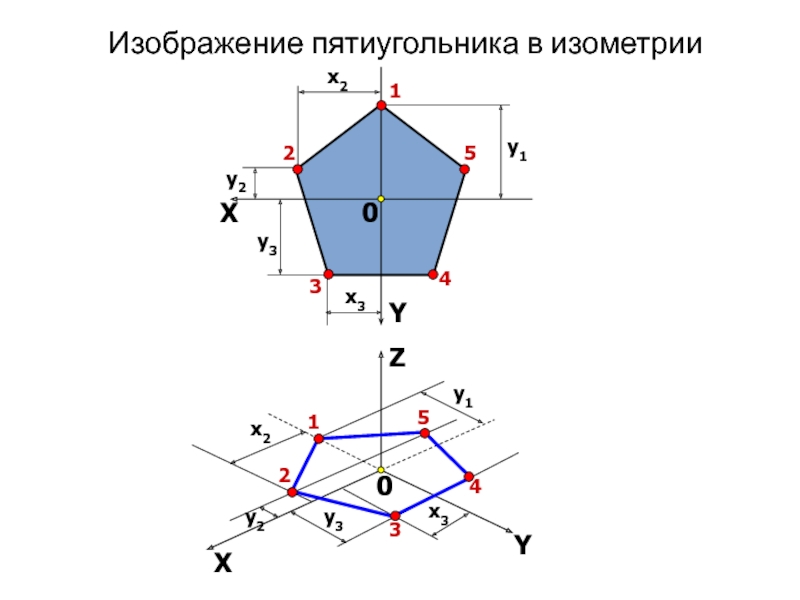
- 8. ХYXYZ12345y11y1x2y2x2y22x3y3x3y334500Изображение пятиугольника в изометрии
- 9. Z0XYyx3x2ZXYx2y0Зеркально отразим точку 3относительно оси OX123456321Так как
- 10. Изображение окружности в аксонометрииПрямоугольная изометрияАВСDYZXAB = 1,22d
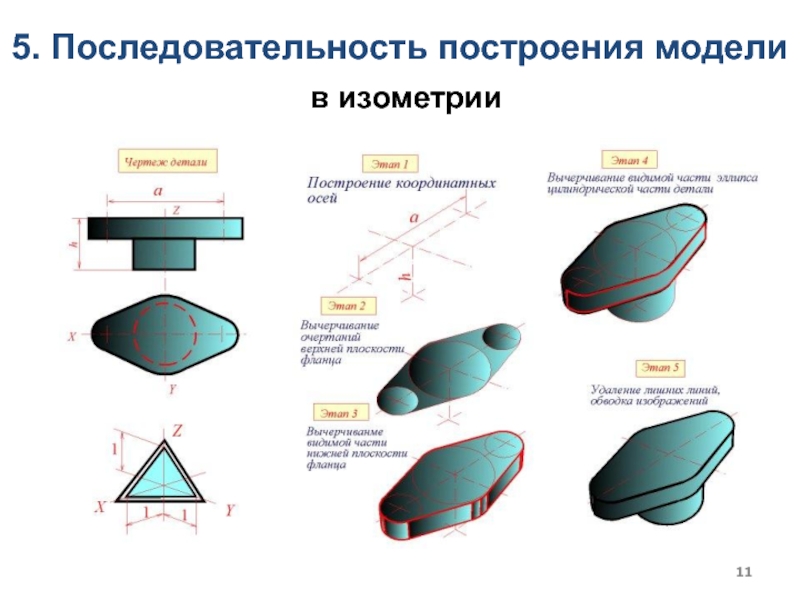
- 11. 5. Последовательность построения моделив изометрии
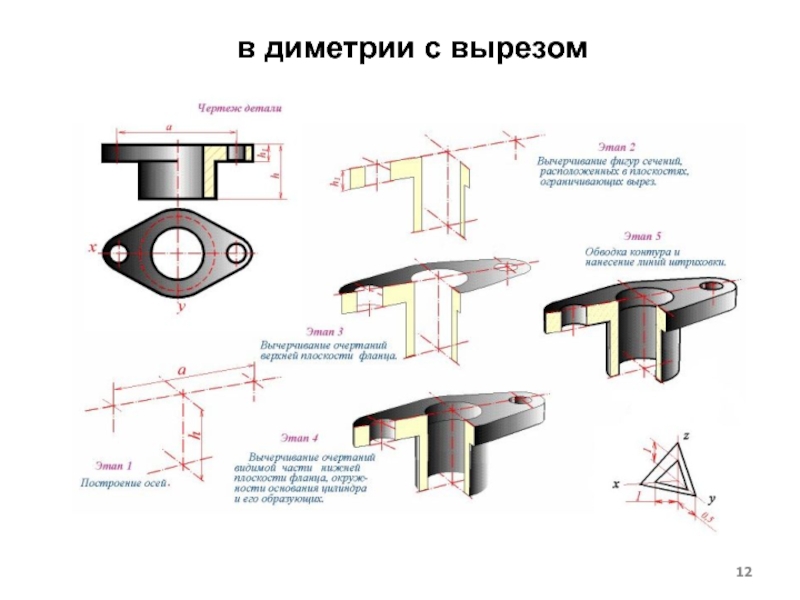
- 12. в диметрии с вырезом
- 13. Спасибо за внимание!
- 14. Построение развёрток геометрических фигурПреобразование поверхности геометрической фигуры,
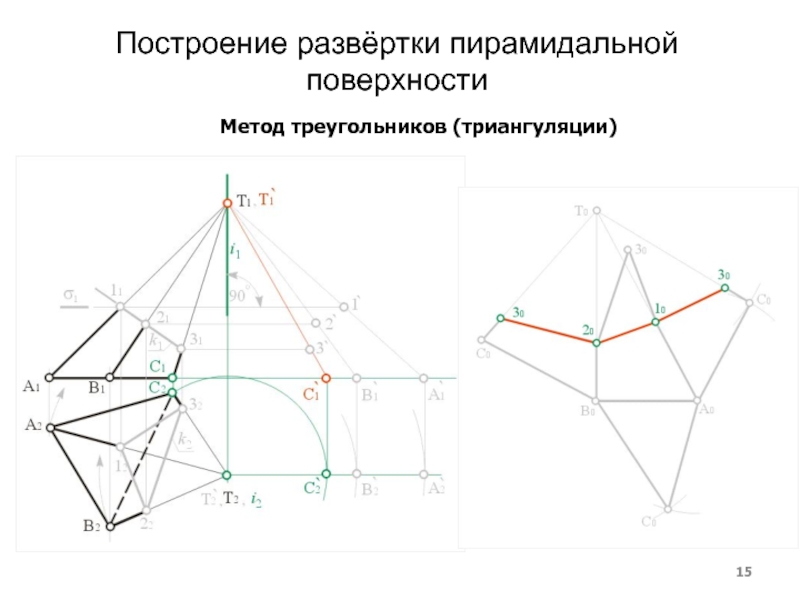
- 15. Построение развёртки пирамидальной поверхностиМетод треугольников (триангуляции)
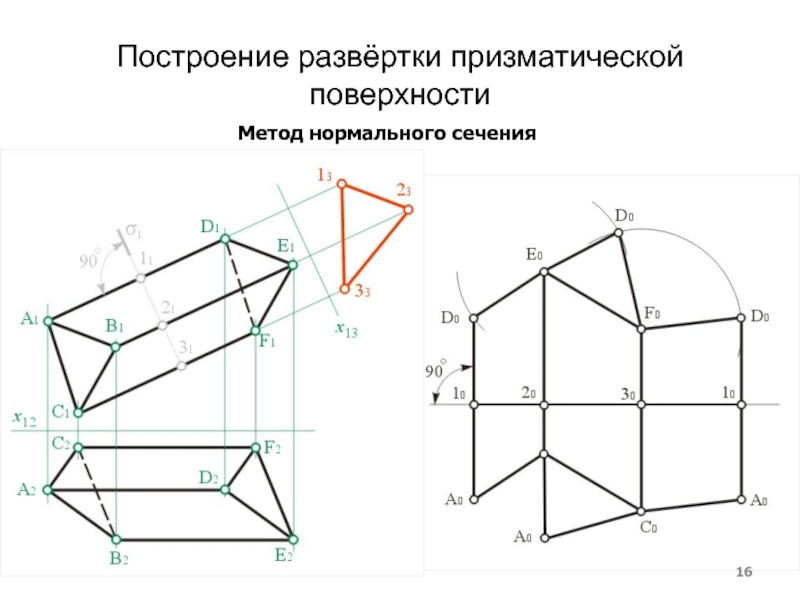
- 16. Построение развёртки призматической поверхностиМетод нормального сечения
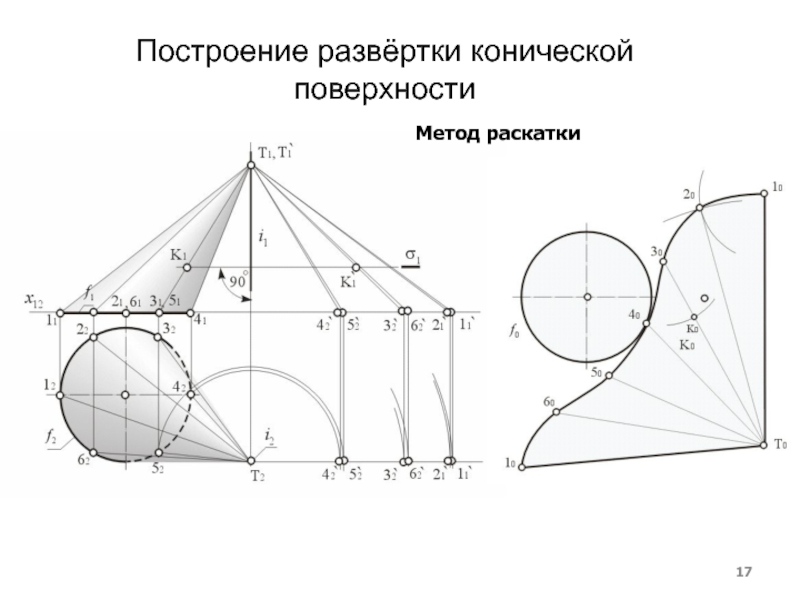
- 17. Построение развёртки конической поверхностиМетод раскатки
- 18. Желаю здравствовать!
- 19. Скачать презентанцию
1. Аксонометрические изображенияех/e = kxеy/e = kyеz/е = kz Коэффициенты искажения:е – натуральный масштабех , еy , еz – аксонометрические масштабы по осямOоAх*Axy*Aо – аксонометрическая координатная ломанаяAо – аксонометрическая проекция точки
Слайды и текст этой презентации
Слайд 1Лекция 7.
Аксонометрические проекции
Аксонометрические изображения.
Теорема Польке.
Классификация
аксонометрических проекций.
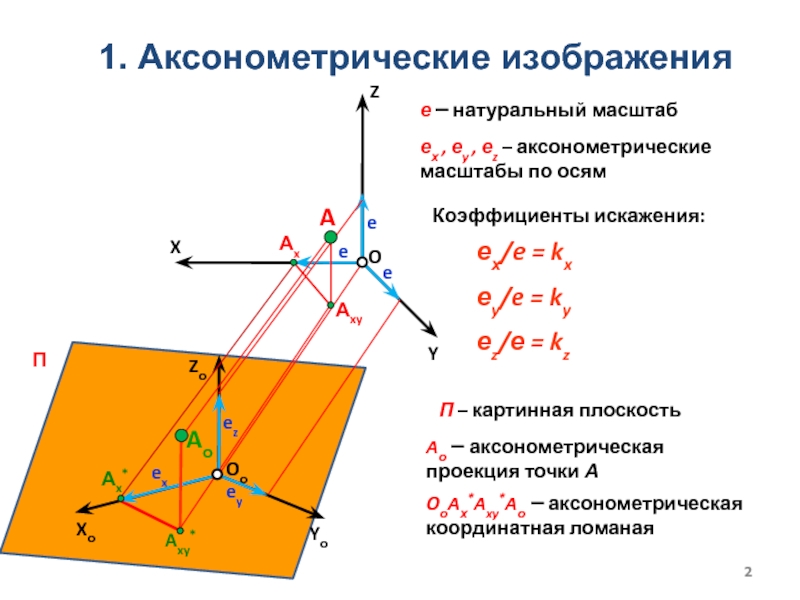
Слайд 21. Аксонометрические изображения
ех/e = kx
еy/e = ky
еz/е = kz
Коэффициенты
искажения:
е – натуральный масштаб
ех , еy , еz – аксонометрические
масштабы по осямOоAх*Axy*Aо – аксонометрическая координатная ломаная
Aо – аксонометрическая проекция точки А
Z
Y
Xо
Zо
X
Yо
e
e
e
A
Аxy
Oо
ex
ez
ey
Аx
Аx*
Axy*
Aо
П
O
П – картинная плоскость
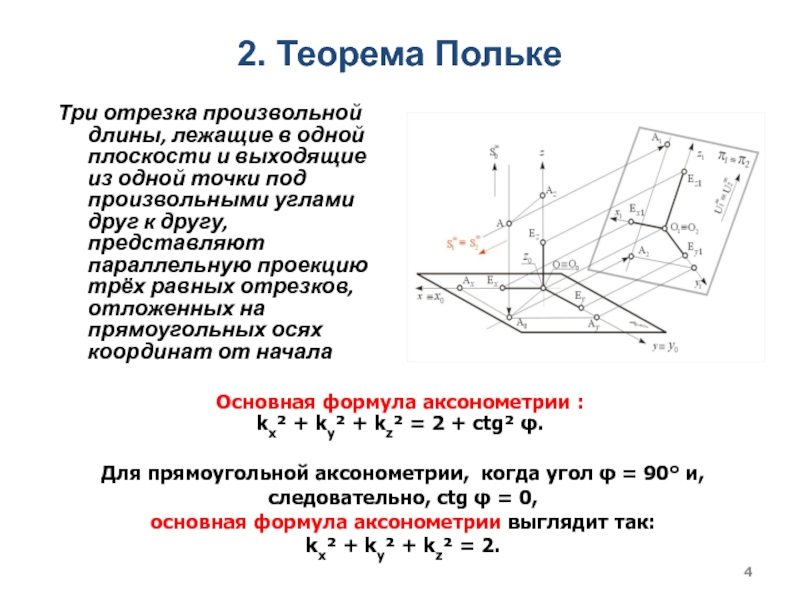
Слайд 42. Теорема Польке
Три отрезка произвольной длины, лежащие в одной плоскости
и выходящие из одной точки под произвольными углами друг к
другу, представляют параллельную проекцию трёх равных отрезков, отложенных на прямоугольных осях координат от начала
Основная формула аксонометрии :
kx² + ky² + kz² = 2 + ctg² φ.
Для прямоугольной аксонометрии, когда угол φ = 90° и, следовательно, ctg φ = 0,
основная формула аксонометрии выглядит так:
kx² + ky² + kz² = 2.
Слайд 53. Классификация аксонометрических проекций
1. По направлению проецирующих лучей
косоугольные (при произвольном
направлении проецирующих лучей)
прямоугольные (при направлении проецирования, перпендикулярном к плоскости
проекций)2. По коэффициентам искажения
изометрическая, когда коэффициенты искажения по всем трём осям одинаковы (kx = ky = kz)
диметрическая, когда коэффициенты искажения одинаковы только по двум осям (kx = ky kz или
kx = kz ky, или kz = ky kx)
триметрическая, когда коэффициенты искажения по всем трём осям различны (kx ky kz)
Слайд 64. Прямоугольные изометрия и диметрия
Коэффициенты искажения
Изометрия
kx = ky = kz
Из
основной формулы аксонометрии:
kx = ky = kz ≈ 0,82. Считаем,
что kx = ky = kz = 1Диметрия
kx = kz, ky = 0,5kx
Из основной формулы аксонометрии:
kx = kz ≈ 0,94. ky ≈ 0,47. Считаем, что kx = kz = 1, ky = 0,5
Слайд 9Z
0
X
Y
y
x3
x2
Z
X
Y
x2
y
0
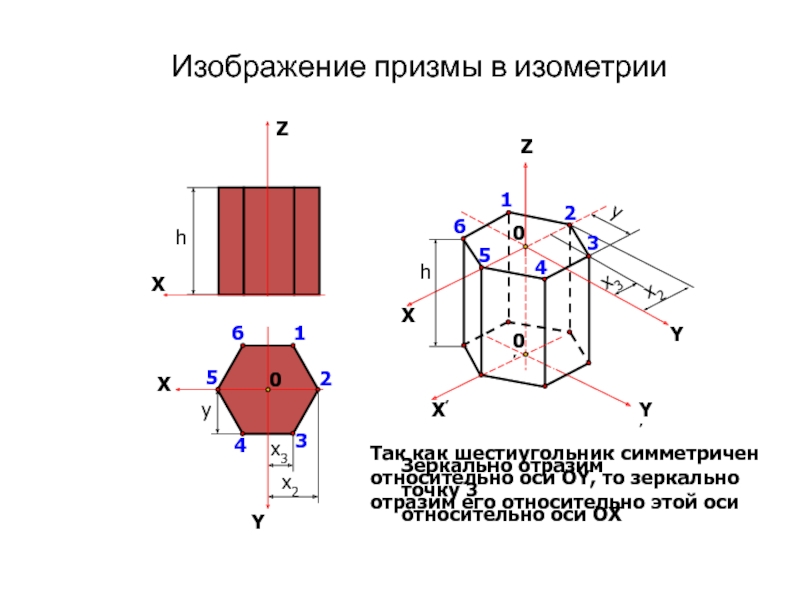
Зеркально отразим точку 3
относительно оси OX
1
2
3
4
5
6
3
2
1
Так как шестиугольник симметричен
относительно оси
OY, то зеркально
отразим его относительно этой оси
x3
4
5
6
X’
Y’
0’
X
Изображение призмы в
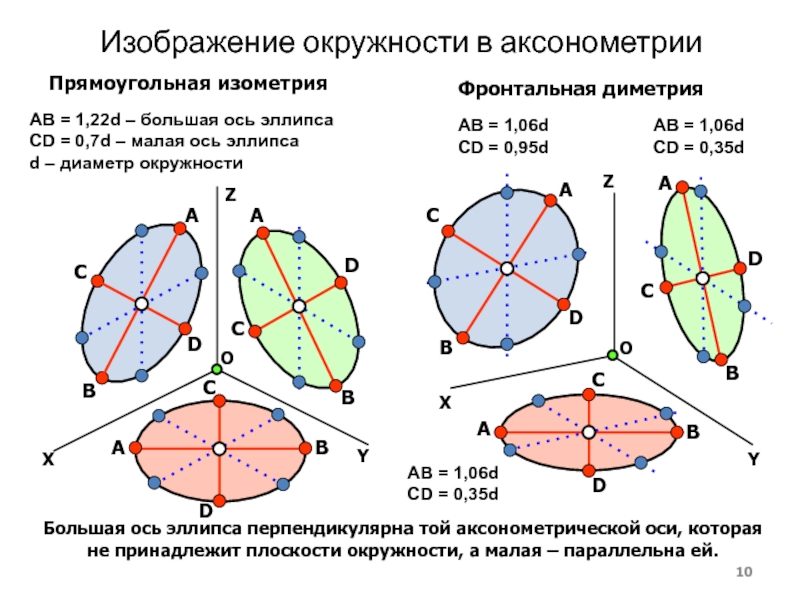
изометрии
Слайд 10Изображение окружности в аксонометрии
Прямоугольная изометрия
А
В
С
D
Y
Z
X
AB = 1,22d – большая ось
эллипса CD = 0,7d – малая ось эллипса
d – диаметр окружностиО
AB = 1,06d CD = 0,95d
AB = 1,06d CD = 0,35d
AB = 1,06d CD = 0,35d
Фронтальная диметрия
Большая ось эллипса перпендикулярна той аксонометрической оси, которая не принадлежит плоскости окружности, а малая – параллельна ей.
А
В
С
D
А
В
С
D
А
В
С
D
А
В
С
D
А
В
С
D
Y
Z
X
О
Слайд 14Построение развёрток геометрических фигур
Преобразование поверхности геометрической фигуры, при котором поверхность
совмещается с некоторой плоскостью 0 без складок и разрывов, называется
построением развёртки заданной поверхности. Поверхности, допускающие такое преобразование, называются развертывающимися, а фигура, совмещённая с плоскостью 0, в которую преобразуется поверхность, называется развёрткой поверхности.
