Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 7. Помехи в каналах связи
Содержание
- 1. Лекция 7. Помехи в каналах связи
- 2. 1. Основные понятия каналов связи.В любой системе
- 3. Каналы связи классифицируют по различным признакам:по назначению;по
- 4. Возможна также классификация каналов поназначению: телеграфные, телефонные,
- 5. Слайд 5
- 6. 2. Модели каналов связи.Модели непрерывных каналов.Непрерывными называются
- 7. Непрерывные каналы можно классифицировать по виду помех
- 8. При передаче сигнала S(t) на него действуют
- 9. График плотности вероятности W(x) представляет собой колоколообразную кривую
- 10. Выходной сигнал гауссовского каналаU(t) = S(t) +
- 11. Гауссовский канал с неизвестной фазой сигнала определяется
- 12. Модели дискретных каналов.Дискретными называются каналы, входные и
- 13. Классификацию дискретных каналов удобно вести по вектору
- 14. Вероятности P(0/0) и P(1/1) характеризуют правильный прием
- 15. Марковский канал является простейшей моделью дискретного канала
- 16. Каноническая схема системы связи на основе дискретного (цифрового)
- 17. 3. Помехи в каналах.Информация в канале связи
- 18. Видно, что помеха искажает и частоту сигнала
- 19. Если отношение сигнал/помеха увеличить каким-либо образом до
- 20. Слайд 20
- 21. Реальная смесь сигнала и помехи в радиоканале
- 22. Детерминированные изменения сигнала определяются структурой канала и
- 23. Под помехой (шумом) будем понимать всякое случайное
- 24. Внешние шумы проявляются в виде аддитивных и
- 25. Помеха, сосредоточенная по частоте имеет спектр значительно
- 26. Помехи как случайный процесс.Математическая модель изменяющегося во
- 27.
- 28.
- 29. Корреляционная функция.Характеристикой динамики изменения двумерной случайной величины
- 30.
- 31. Скачать презентанцию
Слайды и текст этой презентации
Слайд 21. Основные понятия каналов связи.
В любой системе электросвязи должны быть
устройства, осуществляющие преобразования: на передаче – информация → сообщение →
сигнал, на приеме – сигнал → сообщение → информация. Кроме того, в процессе передачи сигнал подвергается и другим преобразованиям, многие из которых являются типовыми, обязательными для различных систем электросвязи, независимо от их назначения и характера передаваемых сообщений.Схема типового канала связи, предназначенного для передачи сообщений от источника к получателю. Часть канала от источника сообщения до среды распространения (линии связи) называется передатчиком, а от среды распространения до получателя сообщения – приёмником.
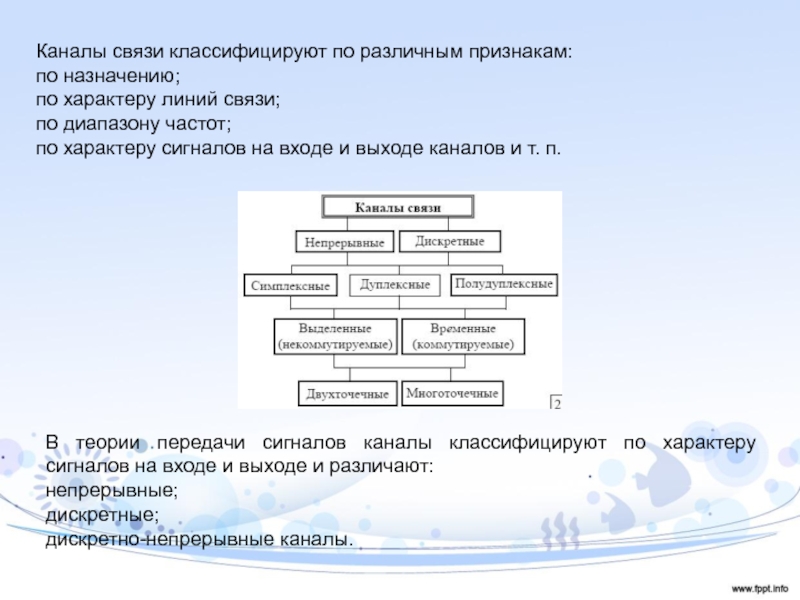
Слайд 3Каналы связи классифицируют по различным признакам:
по назначению;
по характеру линий связи;
по
диапазону частот;
по характеру сигналов на входе и выходе каналов и
т. п.В теории передачи сигналов каналы классифицируют по характеру сигналов на входе и выходе и различают:
непрерывные;
дискретные;
дискретно-непрерывные каналы.
Слайд 4Возможна также классификация каналов по
назначению: телеграфные, телефонные, телевизионные, телеметрические и
др.;
виду физической среды распространения: проводные, кабельные, волноводные и др.;
и
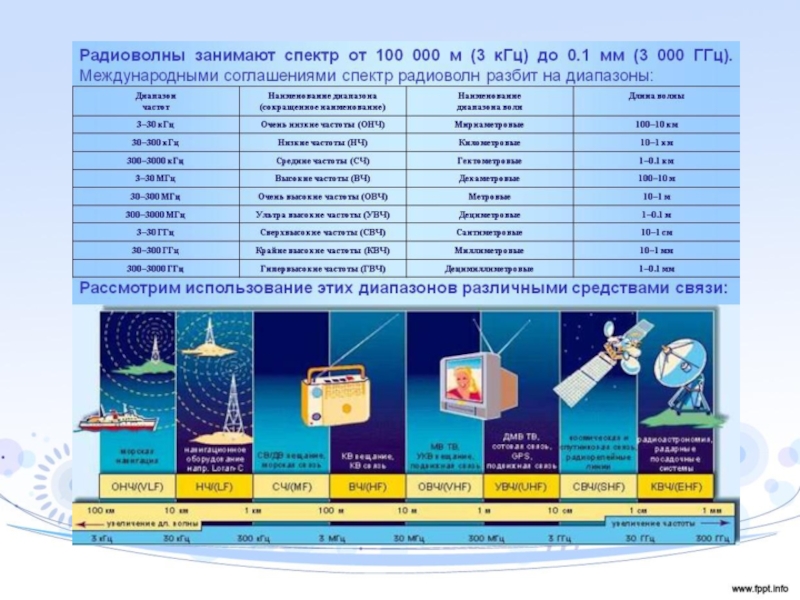
диапазону используемых ими частот.К радиодиапазону относят частоты в пределах 30 ... 30·1012 Гц, что соответствует длинам волн от 108 м до 0,1 мм.
Кроме радиодиапазона, в настоящее время широкое распространение нашел и оптический диапазон волн.
По способу распространения радиоволн различают каналы: с открытым и с закрытым распространением.
В каналах с закрытым распространением электромагнитная энергия распространяется по направляющим линиям (кабельные, проводные, волноводные СВЧ тракты и др.): для них характерны малый уровень помех и постоянство параметров сигнала, что позволяет передавать информацию с высокой скоростью и достоверностью.
Слайд 62. Модели каналов связи.
Модели непрерывных каналов.
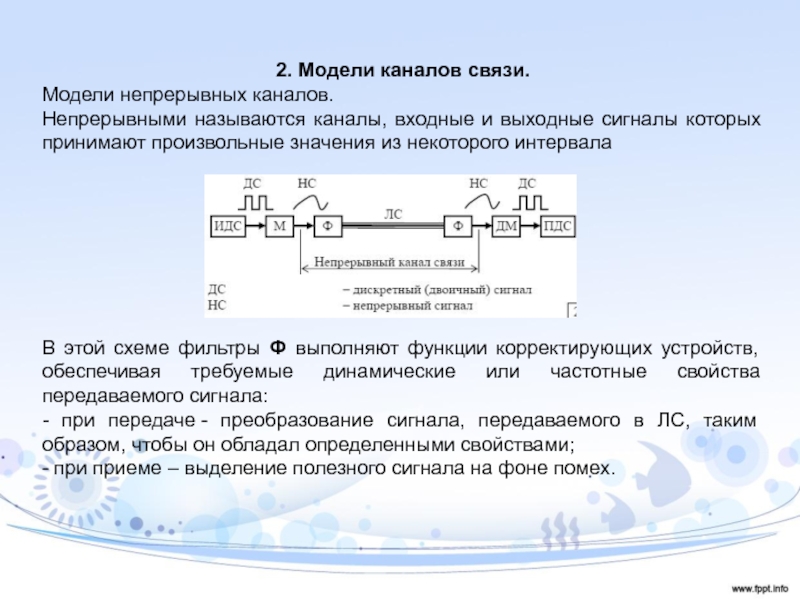
Непрерывными называются каналы, входные и
выходные сигналы которых принимают произвольные значения из некоторого интервала
В
этой схеме фильтры Ф выполняют функции корректирующих устройств, обеспечивая требуемые динамические или частотные свойства передаваемого сигнала:- при передаче - преобразование сигнала, передаваемого в ЛС, таким образом, чтобы он обладал определенными свойствами;
- при приеме – выделение полезного сигнала на фоне помех.
Слайд 7Непрерывные каналы можно классифицировать по виду помех и характеру преобразования
S(t) на выходе передатчика в полезный принятый U(t) на входе
приёмника. Если ограничиться предположением, что в канале действует аддитивный нормальный белый шум n(t), то непрерывные каналы подразделяются по виду преобразования S(t) в U(t), т.е. по виду искажений сигнала. До недавнего времени в большинстве радиотехнических систем излученные сигналы являлись узкополосными.Узкополосный сигнал – это сигнал, эффективная ширина спектра которого ∆ωэф значительно меньше центральной частоты ω0 , вокруг которой группируются спектральные составляющие сигнала. Физически такой сигнал относится к квазигармоническим сигналам, общее выражение для которых имеет вид
S(t) = A(t) cos[ω0t + φ(t)],
где A(t) и φ(t) – функции, отображающие законы амплитудной и угловой модуляции; ω0 – несущая частота сигнала. Радиосигналы, ширина спектра которых сравнима с центральной частотой, относят к широкополосным.
Иногда используется коэффициент 1/10, т.е. если ширина спектра составляет около 1/10 от частоты, на которой передается сигнал, то сигнал считается широкополосным. При более узком спектре сигнал будет узкополосным, при более широком - сверхширокополосным.
Слайд 8При передаче сигнала S(t) на него действуют помехи n(t), которые
в большинстве случаев являются аддитивными, т.е. суммирующимися с сигналом S(t),
превращая его в сигнал U(t)U(t) = S(t) + n(t).
Гауссовским каналом называется канал, в котором действует аддитивный нормальный белый шум n(t), а искажения полезного сигнала несущественны и могут быть скомпенсированы.
Поскольку шум образуется как сумма большого числа отдельных независимых колебаний, он, согласно центральной предельной теореме представляет собой стационарный эргодический случайный процесс с гауссовским (нормальным) распределением вероятности. Иначе этот шум называется «белым» шумом, для которого характерно наличие составляющих всех частот от 0 до ∞.
Плотность распределения вероятностей (ПРВ) гауссовского процесса описывается формулой
,
в которую входят два числовых параметра m и σ2 , имеющие смысл математического ожидания и дисперсии: m = M(x), σ2 = D(X).
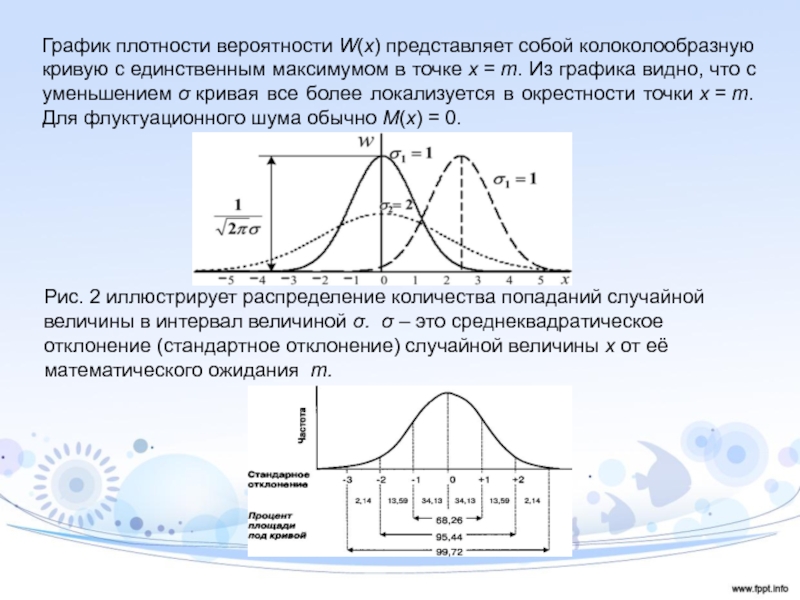
Слайд 9График плотности вероятности W(x) представляет собой колоколообразную кривую с единственным максимумом
в точке x = m. Из графика видно, что с уменьшением σ кривая все более
локализуется в окрестности точки x = m. Для флуктуационного шума обычно M(x) = 0.Рис. 2 иллюстрирует распределение количества попаданий случайной величины в интервал величиной σ. σ – это среднеквадратическое отклонение (стандартное отклонение) случайной величины x от её математического ожидания m.
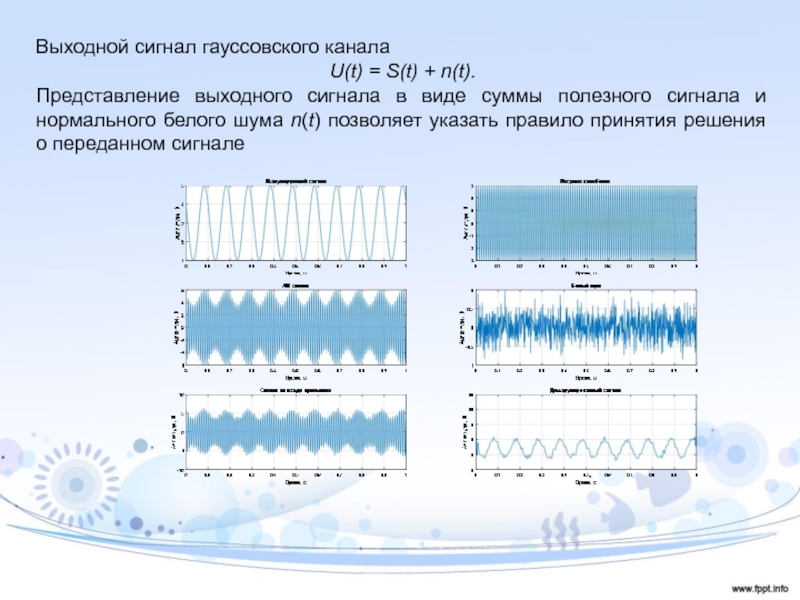
Слайд 10Выходной сигнал гауссовского канала
U(t) = S(t) + n(t).
Представление выходного сигнала
в виде суммы полезного сигнала и нормального белого шума n(t)
позволяет указать правило принятия решения о переданном сигналеСлайд 11Гауссовский канал с неизвестной фазой сигнала определяется параметрами τз, Ω,
α(t) = α, которые постоянны и известны. Фаза θ считается
равномерно распределенной величиной в интервале 0 ÷ 2π. Такая модель хорошо описывает процессы в линиях радиосвязи на расстояниях прямой видимости.Канал с амплитудными замираниями является дальнейшим усложнением канала с неизвестной фазой в предположении, что α(t) – случайная функция времени. Выходной полезный сигнал канала с замираниями
Sp(t,λ) = α(t) A(t) cos[(ω0 + Ω)t + φ(t) - θ].
Случайная функция α(t) перемножается с сигналом и поэтому называется мультипликативной помехой, которую можно рассматривать как функцию, модулирующую по амплитуде излученный сигнал. Модуляция приводит к расширению спектра принятого сигнала относительно спектра излученного сигнала. Поэтому такой канал называют каналом с рассеянием энергии по частоте.
Непрерывный канал считается заданным, если указаны мощность сигналов, полоса частот, дано описание моделей помех и искажений сигналов.
Слайд 12Модели дискретных каналов.
Дискретными называются каналы, входные и выходные сигналы которых
принимают конечное число мгновенных значений. Понятие дискретного канала естественно возникает
при передаче дискретных сообщений и определяется как совокупность технических средств, включенных между кодером и декодером канала.Переход от дискретных сигналов к непрерывным осуществляется на передающей стороне при манипуляции параметрами непрерывной несущей. На приемной стороне дискретные сигналы появляются на выходе первой решающей схемы (демодулятора).
Дискретный канал задается множеством входных {si}, I = 1, Ls и выходных {yj}, j = 1, Ly символов (сигналов), длительностью символов τ и условными вероятностями P(yj/si) преобразования входных символов в выходные. Обычно длительности всех входных и выходных символов одинаковы. Объемы алфавитов входных Ls и выходных Ly сигналов в общем случае могут быть разными, причем Ly ≥ Ls. Однако в большинстве случаев Ly = Ls. Для дискретных каналов широко используется представление принятой последовательности символов Y = (y1, y2,..., yn) в виде суммы переданной последовательности S = (s1, s2,..., sn) и комбинации помехи (вектора ошибки) E = (e1, e2,..., en)
Слайд 13Классификацию дискретных каналов удобно вести по вектору ошибки Е. Разные
модели каналов различаются распределением вероятностей вектора Е. Наиболее распространены следующие
модели.Канал без памяти – это канал, в котором символы ei являются независимыми случайными величинами (СВ). Прием каждого сигнального символа в таком канале не зависит от результата приема предыдущих символов. При наличии такой зависимости имеет место канал с памятью. Дискретный канал называется стационарным, если вероятность ошибочного приема символов не изменяется с течением времени.
В силу простоты технической реализации наибольшее применение находят каналы, сигналы в которых представляются двоичным кодом. Такие каналы называются двоичными (бинарными) и задаются с помощью графа
Слайд 14Вероятности P(0/0) и P(1/1) характеризуют правильный прием символов 0 и
1 соответственно, a P(1/0) и P(0/1) – вероятности ошибок при
приеме символов 0 и 1.Симметричным двоичным называется канал, в котором вероятности ошибок при приеме 0 и 1 одинаковы, P(1/0) = P(0/1), а следовательно, равны и вероятности правильного приема символов P(0/0) = P(1/1) = 1 - p. Для симметричного стационарного канала без памяти вероятность искажения i-го символа P(ei = 1) = p, а вероятность правильного приема P(ei = 0) = 1 – p.
Двоичный канал без памяти со стиранием отличается от рассмотренного тем, что выходной алфавит помимо 0 и 1 содержит третий символ «?» – символ стирания. Он появляется в тех случаях, когда демодулятор не может надежно опознать переданный символ. Такой канал часто используется в системах передачи информации с обратной связью, когда при приеме символа «?» производится повторение передачи. Это позволяет значительно снизить вероятность ошибочного приема за счет уменьшения скорости передачи.
Слайд 15Марковский канал является простейшей моделью дискретного канала с памятью. Он
характеризуется вектором ошибки, символы которого образуют простую цепь Маркова. Вероятность
искажения символа в этом канале зависит от результата приема только предыдущего символа.Марковская модель задается матрицей переходных вероятностей:
где p1 – условная вероятность принять (i + 1)-й символ ошибочно, если i-й принят правильно; 1- p1 – условная вероятность принять (i + 1)-й символ правильно, если i-й принят правильно; p2 – условная вероятность принять (i + 1)-й символ ошибочно, если i-й принят ошибочно; 1- p2 – условная вероятность принять (i + 1)-й символ правильно, если i-й принят ошибочно.
Безусловная (средняя) вероятность ошибки в рассматриваемом канале должна удовлетворять уравнению:
p(xi+1 / xi) = p2 ∙ pош(xi) + p1 ∙ pправ(xi)
или
p(xi+1 / xi) = p1 / (1 + p1 + p2).
Слайд 16Каноническая схема системы связи на основе дискретного (цифрового) канала связи содержит:
- устройство
сопряжения с каналом связи (УС);
- устройство защиты от ошибок (УЗО);
-
устройство преобразования сигналов (УПС).Слайд 173. Помехи в каналах.
Информация в канале связи передаётся различными электрическими
и оптическими сигналами, на которые воздействуют различные помехи, приводящие к
искажениям сигналов и, следовательно, к искажению передаваемой информации. Поэтому основная задача при передаче информации состоит в том, чтобы организовать канал с минимальными потерями. Для этого, естественно, надо применять такие методы обработки сигналов, которые позволили бы свести воздействие помех к минимуму.Для примера рассмотрим частотно-манипулированыый сигнал на который воздействует аддитивная помеха в виде нормального «белого» шума различной интенсивности
Слайд 18Видно, что помеха искажает и частоту сигнала и его амплитуду.
В данном случае отношение сигнал/помеха имеет минимально приемлемое значение 3:1.
Слайд 19Если отношение сигнал/помеха увеличить каким-либо образом до нормальной величины 10:1,
то влияние помехи и на амплитуду сигнала и на его
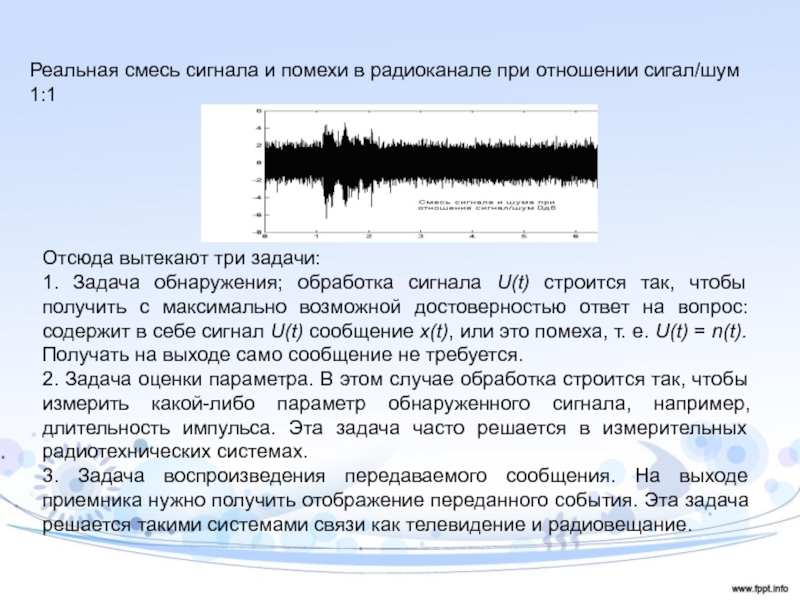
частоту будет минимальнымСлайд 21Реальная смесь сигнала и помехи в радиоканале при отношении сигал/шум
1:1
Отсюда вытекают три задачи:
1. Задача обнаружения; обработка сигнала U(t)
строится так, чтобы получить с максимально возможной достоверностью ответ на вопрос: содержит в себе сигнал U(t) сообщение x(t), или это помеха, т. е. U(t) = n(t). Получать на выходе само сообщение не требуется.2. Задача оценки параметра. В этом случае обработка строится так, чтобы измерить какой-либо параметр обнаруженного сигнала, например, длительность импульса. Эта задача часто решается в измерительных радиотехнических системах.
3. Задача воспроизведения передаваемого сообщения. На выходе приемника нужно получить отображение переданного события. Эта задача решается такими системами связи как телевидение и радиовещание.
Слайд 22Детерминированные изменения сигнала определяются структурой канала и заключаются в определенном
изменении масштаба сигнала (усиление или затухание), смещении во времени (задержка)
и изменении формы (искажения).Случайные изменения сигнала определяются помехой, действующей в канале, и заключаются в случайном изменении тех же показателей — масштаба, задержки, искажений.
Слайд 23Под помехой (шумом) будем понимать всякое случайное воздействие на сигнал
в канале связи, препятствующее правильному приёму сигналов.
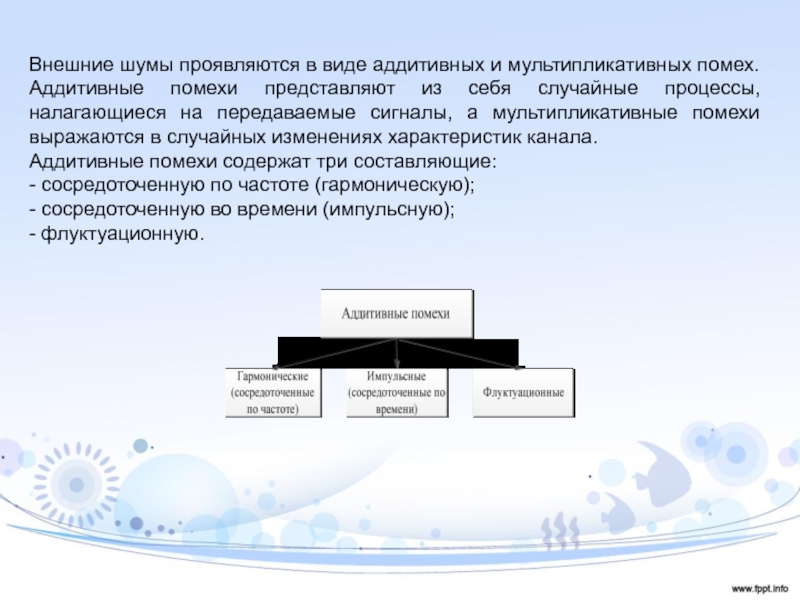
Слайд 24Внешние шумы проявляются в виде аддитивных и мультипликативных помех. Аддитивные
помехи представляют из себя случайные процессы, налагающиеся на передаваемые сигналы,
а мультипликативные помехи выражаются в случайных изменениях характеристик канала.Аддитивные помехи содержат три составляющие:
- сосредоточенную по частоте (гармоническую);
- сосредоточенную во времени (импульсную);
- флуктуационную.
Слайд 25Помеха, сосредоточенная по частоте имеет спектр значительно уже полосы пропускания
канала (но по отношению к ширине спектра сигнала она может
быть узкополосной или широкополосной).Импульсная помеха представляет собой последовательность кратковременных импульсов, разделенных интервалами, превышающими время переходных процессов в канале.
Флуктуационную помеху можно представить как последовательность непрерывно следующих один за другим импульсов, имеющую широкий спектр, выходящий за пределы полосы пропускания канала.
Импульсную помеху можно рассматривать как крайний случай флуктуационной, когда её энергия сосредоточена в отдельных точках временной оси, а гармоническую помеху — как другой крайний случай, когда вся энергия сосредоточена в отдельных точках частотной оси.
Слайд 26Помехи как случайный процесс.
Математическая модель изменяющегося во времени случайного сигнала
называется случайным процессом.
Случайный процесс Х(t) представляет собой функцию, которая
отличается тем, что принимаемые ею значения в любые произвольные моменты времени по координате t являются случайными. Случайный процесс X(t) следует рассматривать как совокупность временных функций xk(t), называемых реализациями, имеющих определенную общую статистическую закономерность. Слайд 29Корреляционная функция.
Характеристикой динамики изменения двумерной случайной величины {X(ti), X(tj)} является
корреляционная функция, которая описывает случайный процесс в целом:
RX(ti,tj) = M{X(t1)
X(t2)}.Корреляционная функция служит для описания скорости изменения случайного процесса во времени и представляет собой статистически усредненное произведение значений случайного процесса X(t) в моменты времени ti и tj по всем значениям временных осей ti и tj, а следовательно тоже является двумерной функцией, но в этом случае она называется автокорреляционной функцией (корреляция с самой собой, но сдвинутой во времени)