Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 9
Содержание
- 1. Лекция 9
- 2. Принцип гюйгенса-френеляДифракцией любое отклонение распространения волн вблизи
- 3. Если точка наблюдения расположена достаточно далеко от
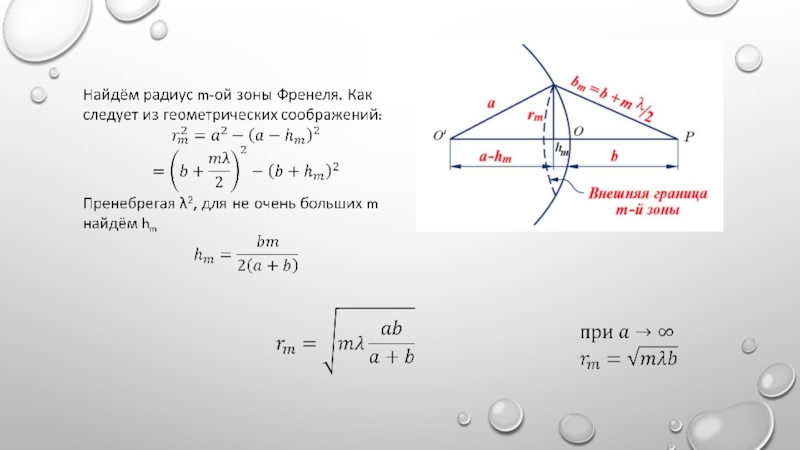
- 4. Элементарное колебание можно изобразить на векторной диаграмме
- 5. Слайд 5
- 6. Приближение коротких длин волн Число Френеля
- 7. Дифракция фраунгофера на щели
- 8. Слайд 8
- 9. Главному максимуму соответствует освещённая область, а побочным
- 10. Дифракционный предел разрешения оптических инструментов
- 11. Скачать презентанцию
Принцип гюйгенса-френеляДифракцией любое отклонение распространения волн вблизи препятствий от законов геометрической оптикиЯвление дифракции объясняется с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а
Слайды и текст этой презентации
Слайд 2Принцип гюйгенса-френеля
Дифракцией любое отклонение распространения волн вблизи препятствий от законов
геометрической оптики
каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени. Т.е. световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн. Обычно в качестве этой поверхности выбирают одну из волновых поверхностей, поэтому все фиктивные источники действуют синфазно. Исключается возможность возникновения обратных вторичных волн.Слайд 3Если точка наблюдения расположена достаточно далеко от препятствия и в
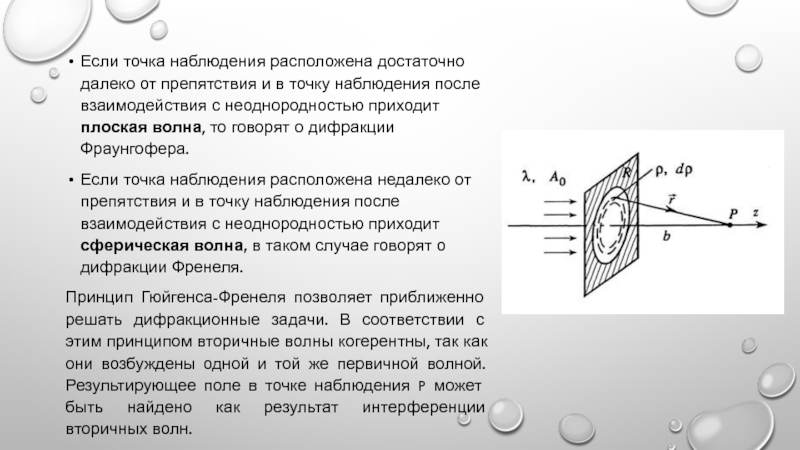
точку наблюдения после взаимодействия с неоднородностью приходит плоская волна, то
говорят о дифракции Фраунгофера.Если точка наблюдения расположена недалеко от препятствия и в точку наблюдения после взаимодействия с неоднородностью приходит сферическая волна, в таком случае говорят о дифракции Френеля.
Принцип Гюйгенса-Френеля позволяет приближенно решать дифракционные задачи. В соответствии с этим принципом вторичные волны когерентны, так как они возбуждены одной и той же первичной волной. Результирующее поле в точке наблюдения P может быть найдено как результат интерференции вторичных волн.
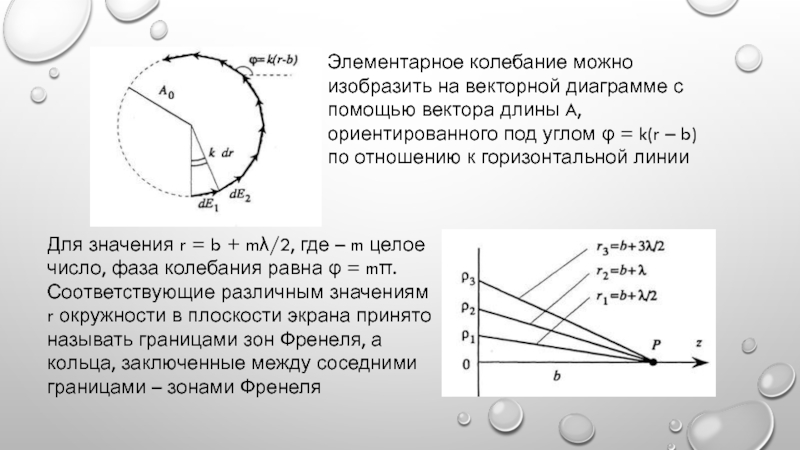
Слайд 4Элементарное колебание можно изобразить на векторной диаграмме с помощью вектора
длины A, ориентированного под углом φ = k(r – b)
по отношению к горизонтальной линииДля значения r = b + mλ/2, где – m целое число, фаза колебания равна φ = mπ. Соответствующие различным значениям r окружности в плоскости экрана принято называть границами зон Френеля, а кольца, заключенные между соседними границами – зонами Френеля
Слайд 9Главному максимуму соответствует освещённая область, а побочным – убывающие по
интенсивности светлые полосы равной ширины, параллельные краям щели. Величина главного
максимума Ic распределения интенсивности дифракционной волны пропорциональна квадрату ширины щели b2.Угловой размер наблюдаемого главного дифракционного максимума Δφm можно оценить по расстоянию между первыми нулями функции I(φ) при смещении из центра картины в зону тени. Это не единственный способ определить угловую ширину наблюдаемого дифракционного пятна. Согласно Рэлею ширина пятна определяется разностью угловых координат, соответствующих уменьшению максимального значения интенсивности в два раза.
Для щелей, освещаемых световыми волнами, практически всегда выполняется условие λ/b << 1. В соответствии с этим условием получаем, что угловой размер наблюдаемой дифракционной полосы Δφm = arcsin(λ/b) ≈ λ/b обратно пропорционален ширине щели, выраженной в длинах волн.