Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 9 Многообразие задач выбора
Содержание
- 1. Лекция 9 Многообразие задач выбора
- 2. Задача выбораВыбор является действием, придающим всей деятельности
- 3. Понятия, общие для всех задач выбора1. Будем
- 4. Множественность задач выбораРазличие математической постановки задач обусловлено
- 5. Критериальный язык – один из основных языков
- 6. Оптимизация по одному «суперкритерию»:
- 7. Условная максимизация: выделение основного критерия и рассмотрение
- 8. Поиск альтернативы с заданными свойствамиxначЦель оптимизации: начиная
- 9. Определение паретовского множества альтернатив- Множество Паретоq10, q20
- 10. Классификация задач выбора и способов их решения
- 11. Примеры постановок задач выбора, отличных от
- 12. Выбор и отбор«Выбор» осуществляется один раз, даже
- 13. Введение в теорию «элитных групп»Из исходного множества
- 14. Техническое выполнение презентации: студент гр. 41-Р Кожин
- 15. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Лекция 9
Многообразие задач выбора
1. Введение
2. Критериальный язык выбора
3. Примеры других
постановок задач выбора
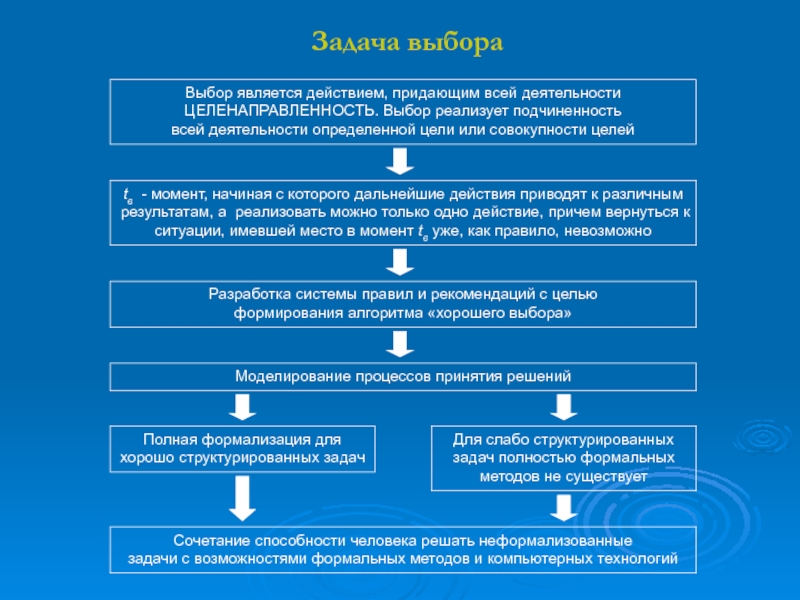
Слайд 2Задача выбора
Выбор является действием, придающим всей деятельности ЦЕЛЕНАПРАВЛЕННОСТЬ. Выбор реализует
подчиненность
всей деятельности определенной цели или совокупности целей
tв - момент,
начиная с которого дальнейшие действия приводят к различным результатам, а реализовать можно только одно действие, причем вернуться к ситуации, имевшей место в момент tв уже, как правило, невозможноРазработка системы правил и рекомендаций с целью
формирования алгоритма «хорошего выбора»
Сочетание способности человека решать неформализованные
задачи с возможностями формальных методов и компьютерных технологий
Моделирование процессов принятия решений
Полная формализация для
хорошо структурированных задач
Для слабо структурированных
задач полностью формальных
методов не существует
Слайд 3Понятия, общие для всех задач выбора
1. Будем представлять принятие решения
ВЫБОРА как действие над множеством альтернатив, в результате которого получается
подмножество выбранных альтернатив2. Сужение множества альтернатив возможно, если существует способ сравнения альтернатив между собой и определение наиболее предпочтительных – КРИТЕРИЙ ПРЕДПОЧТЕНИЯ
Считаются уже пройденными этапы: порождение множества альтернатив, на котором предстоит осуществлять выбор (т.е. существуют некоторые данные об изучаемом явлении или системе, которые представлены в единой форме); определение целей, ради достижения которых производится выбор, сформулирован критерий предпочтения
Слайд 4Множественность задач выбора
Различие математической постановки задач обусловлено тем, что каждая
компонента ситуации выбора может реализовываться в качественно различных вариантах
Различные сочетания
перечисленных вариантов являются основными и приводят к многообразным задачам выбора, которые изучены не в одинаковой степени1. Множество альтернатив может быть конечным, счетным или континуальным
2. Оценка альтернативы может осуществляться по одному или по нескольким критериям, которые в свою очередь могут иметь как количественный, так и качественный характер
3. Режим выбора может быть однократным (разовым) или повторяющимся, допускающим обучение на опыте
4. Последствия выбора могут быть точно известны (выбор в условиях определенности), иметь вероятностный характер, когда известны вероятности возможных исходов после сделанного выбора (выбор в условиях риска), или иметь неоднозначный исход, не допускающий введения вероятностей (выбор в условиях неопределенности)
5. Ответственность за выбор может быть односторонней (в частном случае индивидуальной) или многосторонней. Соответственно различают индивидуальный и групповой выбор
6. Степень согласованности целей при многостороннем выборе может варьироваться от полного совпадения интересов сторон (кооперативный выбор) до их противоположности (выбор в конфликтной ситуации). Возможны также промежуточные случаи, например компромиссный выбор, коалиционный выбор, выбор в условиях нарастающего конфликта и т.д.
1. Множество альтернатив
2. Оценка альтернативы
4. Последствия выбора
3. Режим выбора
5. Ответственность за выбор
6. Степень согласованности целей
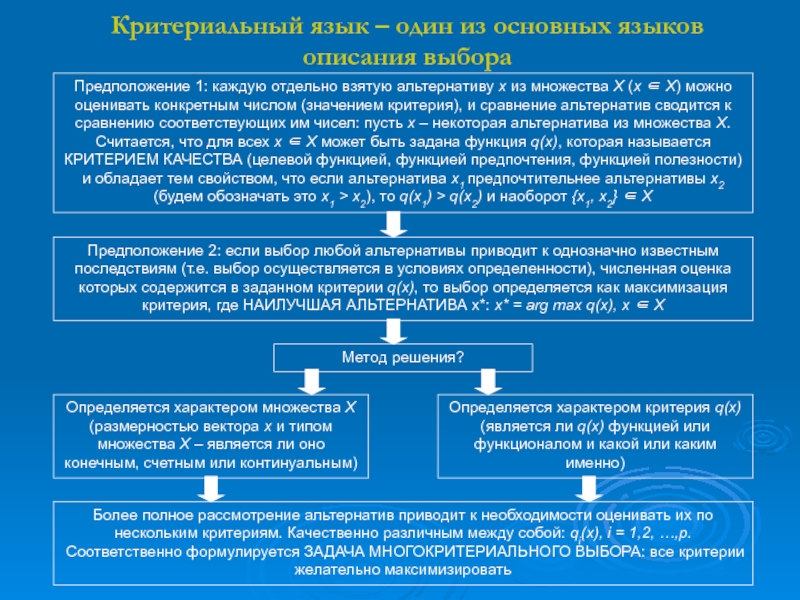
Слайд 5Критериальный язык – один из основных языков описания выбора
Предположение 1:
каждую отдельно взятую альтернативу х из множества Х (х
Х) можно оценивать конкретным числом (значением критерия), и сравнение альтернатив сводится к сравнению соответствующих им чисел: пусть х – некоторая альтернатива из множества Х. Считается, что для всех х Х может быть задана функция q(x), которая называется КРИТЕРИЕМ КАЧЕСТВА (целевой функцией, функцией предпочтения, функцией полезности) и обладает тем свойством, что если альтернатива х1 предпочтительнее альтернативы х2 (будем обозначать это х1 > х2), то q(x1) > q(x2) и наоборот {x1, x2} XПредположение 2: если выбор любой альтернативы приводит к однозначно известным последствиям (т.е. выбор осуществляется в условиях определенности), численная оценка которых содержится в заданном критерии q(x), то выбор определяется как максимизация критерия, где НАИЛУЧШАЯ АЛЬТЕРНАТИВА x*: x* = arg max q(x), x X
Более полное рассмотрение альтернатив приводит к необходимости оценивать их по нескольким критериям. Качественно различным между собой: qi(x), i = 1,2, …,p. Соответственно формулируется ЗАДАЧА МНОГОКРИТЕРИАЛЬНОГО ВЫБОРА: все критерии желательно максимизировать
Метод решения?
Определяется характером множества Х (размерностью вектора х и типом множества Х – является ли оно конечным, счетным или континуальным)
Определяется характером критерия q(x) (является ли q(x) функцией или функционалом и какой или каким именно)
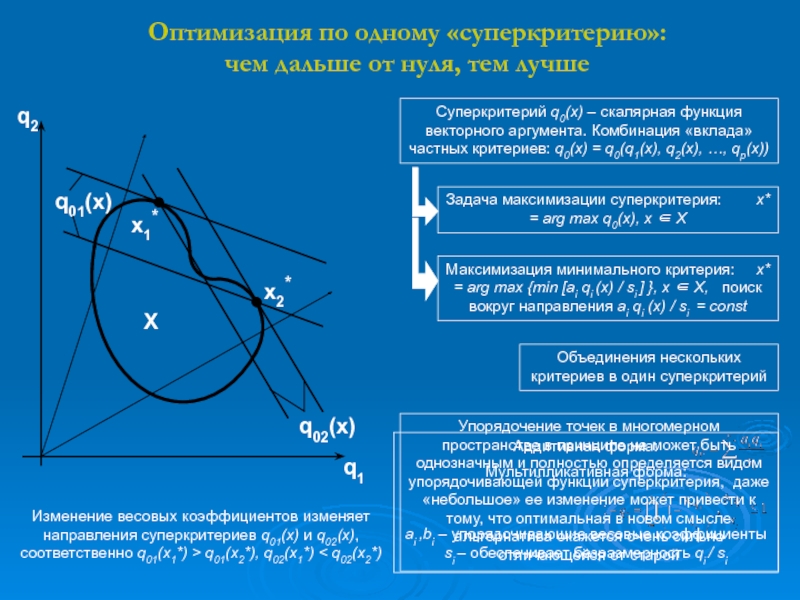
Слайд 6Оптимизация по одному «суперкритерию»:
чем дальше от нуля, тем лучше
Суперкритерий
q0(x) – скалярная функция векторного аргумента. Комбинация «вклада» частных критериев: q0(x) = q0(q1(x), q2(x), …, qp(x))Задача максимизации суперкритерия: х* = arg max q0(x), x X
Максимизация минимального критерия: х* = arg max {min [ai qi (x) / si ] }, x X, поиск вокруг направления ai qi (x) / si = const
Аддитивная форма:
Мультипликативная форма:
ai ,bi – упорядочивающие весовые коэффициенты si – обеспечивает безразмерность qi / si
Объединения нескольких критериев в один суперкритерий
Упорядочение точек в многомерном пространстве в принципе не может быть однозначным и полностью определяется видом упорядочивающей функции суперкритерия, даже «небольшое» ее изменение может привести к тому, что оптимальная в новом смысле альтернатива окажется очень сильно отличающейся от старой
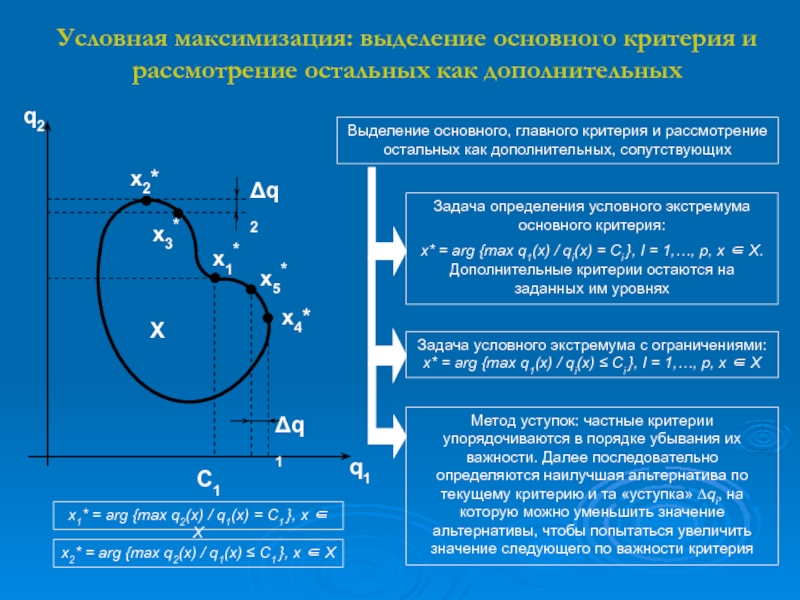
Слайд 7Условная максимизация: выделение основного критерия и рассмотрение остальных как дополнительных
Выделение
основного, главного критерия и рассмотрение остальных как дополнительных, сопутствующих
x1* =
arg {max q2(x) / q1(x) = C1 }, x Xx2* = arg {max q2(x) / q1(x) ≤ C1 }, x X
Метод уступок: частные критерии упорядочиваются в порядке убывания их важности. Далее последовательно определяются наилучшая альтернатива по текущему критерию и та «уступка» ∆qi, на которую можно уменьшить значение альтернативы, чтобы попытаться увеличить значение следующего по важности критерия
Задача условного экстремума с ограничениями: x* = arg {max q1(x) / qi(x) ≤ Ci }, I = 1,…, p, x X
Задача определения условного экстремума основного критерия:
x* = arg {max q1(x) / qi(x) = Ci }, I = 1,…, p, x X. Дополнительные критерии остаются на заданных им уровнях
x2*
q2
x4*
q1
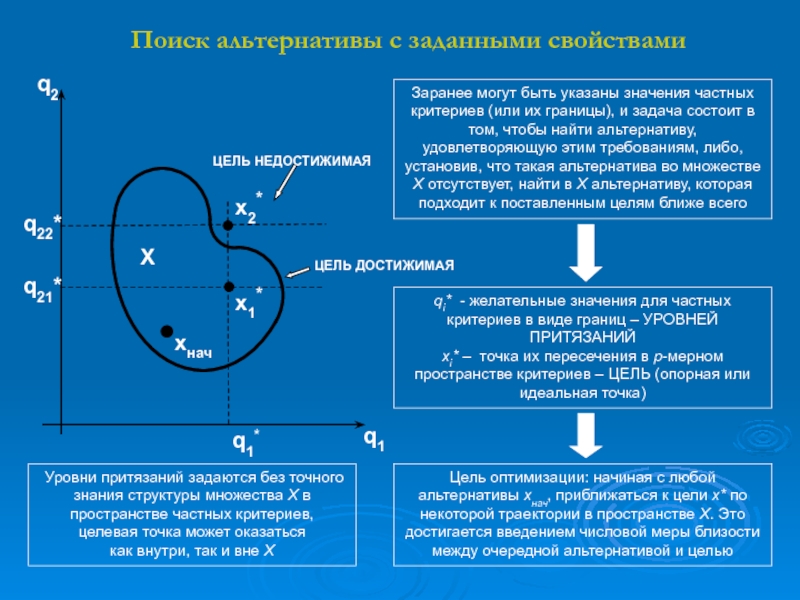
Слайд 8Поиск альтернативы с заданными свойствами
xнач
Цель оптимизации: начиная с любой альтернативы
хнач, приближаться к цели х* по некоторой траектории в пространстве
Х. Это достигается введением числовой меры близости между очередной альтернативой и цельюq21*
q22*
Заранее могут быть указаны значения частных критериев (или их границы), и задача состоит в том, чтобы найти альтернативу, удовлетворяющую этим требованиям, либо, установив, что такая альтернатива во множестве X отсутствует, найти в X альтернативу, которая подходит к поставленным целям ближе всего
Уровни притязаний задаются без точного
знания структуры множества Х в пространстве частных критериев,
целевая точка может оказаться
как внутри, так и вне Х
qi* - желательные значения для частных критериев в виде границ – УРОВНЕЙ ПРИТЯЗАНИЙ xi* – точка их пересечения в р-мерном пространстве критериев – ЦЕЛЬ (опорная или идеальная точка)
Слайд 9Определение паретовского множества альтернатив
- Множество Парето
q10, q20 – примеры выбора
единственных альтернатив
Отказ от выделения единственной «наилучшей» альтернативы
Соглашение: предпочтение одной альтернативе
перед другой можно отдавать, только если первая по всем критериям лучше второй, иначе альтернативы несравнимыеЕсли все максимально достижимые значения частных критериев не относятся к одной альтернативе, то такие альтернативы образуют множество Парето
Для выбора единственной альтернативы формулируются дополнительные критерии и ограничения
В результате попарного сравнения альтернатив все худшие по всем критериям альтернативы отбрасываются, а все оставшиеся несравнимые между собой (недоминируемые) принимаются
q20
q10
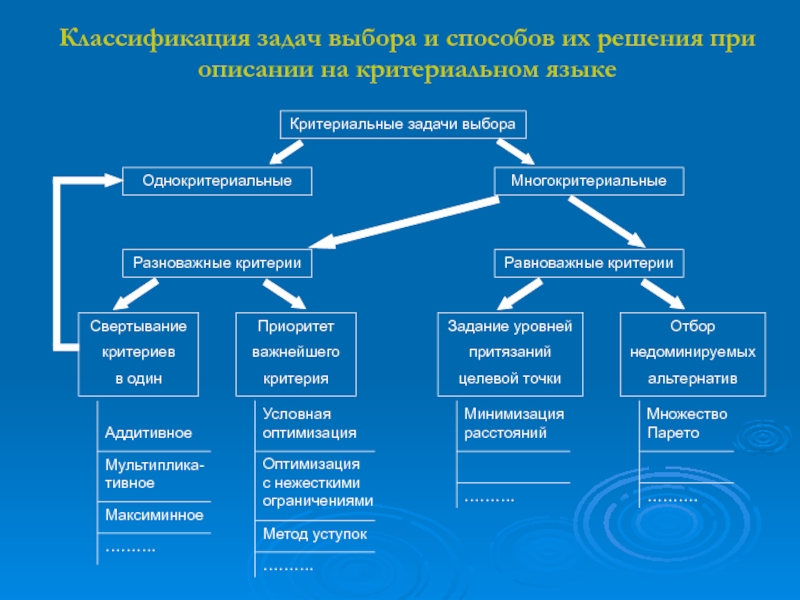
Слайд 10Классификация задач выбора и способов их решения при описании на
критериальном языке
Критериальные задачи выбора
Многокритериальные
Однокритериальные
Отбор
недоминируемых
альтернатив
Приоритет
важнейшего
критерия
Свертывание
критериев
в один
Аддитивное
Условная
оптимизация
Оптимизация
с нежесткими
ограничениями
Метод уступок
Разноважные критерии
Равноважные критерии
Задание
уровнейпритязаний
целевой точки
Мультиплика-тивное
Минимизация
расстояний
Множество
Парето
Максиминное
……….
……….
……….
……….
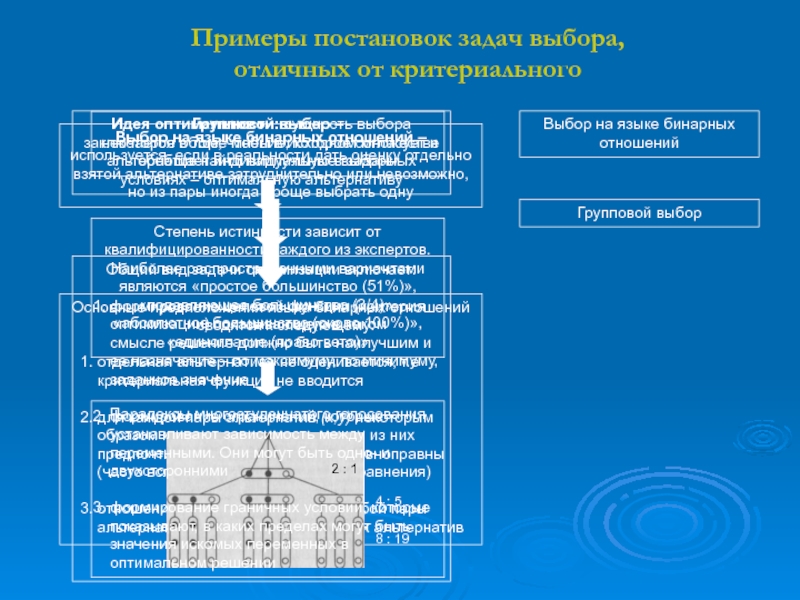
Слайд 11Примеры постановок задач выбора,
отличных от критериального
Выбор на языке бинарных
отношений – используется, если в реальности дать оценку отдельно взятой
альтернативе затруднительно или невозможно, но из пары иногда проще выбрать однуОсновные предположения языка бинарных отношений сводятся к следующему:
1. отдельная альтернатива не оценивается, т.е критериальная функция не вводится
2. для каждой пары альтернатив (x,y) некоторым образом можно установить, что одна из них предпочтительнее другой или они равноправны (часто вследствие невозможности сравнения)
3. отношения предпочтения внутри любой пары альтернатив не зависят от остальных альтернатив
Групповой выбор –
некоторое общее мнение, которое согласует и обобщает индивидуальные выборы
Степень истинности зависит от квалифицированности каждого из экспертов. Наиболее распространенными вариантами являются «простое большинство (51%)», «подавляющее большинство (3/4)», «абсолютное большинство (около 100%)», «единогласие (право вето)»
Парадоксы многоступенчатого голосования
2 : 1
4 : 5
8 : 19
Идея оптимальности: сущность выбора заключается в том, чтобы в исходном множестве альтернатив найти наилучшую в заданных условиях – оптимальную альтернативу
Общий вид задачи оптимизации включает:
1. формирование целевой функции (критерия оптимизации) показывающего в каком смысле решение должно быть наилучшим и ее назначение – по максимуму, по минимуму, заданное значение
2. формирование ограничений, которые устанавливают зависимость между переменными. Они могут быть одно- и двухсторонними
3. формирование граничных условий, которые показывают, в каких пределах могут быть значения искомых переменных в оптимальном решении
Выбор на языке бинарных отношений
Групповой выбор
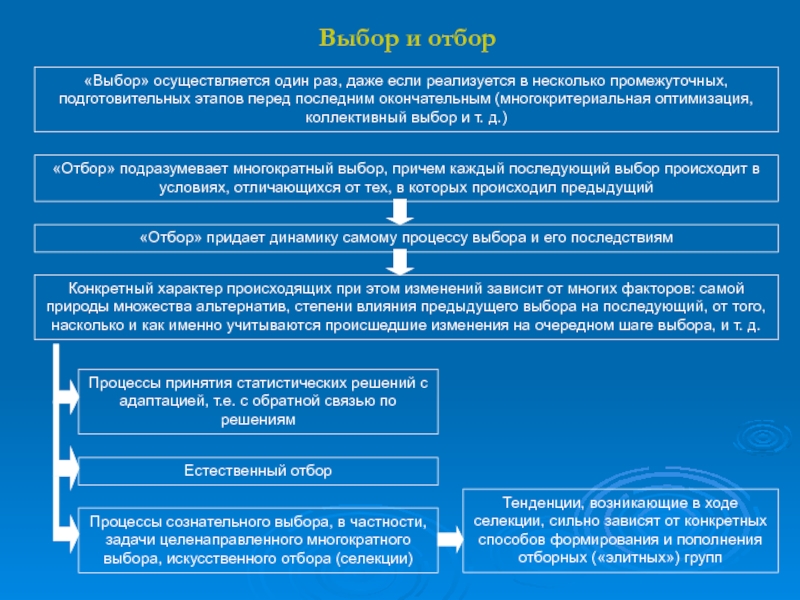
Слайд 12Выбор и отбор
«Выбор» осуществляется один раз, даже если реализуется в
несколько промежуточных, подготовительных этапов перед последним окончательным (многокритериальная оптимизация, коллективный
выбор и т. д.)«Отбор» подразумевает многократный выбор, причем каждый последующий выбор происходит в условиях, отличающихся от тех, в которых происходил предыдущий
«Отбор» придает динамику самому процессу выбора и его последствиям
Конкретный характер происходящих при этом изменений зависит от многих факторов: самой природы множества альтернатив, степени влияния предыдущего выбора на последующий, от того, насколько и как именно учитываются происшедшие изменения на очередном шаге выбора, и т. д.
Процессы принятия статистических решений с адаптацией, т.е. с обратной связью по решениям
Естественный отбор
Процессы сознательного выбора, в частности, задачи целенаправленного многократного выбора, искусственного отбора (селекции)
Тенденции, возникающие в ходе селекции, сильно зависят от конкретных способов формирования и пополнения отборных («элитных») групп
Слайд 13Введение в теорию «элитных групп»
Из исходного множества элементов в соответствии
с заданным показателем качества и правилом выбора наиболее предпочтительного элемента
(при равном показателе качества) формируется «элитная группа» заданного размераВ «элитную группу» с небольшой вероятностью могут попадать и «сорные элементы», однако после своего формирования эта группа может использоваться для выполнения задачи
При формировании и работе с «элитной группой»:
1. доля элементов, отвечающих требованиям элитности, но не попавшая в «элитную группу»
3. правило отсева из «элитной группы»
4. правило новых включений в «элитную группу»
Примеры наиболее распространенных процедур работы с «элитными группами»:
1. Правило «претедент-рекомендатель» означает, что случайно из множества элементов вне «элитной группы» выбирается «претендент», а из «элитной группы» «рекомендатель». Если претендент не хуже рекомендателя, то они меняются местами
5. временные соотношения между моментами новых включений и характерными временами изменения элементов
2. характер изменения качества элементов и внутри и вне «элитной группы»
2. Правило «прополка» (основная активность внутри «элитной группы») означает удаление из «элитной группы» m наихудших и заменой их на m случайных из тех, что вне «элитной группы», причем наилучшие показатели прогресса «элитной группы» достигаются при m =1
3. Правило «делегирования» (основная активность вне «элитной группы») означает выбор N элементов вне «элитной группы», их упорядочивание по качеству и зачисление в «элитную группу» элемента с лучшим качеством. Для повышения качества «элитной группы» объем выборки «делегирования» вне «элитной группы» должен быть наибольшим