Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция № 4 Кинематическое исследование механизмов построением планов скоростей
Содержание
- 1. Лекция № 4 Кинематическое исследование механизмов построением планов скоростей
- 2. Построение кинематической схемы кривошипно-ползунного механизмаПоложение ползуна в
- 3. Построение плана скоростей кривошипно-ползунного механизмаabВедущее звено (кривошипа)
- 4. Свойства плана скоростейОтрезки плана скоростей, проходящие через
- 5. Построение плана ускорений КПМa Нормальное ускорение
- 6. Свойство плана ускоренийОтрезки планов ускорений проходящие через
- 7. Кинематический анализ кулисного механизмаКривошип О1А совершает вращательное
- 8. Построение плана ускоренийУскорение точки А звена 2
- 9. План скоростей рычажного механизмаa b
- 10. План ускорений рычажного механизма Нормальное ускорение ведущего
- 11. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1
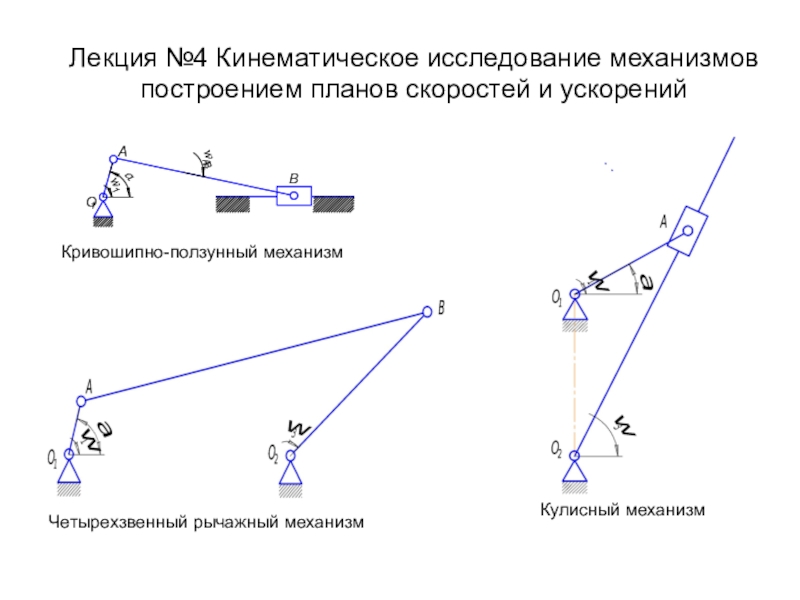
Лекция №4 Кинематическое исследование механизмов построением планов скоростей и ускорений
Кривошипно-ползунный
механизм
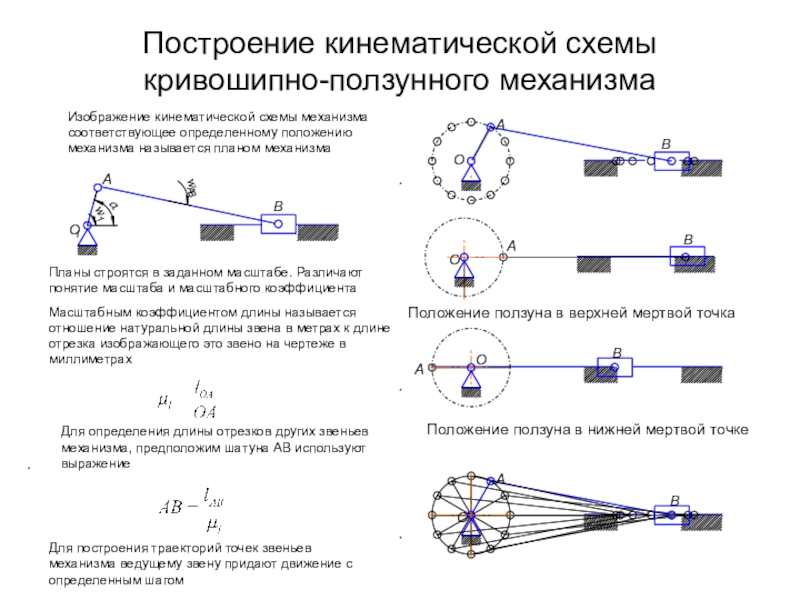
Слайд 2Построение кинематической схемы кривошипно-ползунного механизма
Положение ползуна в верхней мертвой точка
Положение
ползуна в нижней мертвой точке
O
A
B
Масштабным коэффициентом длины называется отношение натуральной длины звена в метрах к длине отрезка изображающего это звено на чертеже в миллиметрах
Изображение кинематической схемы механизма соответствующее определенному положению механизма называется планом механизма
Планы строятся в заданном масштабе. Различают понятие масштаба и масштабного коэффициента
Для определения длины отрезков других звеньев механизма, предположим шатуна АВ используют выражение
Для построения траекторий точек звеньев механизма ведущему звену придают движение с определенным шагом
Слайд 3Построение плана скоростей кривошипно-ползунного механизма
a
b
Ведущее звено (кривошипа) совершает вращательное движение
относительно О и окружная скорость равна
Масштабом скорости называется отношение окружной
скорости ведущего звена VA в м/с к длине отрезка pVa изображающего данную скорость на плане скоростей в ммШатун АВ совершает плоскопараллельное движение и векторное уравнение для определения скорости точки В запишется в следующем виде
Для скоростей VВА и VВ известно только направление VB - направлена вдоль направляющей; VBA направлена перпендикулярно звену АВ)
Направлена перпендикулярно кривошипу ОА
Построение треугольников скоростей, выполненных на отдельном участке чертежа и произведенное от одной общей точки называется планом скоростей
Полюсом плана скоростей называется произвольная точка плоскости чертежа из которой производится построение плана скоростей
Имея план скоростей легко определить скорости звеньев
Слайд 4Свойства плана скоростей
Отрезки плана скоростей, проходящие через полюс, изображают абсолютные
скорости. Направление абсолютных скоростей всегда получается от полюса. В конце
векторов абсолютных скоростей принято ставить малую букву той буквы, которой обозначается соответствующая точка на плане механизма;Отрезки плана скоростей , не проходящие через полюс , обозначают относительные скорости;
Концы векторов абсолютных скоростей точек механизма жестко связанных между собой, на плане скоростей образуют фигуры, подобные сходственно расположенные и повернутые на 90 градусов относительно фигур, образуемых этими точками на плане механизма
Неподвижные точки механизма имеют соответствующие им точки на плане скоростей расположенные в полюсе
План скоростей дает возможность находить нормали и касательные к траектории точки без построения самих траекторий
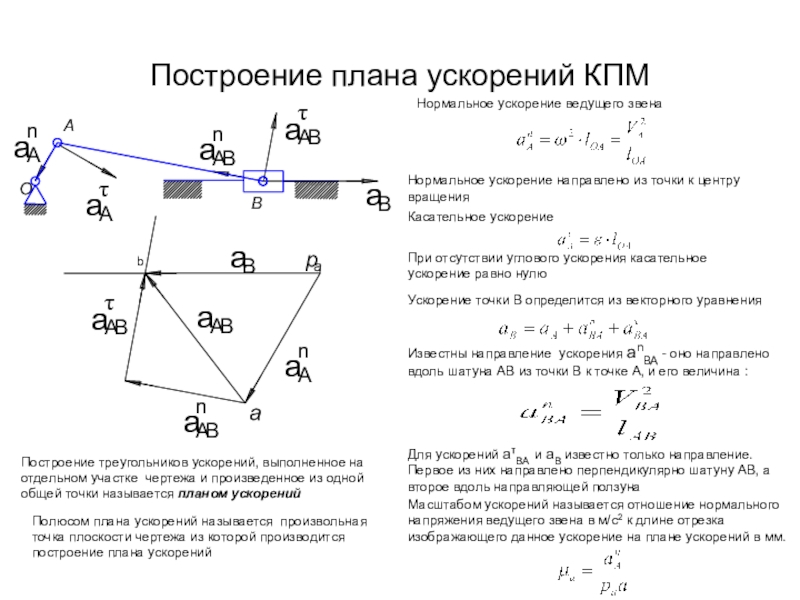
Слайд 5Построение плана ускорений КПМ
a
Нормальное ускорение ведущего звена
Нормальное ускорение
направлено из точки к центру вращения
Касательное ускорение
При отсутствии углового ускорения
касательное ускорение равно нулюУскорение точки В определится из векторного уравнения
Известны направление ускорения аnВА - оно направлено вдоль шатуна АВ из точки В к точке А, и его величина :
Для ускорений аВА и аВ известно только направление. Первое из них направлено перпендикулярно шатуну АВ, а второе вдоль направляющей ползуна
Построение треугольников ускорений, выполненное на отдельном участке чертежа и произведенное из одной общей точки называется планом ускорений
Полюсом плана ускорений называется произвольная точка плоскости чертежа из которой производится построение плана ускорений
Масштабом ускорений называется отношение нормального напряжения ведущего звена в м/с2 к длине отрезка изображающего данное ускорение на плане ускорений в мм.
b
Слайд 6Свойство плана ускорений
Отрезки планов ускорений проходящие через полюс изображают абсолютные
ускорения. Направление абсолютных ускорений всегда получается от полюса. В конце
векторов абсолютных ускорений принято ставить малую букву, той буквы которой обозначена соответствующая точка на плане механизма;Отрезки плана ускорений соединяющие концы векторов абсолютных ускорений, обозначают относительные ускорения;
Концы векторов абсолютных ускорений точек механизма жестко связанных между собой на плане ускорений образуют фигуры подобные, сходственно расположенные и повернутые на угол 180- относительно расположения их на плане механизма;
Постоянные неподвижные точки механизма имеют соответствующие им точки плана ускорений расположенные в полюсе;
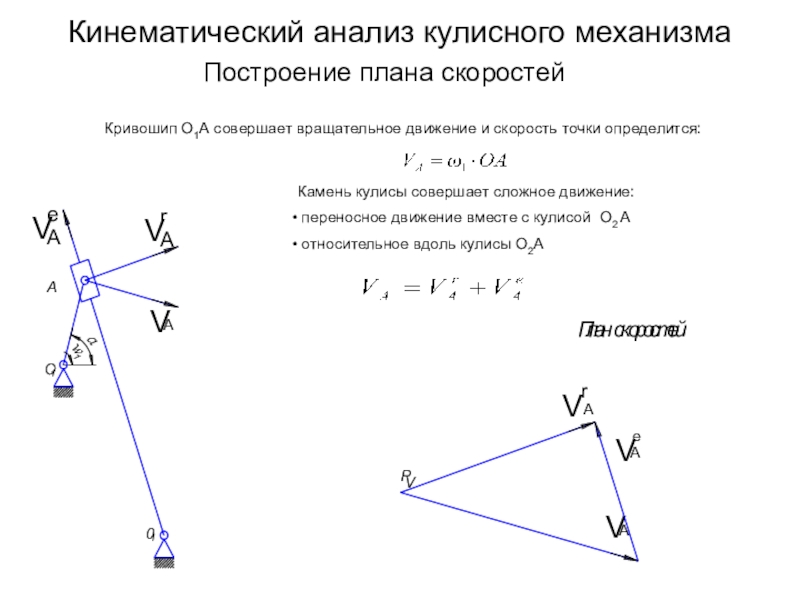
Слайд 7Кинематический анализ кулисного механизма
Кривошип О1А совершает вращательное движение и скорость
точки определится:
Камень кулисы совершает сложное движение:
переносное движение вместе с
кулисой О2 А относительное вдоль кулисы О2А
Построение плана скоростей
Слайд 8Построение плана ускорений
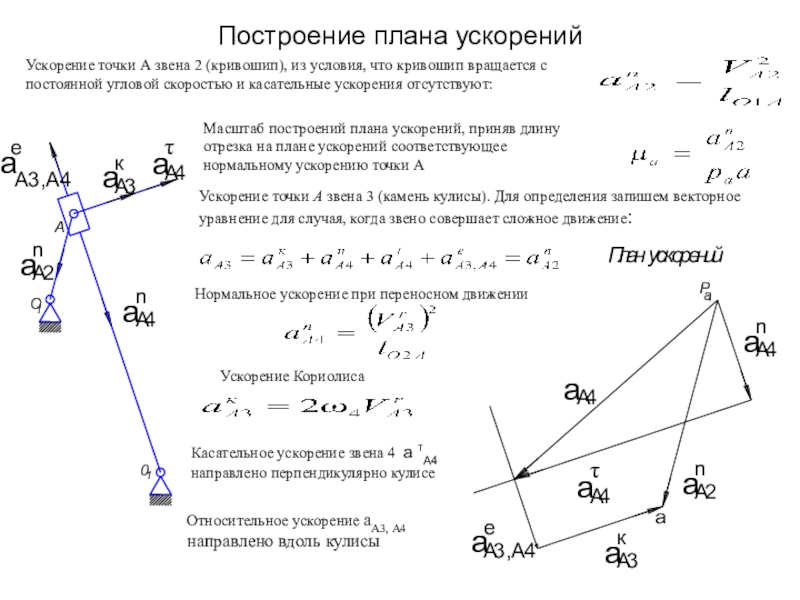
Ускорение точки А звена 2 (кривошип), из условия,
что кривошип вращается с постоянной угловой скоростью и касательные ускорения
отсутствуют:Масштаб построений плана ускорений, приняв длину отрезка на плане ускорений соответствующее нормальному ускорению точки А
Ускорение точки А звена 3 (камень кулисы). Для определения запишем векторное уравнение для случая, когда звено совершает сложное движение:
Нормальное ускорение при переносном движении
Ускорение Кориолиса
а
Касательное ускорение звена 4 а А4 направлено перпендикулярно кулисе
Относительное ускорение аА3, А4 направлено вдоль кулисы
Слайд 9План скоростей рычажного механизма
a
b
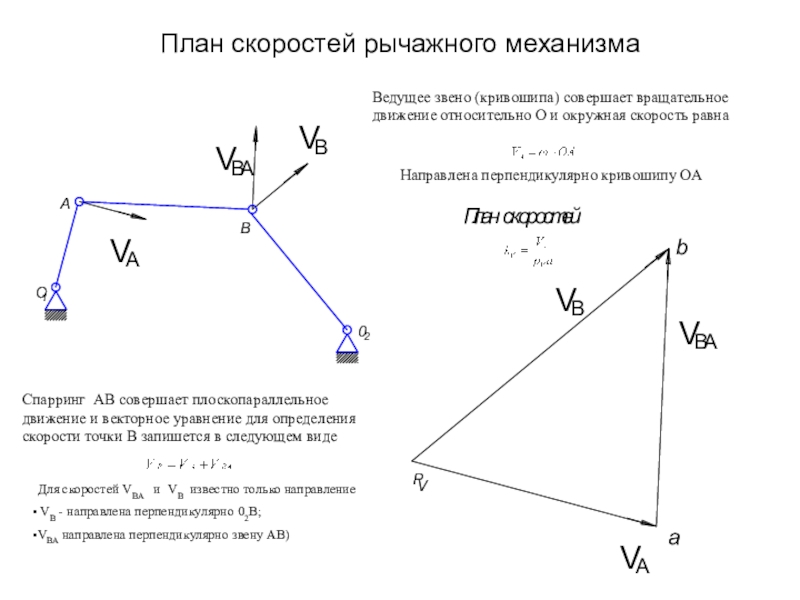
Ведущее звено (кривошипа)
совершает вращательное движение относительно О и окружная скорость равна
Направлена перпендикулярно
кривошипу ОАСпарринг АВ совершает плоскопараллельное движение и векторное уравнение для определения скорости точки В запишется в следующем виде
Для скоростей VВА и VВ известно только направление
VВ - направлена перпендикулярно 02В;
VВА направлена перпендикулярно звену АВ)
Слайд 10План ускорений рычажного механизма
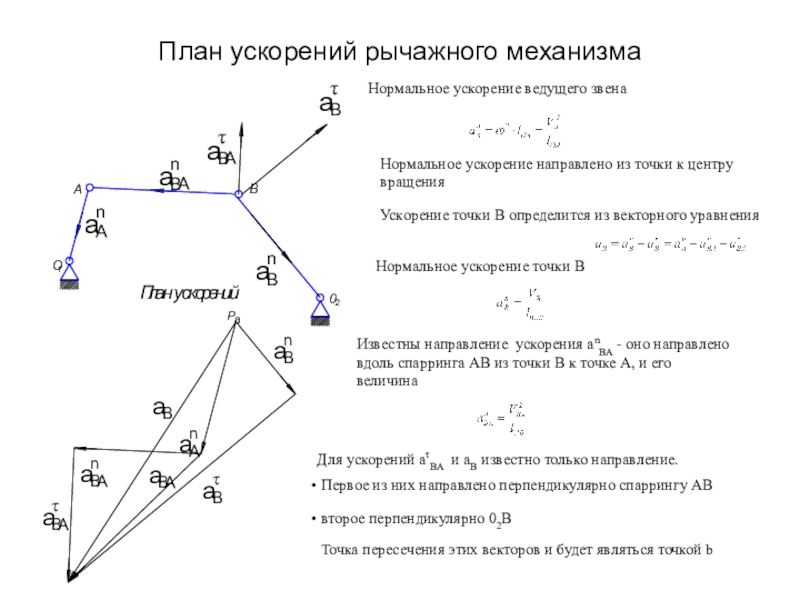
Нормальное ускорение ведущего звена
Нормальное ускорение направлено
из точки к центру вращения
Ускорение точки В определится из векторного
уравненияИзвестны направление ускорения аnВА - оно направлено вдоль спарринга АВ из точки В к точке А, и его величина
Для ускорений аВА и аB известно только направление.
Первое из них направлено перпендикулярно спаррингу АВ
второе перпендикулярно 02В
Точка пересечения этих векторов и будет являться точкой b
Нормальное ускорение точки В