Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция №19 Спектры непериодических сигналов
Содержание
- 1. Лекция №19 Спектры непериодических сигналов
- 2. С увеличением периода сигнала Т спектральные линии
- 3. Слайд 3
- 4. Слайд 4
- 5. - спектральная плотность сигнала
- 6. Прямое преобразование Фурье:позволяет определить спектральную плотность сигнала
- 7. Обратное преобразование Фурье: позволяет определить сигнал по его спектральной плотности
- 8. Слайд 8
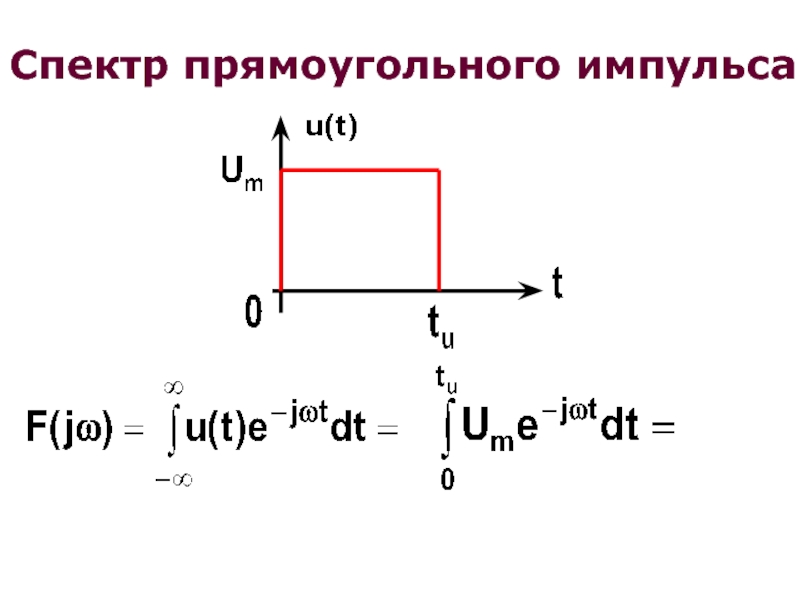
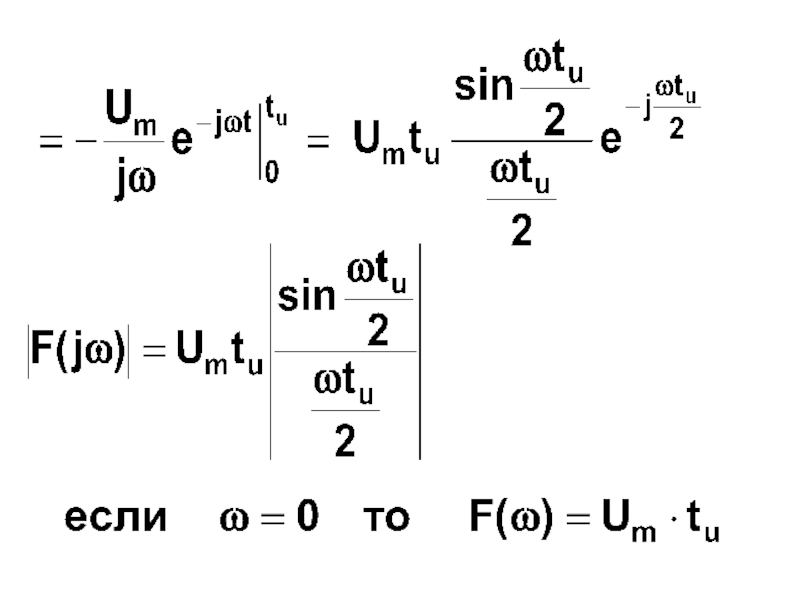
- 9. Спектр прямоугольного импульса
- 10. Слайд 10
- 11. нули:
- 12. - спектр сплошной
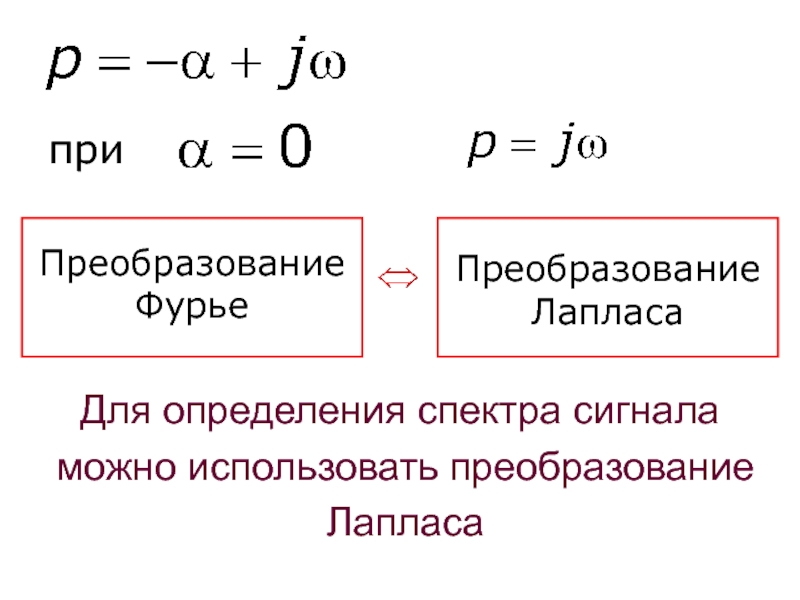
- 13. Одностороннее преобразование Фурье. Связь с преобразованием ЛапласаЕсли при- одностороннее преобразование Фурье
- 14. преобразования Лапласа:
- 15. приПреобразование ЛапласаПреобразование ФурьеДля определения спектра сигнала можно использовать преобразование Лапласа
- 16. 1) Спектр импульса включения
- 17. 2) Спектр -импульса
- 18. ТЕОРЕМЫ О СПЕКТРАХ 1. теорема линейности2. теорема запаздыванияСпектральная плотность амплитуд не меняется, меняется только спектральная плотность фаз
- 19. 3. теорема дифференцирования - если - еслиДифференцирование сигнала ведет к расширению его спектра
- 20. 4. теорема интегрирования - нулевые
- 21. 5. Теорема подобия6. Теорема смещенияЧем короче импульс,
- 22. 7. Теорема свертки
- 23. 8. Равенство Парсеваля (теорема Релея) Энергия сигнала во временной области равна энергии сигнала в частотной области
- 24. энергия электрического сигнала, рассеиваемая на сопротивлении
- 25. позволяет судить об распределении энергии в спектре непериодического сигналаРавенство Парсеваля применяют для выбора полосы пропускания канала
- 26. выбирают из условия передачи 90% энергии сигналаНайдем для прямоугольного импульса
- 27. Слайд 27
- 28. Ширина спектра равна ширине основного лепестка и обратно-пропорциональна длительности импульса
- 29. Скачать презентанцию
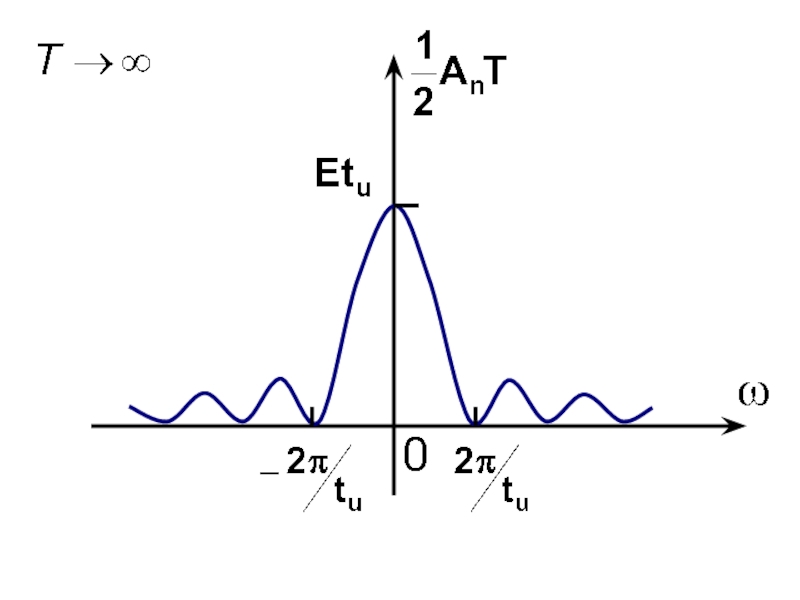
С увеличением периода сигнала Т спектральные линии сгущаются а их амплитуды уменьшаются. При периодическая последовательность переходит в одиночный импульс. Спектральные линии такого импульса сольются друг
Слайды и текст этой презентации
Слайд 13Одностороннее преобразование Фурье. Связь с преобразованием Лапласа
Если при
-
одностороннее преобразование Фурье
Слайд 15при
Преобразование Лапласа
Преобразование Фурье
Для определения спектра сигнала
можно использовать преобразование
Лапласа
Слайд 18ТЕОРЕМЫ О СПЕКТРАХ
1. теорема линейности
2. теорема запаздывания
Спектральная плотность амплитуд не меняется,
меняется только спектральная плотность фаз
Слайд 19 3. теорема дифференцирования
- если
- если
Дифференцирование
сигнала ведет
к расширению его спектра
Слайд 20 4. теорема интегрирования
- нулевые начальные условия
-
ненулевые начальные условия
Интегрирование сигнала ведет
к сужению его спектра
Слайд 215. Теорема подобия
6. Теорема смещения
Чем короче импульс,
тем шире его
спектр
При умножении сигнала на
гармоническое колебание его спектр
смещается по
шкале частот на величину, равную частоте гармонического
колебания.
Слайд 238. Равенство Парсеваля (теорема Релея)
Энергия сигнала во временной области
равна энергии сигнала в частотной области
Слайд 24 энергия электрического
сигнала, рассеиваемая на сопротивлении R=1Ом
спектральная
плотность
энергии сигнала (энергетический спектр) показывает, какая доля энергии
заключена в каждой полоске частот шириной в окрестности частоты и
Слайд 25
позволяет судить об распределении энергии в спектре непериодического сигнала
Равенство Парсеваля
применяют для выбора полосы пропускания канала
Слайд 28Ширина спектра равна ширине основного лепестка и обратно-пропорциональна длительности импульса
