Lemma of force translation to a parallel position

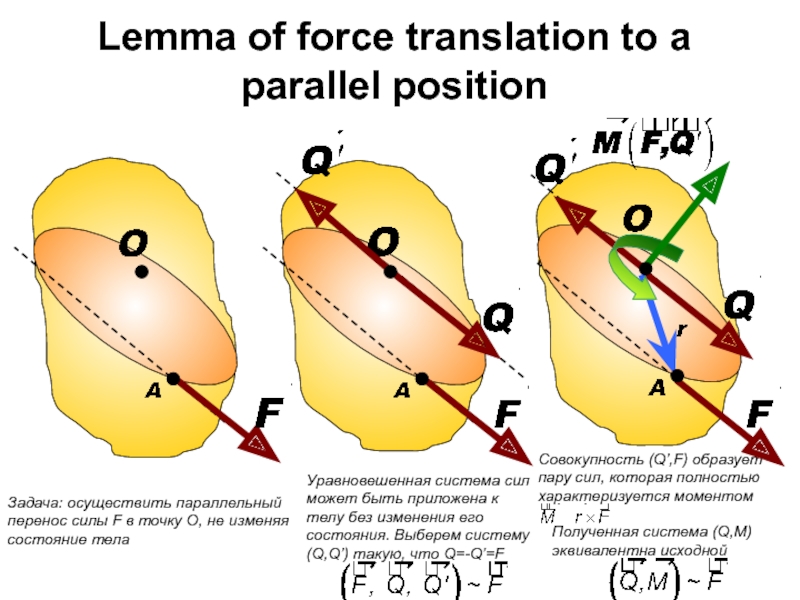
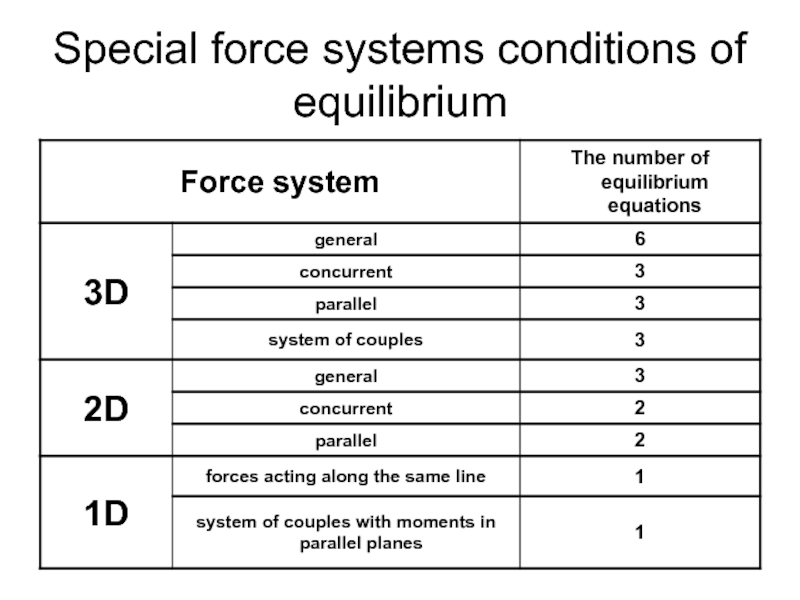
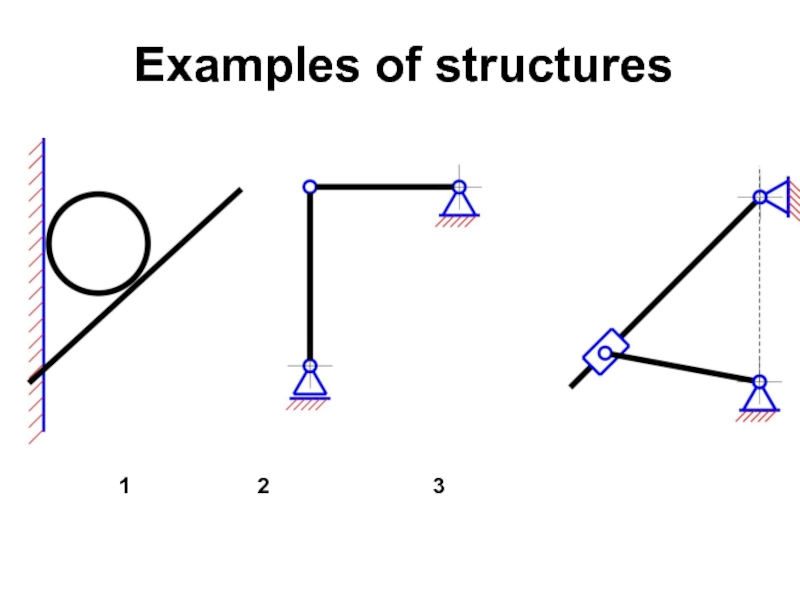
изменяя состояние тела
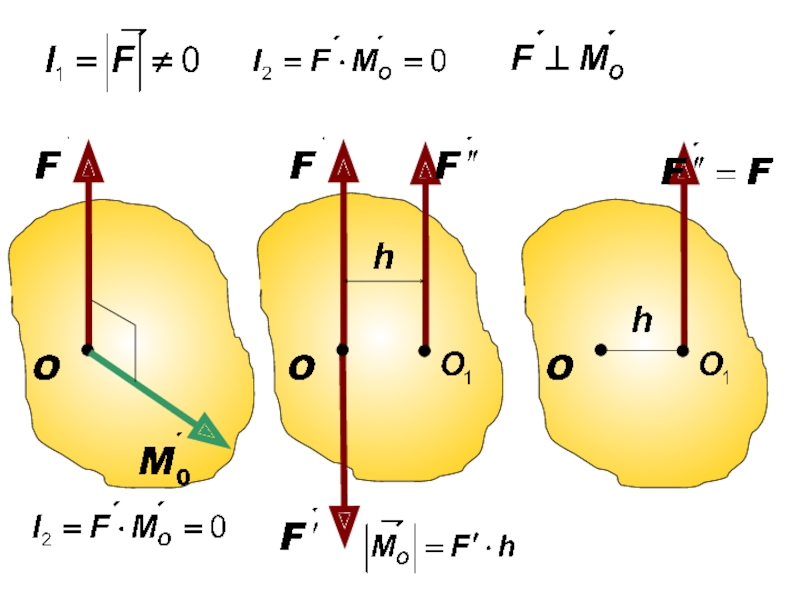
Уравновешенная система сил может быть приложена к телу

без изменения его состояния. Выберем систему (Q,Q’) такую, что Q=-Q’=F

Совокупность (Q’,F) образует пару сил, которая полностью характеризуется моментом

Lemma of force translation to a parallel position

Полученная система (Q,M) эквивалентна исходной

body is equivalent to the same force applied at the

another point of the body and couple with the moment equal to the moment of the original force with respect to the new center

Lemma of force translation to a parallel position

forces is called total vector


The vector sum of moments of

forces about a given center is called total moment about the center O

Theorem. General force system applied to a rigid body is

equivalent to a set of two elements: a force and a couple. The force is equal to the total vector and is applied at the arbitrary chosen center. The couple has vector moment equal to the total moment of original force system about chosen center.

is couple,

reduction position
For any chosen reduction center, the total vector

is equal to the vector sum of the system forces. So the total vector is independent of the reduction center position, i.e. the total vector is invariant with respect to the center of reduction.

the system is the sum of two components: original moment

about center O and moment of the total vector applied at the initial center O about the new center O1

equivalent to zero (balanced) if its total vector is zero

and total moment about chosen center O is zero:

our course are subdivided on:
Sets of bodies that simply supported.
Frames

that are engineering structures designed to support loads, frames are usually stationary fully constrained structures.
Machines that are engineering structures designed to transmit and modify forces and are structures containing moving parts.

3

Examples of structures

by destroying (sectioning) the internal constraints between the bodies of

the system.
Form FBD for each part of the system. For each adjacent part at the section apply the reactions corresponded to the type of the destroyed constraint. The direction you choose for each of the internal force components exerted on the first part is arbitrary, but you must apply equal and opposite force components of the same name to the other parts.
For each part write the equilibrium conditions taking into consideration all forces acting on the part with including reactions of destroyed internal constraints.
Analyze the statically determinacy of the problem. For the structure consisting of n members under the action of general coplanar force system it is possible to form 3n independent equations of equilibrium. If the total number of unknowns is no more than the number of independent equations (3n) the problem is statically determinate and can be solved by the methods of statics.
Solve these 3n equations as a system; check the accuracy of your solution using the equilibrium conditions for the structure as a whole.

position, i.e. total vector is invariant with respect to the

center of reduction and so the total vector magnitude is called the first statics invariant.

center the total vector is the same

, the equality means the following: for a general force system the projection of the total moment onto the line of action of the total vector is constant at any reduction center.

is called the second statics invariant.

couple moment parallel to the force is called wrench.