Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Леммы Чебышева
Содержание
- 1. Леммы Чебышева
- 2. Лемма 1.
- 3. Доказательство
- 4. Лемма 2. Тогда:- неравенство Чебышева
- 5. Доказательство
- 6. ВОПРОС 23:Закон больших чисел Чебышева
- 7. - попарно независимых случайных величин: последовательность Тогда для
- 8. Доказательство
- 9. Частный случай закона больших чисел Чебышева Тогда
- 10. ОПРЕДЕЛЕНИЕСлучайная величина сходится по вероятности к числу А если при сколь угодно малом
- 11. Частный случай закона больших чисел Чебышева – ФОРМУЛИРОВКА 2:
- 12. ВОПРОС 24:Закон больших чисел Бернулли
- 13. 1. n независимых испытаний 2. Вероятность
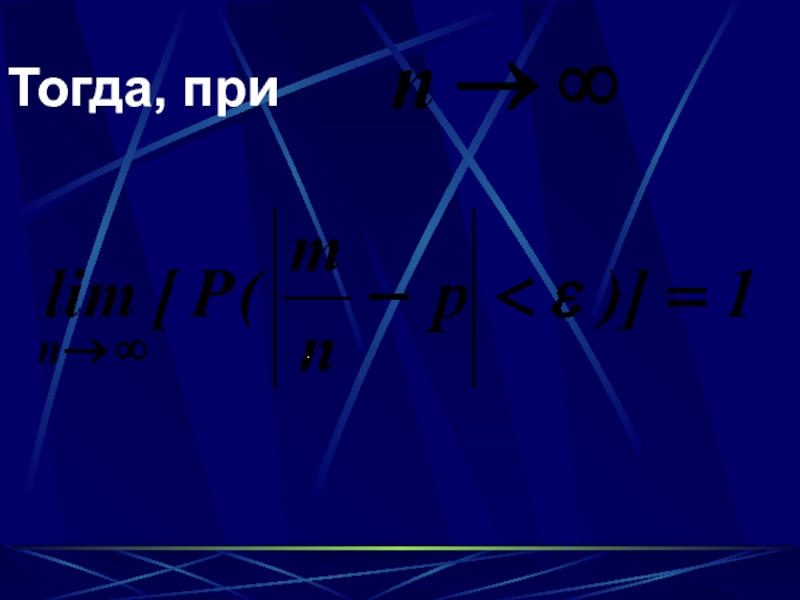
- 14. Закон больших чисел в форме Бернулли
- 15. Доказательство
- 16. Тогда, при .
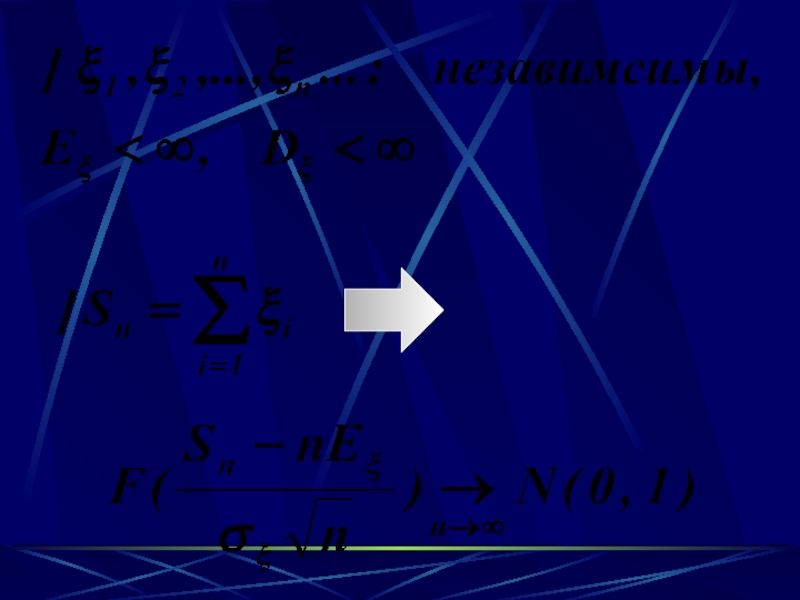
- 17. ВОПРОС 25:Классическая центральная предельная теорема
- 18. Слайд 18
- 19. Другая форма классической ЦПТ
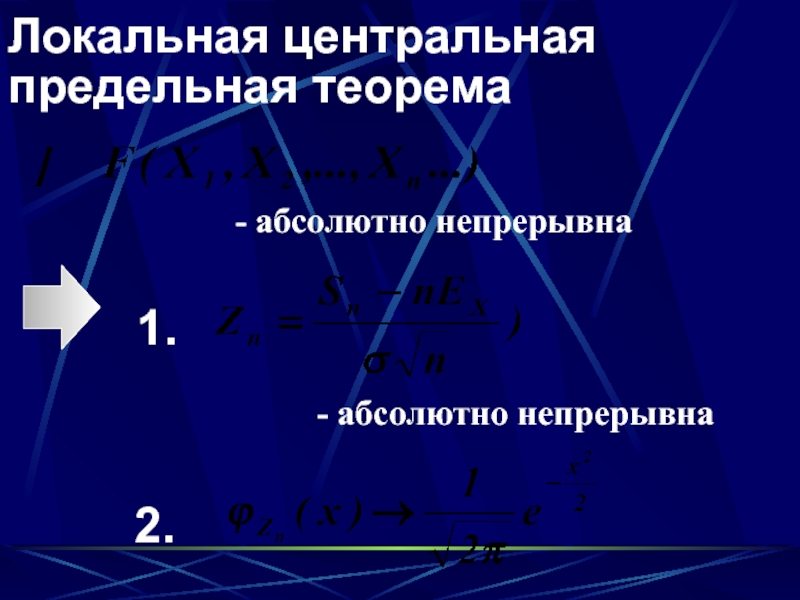
- 20. Локальная центральная предельная теорема - абсолютно непрерывна - абсолютно непрерывна 1.2.
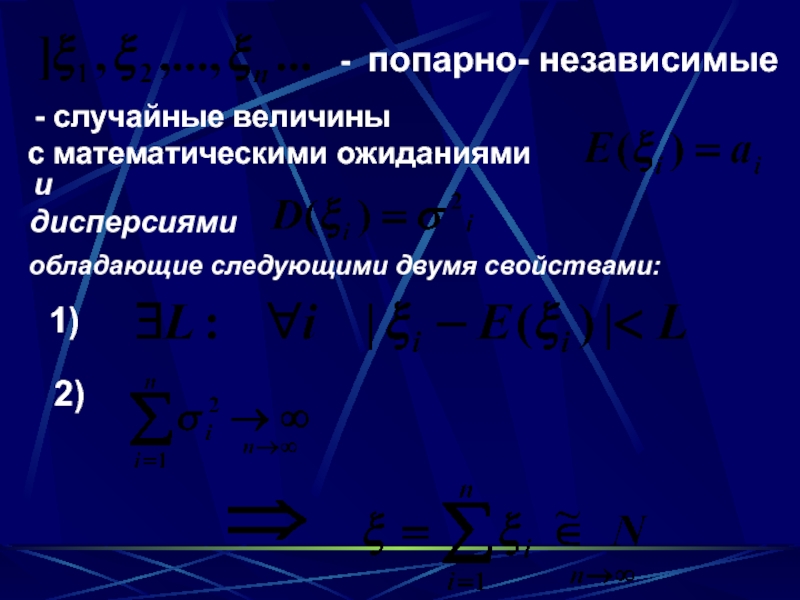
- 21. ВОПРОС 26:Теорема Ляпунова
- 22. - случайные величины с математическими ожиданиями
- 23. NB!Следствие:где Ф(х) - интеграл вероятностей где Ф(х) - интеграл вероятностей
- 24. Александр Михайлович Ляпунов (25 мая 1857, Ярославль — 3
- 25. ВОПРОС 27:Основной закон теории ошибок
- 26. Ошибки измерений в основном можно подразделить на
- 27. Основной закон ошибок:
- 28. ВОПРОС 28:Интегральная теорема Лапласа
- 29. Теорема.
- 30. Следствие:
- 31. Пример:Факультет выпускает в среднем 70% специалистов, способных
- 32. Решение.
- 33. Скачать презентанцию
Лемма 1.