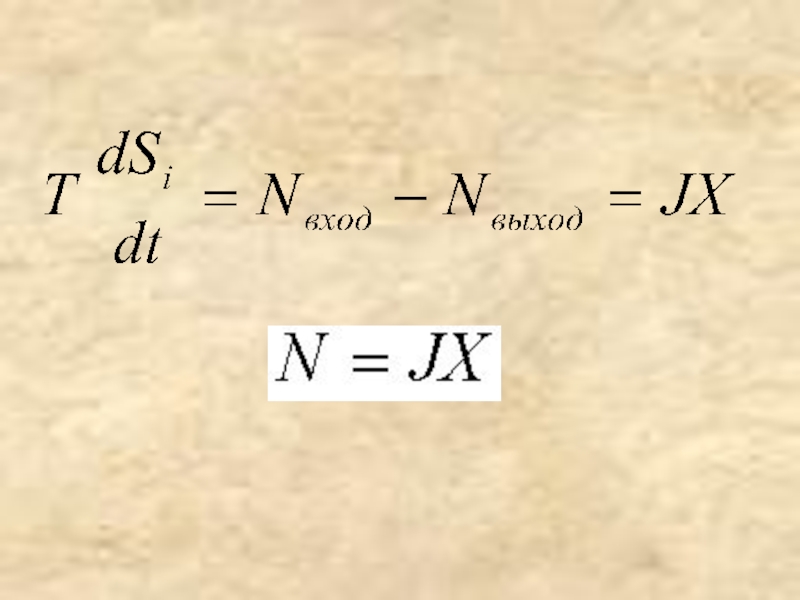Слайд 1ЛИНЕЙНАЯ НЕРАВНОВЕСНАЯ ТЕРМОДИНАМИКА
(Термодинамика открытых систем)
1. Термодинамическое равновесие и стационарное
состояние.
2. Динамика энтропии в открытых системах. Скорость продукции энтропии
и диссипативная функция. Уравнение Пригожина и его анализ.
3. Понятие обобщенной силы и потока. Примеры.
4. Теорема Пригожина.
5. Теория эволюции открытых систем Пригожина – Виам.
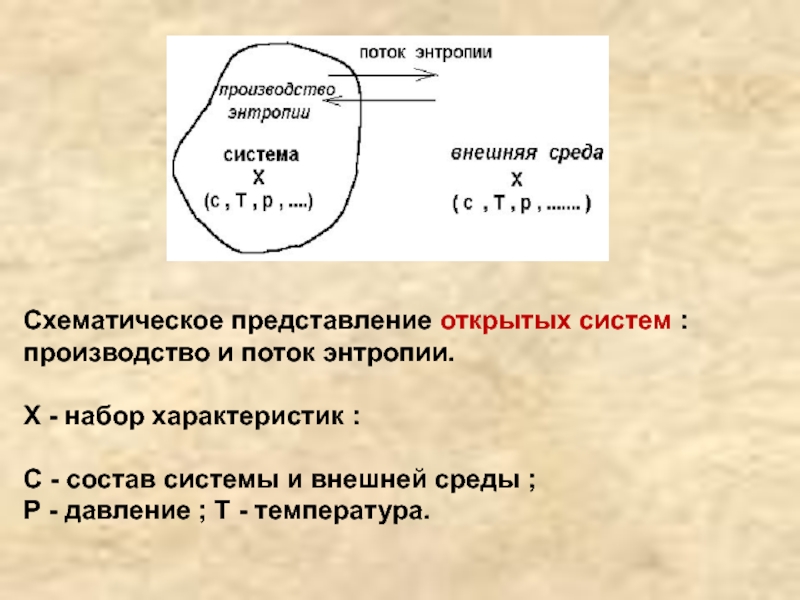
Слайд 2Схематическое представление открытых систем : производство и поток энтропии.
Х -
набор характеристик :
С - состав системы и внешней среды ;
Р
- давление ; Т - температура.
Слайд 3СТАЦИОНАРНОЕ СОСТОЯНИЕ И ТЕРМОДИНАМИЧЕСКОЕ РАВНОВЕСИЕ
ОБЩЕЕ: основные макроскопические параметры системы остаются
постоянными
Отличия
Термодинамическое равновесие Стационарное состояние
Слайд 4ИЗМЕНЕНИЕ ЭНТРОПИИ В ОТКРЫТЫХ СИСТЕМАХ
Слайд 5dS = diS + deS
Клетка - открытая система и ее
баланс энтропии выражается соотношением
Производство энтропии diS пропорционально объему 4/3 π
r3 , а отток deS пропорционален площади поверхности 4π r2
dS=A 4/3 π r3 -B 4π r2
При r = 3В/А, dS = 0
При r < 3В/А отток энтропии выше ее производства.
Когда r > 3В/А в клетке накапливаются вещества с избыточной энтропией и клетка перегревается.
Поэтому клетка должна разделиться, иначе она погибнет.
Слайд 6В системах, внутри которых протекают физические, химические, биологические процессы, всегда
производится энтропия. Это производство происходит с определенной
скоростью
Достижение термодинамики необратимых
процессов:
вводится понятие времени и рассматривается изменение энтропии во времени.
Слайд 7
ДЛЯ НЕОБРАТИМЫХ ПРОЦЕССОВ
dSe/dt может принимать разные значения
СКОРОСТЬ ПРОДУКЦИИ ЭНТРОПИИ В
ОТКРЫТЫХ СИСТЕМАХ
Слайд 8
ТОГДА
ПРОТИВОРЕЧИЕ СО ВТОРЫМ ЗАКОНОМ ТЕРМОДИНАМИКИ
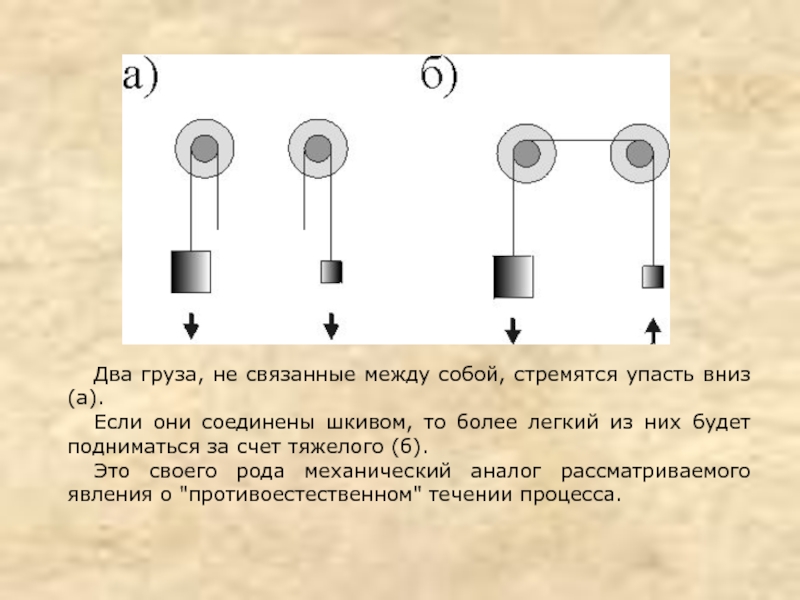
Слайд 9Два груза, не связанные между собой, стремятся упасть вниз (а).
Если
они соединены шкивом, то более легкий из них будет подниматься
за счет тяжелого (б).
Это своего рода механический аналог рассматриваемого явления о "противоестественном" течении процесса.
Слайд 11
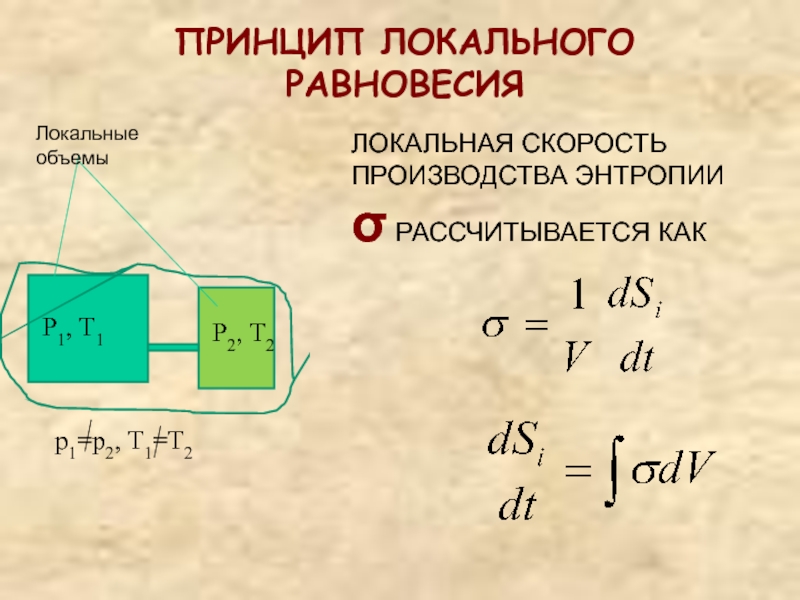
ПРИНЦИП ЛОКАЛЬНОГО РАВНОВЕСИЯ
Р1, Т1
Р2, Т2
р1=р2, Т1=Т2
Локальные объемы
ЛОКАЛЬНАЯ СКОРОСТЬ ПРОИЗВОДСТВА ЭНТРОПИИ
σ РАССЧИТЫВАЕТСЯ КАК
Слайд 12
Диссипативная функция
Для химической реакции
В обобщенном виде
Вспомним
или
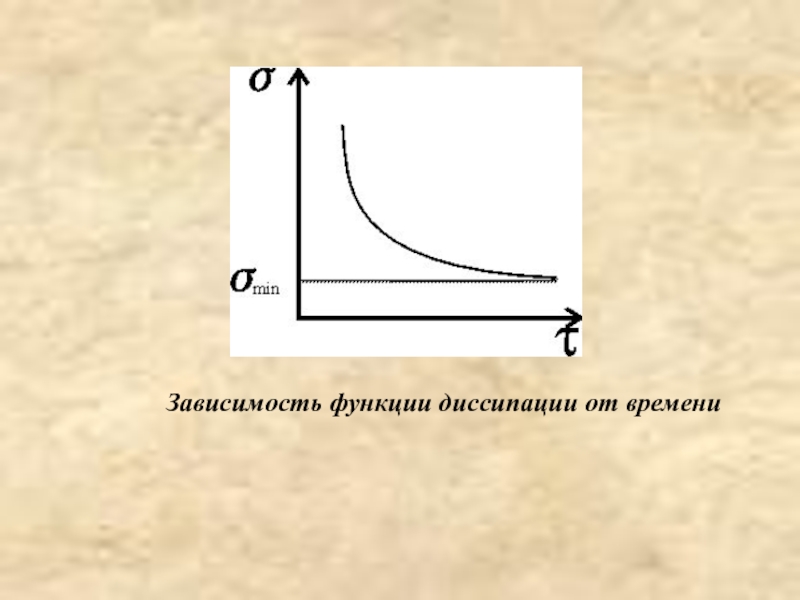
Слайд 14Зависимость функции диссипации от времени
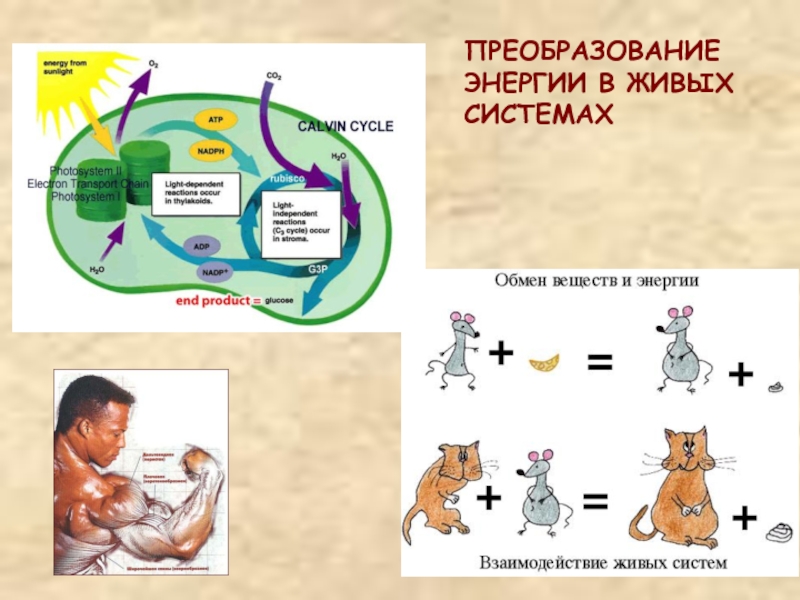
Слайд 15ПРЕОБРАЗОВАНИЕ ЭНЕРГИИ В ЖИВЫХ СИСТЕМАХ
Слайд 17СИЛЫ И ПОТОКИ В НЕРАВНОВЕСНОЙ ТЕРМОДИНАМИКЕ
Слайд 18
Закон Фика
Закон Фурье
ВБЛИЗИ ТЕРМОДИНАМИЧЕСКОГО РАВНОВЕСИЯ ПОТОКИ И СИЛЫ СВЯЗАНЫ ЛИНЕЙНО
Жан
Батист Жозеф ФУРЬЕ (1768-1830)
Адольф ФИК
1829-1901
Слайд 19В общем виде можно считать, что поток J зависит от
силы Х:
Разложим J(X) в ряд Маклорена вблизи равновесия
Здесь
Х=0 и J(0) – точка равновесия.
Производные в точке равновесия обозначим феноменологическими коэффициентами J1(0)=L
Слайд 20С учетом этих обозначений и пренебрегая членами выше первого порядка,
получим
Таким образом, вблизи термодинамического равновесия силы и потоки связаны линейной
зависимостью.
Слайд 21Ларс ОНЗАГЕР
1903 - 1976
Нобелевская премия по химии, 1968
г.
Принцип взаимности Онзагера
Слайд 23ТЕОРЕМА ПРИГОЖИНА
И.Р.Пригожин
1917 – 2003
Нобелевская премия по химии, 1977
Слайд 24
обозначим
В системе два потока: поток тепла JT и поток вещества
Слайд 26
Два условия полностью эквивалентны
В стационарном состоянии
Исследуем данную функцию на экстремум:
возьмем производную по ХM при ХT =const
Слайд 27Поскольку первая производная равна 0, значит имеется экстремум.
Найдем вторую производную
по ХМ
Это условие соответствует минимуму.
Слайд 28ТЕОРЕМА ПРИГОЖИНА
В стационарном состоянии при фиксированных внешних параметрах локальная продукция
энтропии в открытых системах стремится к минимальному значению
Tσ→min
Для конечного объема
V продукция энтропии также стремится к минимуму
TdSi/dt→ min
Слайд 29В линейной области система эволюционирует к стационарному состоянию , характеризуемому
минимальным производством энтропии , совместимым с наложенными граничными условиями.
Слайд 30
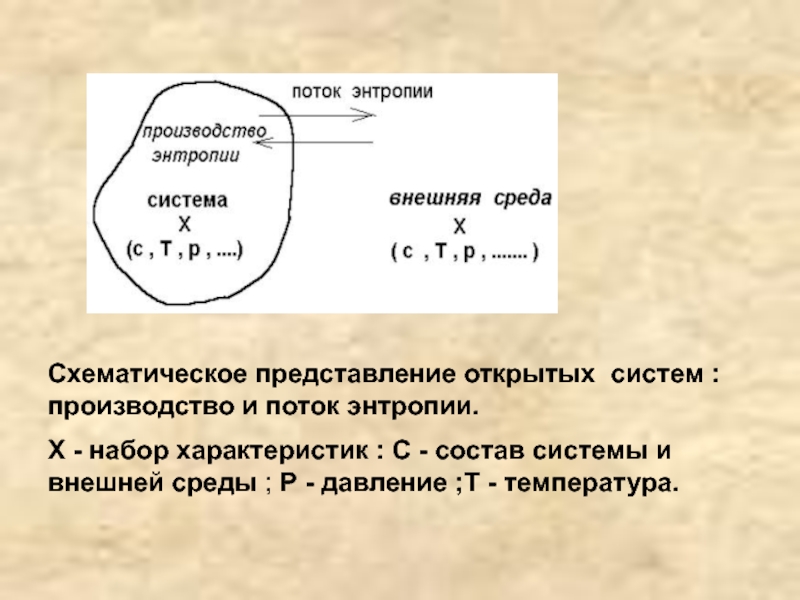
Схематическое представление открытых систем : производство и поток энтропии.
Х -
набор характеристик : С - состав системы и внешней среды ;
Р - давление ;Т - температура.
Слайд 31
Вдали от равновесия фундаментальной величиной для описания эволюции системы является
не производство энтропии, а скорость ее изменения
УНИВЕРСАЛЬНЫЙ КРИТЕРИЙ ЭВОЛЮЦИИ
ОТКРЫТЫХ СИСТЕМ
ТЕОРИЯ ПРИГОЖИНА - ВИАМ
Слайд 32В линейной области система эволюционирует к стационарному состоянию , которое
характеризуется минимальной скоростью производства энтропии , совместимым с наложенными граничными
условиями.
Tσ→min
Слайд 33Критерий эволюции термодинамики линейных необратимых процессов можно использовать для описания
процессов развития, роста и старения организмов.
Если система не находится
в стационарном состоянии, то она будет изменяться до тех пор, пока скорость продукции энтропии, т.е. диссипативная функция (σ), системы не примет наименьшего значения,
Слайд 34σ удельная диссипативная функция
T - абсолютная температура,
V - объем системы,
diS/dt
- скорость продукции энтропии,
Jj - удельные потоки,
Xj -
термодинамические силы,
q - интенсивность теплопродукции.
Термодинамические потоки и силы связаны линейными соотношениями
Слайд 35При использовании критерия скорости производства энтропии для описания возрастных изменений
организмов предполагается, что в процессе этих изменений происходит приближение организмов
к конечному стационарному состоянию, переход живой системы к более вероятному состоянию.
Слайд 36В живых системах удельную диссипативную функцию можно, с известным приближением,
приравнять интенсивности теплопродукции, а следовательно, интенсивности дыхания и гликолиза, которые
в основном определяют теплопродукцию организма.
Тогда в процессе возрастных изменений организмов происходит непрерывное снижение интенсивности этих процессов.
Многочисленные экспериментальные данные хорошо подтверждают это утверждение.
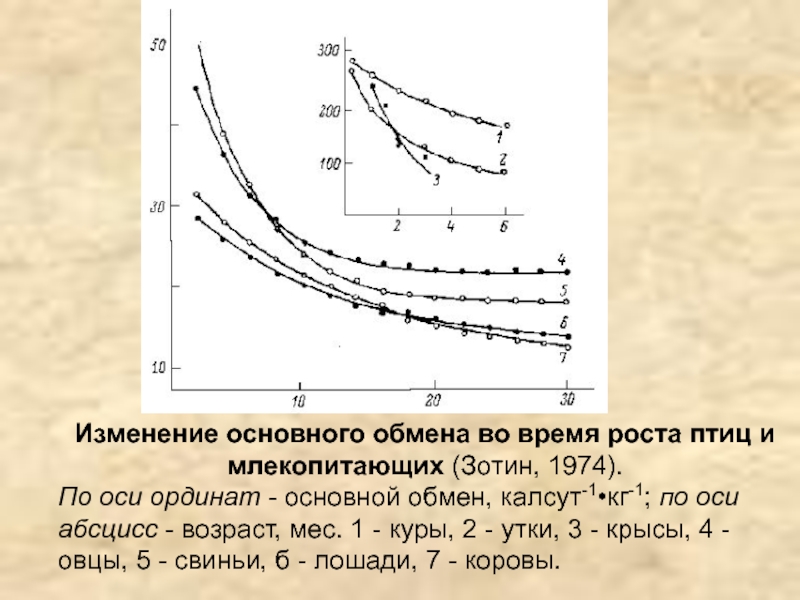
Слайд 37Изменение основного обмена во время роста птиц и млекопитающих (Зотин,
1974).
По оси ординат - основной обмен, калсут-1•кг-1; по оси абсцисс
- возраст, мес. 1 - куры, 2 - утки, 3 - крысы, 4 - овцы, 5 - свиньи, б - лошади, 7 - коровы.
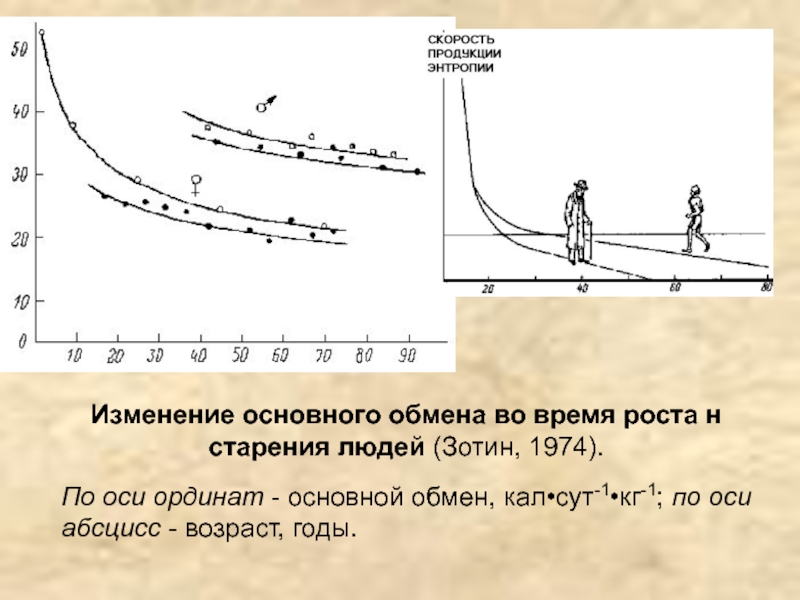
Слайд 38Изменение основного обмена во время роста н старения людей (Зотин,
1974).
По оси ординат - основной обмен, кал•сут-1•кг-1; по оси абсцисс
- возраст, годы.
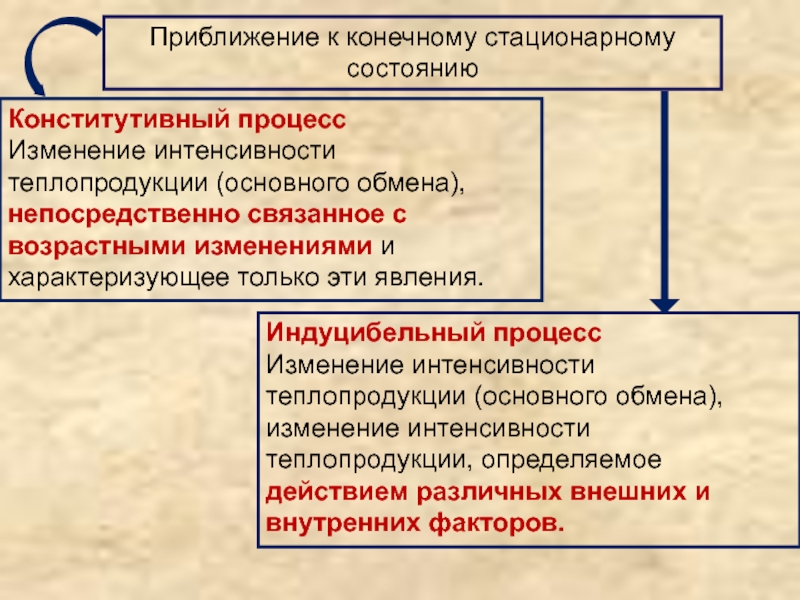
Слайд 39Приближение к конечному стационарному состоянию
Конститутивный процесс
Изменение интенсивности теплопродукции (основного обмена),
непосредственно связанное с возрастными изменениями и характеризующее только эти явления.
Индуцибельный процесс
Изменение интенсивности теплопродукции (основного обмена), изменение интенсивности теплопродукции, определяемое действием различных внешних и внутренних факторов.
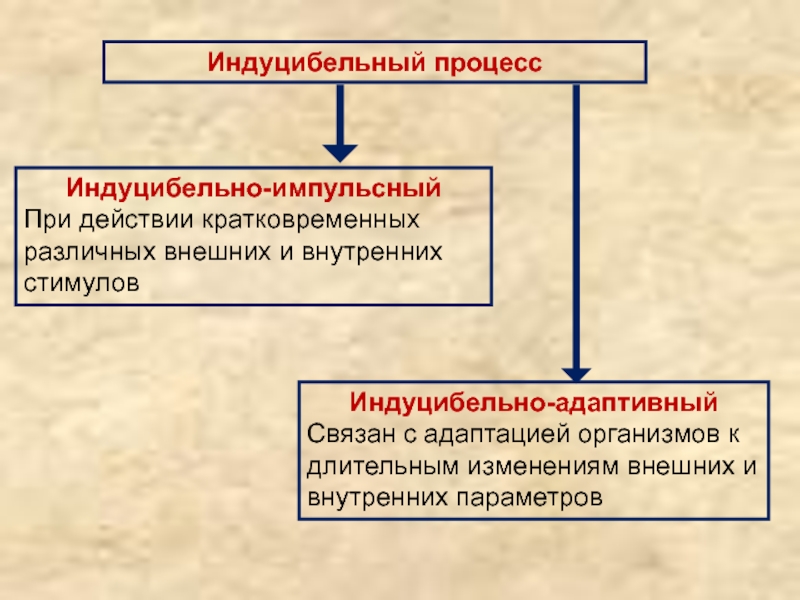
Слайд 40Индуцибельный процесс
Индуцибельно-адаптивный
Связан с адаптацией организмов к длительным изменениям внешних и
внутренних параметров
Индуцибельно-импульсный
При действии кратковременных различных внешних и внутренних стимулов
Слайд 41Шарик катится вниз по наклонному желобу.
Движение шарика по дну
желоба (а, г) соответствует конститутивному приближению организмов к конечному стационарному
состоянию, уклонение и возвращение шарика к текущему стационарному состоянию (б, в) - индуцибильному процессу.
Слайд 42
Возрастные изменения организмов сопровождаются приближением системы к конечному стационарному состоянию,
т. е. непрерывным старением живой системы
Отличие эмбрионального периода и роста
от того периода, который мы обычно называем старением, заключается только в скорости процесса старения.
В онтогенезе должен быть такой период, когда живая система не приближается, а уклоняется от стационарного состояния - процесс, сопровождающийся увеличением величины диссипативной функции системы. (На схеме это соответствует движению шарика вверх по желобу)
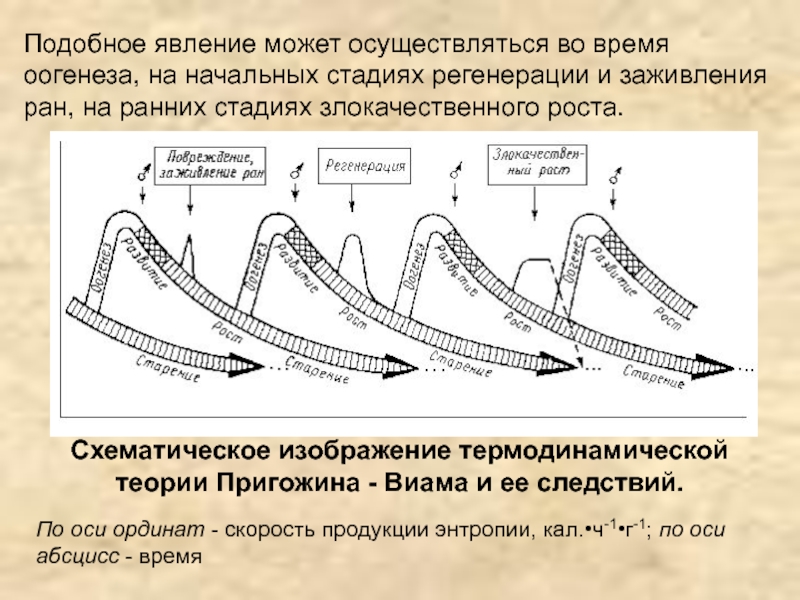
Слайд 43Подобное явление может осуществляться во время оогенеза, на начальных стадиях
регенерации и заживления ран, на ранних стадиях злокачественного роста.
Схематическое
изображение термодинамической теории Пригожина - Виама и ее следствий.
Пo оси ординат - скорость продукции энтропии, кал.•ч-1•г-1; по оси абсцисс - время