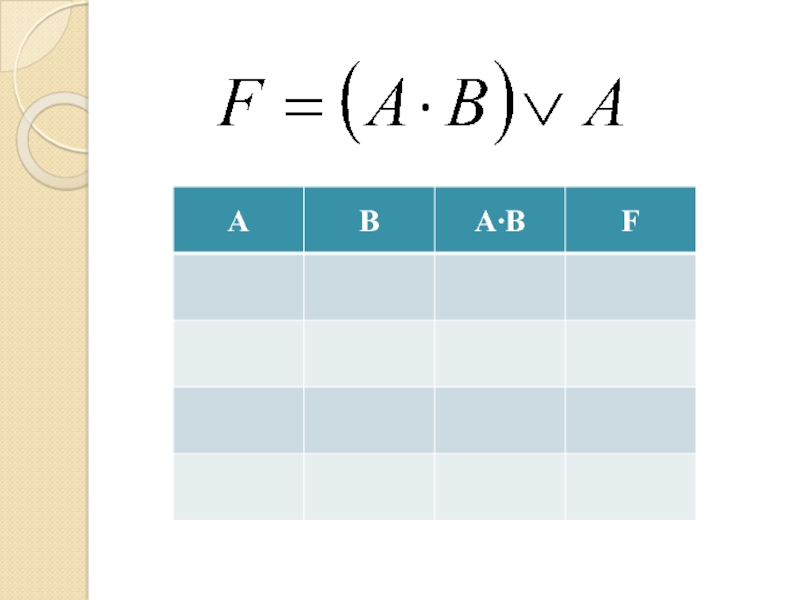Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логические элементы
Содержание
- 1. Логические элементы
- 2. Логикаупорядоченная система мышления, которая создает взаимосвязи между
- 3. АристотельДревнегреческий философОсновоположник логикиИсследовал различные формы рассуждений , ввел понятие силлогизма384 — 322 до н. э.
- 4. Рене Декарт1596 1650Французский философ, математик, механик, физик и физиологРекомендовал в логике использовать математические методы
- 5. Готфрид Вильгельм Лейбниц1646 1716Немецкий философ, логик, математик, механик, физик, юрист,
- 6. Джордж Буль1815 1864Английский математик и логикОсновоположник математической логики«Математический анализ логики» 1847
- 7. Математическая логикаматематизированная ветвь формальной логики «Логика по предмету, математика по методу» И.Н. Бродский
- 8. Пауль Эренфест1880 1933 Австрийский и нидерландский физик-теоретик Член Нидерландской королевской АН, член-корреспондент АН СССР, иностранный член Датской АН
- 9. Михаил Гаврилов1903 1979Советский учёный, стоявший у истоков отечественных информатики и кибернетикиСоздал теорию релейно-контактных схем
- 10. Логический элемент (вентиль)электрическая схема, выполняющая какую-либо логическую
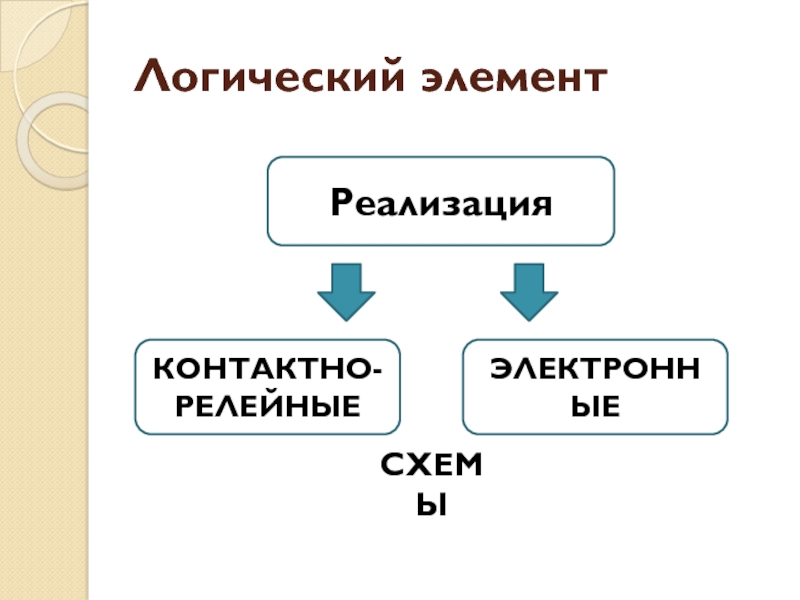
- 11. Логический элементРеализацияКОНТАКТНО-РЕЛЕЙНЫЕЭЛЕКТРОННЫЕСХЕМЫ
- 12. Логический элементэлектрическая схема, выполняющая какую-либо логическую операцию
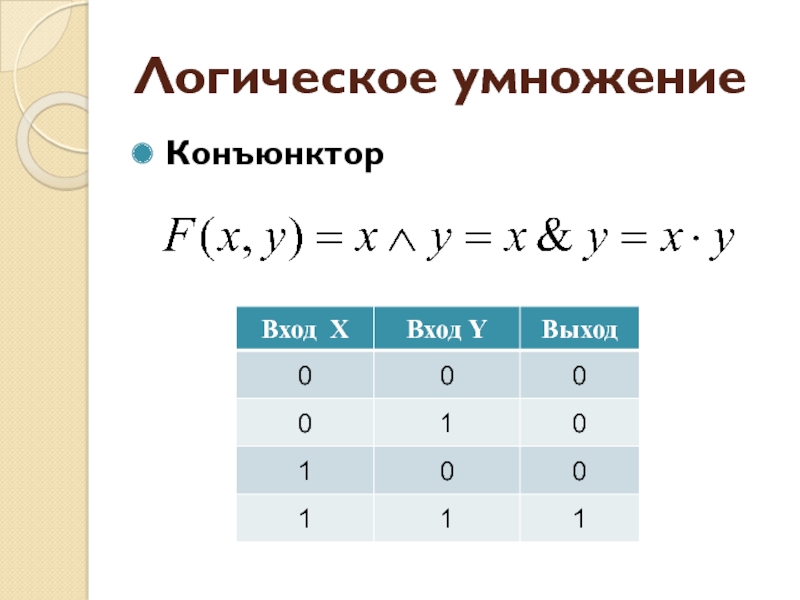
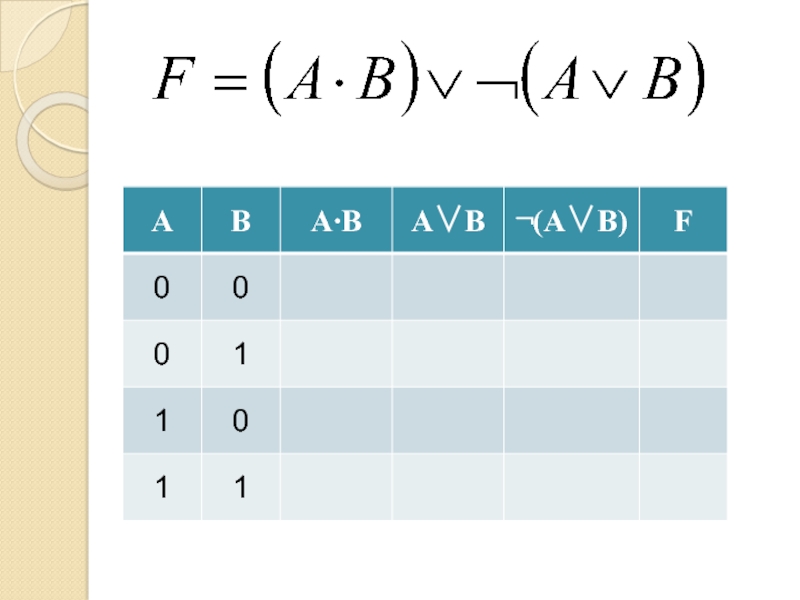
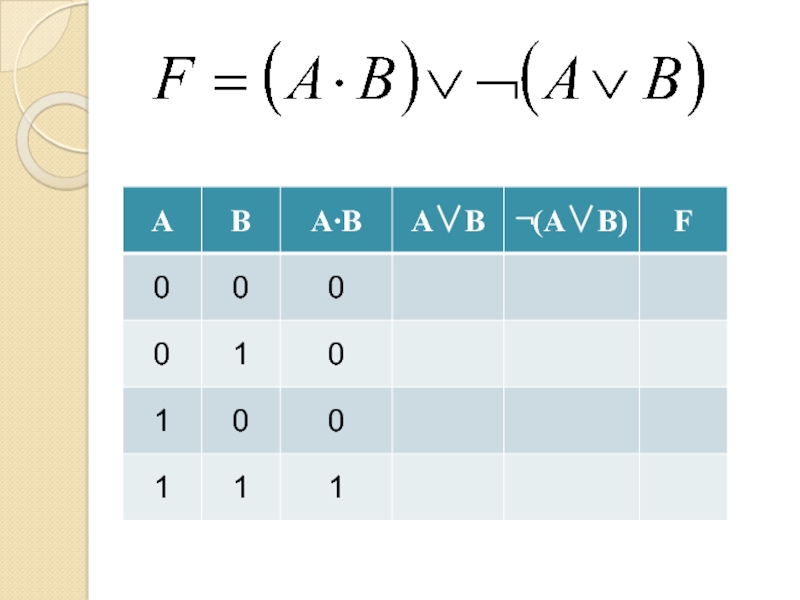
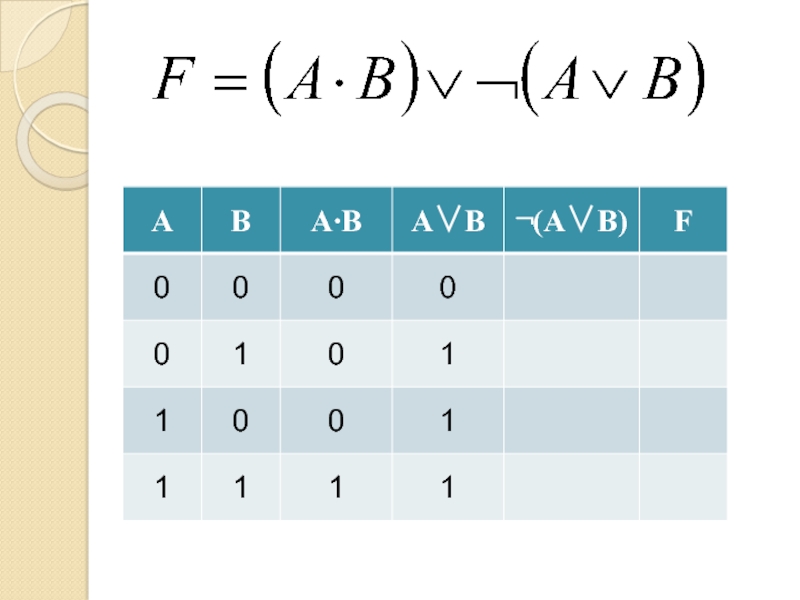
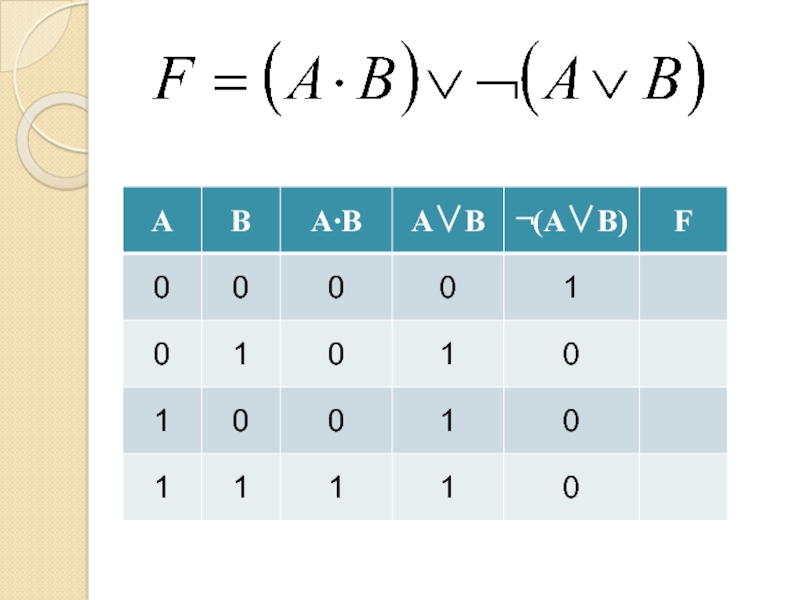
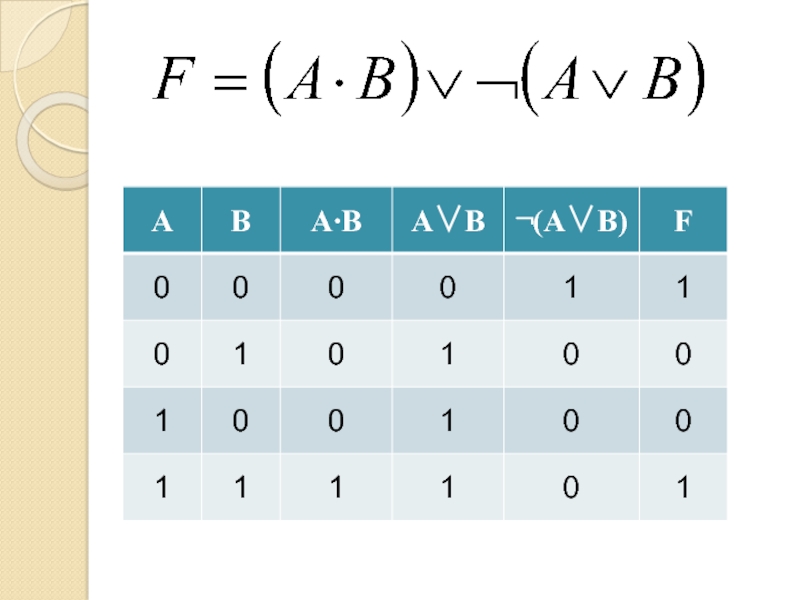
- 13. Логическая операция (функция)Истинностные значенияИстина 1Ложь
- 14. Логический элементВходные данные в виде высокого
- 15. Положительная логикаВысокий уровень (замкнутый ключ, светящийся индикатор)=
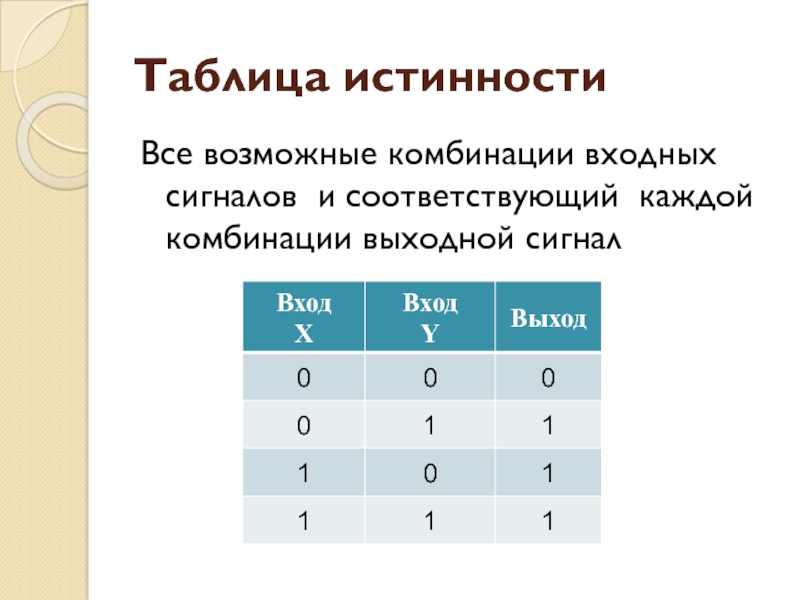
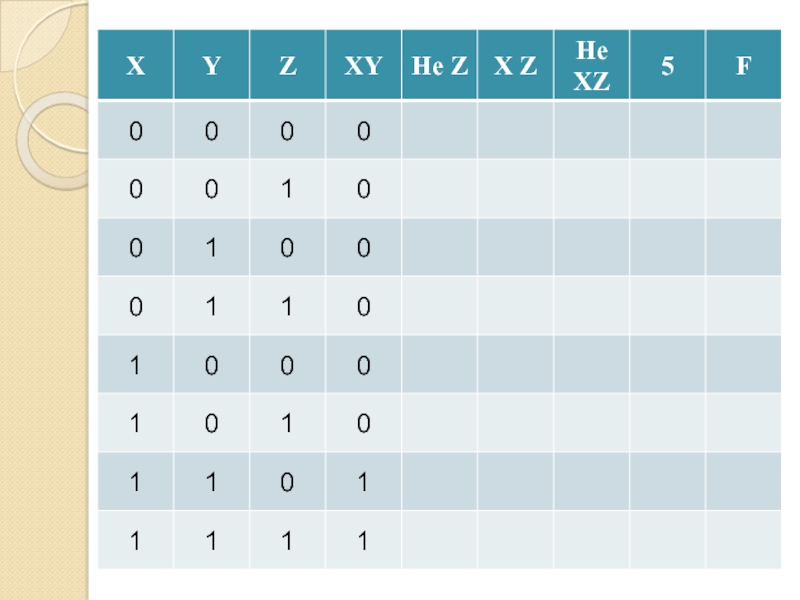
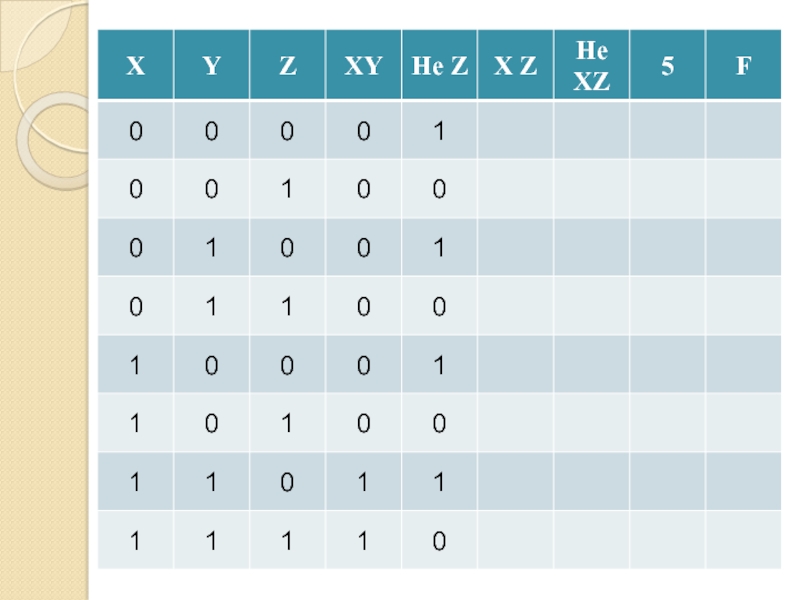
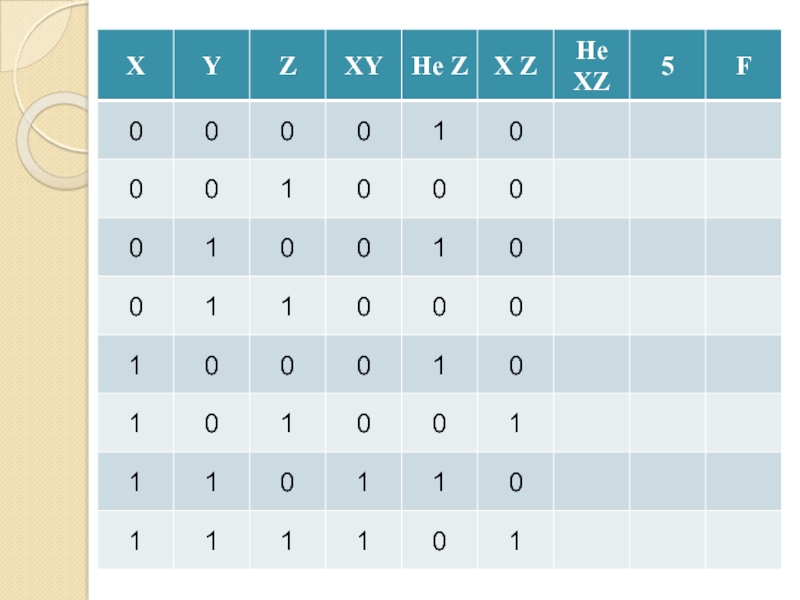
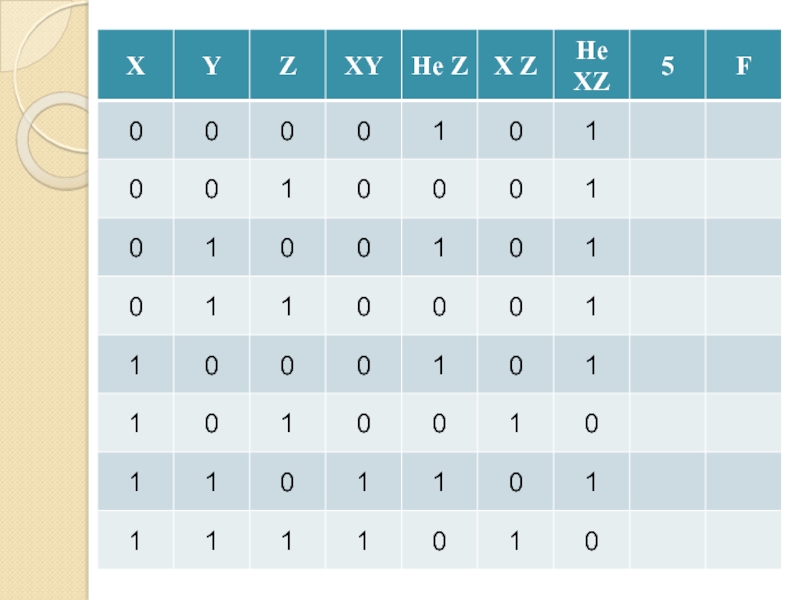
- 16. Таблица истинностиВсе возможные комбинации входных сигналов и соответствующий каждой комбинации выходной сигнал
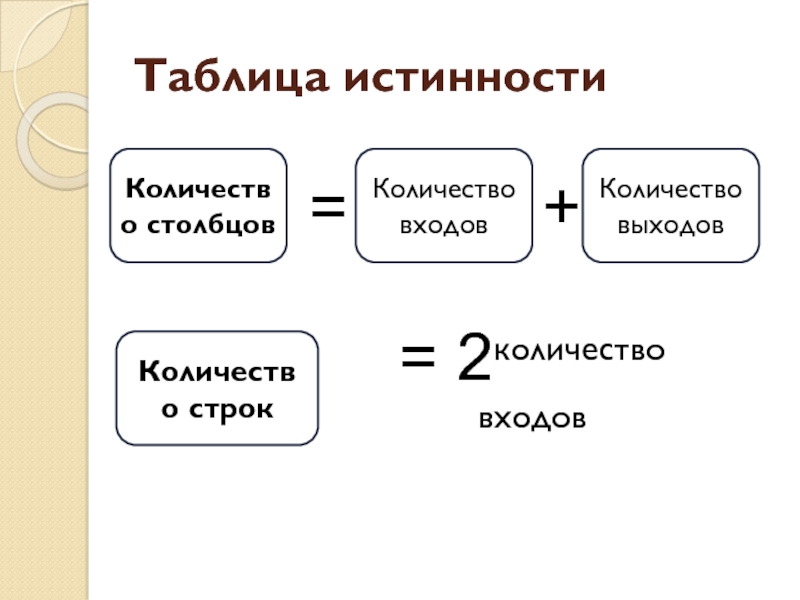
- 17. Таблица истинностиКоличество столбцовКоличество входов=+Количество строк= 2количество входовКоличество выходов
- 18. Логические элементыНЕ инвертированиеИ логическое умножение ИЛИ логическое сложение
- 19. Инверторизменяет значение входного сигнала на прямо противоположное значение
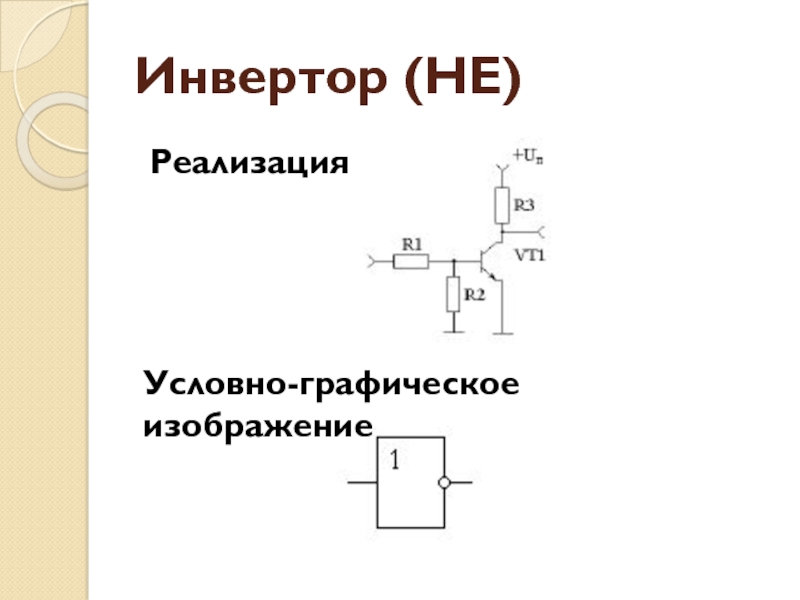
- 20. Инвертор (НЕ)РеализацияУсловно-графическое изображение
- 21. Логическое умножениеКонъюнктор
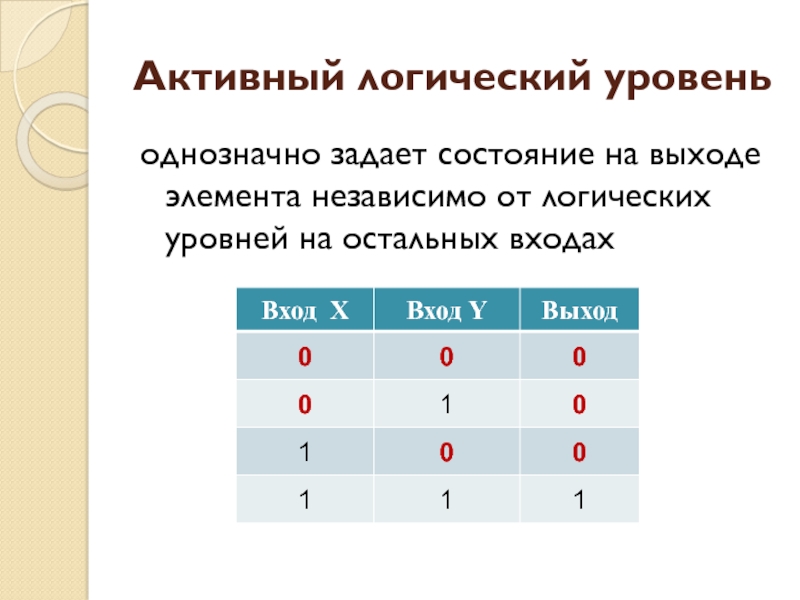
- 22. Активный логический уровеньоднозначно задает состояние на выходе элемента независимо от логических уровней на остальных входах
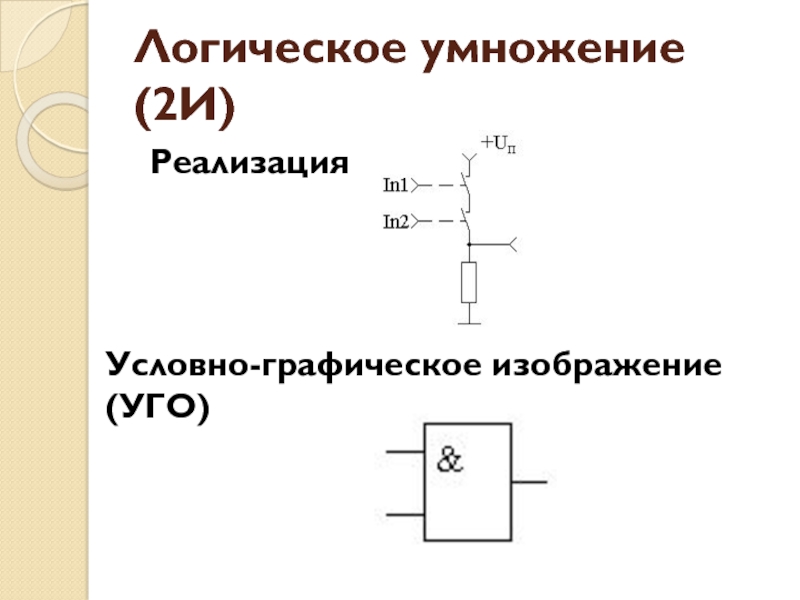
- 23. Логическое умножение (2И)РеализацияУсловно-графическое изображение (УГО)
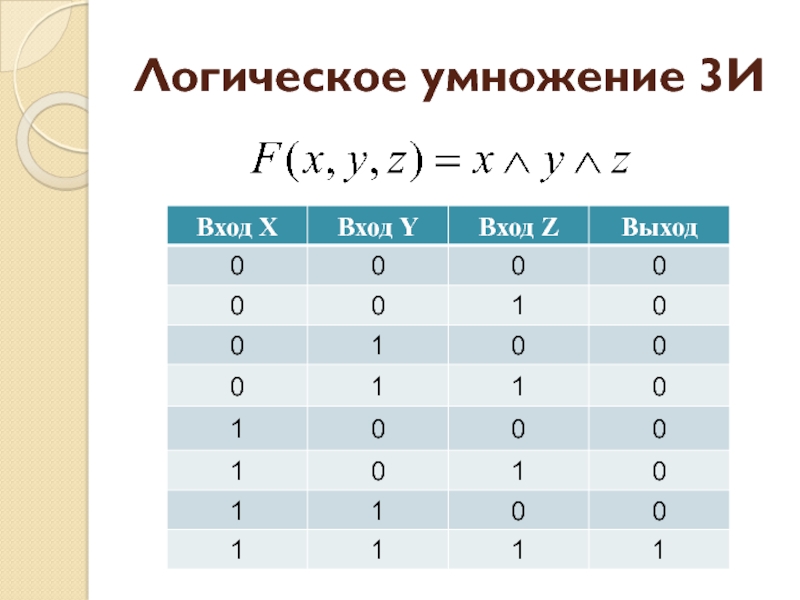
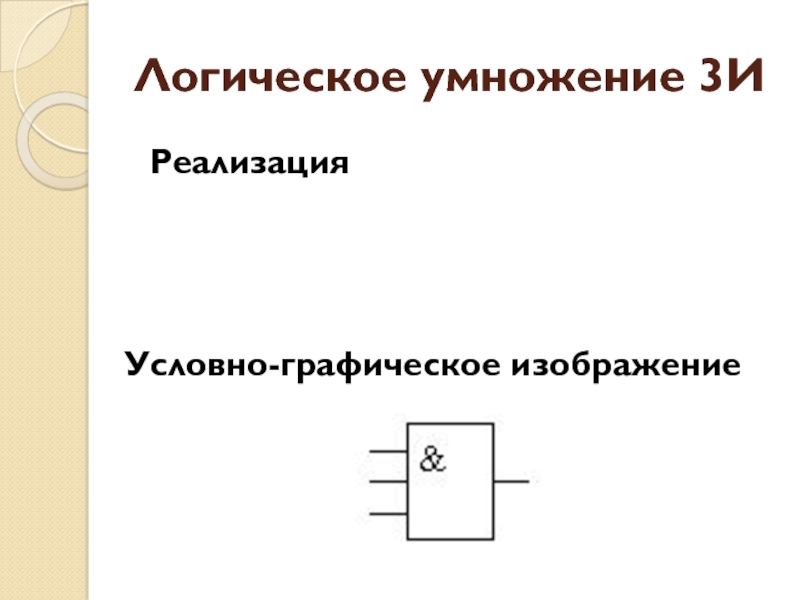
- 24. Логическое умножение 3И
- 25. Логическое умножение 3ИРеализацияУсловно-графическое изображение
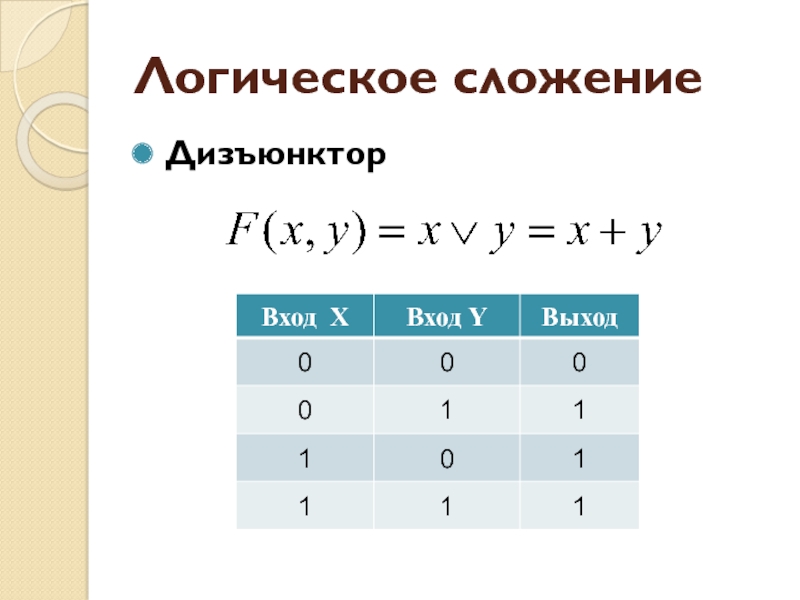
- 26. Логическое сложениеДизъюнктор
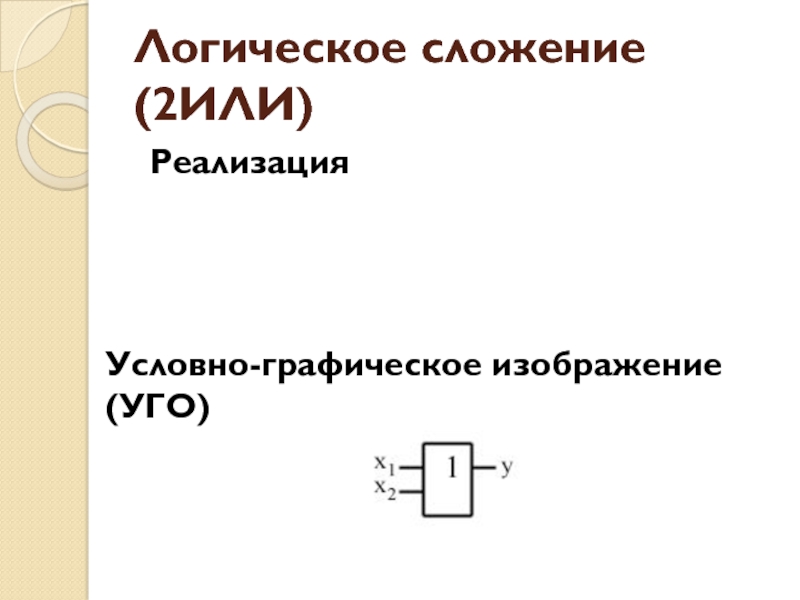
- 27. Логическое сложение (2ИЛИ)РеализацияУсловно-графическое изображение (УГО)
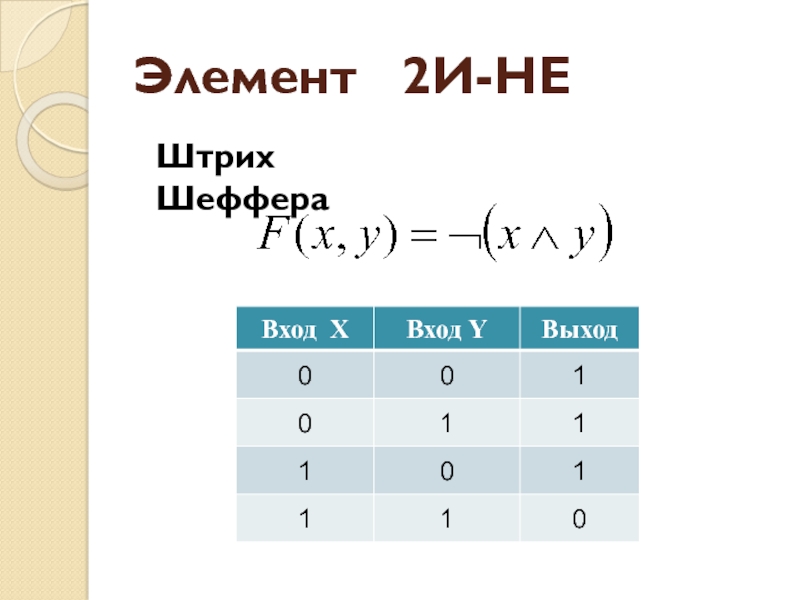
- 28. Элемент 2И-НЕ Штрих Шеффера
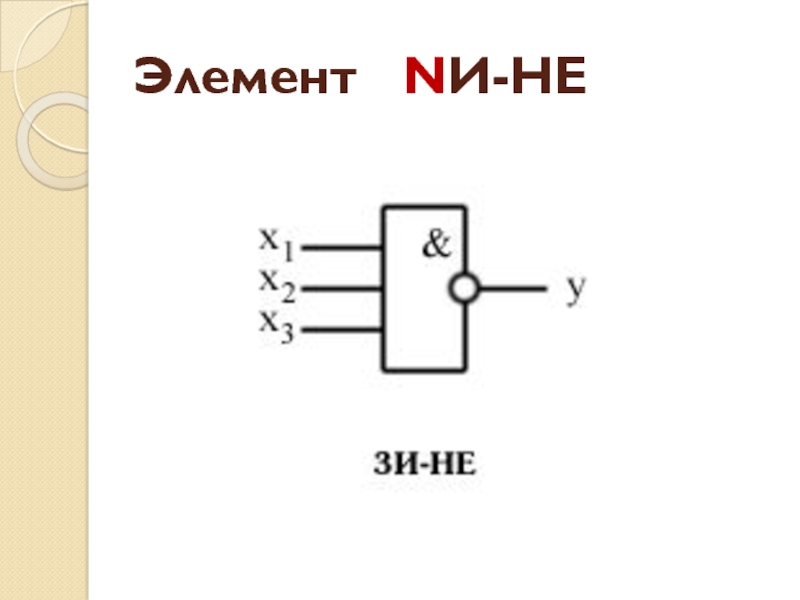
- 29. Элемент NИ-НЕ
- 30. Элемент 2ИЛИ-НЕ Стрелка Пирса
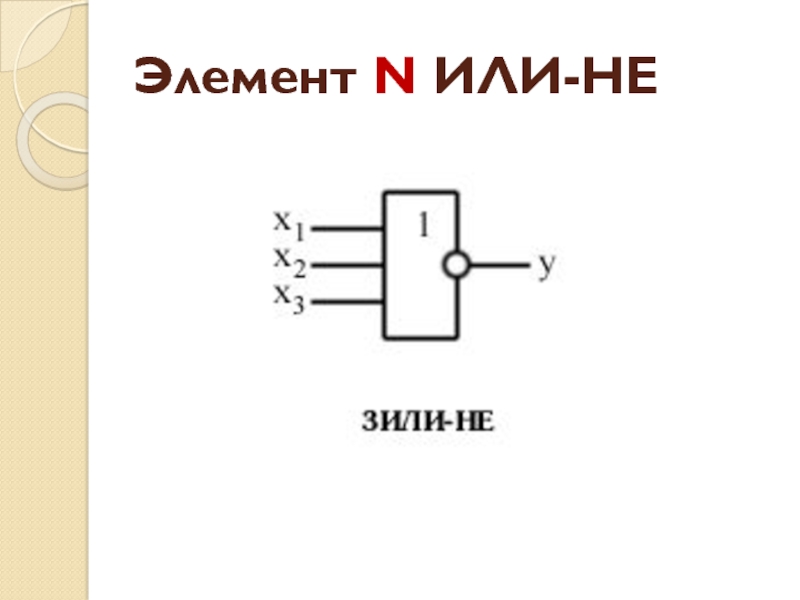
- 31. Элемент N ИЛИ-НЕ
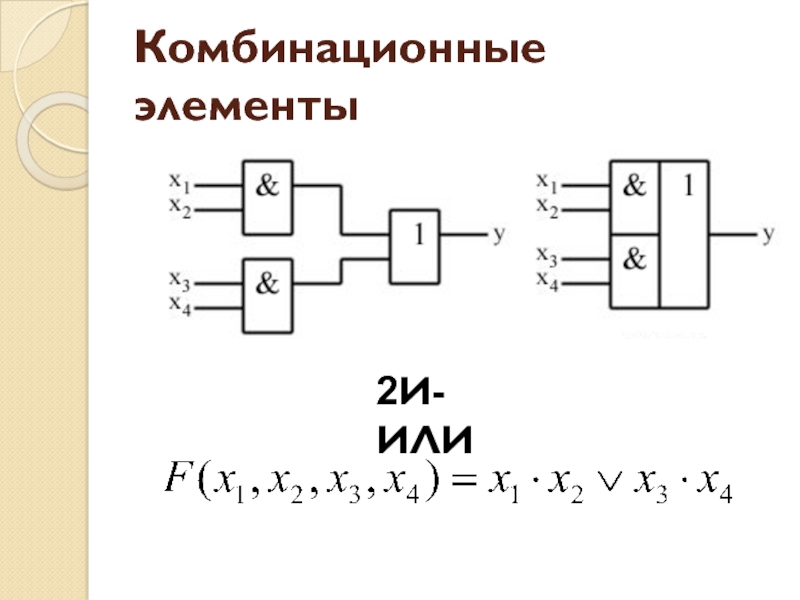
- 32. Комбинационные элементы2И-ИЛИ
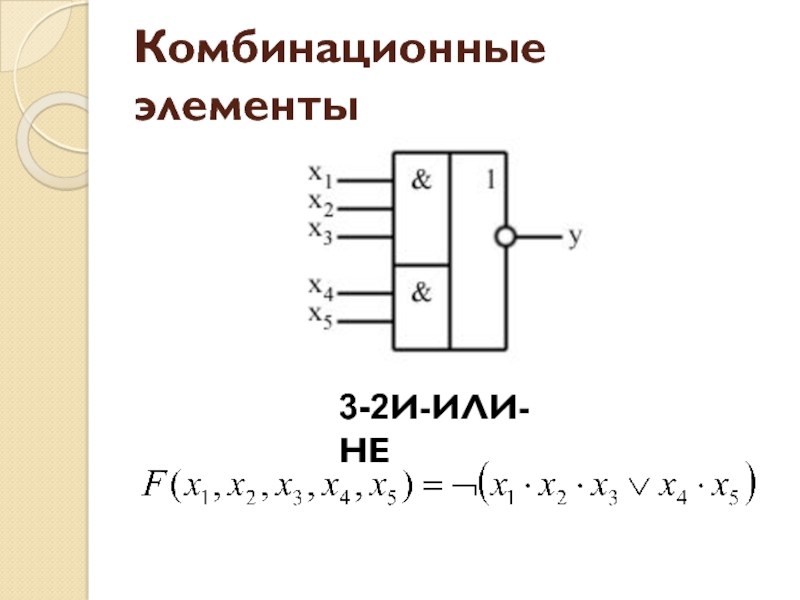
- 33. Комбинационные элементы3-2И-ИЛИ-НЕ
- 34. Функционально полная системаСистема простых логических функций, на основе которой можно получить любую логическую функцию
- 35. Функционально полные системы2И, 2ИЛИ, НЕ2И, НЕ2ИЛИ, НЕ2И–НЕ2ИЛИ–НЕ
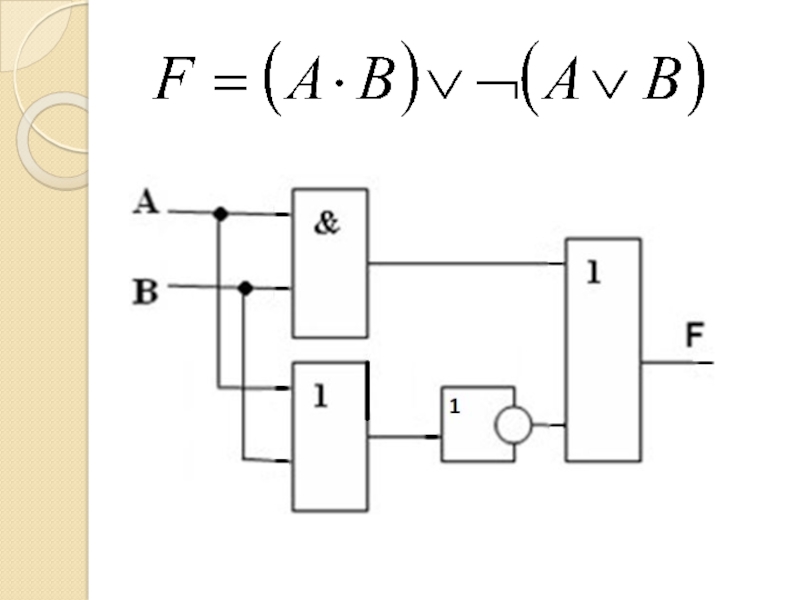
- 36. Реализация цифровых устройств по заданным формулам
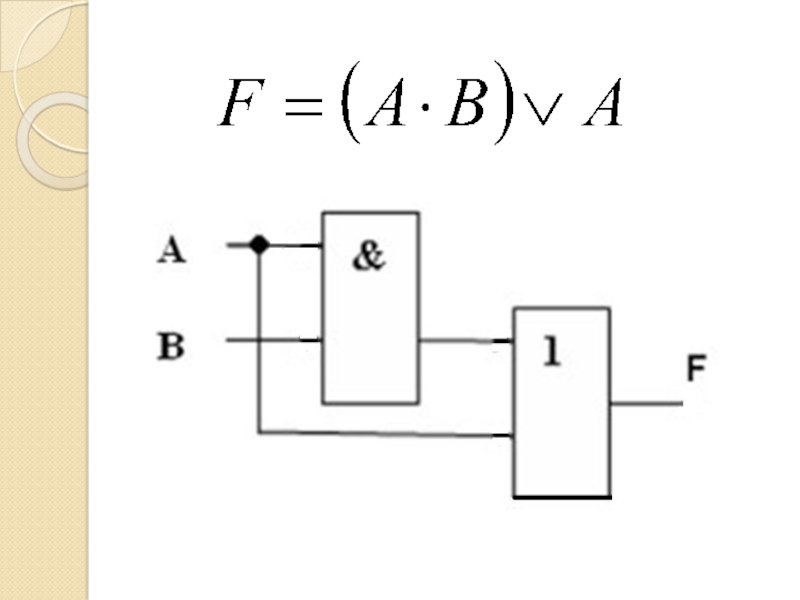
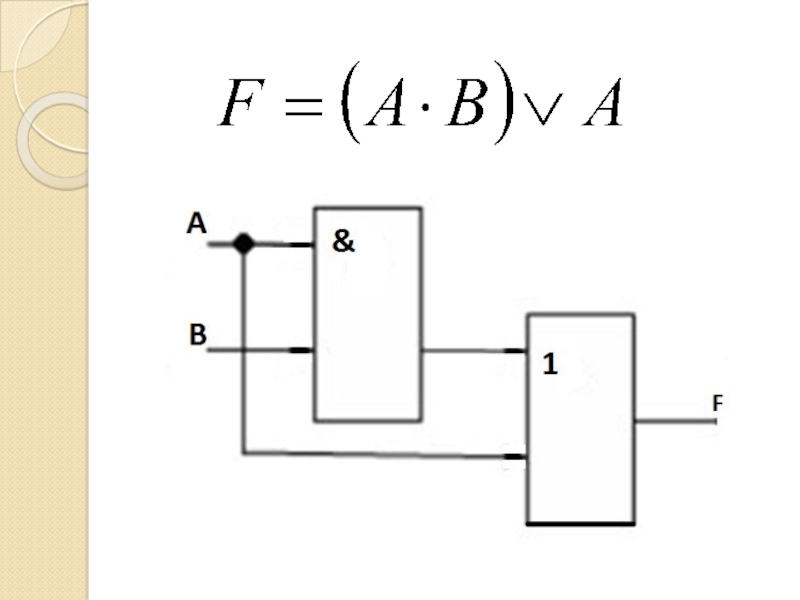
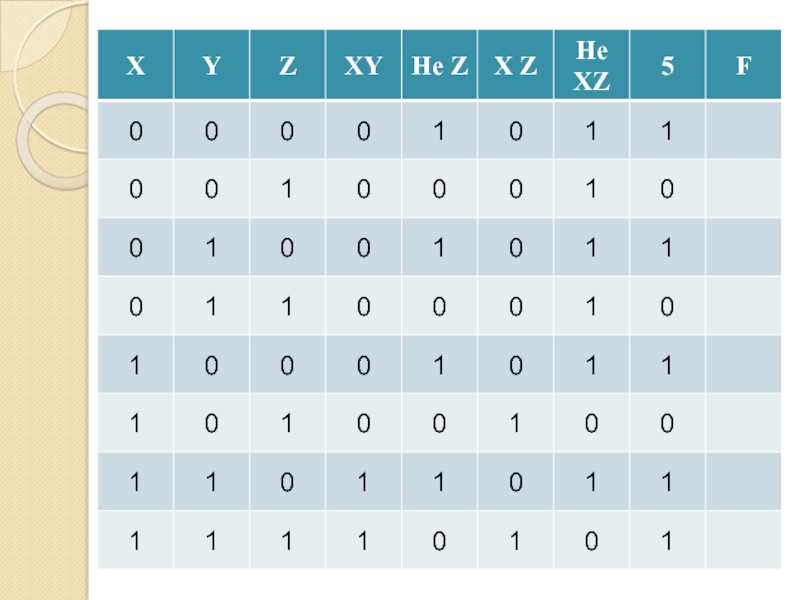
- 37. Слайд 37
- 38. Построение таблиц истинности1.Определяем количество входов2. Количество строк
- 39. Слайд 39
- 40. Слайд 40
- 41. Слайд 41
- 42. Слайд 42
- 43. Слайд 43
- 44. Слайд 44
- 45. Слайд 45
- 46. Слайд 46
- 47. Слайд 47
- 48. Слайд 48
- 49. Слайд 49
- 50. Слайд 50
- 51. Слайд 51
- 52. Слайд 52
- 53. Слайд 53
- 54. Слайд 54
- 55. Слайд 55
- 56. Слайд 56
- 57. Слайд 57
- 58. Слайд 58
- 59. Слайд 59
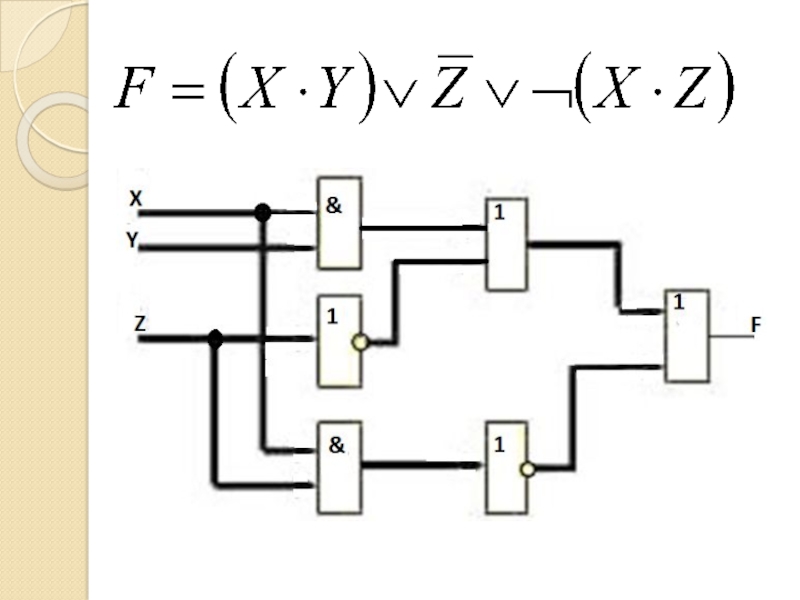
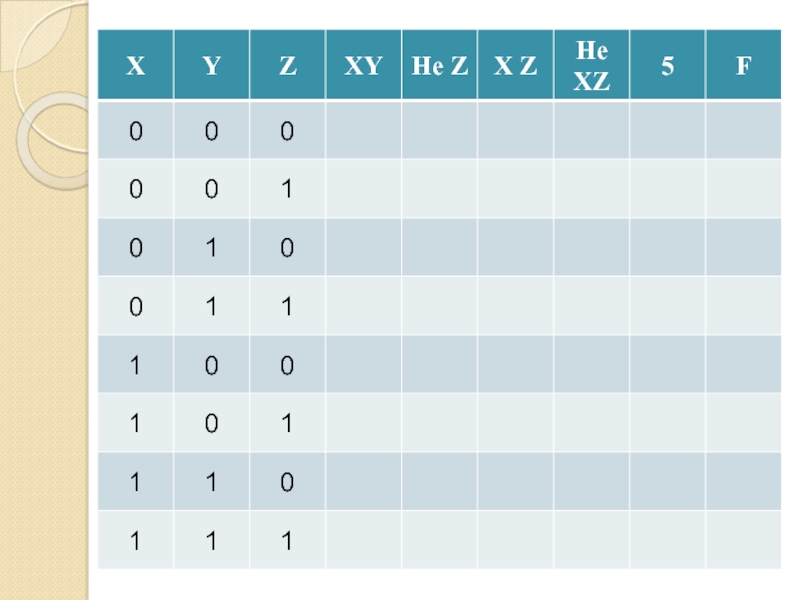
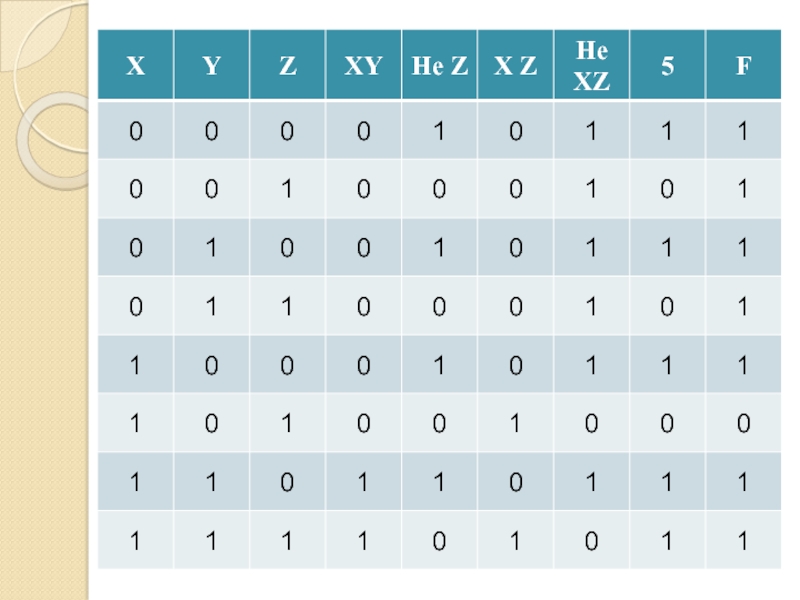
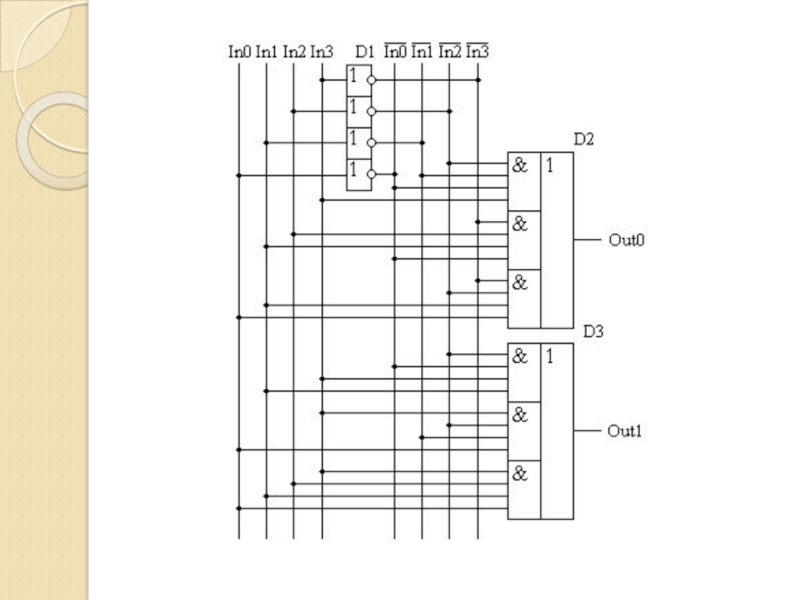
- 60. Реализация цифровых устройств по заданным таблицам истинности
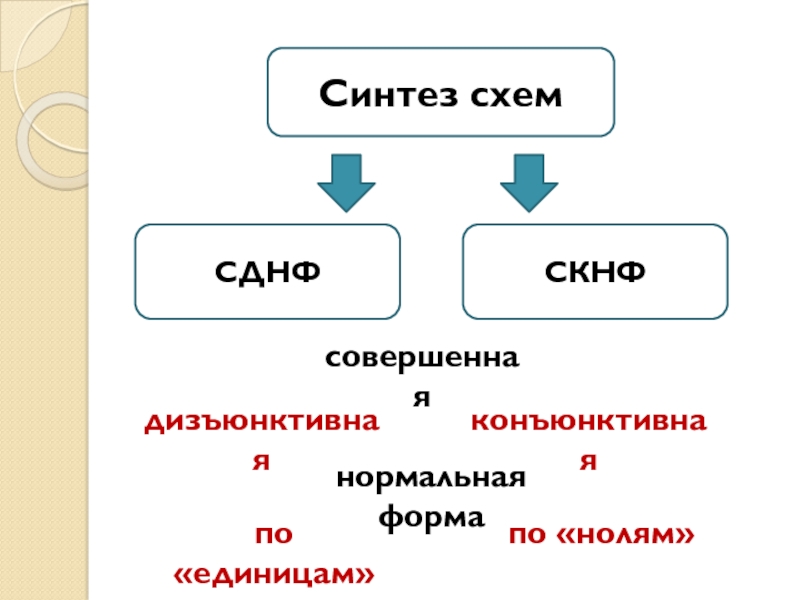
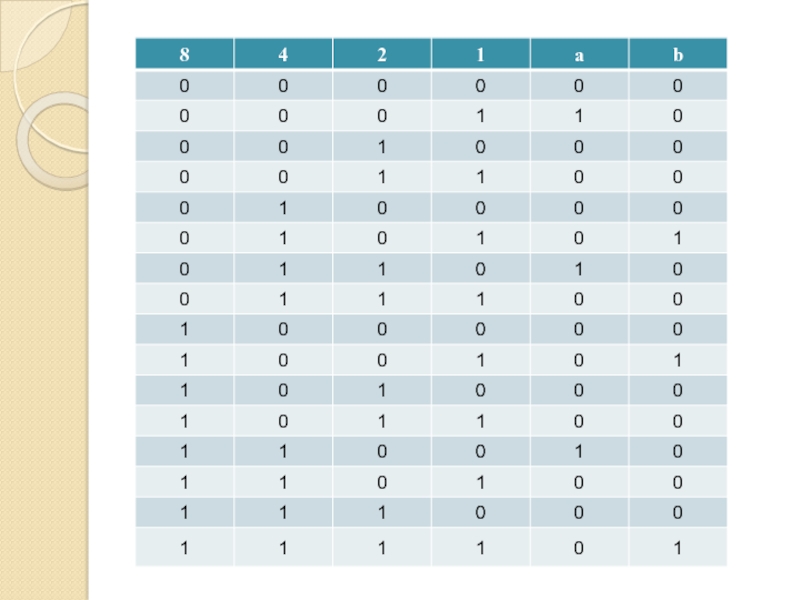
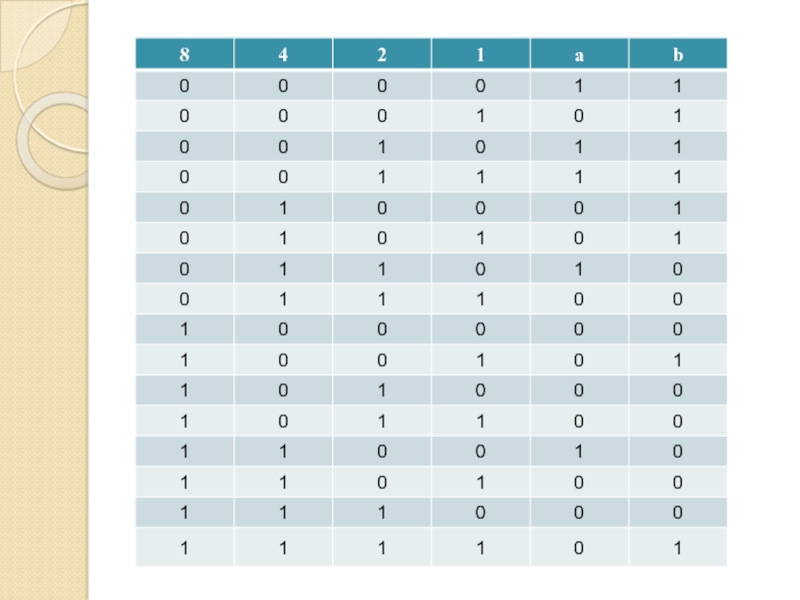
- 61. Синтез схемСДНФСКНФсовершеннаядизъюнктивнаяконъюнктивнаянормальная формапо «единицам»по «нолям»
- 62. Алгоритм (СДНФ)1. Выбираем наборы переменных, при которых
- 63. Алгоритм (СКНФ)1. Выбираем наборы переменных, при которых
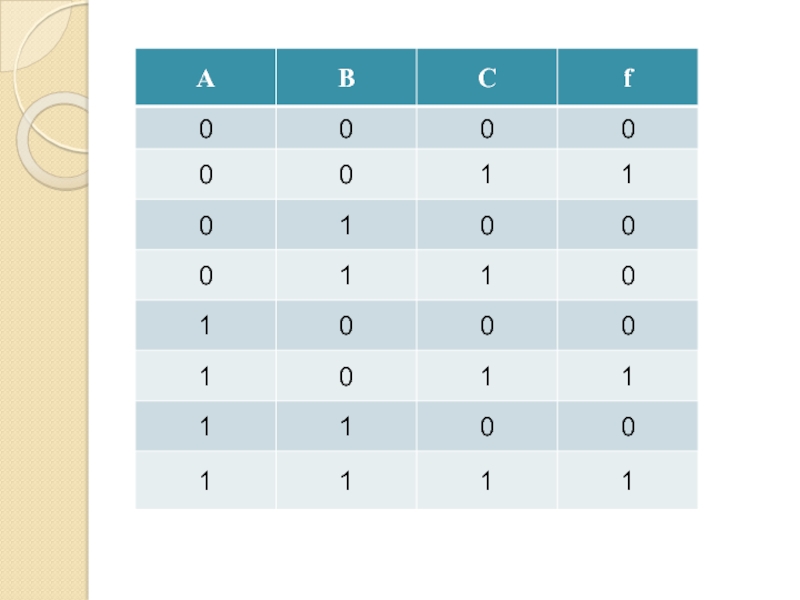
- 64. ЗАДАЧА 1
- 65. Слайд 65
- 66. Слайд 66
- 67. Слайд 67
- 68. Слайд 68
- 69. Формула(А & В & С) (А &
- 70. Формула(А & В & С) (А &
- 71. Формула(А & В & С) (А &
- 72. Слайд 72
- 73. Слайд 73
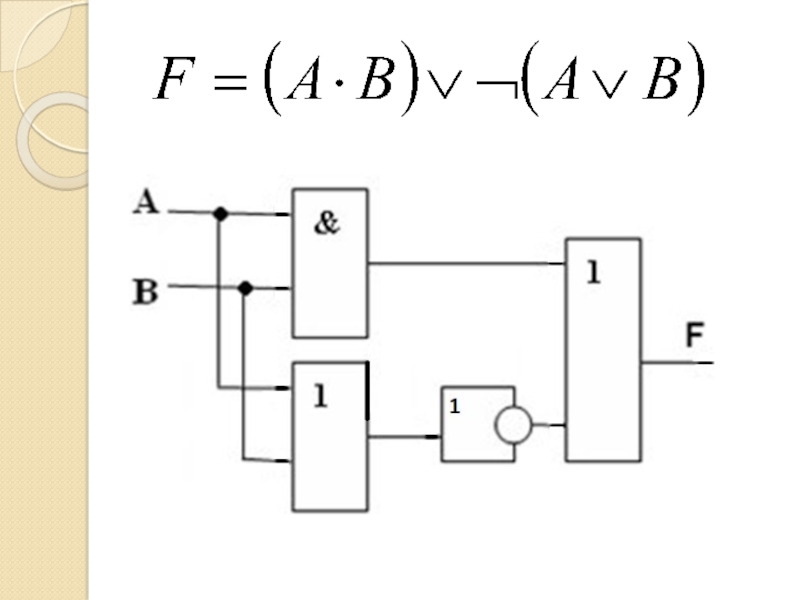
- 74. (А В С) && (А
- 75. (А В С) && (А
- 76. (А В С) && (А
- 77. ЗАДАЧА
- 78. Слайд 78
- 79. Слайд 79
- 80. Слайд 80
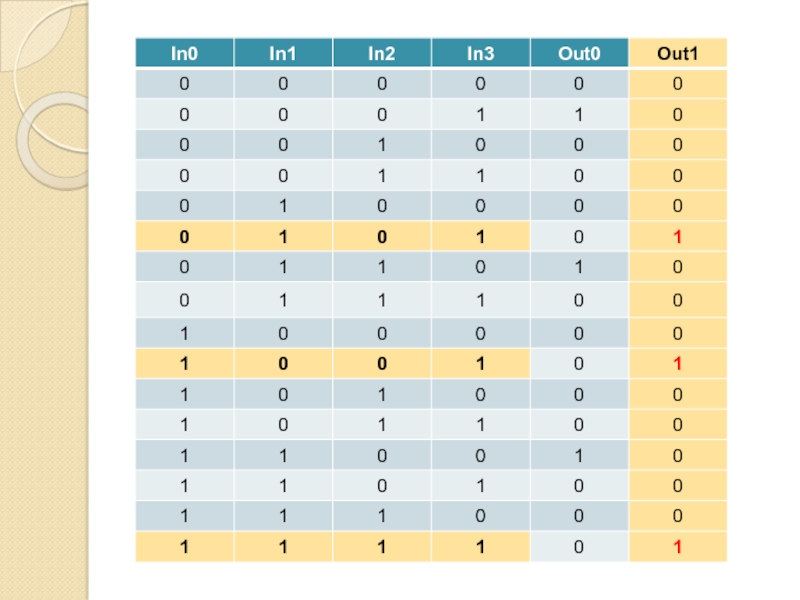
- 81. Формула для Out0(x1∙x2 ∙ x3 ∙ x4)
- 82. Формула для Out0(x1∙x2 ∙ x3 ∙ x4)
- 83. Формула для Out0(x1∙x2 ∙ x3 ∙ x4)
- 84. Слайд 84
- 85. Формула для Out1(x1∙x2 ∙ x3 ∙ x4)
- 86. Слайд 86
- 87. Слайд 87
- 88. Слайд 88
- 89. Скачать презентанцию
Логикаупорядоченная система мышления, которая создает взаимосвязи между заданными условиями и позволяет делать умозаключения, основываясь на предпосылках и предположениях
Слайды и текст этой презентации
Слайд 2Логика
упорядоченная система мышления, которая создает взаимосвязи между заданными условиями и
позволяет делать умозаключения, основываясь на предпосылках и предположениях
Слайд 3Аристотель
Древнегреческий философ
Основоположник логики
Исследовал различные формы рассуждений , ввел понятие силлогизма
384
— 322 до н. э.
Слайд 4Рене Декарт
1596 1650
Французский
философ,
математик, механик, физик и физиолог
Рекомендовал в логике использовать математические
методы
Слайд 5Готфрид Вильгельм Лейбниц
1646 1716
Немецкий философ,
логик, математик,
механик, физик, юрист, историк, дипломат, языковед и
изобретатель
Предложил в логике использовать двоичную систему счисления и математическую символику
Слайд 6Джордж Буль
1815 1864
Английский математик и логик
Основоположник математической логики
«Математический анализ
логики»
1847
Слайд 7Математическая логика
математизированная ветвь формальной логики
«Логика по предмету, математика по методу»
И.Н.
Бродский
Слайд 8Пауль Эренфест
1880 1933
Австрийский и нидерландский физик-теоретик
Член Нидерландской королевской АН,
член-корреспондент
АН СССР,
иностранный член Датской АН
Слайд 9Михаил Гаврилов
1903 1979
Советский учёный, стоявший у истоков отечественных информатики
и кибернетики
Создал теорию релейно-контактных схем
Слайд 10Логический элемент (вентиль)
электрическая схема, выполняющая какую-либо логическую операцию (операции) над
входными данными, заданными в виде уровней напряжения, и возвращающая результат
операции в виде выходного уровня напряженияСлайд 12Логический элемент
электрическая схема, выполняющая какую-либо логическую операцию (операции) над входными
данными, заданными в виде уровней напряжения, и возвращающая результат операции
в виде выходного уровня напряженияСлайд 13Логическая операция (функция)
Истинностные значения
Истина 1
Ложь 0
На входе
набор из 0 и 1
На выходе 0 или 1
Слайд 14Логический элемент
Входные данные в виде высокого и низкого уровней
напряжения на входах
Значения определяются электрическими параметрами схемы и одинаковы как
для входных и для выходных сигналовСлайд 15Положительная логика
Высокий уровень (замкнутый ключ, светящийся индикатор)= Истина = 1
Низкий
уровень (разомкнутый ключ, не светящийся индикатор)= Ложь = 0
Отрицательная логика
наоборотСлайд 16Таблица истинности
Все возможные комбинации входных сигналов и соответствующий каждой комбинации
выходной сигнал
Слайд 17Таблица истинности
Количество столбцов
Количество входов
=
+
Количество строк
= 2количество входов
Количество выходов
Слайд 22Активный логический уровень
однозначно задает состояние на выходе элемента независимо от
логических уровней на остальных входах
Слайд 34Функционально полная система
Система простых логических функций, на основе которой можно
получить любую логическую функцию
Слайд 38Построение таблиц истинности
1.Определяем количество входов
2. Количество строк в таблице
3.Определяем количество
действий
4. Количество столбцов в таблице = количество входов + количество
действий5.Заполняем таблицу
2количество входов
Слайд 61Синтез схем
СДНФ
СКНФ
совершенная
дизъюнктивная
конъюнктивная
нормальная форма
по «единицам»
по «нолям»
Слайд 62Алгоритм (СДНФ)
1. Выбираем наборы переменных, при которых выходное значение равно
1.
2. Для каждого такого набора записываем конъюнкции всех переменных, если
переменная имеет значение 0, берём её в инвертированном виде.3. Полученные конъюнкции объединяем операцией дизъюнкции
Слайд 63Алгоритм (СКНФ)
1. Выбираем наборы переменных, при которых выходное значение равно
0.
2. Для каждого такого набора записываем дизъюнкции всех переменных, если
переменная имеет значение 1, берём её в инвертированном виде.3. Полученные дизъюнкции объединяем операцией конъюнкции
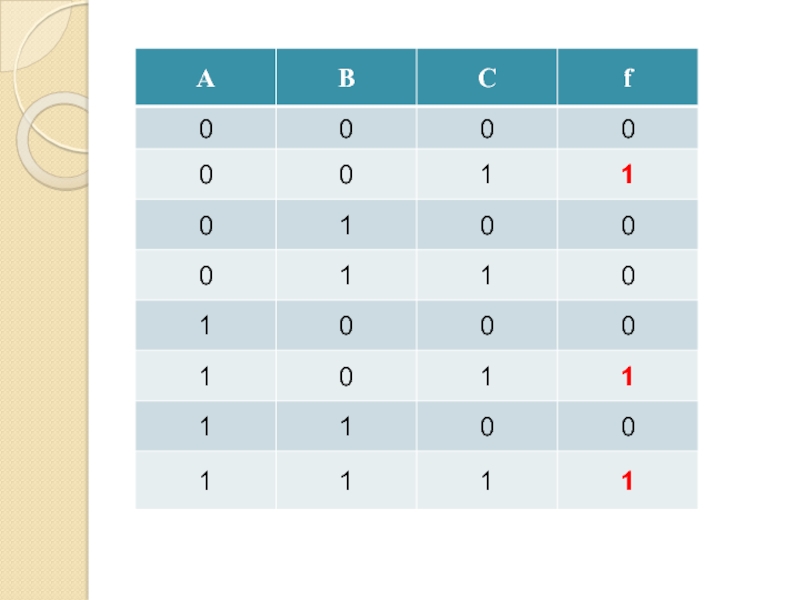
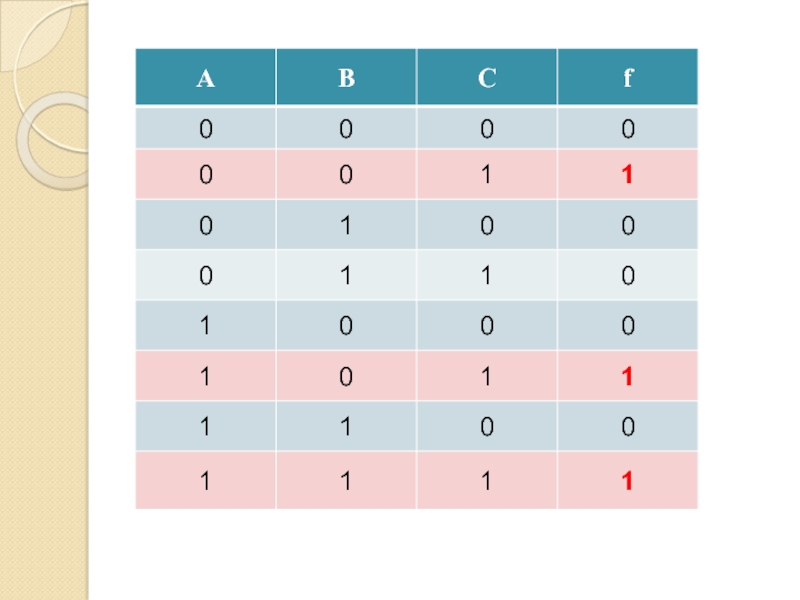
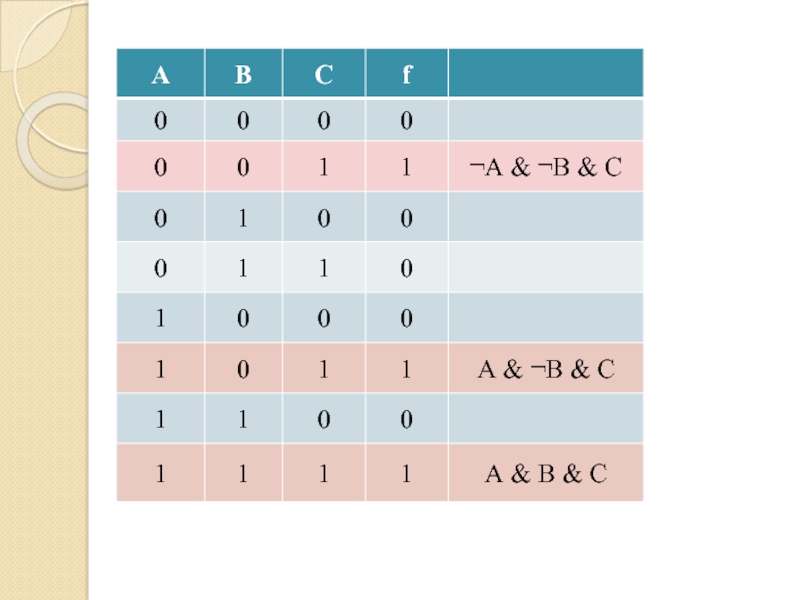
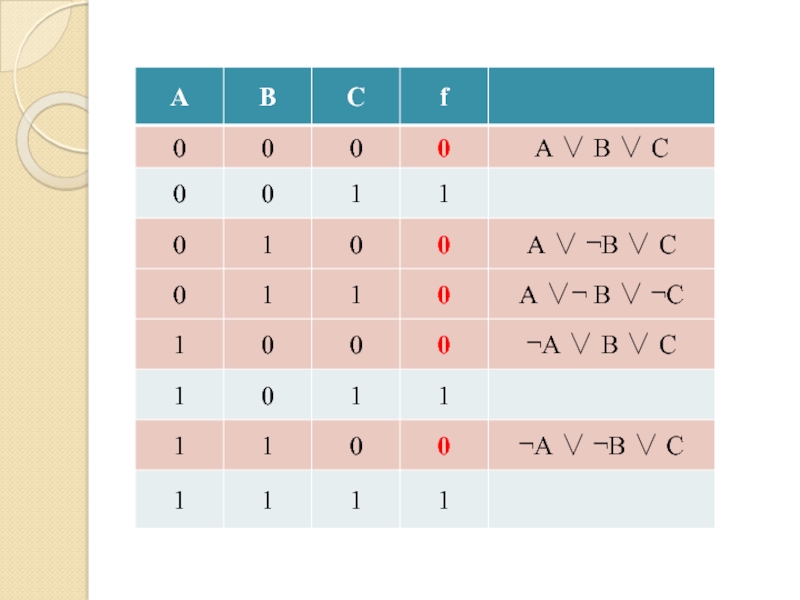
Слайд 69Формула
(А & В & С)
(А & В & С)
(А & В & С)
Совершенная дизъюнктивная нормальная форма (СДНФ)
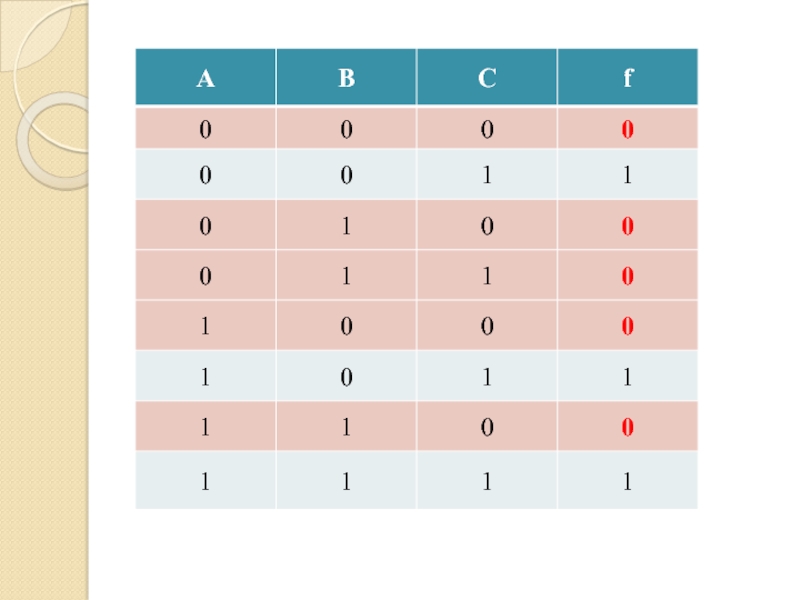
Слайд 74(А В С) &
& (А В
С) &
& (А В С) &
& (А
В С) && (А В С)
Совершенная конъюнктивная нормальная форма (СКНФ)
Слайд 75(А В С) &
& (А В
С) &
& (А В С) &
& (А
В С) && (А В С)
Совершенная конъюнктивная нормальная форма
Слайд 76(А В С) &
& (А В
С) &
& (А В С) &
& (А
В С) && (А В С)
Совершенная конъюнктивная нормальная форма
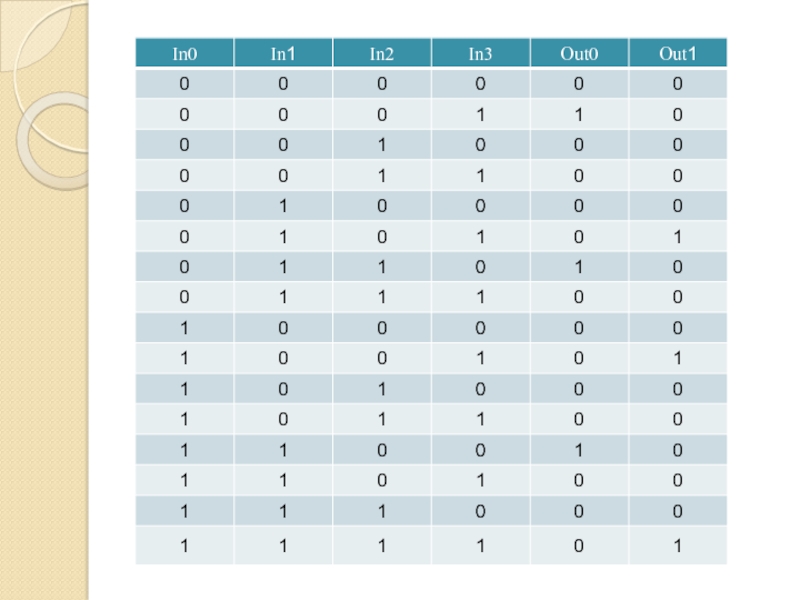
Слайд 81Формула для Out0
(x1∙x2 ∙ x3 ∙ x4)
(x1 ∙ x2
∙ x3 ∙ x4)
(x1 ∙ x2 ∙
x3 ∙ x4)Совершенная дизъюнктивная нормальная форма (СДНФ)
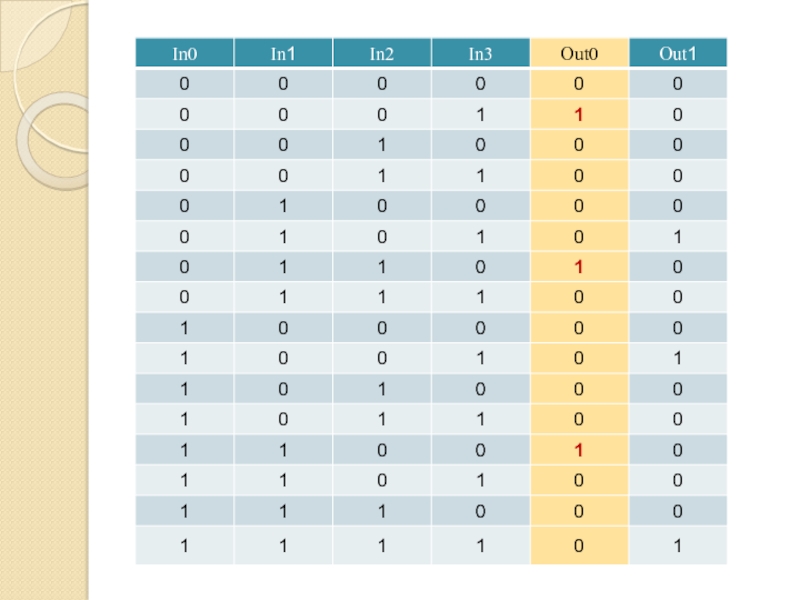
Слайд 82Формула для Out0
(x1∙x2 ∙ x3 ∙ x4)
(x1 ∙ x2
∙ x3 ∙ x4)
(x1 ∙ x2 ∙
x3 ∙ x4)Совершенная дизъюнктивная нормальная форма (СДНФ)
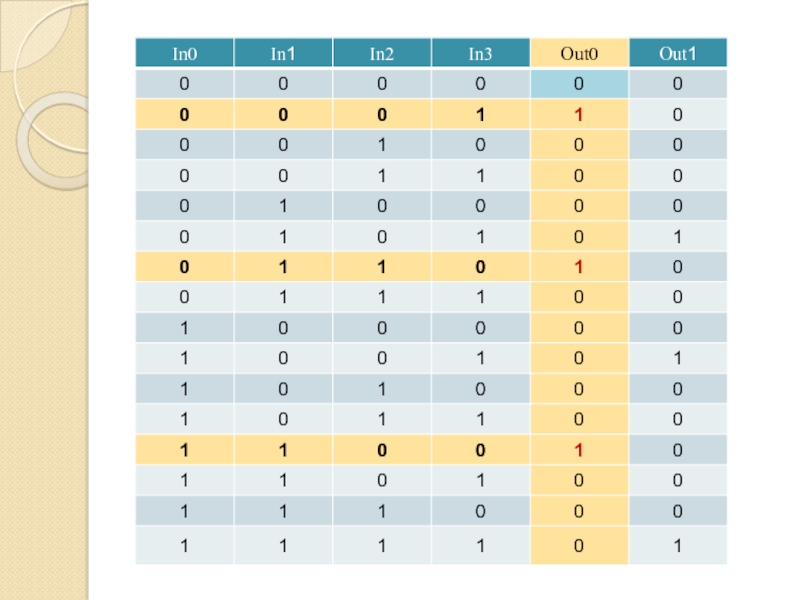
Слайд 83Формула для Out0
(x1∙x2 ∙ x3 ∙ x4)
(x1 ∙ x2
∙ x3 ∙ x4)
(x1 ∙ x2 ∙
x3 ∙ x4)Совершенная дизъюнктивная нормальная форма (СДНФ)
Слайд 85Формула для Out1
(x1∙x2 ∙ x3 ∙ x4)
(x1 ∙
x2 ∙ x3 ∙ x4)
(x1 ∙ x2 ∙
x3 ∙ x4)Совершенная дизъюнктивная нормальная форма (СДНФ)