Слайд 2Основные определения математической логики
Высказыванием называется утверждение, о котором можно определенно
сказать, истинно оно или ложно. Высказываний одновременно истинных и ложных
не бывает.
Высказывания бывают простыми и сложными. Простые отдельные высказывания - это логические переменные, их принято обозначать буквами латинского алфавита. Например, если простое высказывание X истинно, то X = 1, если же ложно, то X = 0.
Логическая (булева) переменная - эта такая величина x, которая может принимать только два значения: «Истина» или «Ложь».
Функция f(x1, x2, ..., xn) называется логической (переключательной), или булевой, если она, так же как и ее аргументы xi, может принимать только два значения: «Истина» или «Ложь».
Слайд 3Логические функции могут быть описаны различными способами:
в виде таблицы истинности;
совершенными
нормальными формами:
в виде формулы.
Таблица истинности указывает значение логической функции при
всех значения наборов аргументов
Слайд 4ПРЕДСТАВЛЕНИЕ ЛОГИЧЕСКОЙ ФУНКЦИИ
В ВИДЕ ТАБЛИЦЫ ИСТИННОСТИ
Таблица истинности указывает значение
логической функции при всех значениях наборов аргументов.
Элементарные логические функции -
это функции, содержащие не более одной логической операции
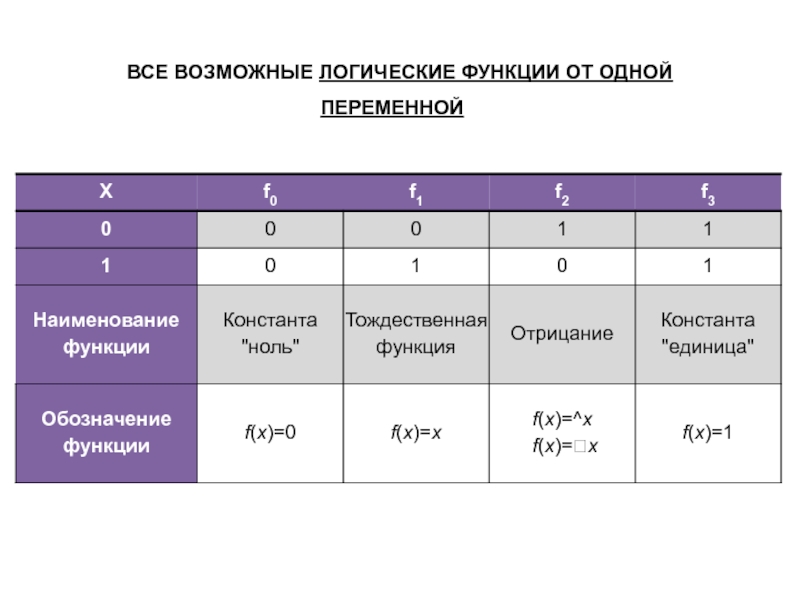
Слайд 5ВСЕ ВОЗМОЖНЫЕ ЛОГИЧЕСКИЕ ФУНКЦИИ ОТ ОДНОЙ ПЕРЕМЕННОЙ
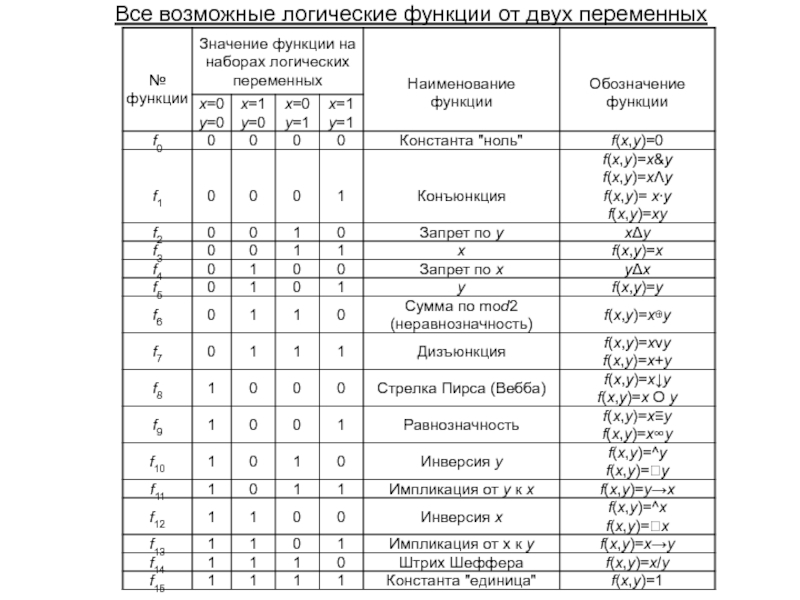
Слайд 6Все возможные логические функции от двух переменных
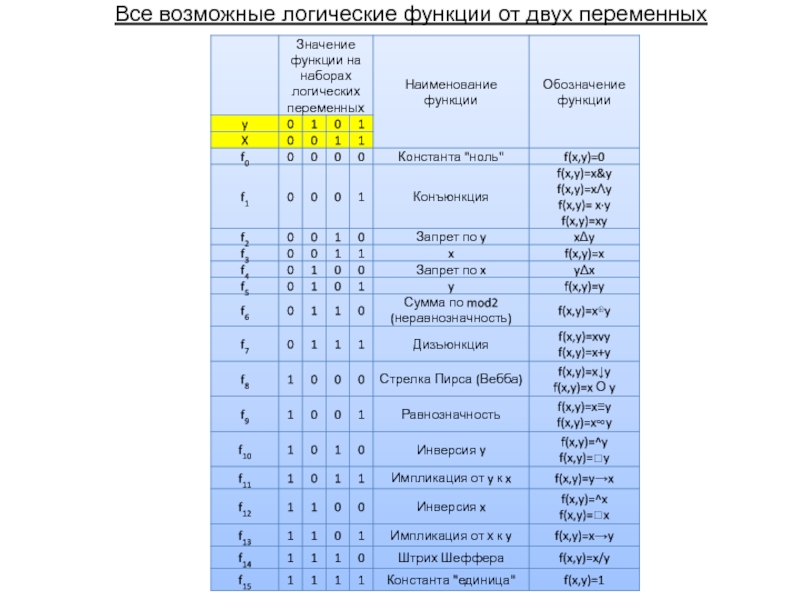
Слайд 7Все возможные логические функции от двух переменных
Слайд 8Все возможные логические функции от двух переменных
Общее количество функций от
n переменных:
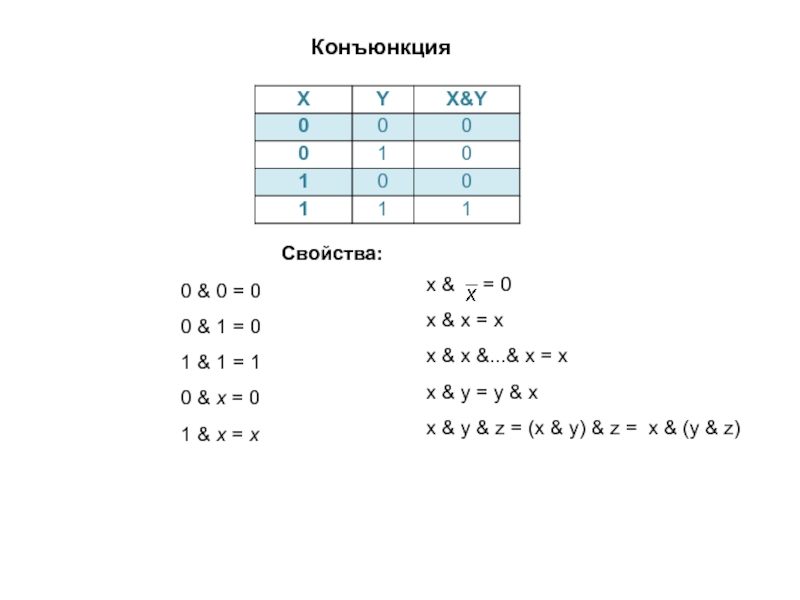
Слайд 9Конъюнкция
0 & 0 = 0
0 & 1 = 0
1 &
1 = 1
0 & x = 0
1 & x =
x
x & = 0
x & x = x
x & x &...& x = x
x & y = y & x
x & y & z = (x & y) & z = x & (y & z)
Свойства:
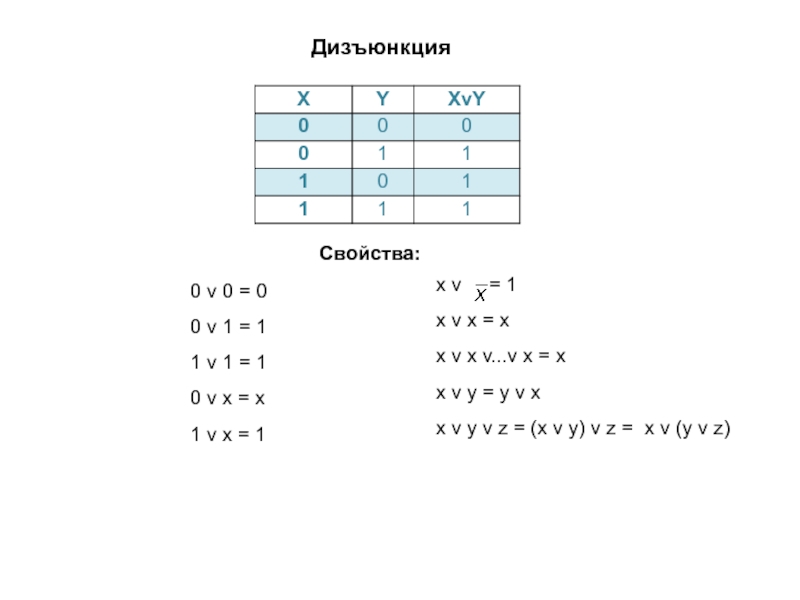
Слайд 10Дизъюнкция
0 v 0 = 0
0 v 1 = 1
1 v
1 = 1
0 v x = x
1 v x =
1
Свойства:
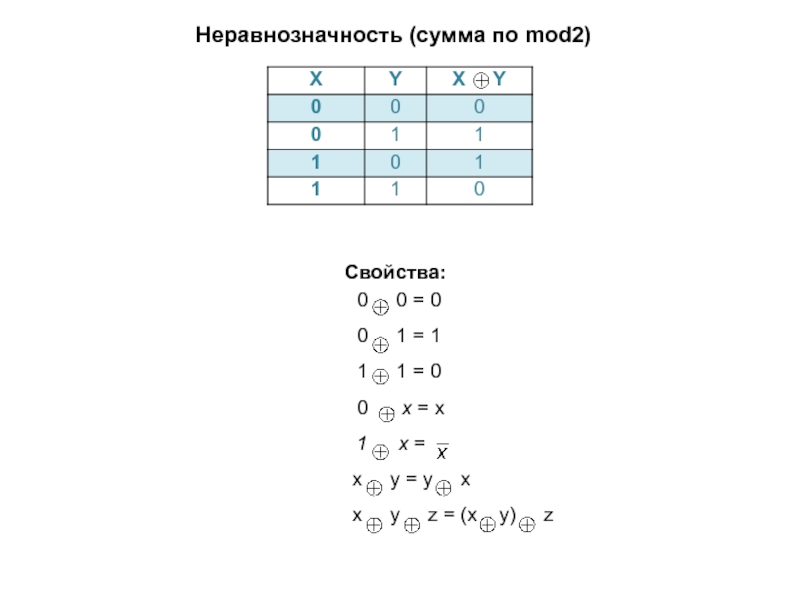
Слайд 13Неравнозначность (сумма по mod2)
Свойства:
Слайд 14Функция Fi, определяемая как
называется конъюнктивным термом.
Конъюнктивный терм, или
минтерм, или конституэнта единицы —связывает все переменные, представленные в прямой
или инверсной форме, знаком конъюнкции.
Представление логической функции
в виде совершенных нормальных форм
Слайд 16Теорема 1. Любая функция алгебры логики (ФАЛ) может быть представлена
аналитически в виде
f(x1 , x2, ... , xn) =
F1\/F2\/...\/Fk = \/Fi ,
где i — номера наборов, на которых функция равна 1; V — знак дизъюнкции, объединяющий все термы Fi , равные единице, k — количество наборов, для которых F = 1.
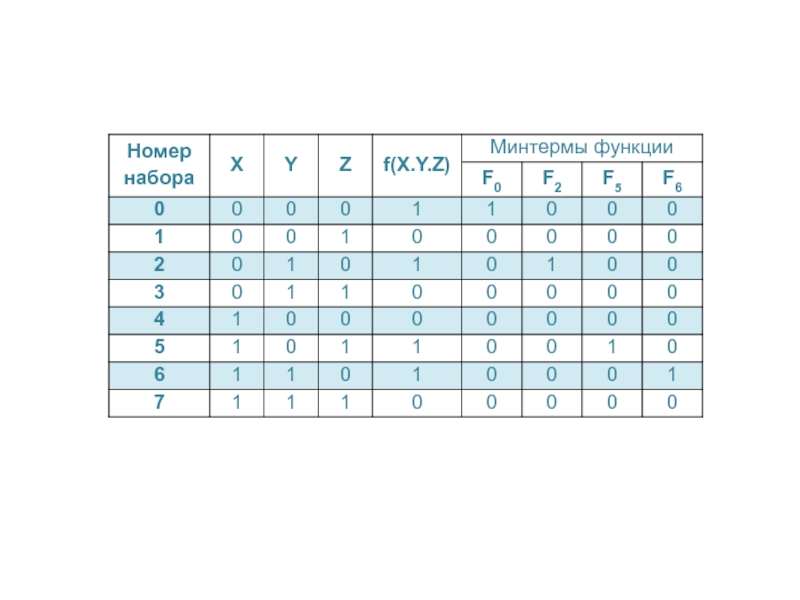
f(x.y.z) = V(0,2,5,6) = F0 \/ F2 \/ F5 \/F6 =
0 0 0 0 1 0 1 0 1 1 1 0
Слайд 17Теорема 1. Любая функция алгебры логики (ФАЛ) может быть представлена
аналитически в виде
f(x1 , x2, ... , xn) =
F1\/F2\/...\/Fk = \/Fi ,
где i — номера наборов, на которых функция равна 1; V — знак дизъюнкции, объединяющий все термы Fi , равные единице, k — количество наборов, для которых F = 1.
Совершенной дизъюнктивной нормальной формой (СДНФ) некоторой логической функции называется дизъюнкция всех конституэнт единицы этой ФАЛ. Любую ФАЛ, кроме константы «ноль», можно представить в виде СДНФ. Любая ФАЛ имеет единственную СДНФ с точностью до перестановки её членов.
Основные свойства СДНФ:
в СДНФ нет двух одинаковых минтермов;
в СДНФ ни один минтерм не содержит двух одинаковых переменных;
в СДНФ ни один минтерм не содержит вместе с переменной и её отрицание.
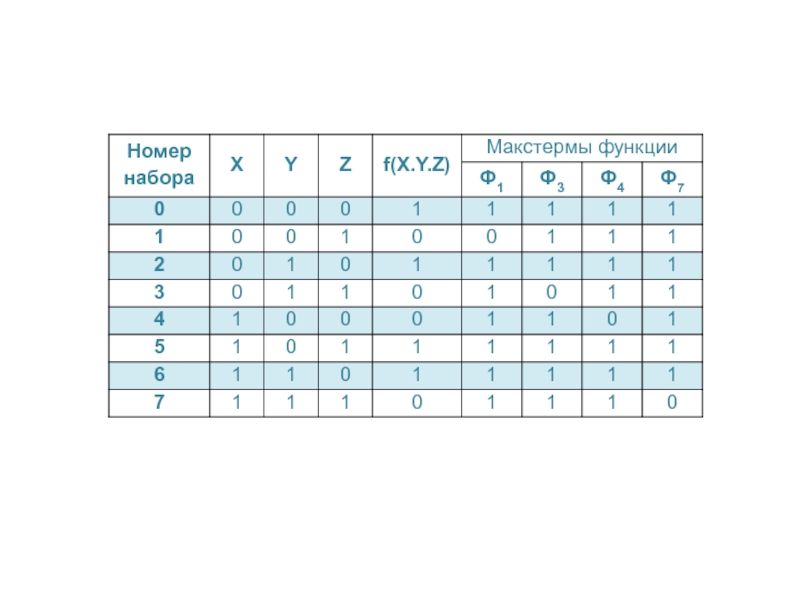
Слайд 18Функция Фi, определяемая как
называется дизъюнктивным термом.
Дизъюнктивный терм, или макстерм,
или конституэнта нуля связывает все переменные, представленные в прямой или
инверсной форме, знаком дизъюнкции.
Слайд 20Теорема 2. Любая ФАЛ может быть представлена аналитически в виде
f(x1 , x2, ... , xn) = Ф1 & Ф2
& ... & Фk = & Фi ,
где i — номера наборов, на которых функция равна 1; & — знак конъюнкции, объединяющий все термы Фi , равные нулю, k — количество наборов, для которых Ф = 0.
Совершенной конъюнктивной нормальной формой (СКНФ) некоторой логической функции называется конъюнкция всех конституэнт нуля этой ФАЛ. Любую ФАЛ, кроме константы «единица», можно представить в виде СКНФ. Любая ФАЛ имеет единственную СКНФ с точностью до перестановки её членов.
Основные свойства СКНФ:
в СКНФ нет двух одинаковых макстермов;
в СКНФ ни один макстерм не содержит двух одинаковых переменных;
в СКНФ ни один макстерм не содержит вместе с переменной и её отрицание.
Слайд 21Ранг терма r определяется количеством переменных, входящих в данный терм.
Минтермы и макстермы ФАЛ от n переменных имеют максимально возможный
ранг, равный n.
Слайд 22Элементарные конъюнкция и дизъюнкция — это те конъюнкции и дизъюнкции,
в которых каждая логическая переменная встречается не более 1 раза
(в виде основной логической переменной либо ее отрицания).
Дизъюнктивная нормальная форма (ДНФ) - это дизъюнктивное объединение элементарных конъюнкций различных рангов, включая ранг равный единице.
Конъюнктивная нормальная форма (КНФ) - это конъюнктивное объединение элементарных конъюнкций различных рангов, включая ранг равный единице.
Слайд 23Повышение ранга ДНФ и КНФ
a = a&b v a&^b
f(x,y,z) =
x&y&z v ^x&^z = x&y&z v ^x&y&^z v ^x&^y&^z
a =
(a v b)&(a v ^b)
f(x,y,z) = (x v y v ^z) & (x v ^y) = (x v y v ^z) & ( x v ^y v z) & (x v ^y v ^z)
Слайд 24Правило деМоргана
ЭКВИВАЛЕНТНОСТЬ ЛОГИЧЕСКИХ ФУНКЦИЙ
Логические функции называются эквивалентными (равнозначными), если они
принимают одинаковые значения на всех наборах переменных.
xy V xy =
x – операция склеивания
xy V xy = x V xy V xy – операция неполного склеивания
x V xy = x – операция поглощения
Слайд 25Полнота системы логических функций
Булева функция может быть представлена суперпозицией некоторого
набора функций { f1, f2, ... fn }/
Система элементарных логических
функций f1 . . . fm называется полной, если любую ФАЛ можно изобразить в виде суперпозиции (совокупности) функций f1 . . . fn.
Слайд 26Теорема. Пусть даны две системы логических функций:
F = {f1, f2,
... , fn} (1)
и
G = {g1, g2, ..., gm} (2).
Если система (1) полна и каждая её функция может быть выражена как суперпоозиция функций системы (2), тогда система (2) является полной.
Пример. Известно, система функций {И, ИЛИ, НЕ} является функционально полной (СДНФ, СКНФ).
Отсюда следует. что система ФАЛ, состоящая из одной функции «Штрих Шеффера», также функционально полна, так как:
Слайд 27 Правила перехода от представления ФАЛ в виде ДНФ
к функции,
представленной в базисе «Штрих Шеффера»:
если в ДНФ есть элементарные
конъюнкции, имеющие ранг 1, то повысить их ранг путём выполнения эквивалентного преобразования:
a = a &a или a = a &1;
в полученной ДНФ заменить все операции дизъюнкции и конъюнкции операциями «Штрих Шеффера»;
группы букв, соответствующие дизъюнктивным членам (эле
ментарным конъюнкциям), заключить в скобки.
Слайд 28 Правила перехода от представления ФАЛ в виде КНФ
к функции,
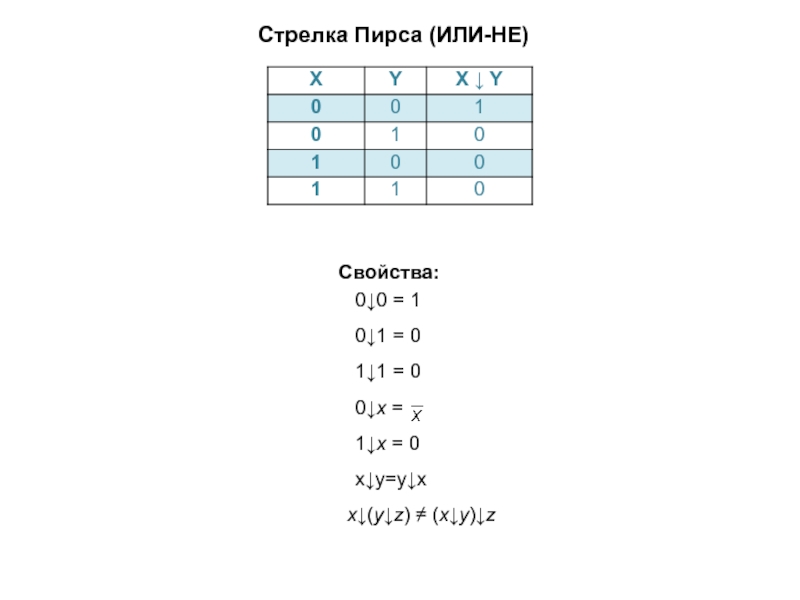
представленной в базисе «Стрелка Пирса»:
если в КНФ есть элементарные
конъюнкции, имеющие ранг 1, то повысить их ранг путём выполнения эквивалентного преобразования:
a = a v a или a = a v 0;
в полученной КНФ заменить все операции дизъюнкции и конъюнкции операциями «Стрелка Пирса»;
группы букв, соответствующие конъюнктивным членам (эле
ментарным дизъюнкциям), заключить в скобки.
Слайд 29Свойства логических функций
Переключательной функцией, сохраняющей нуль - называется функция, которая
на нулевом наборе аргументов т.е. на наборе
(0, 0, ...,
0, 0) равна нулю. Для переключательных функций, сохраняющих нуль, выполняется условие: f ( 0, 0, ..., 0, 0 ) = 0.
Переключательной функцией, сохраняющей единицу - называется функция, которая на единичном наборе аргументов т.е. на наборе
(1, 1, ..., 1, 1) равна единице. Для переключательных функций, сохраняющих единицу, выполняется условие: f ( 1, 1, ..., 1, 1 ) = 1.
Слайд 30При определении самодвойственности переключательной функции используется понятие противоположных наборов. Два
набора аргументов называются противоположными, если все значения аргументов одного набора
противоположны значениям аргументов другого набора. Чтобы получить противоположный набор, достаточно заменить в данном наборе нули единицами, а единицы нулями. Для функции трех аргументов следующие пары наборов являются противоположными:
000 и 111; 001 и 110; 010 и 101; 011 и 100.
В общем виде два противоположных набора записываются в виде (x1, x2, ..., xn) и
Переключательная функция n переменных f* (x1, x2, ..., xn) называется двойственной к функции f (x1, x2, ..., xn) , если имеет место равенство :
f* (x1, x2, ..., xn) =
Например, для функции дизъюнкции f (x1, x2) = x1 v x2 двойственной будет функция конъюнкции f* (x1, x2) = x1· x2.
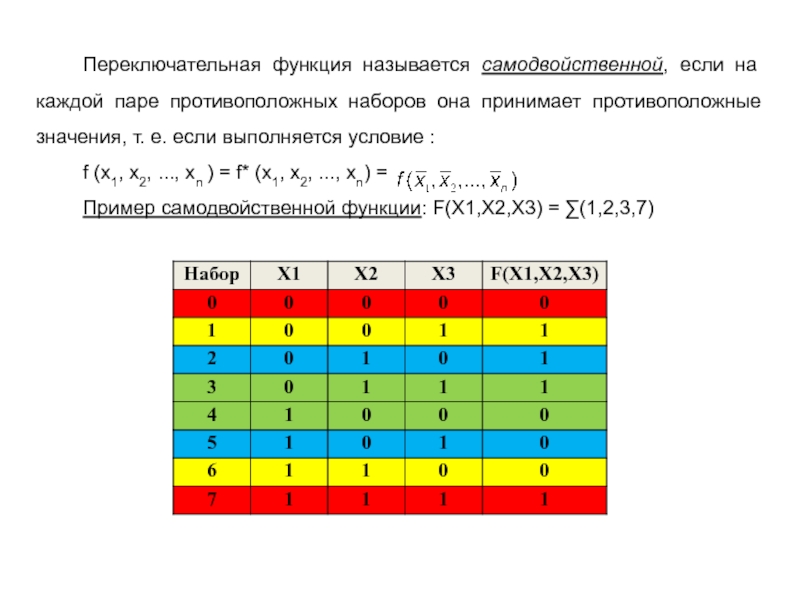
Слайд 31Переключательная функция называется самодвойственной, если на каждой паре противоположных наборов
она принимает противоположные значения, т. е. если выполняется условие :
f (x1, x2, ..., xn ) = f* (x1, x2, ..., xn) =
Пример самодвойственной функции: F(X1,X2,X3) = ∑(1,2,3,7)
Слайд 32При определении монотонности переключательной функции используется понятие сравнимости двух наборов
аргументов.
Примем условие, что 0 < 1. Два набора аргументов
X = (x1, x2, ..., xn) и Z = ( z1, z2, ..., zn ) называются сравнимыми, если для всех аргументов выполняется условие xi ≤ zi (говорят, что X ≤ Z). Иными словами, если значение каждого аргумента одного набора меньше или равно значению того же аргумента второго набора, то говорят, что первый набор меньше или равен второму ( не больше второго ).
Например, если X = (0000) и Z = (0001), то наборы сравнимы и X < Z.
Если же некоторые из значений аргументов первого набора больше или равны, а другие меньше значений тех же аргументов второго набора, то такие наборы называются несравнимыми.
Например, если X = (1010) и Z = (0110), то наборы являются несравнимыми.
Слайд 35Теорема Поста – Яблонского
о функциональной полноте
системы логических функций
Для того
чтобы система переключательных функций была функционально полной, необходимо и достаточно,
чтобы эта система включала:
- хотя бы одну переключательную функцию, не сохраняющую нуль;
- хотя бы одну переключательную функцию, не сохраняющую единицу;
- хотя бы одну нелинейную переключательную функцию;
- хотя бы одну немонотонную переключательную функцию;
- хотя бы одну несамодвойственную переключательную функцию.
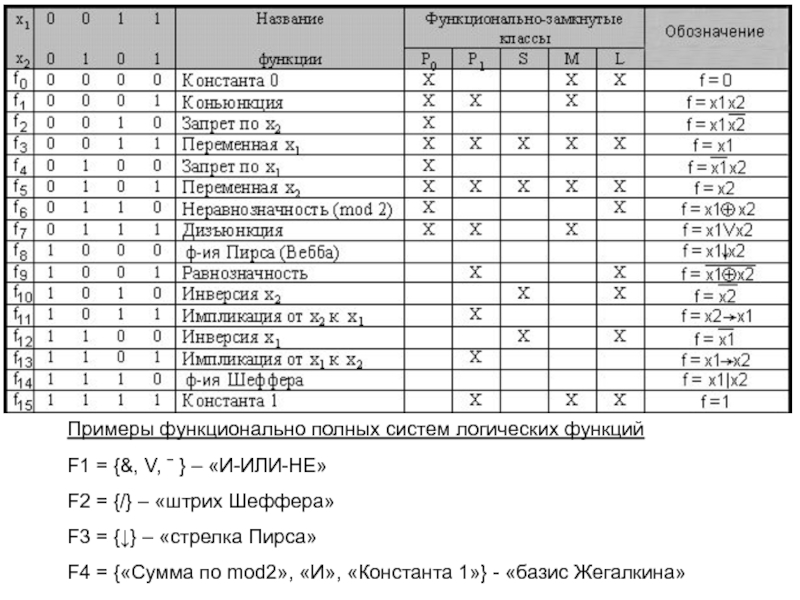
Слайд 36Примеры функционально полных систем логических функций
F1 = {&, V, ˉ
} – «И-ИЛИ-НЕ»
F2 = {/} – «штрих Шеффера»
F3 = {↓}
– «стрелка Пирса»
F4 = {«Сумма по mod2», «И», «Константа 1»} - «базис Жегалкина»
Слайд 37Теорема Яблонского
Из всякой полной системы логических функций можно выделить полную
подсистему, содержащую не более 4-х ФАЛ.
Определение.
Система функций F={f1, f2,…,fn} называется
базисом, если она полна, но всякая собственная подсистема не является полной.