Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логика
Содержание
- 1. Логика
- 2. Слайд 2
- 3. Слайд 3
- 4. Понятие – это форма мышления, а слово форма языка. Не следует отождествлять понятие и слово.
- 5. Другими словами, назначение слова - это служить наименованием предмета.
- 6. Например, понятие человек для всех народов имеет
- 7. Слайд 7
- 8. Слайд 8
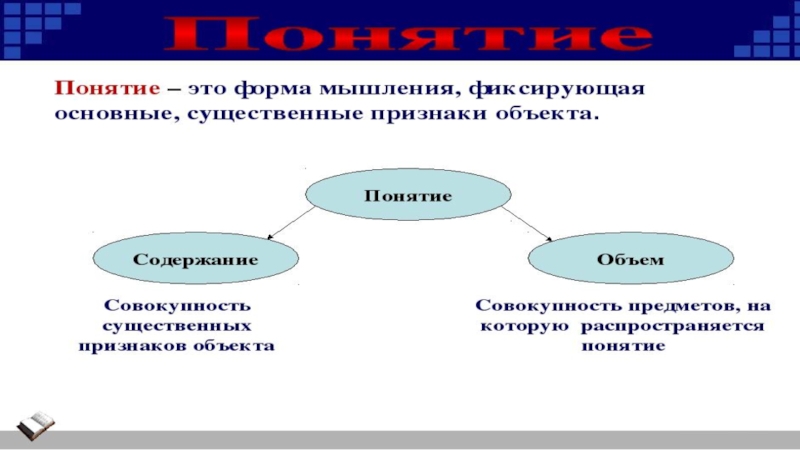
- 9. Содержание понятия – определяется на основе существенного
- 10. Объем понятия – это количество объектов, охватываемых
- 11. Все понятия по объему делятся на несколько
- 12. Наиболее общие понятия считаются категориями мышления. Это,
- 13. Слайд 13
- 14. Понятия бывают собирательными (рота солдат, коллектив, созвездие)
- 15. Анализ понятий производят по схеме: сначала
- 16. Понятие является определенным, когда оно имеет ясное
- 17. Причин появления неопределенных понятий несколько:1)многогранность и сложность
- 18. Метафора — незаменимое орудие разума, начальная форма
- 19. Неопределенность в художественном познании. Вот как описывает
- 20. В логике отношение между понятиями принято изображать
- 21. Понятия находятся в отношении пересечения, когда их
- 22. Понятия находятся в отношении подчинения, когда объем
- 23. Понятия находятся в отношении соподчинения, когда их
- 24. Понятия находятся в отношении противоположности, если они
- 25. Понятия находятся в отношении противоречия, если одно
- 26. До сих пор круговыми схемами Эйлера мы
- 27. Рассмотрим отношения между понятиями дедушка (Д), отец (О), мужчина (М), человек (Ч) с помощью схемы Эйлера.ДЧМО
- 28. Ограничения понятия, или переход от
- 29. Если к содержанию понятия геометрические фигуры (Г.ф.)
- 30. Обобщение понятия — это логическая операция
- 31. Сложение понятий—это логическая операция объединения двух и
- 32. Умножение понятий — это логическая операция объединения
- 33. Слайд 33
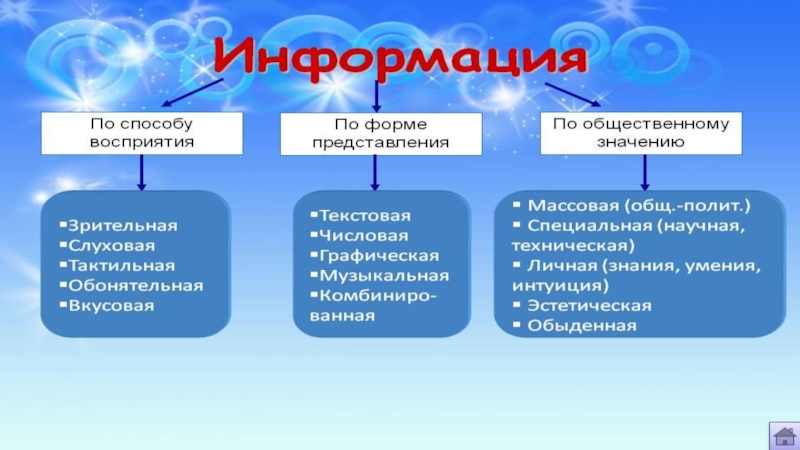
- 34. Рассмотрим сложность определения Информации
- 35. Слайд 35
- 36. Слайд 36
- 37. Слайд 37
- 38. Слайд 38
- 39. Скачать презентанцию
Слайды и текст этой презентации
Слайд 6 Например, понятие человек для всех народов имеет один смысл –
обозначение человека. Но понятие человек на разных языках выражается разными
словами.Французский – Homme ; Русский – челове́к
Испанский – Hombre; Итальянский – Uomo; Турецкий – adam; Немецкий - Mann ; Английский – man; Финский – Henki;
Слайд 9 Содержание понятия – определяется на основе существенного признака рассматриваемого объекта.
Так , содержание понятия человек связано с таким признаком, как
наличие разума. Содержание понятия мужчина определяют признаки: наличие разума и указание на половую принадлежность. Понятие русский мужчина, должен еще включать указание на национальность.Слайд 10 Объем понятия – это количество объектов, охватываемых этим понятием. Так,
объем понятия человек гораздо больше, чем понятия мужчина или женщина.
Объем понятия город гораздо большой, чем объем понятия столица. Между объемом и содержанием понятия существует обратное отношение : чем больше содержание понятия, тем меньше его объем, и наоборот.Слайд 11 Все понятия по объему делятся на несколько видов. Они бывают
единичными ,
т. е., входит один объект (например: Солнце, Москва,
Лев Толстой); общими , т.е. входят много предметов (например: небесное тело, город, писатель) и нулевыми , т.е. в объем не входят конкретные объекты(например: Баба –яга, Дед Мороз, вечный двигатель). Слайд 12 Наиболее общие понятия считаются категориями мышления. Это, например, обоснованные в
философии понятия: материя, движение, пространство, время, необходимость, случайность, причина, следствие,
явление, сущность. При познавательном процессе первоначальную ориентацию задают общие категории мышления, они, словно, определяют поле познавательной деятельности. Категории человеческого мышления в основном носят атрибутивный характер, хотя в историческом масштабе времени они корректируются, наполняются новым содержанием. Большой вклад в понимание смысла и значения категорий в человеческом мышлении внесли Аристотель, Кант и Гегель.Слайд 14
Понятия бывают собирательными
(рота солдат, коллектив, созвездие)
и не собирательными
(человек, растение, звезда).
По содержанию понятия бывают конкретными
(стол, гора, планета)
и абстрактными, обозначают не объект, а признак (мужество, глупость, темнота).По содержанию понятия бывают положительными, обозначают наличие чего-нибудь (школа, правда, тактичность) и отрицательными, обозначают
отсутствие чего-нибудь (неправда, бестактность).
Слайд 15 Анализ понятий производят по схеме: сначала выявляют объем и
содержание, потом определяют каким оно является: единичным, общим или нулевым,
затем устанавливают: оно собирательное или не собирательное, конкретное или абстрактное, наконец, положительное или отрицательное. Например: Солнце единичное, не собирательное, конкретное, положительное понятие; Созвездие Ориона – единичное, собирательное, конкретное и положительное понятие.Слайд 16 Понятие является определенным, когда оно имеет ясное содержание и четкий
объем. Например, мастер спорта является определенным понятием.
Понятие является неопределенным, когда
оно имеет неясное содержание и нечеткий объем. Например, хороший спортсмен, юный, старый являются неопределенными понятиями.Если в количественном отношении между объемом и содержанием понятия существует обратная связь, то в качественном отношении эта связь прямая: ясное содержание понятия обуславливает его четкий объем, неясное содержание - нечеткий объем.
Слайд 17
Причин появления неопределенных понятий несколько:
1)многогранность и сложность мира;
2)изменение, развитие, действительности;
3)субъективное
восприятие реальности.
Понятие неопределенности. Апейрон Анаксимандра. Принцип неопределенности Гейзенберга. Понятие неопределенности
в «Теории игр», «Синергетике»…Слайд 18 Метафора — незаменимое орудие разума, начальная форма отображения действительности. Искусство
и литература изобретают метафоры, наука их использует до появления логически
последовательных объяснений..Слайд 19 Неопределенность в художественном познании.
Вот как описывает Чичикова Гоголь:«В бричке
сидел господин не красавец, но и не дурной наружности, не
слишком толст, не слишком тонок, нельзя сказать, что стар, однако ж и не так чтобы слишком молод.»Слайд 20 В логике отношение между понятиями принято изображать с помощью круговых
схем Эйлера. Объемы понятий на них изображаются отдельными кругами.
К=Р.П.
Слайд 21 Понятия находятся в отношении пересечения, когда их объемы совпадают только
частично. Например, пересекающимися будут понятия школьник (Ш) и спортсмен (С):
есть школьники являющиеся спортсменами, и спортсмены являющиеся школьниками.С
Ш
Слайд 22 Понятия находятся в отношении подчинения, когда объем одного из них
обязательно больше объема другого и подчиняется ему. Например, в отношении
подчинения находятся понятия карась (К) и рыба (Р), так как все караси — это обязательно рыбы, но рыбами являются не только караси, но и другие виды рыб.РР
К
РР
Слайд 23 Понятия находятся в отношении соподчинения, когда их объемы не имеют
общих элементов, но в то же время входят в объем
какого-то третьего понятия, подчиняясь ему совместно. Например, понятия сосна (С) и береза (Б) являются соподчиненными: ни одна сосна не может быть березой, и наоборот. Но оба понятия являются деревья.Б
С
Д
Слайд 24 Понятия находятся в отношении противоположности, если они обозначают какие-то взаимозаключающие
признаки, крайние состояния чего-либо, между которыми, однако, всегда есть некий
средний, переходный вариант.Например, понятия высокий человек (В.ч.) и низкий человек (Н.ч.)
В.ч.
Н.ч.
Слайд 25 Понятия находятся в отношении противоречия, если одно из них представляет
собой отрицание другого, причем в отличие от противоположных понятий между
противоречащими понятиями не может быть среднего варианта. Например, в отношении противоречия находятся понятия высокий человек (В.ч) и низкий человек (Н.ч.).В.ч.
Н.ч.
Слайд 26 До сих пор круговыми схемами Эйлера мы изображали в основном
отношения между двумя понятиями, но это можно сделать для большого
числа понятий. Например, отношения между понятиями боксёр (Б), негр (Н) и человек (Ч) изображаются следующей схемой Эйлера.Б
Н
Ч
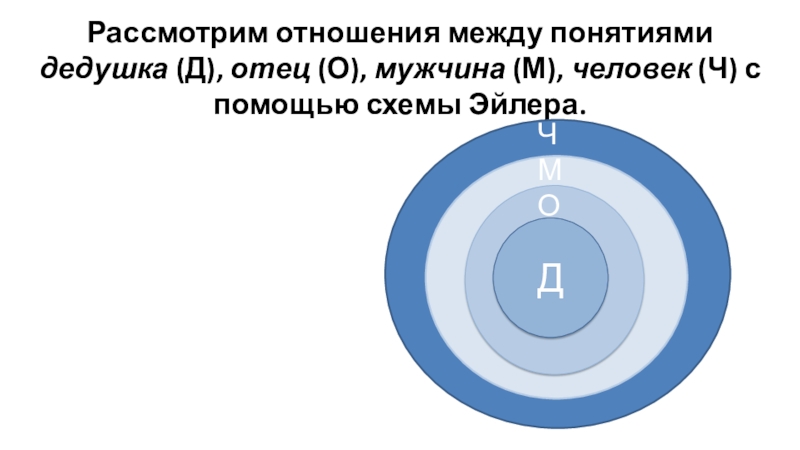
Слайд 27Рассмотрим отношения между понятиями дедушка (Д), отец (О), мужчина (М),
человек (Ч) с помощью схемы Эйлера.
Д
Ч
М
О
Слайд 28 Ограничения понятия, или переход от родового понятия к видовому, —
это уменьшение его объема, а значит — увеличение содержания. Вот
почему при добавлении каких–либо признаков к содержанию понятия автоматически уменьшается его объем. Например, если к содержанию понятия физический прибор (Ф.п.) прибавить признак измерять напряжение электрического тока, то оно превратиться в понятие вольтметр (В), которое будет видовым по отношению к исходному родовому понятию физический прибор.В
Родовое
Ф.п.
Видовое
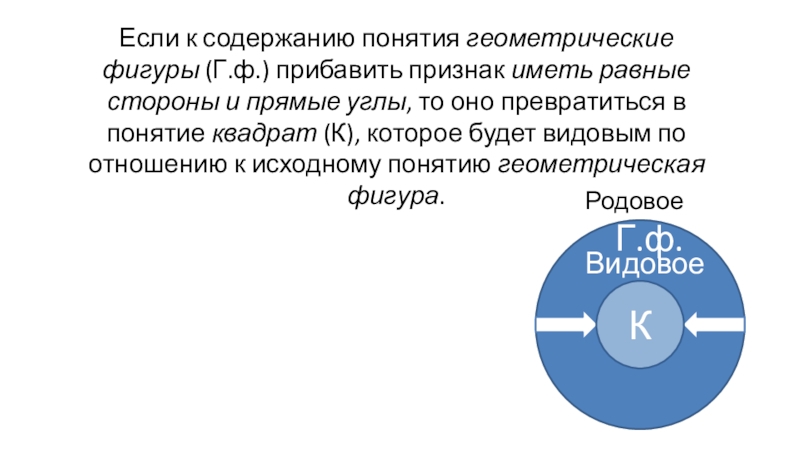
Слайд 29Если к содержанию понятия геометрические фигуры (Г.ф.) прибавить признак иметь
равные стороны и прямые углы, то оно превратиться в понятие
квадрат (К), которое будет видовым по отношению к исходному понятию геометрическая фигура.К
Родовое
Г.ф.
Видовое
Слайд 30 Обобщение понятия — это логическая операция перехода от видового
понятия к родовому с помощью исключения из его содержания какого-либо
признака (или нескольких признаков).Например, если от содержания понятия биология (Б) отбросить признак изучать различные формы жизни, то оно превратиться в понятие наука (Н), которое будет родовым по отношению к исходному видовому понятию биология (Б).
Б
Родовое
Н
Видовое
Слайд 31 Сложение понятий—это логическая операция объединения двух и более понятий, в
результате которой образуется новое понятие с объемом, охватывающим собой все
элементы объемов исходных понятий. Например, при сложении понятий школьник (Ш) и спортсмен (С) образуется новое понятие, в объем входят как все школьники, так и все спортсмены.С
Ш
Слайд 32 Умножение понятий — это логическая операция объединения двух и более
понятий, в результате которой образуется новое понятие с объемом, охватывающим
собой только сопадающие элементы объемов исходных понятий. Например, при умножении понятий школьник (Ш) и спортсмен (С) образуется новое понятие, в объем которого входят только школьники являющиеся спортсменами, и спортсмены, являющиеся школьниками.С
Ш