МАЛОИЗВЕСТНЫЕ, но очень интересные ТЕОРЕМЫ ПЛАНИМЕТРИИ Подготовила: Парнева

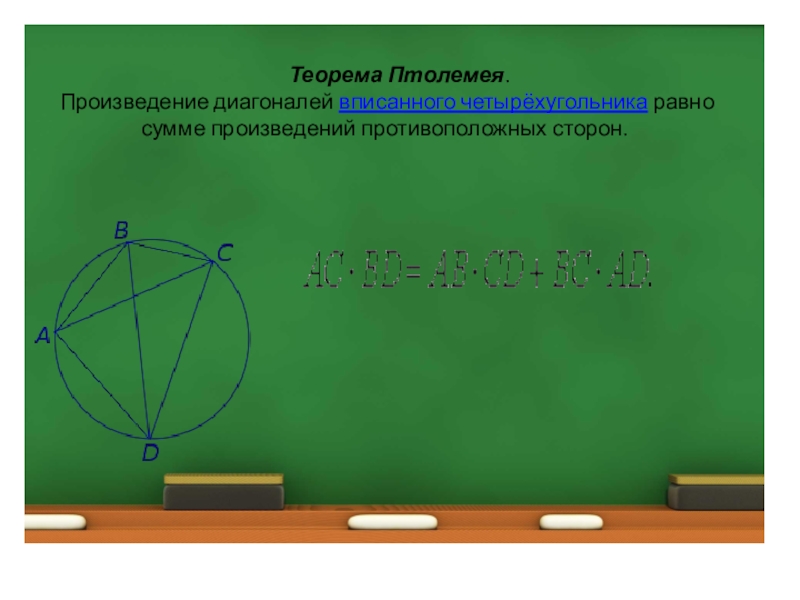
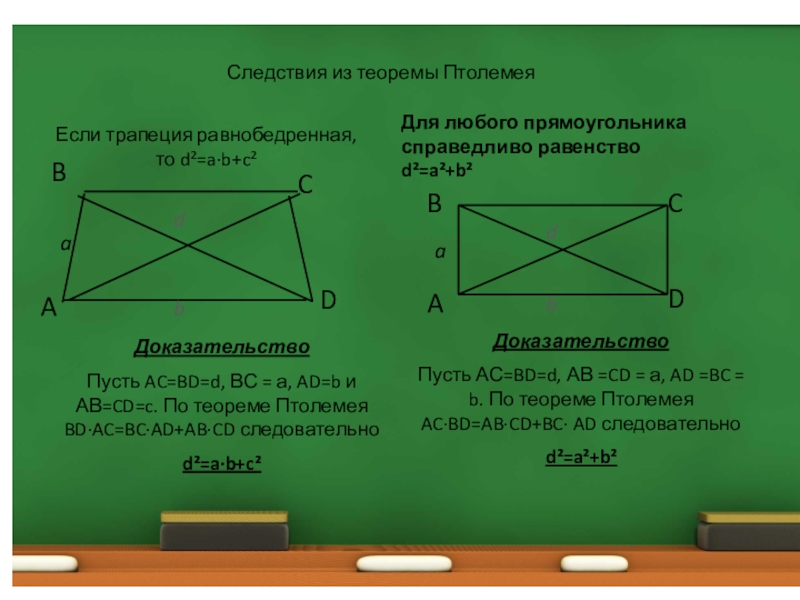
Анастасия Алексеевна,
обучающаяся МКОУ «Устьевская СОШ»
Руководитель:
Кустова Людмила Анатольевна,
учитель информатики

и математики
МКОУ «Устьевская СОШ»



-------

вызваны следующими фактами: Часто в олимпиадных заданиях по математике, в

КИМ ЕГЭ и ОГЭ встречаются задачи по геометрии, решение, которых вызывают затруднения, и чтобы их решить требуется много времени.
объект исследования
малоизвестные теоремы и свойства планиметрии.
гипотеза исследования
- Существуют малоизвестные теоремы и свойства геометрии, знание которых облегчит решение некоторых планиметрических задач
цель работы : выявить, доказать малоизвестные теоремы, свойства геометрии.
задачи работы и методы исследования
1. Изучить учебную и справочную литературу.
2.Собрать малоизвестный теоретический материал, необходимый для решения планиметрических задач.
3.Разобраться в доказательствах малоизвестных теорем и свойств.
4. Найти и решить задачи, на применение этих малоизвестных теорем и свойств.

угла, равна половине гипотенузы.

Теорема (обратная). Если медиана треугольника равна половине

стороны, к которой она проведена, то треугольник прямоугольный

сторон.      

= а, AD=b и АВ=CD=c. По теореме Птолемея BD·AC=BC·AD+AB·CD следовательно

d²=a·b+c²

Для любого прямоугольника справедливо равенство d²=a²+b²

Доказательство
Пусть АС=BD=d, АВ =CD = а, AD =BC = b. По теореме Птолемея AC·BD=AB·CD+BC· AD следовательно
d²=a²+b²

Найти диагональ BD.
Дано: ABCD – выпуклый четырехугольник,
AB = 25,BC =

60,CD = 52,AD = 39,диагональ AC = 65 .
Найти: BD.

Решение:
Так как 25 ² + 60 ² = 65 ² и 39 ² + 52 ² = 65 ², то по теореме обратной теореме Пифагора, треугольники ABC и ADC прямоугольные. Следовательно, ∟B + ∟D = 90 º + 90 º = 180 º. Значит, около четырёхугольника ABCD можно описать окружность. Для вписанного в окружность четырёхугольника применим теорему Птолемея:
AC · BD = AB · CD + AD · BC,
65·BD = 39 · 60 + 25 · 52 , откуда BD = 56.

же окружности. Пусть хорды AD и ВС пересекают хорду PQ в точках X и Y. Тогда М является серединой отрезка XY.
теорема Бабочки.

то есть существуют малоизвестные теоремы и утверждения геометрии, знание которых

облегчит решение некоторых планиметрических задач.

Задачи на будущее:
Следующим шагом моей работы будет, как раз продолжение работы над исследование теорем о бабочке и теорем Менелая и Чевы.