Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математические основы криптологии
Содержание
- 1. Математические основы криптологии
- 2. Форма отчетностиФорма отчетности – зачет.Для получения оценки
- 3. Литература:Коробейников А.Г., Гатчин Ю.А. Математические основы криптологии.
- 4. ЗНАТЬ:основные операции математической логики;основные методы, используемые криптологией;свойства
- 5. СодержаниеЭлементы теории чисел.Модулярная арифметикаНОД, НОК чисел. Алгоритм
- 6. 1. Элементы теории чисел1.1 Модулярная арифметика
- 7. Слайд 7
- 8. 1.2 Вычисление степени числа по модулю
- 9. 1.3 НОД и НОК чисел
- 10. Алгоритм ЭвклидаПример. Применим алгоритм Евклида к нахождению
- 11. 2 Основные определения и термины криптологииКриптология –
- 12. Основные термины криптологииОдним из основных понятий криптографии
- 13. Что такое криптография?Наука о томкак сделать информацию
- 14. Основные задачи криптографииВ узком контексте сетевой безопасности
- 15. Алиса и БобВ криптографических протоколах часто приходится
- 16. Классификация систем шифрования
- 17. 3 Исторические этапы развития криптографии
- 18. 3.1 Основные исторические вехиДревний миржрецы и правители
- 19. Виды шифрующих преобразованийШифры перестановки преобразуют открытый текст
- 20. 3.2 Шифры перестановки. 1. Шифр СкиталлаСпециальный
- 21. Потом ремень сматывался и получался вот такой
- 22. 2. Шифрующие таблицы ТрисемусаШифрующие таблицыВ качестве ключа
- 23. 3. Магические квадратыМагическим квадратом называется квадратная таблица
- 24. 1.1 Шифр ЦезаряКлюч: 3 Oткрытый текст: Р
- 25. Слайд 25
- 26. Попробуйте расшифровать!КГЬЛХГАБВГДЕЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯГДЕЖ3ИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯАБВ
- 27. Получилось слово:Защита
- 28. АТАКА «ГРУБОЙ СИЛЫ» НА ШИФР ЦЕЗАРЯАтакой методом
- 29. 1.2 Афинная подстановка ЦезаряОпределим преобразование:- целые числа
- 30. 1.3 Шифр Цезаря с ключевым словомСистема Цезаря
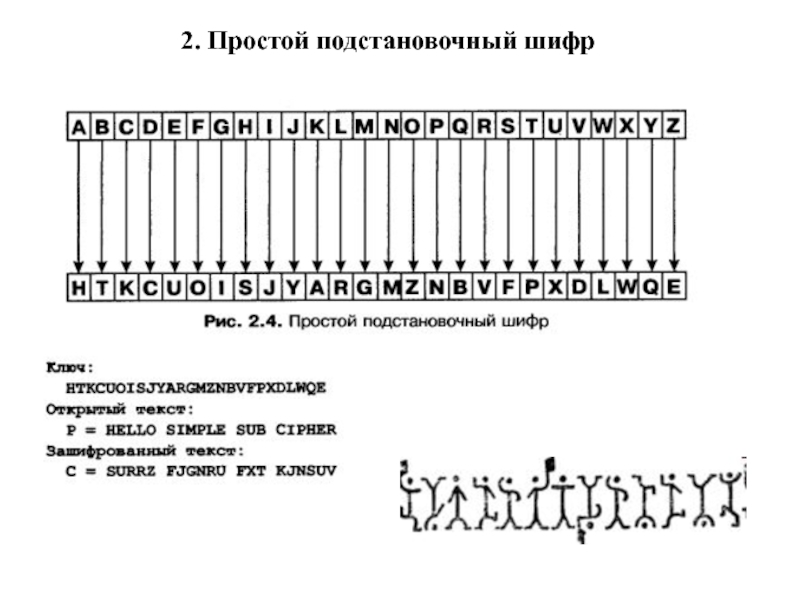
- 31. 2. Простой подстановочный шифр
- 32. 3. Шифр МирабоРазделим алфавит на 6 групп.В
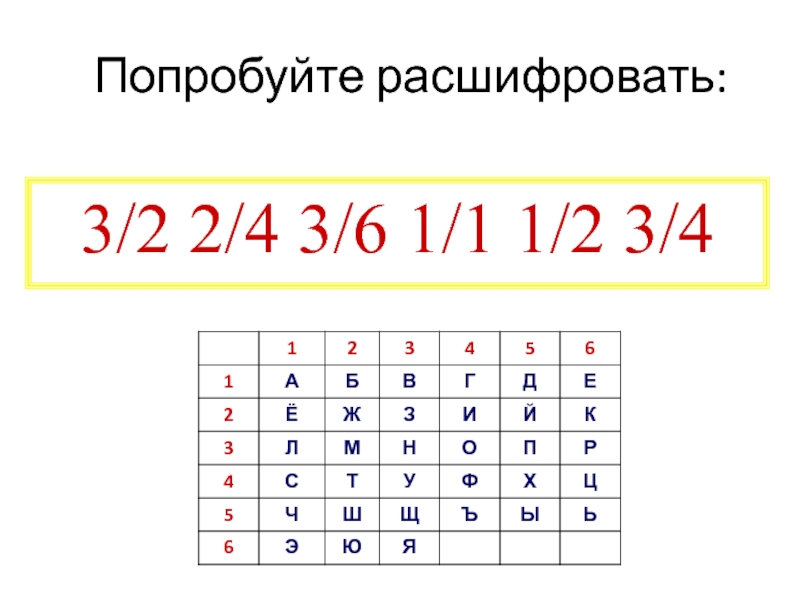
- 33. Попробуйте расшифровать:3/2 2/4 3/6 1/1 1/2 3/4
- 34. Получилось:Мирабо
- 35. 4. Полибианский квадратВ Древней Греции, за два
- 36. 5. Шифрующие таблицы Трисемуса
- 37. получаем шифртекстПДКЗЫВЗЧШЛЫЙСЙТакие табличные шифры называются монограммными, так
- 38. 6. Биграммный шифр ПлейфераШифр Плейфейра, изобретенный в
- 39. Зашифруем текстВСЕ ТАЙНОЕ СТАНЕТ ЯВНЫМРазбиение этого текста
- 40. ГП ДУ ОВ ДЛ НУ ПД ДР
- 41. ЧАСТОТНЫЙ АНАЛИЗ: РАСКРЫТИЕ ПОДСТАНОВОЧНОГО ШИФРАДля раскрытия простых
- 42. 3.4 Система омофоновСистема омофонов обеспечивает простейшую защиту
- 43. Вскрытие шифра простой замены в случае длинного
- 44. 3.5 Шифры сложной замены. 1. Шифр Виженера.С
- 45. Слайд 45
- 46. Шифр ВИЖЕНЕРА В шифре Виженера такая таблица
- 47. АТАКА БЭББИДЖА: РАСКРЫТИЕ ШИФРА ВИЖЕНЕРАБэббидж обнаружил, что
- 48. После тoгo как длина ключа будет, предположительно,
- 49. 2. Роторные машины. Энигма.Наиболее сложными являлись т.н.
- 50. Машина ЛоренцаМашина Лоренца (Lorenz-Chiffre, Schlüsselzusatz; Lorenz SZ
- 51. Вскрытие роторных машинВо время Второй мировой войны
- 52. 3.6 Шифры гаммированияШироко распространенные примеры шифра данного
- 53. Вскрытие шифров гаммирования. Периодическая и предсказуемая гаммаОдним
- 54. 3.7 Единственный неуязвимый шифр: ОДНОРАЗОВЫЙ ШИФРОВАЛЬНЫЙ
- 55. Единственный неуязвимый шифр: ОДНОРАЗОВЫЙ ШИФРОВАЛЬНЫЙ БЛОКНОТ
- 56. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Математические основы криптологии
Чтоб мысль врага узнать,
ему вскрывают сердце.
А письма —
и подавно...
Шекспир , "Король Лир"Слайд 2Форма отчетности
Форма отчетности – зачет.
Для получения оценки необходимо набрать за
семестр от 60 до
100 баллов:П – посещение; З – защита ЛР
Слайд 3Литература:
Коробейников А.Г., Гатчин Ю.А. Математические основы криптологии. – С.Пб: ИТМО,
2004. – 109 с.
Математические и компьютерные основы криптологии: Учебное пособие
/ Ю.С. Харин, В.И. Берник, Г.В. Матвеев, С.В. Агиевич. – Мн.: Новое знание, 2003. – 382 с.Тилборг ван Х.К.А. Основы криптологии. Профессиональное руководство. – М.: Мир, 2006. – 471 с.
Галуев Г.А. Математические основы криптологии. Таганрог: ТРТУ, 2003. – 120 с.
Поповский В.В., Персиков А.В. Основы криптографической защиты информации в телекоммуникационных системах. Том 1: Учебник. – ООО «Компания СМИТ», 2010. – 352 с.
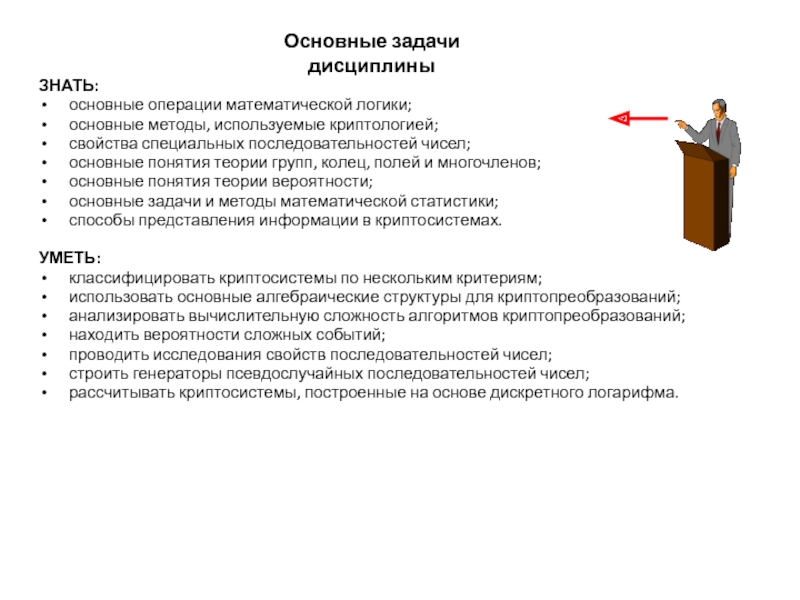
Слайд 4ЗНАТЬ:
основные операции математической логики;
основные методы, используемые криптологией;
свойства специальных последовательностей чисел;
основные
понятия теории групп, колец, полей и многочленов;
основные понятия теории вероятности;
основные
задачи и методы математической статистики;способы представления информации в криптосистемах.
УМЕТЬ:
классифицировать криптосистемы по нескольким критериям;
использовать основные алгебраические структуры для криптопреобразований;
анализировать вычислительную сложность алгоритмов криптопреобразований;
находить вероятности сложных событий;
проводить исследования свойств последовательностей чисел;
строить генераторы псевдослучайных последовательностей чисел;
рассчитывать криптосистемы, построенные на основе дискретного логарифма.
Основные задачи дисциплины
Слайд 5Содержание
Элементы теории чисел.
Модулярная арифметика
НОД, НОК чисел. Алгоритм Эвклида
2. Основные определения
и термины криптографии. Классификация систем шифрования.
3. Исторические этапы развития криптографии.
Этапы
развитияШифры перестановок
Шифры подстановок
Шифры гаммирования
4. Основные свойства многочленов над полем. Группы. Кольца. Поля. Многочлены.
Классификация современных шифров
Современные симметричные шифры: примеры, достоинства, недостатки
5. Модульная арифметика. Теория вычетов.
Функция Эйлера.
Нахождение обратных элементов: Цепные дроби. Расширенный алгоритм Эвклида.
Китайская теорема об остатках.
Квадратичные вычеты
Современные асимметричные шифры: примеры (RSA, El-Gamal, Polig-Hellman), достоинства, недостатки
Гибридные шифры
6. Основы математической логики. Стойкость криптосистем.
7. Криптосистемы на эллиптических кривых.
8. Однонаправленные функции в криптографии.
Хеш-функции: примеры, свойства, сферы применения
Понятие ЭЦП. Алгоритмы ЭЦП: DSA, El-Gamal
9. Алгоритмы распределения ключей.
Слайд 10Алгоритм Эвклида
Пример. Применим алгоритм Евклида к нахождению (175, 77).
175 =
77*2 + 21, 77 = 21*3 +
14, 21 =14*1 + 7, 14 = 7*2.Последний положительный остаток — r3 = 7. Значит, (175, 77) = 7.
Слайд 112 Основные определения и термины криптологии
Криптология – наука о создании
и анализе систем безопасности, предметом которой являются математические основания криптографии
и криптоанализа.Криптография – наука о принципах, средствах и математических методах преобразования информации, с целью сокрытия смысла или структуры данных, а также для защиты их от несанкционированного использования или подделки. Одним из основных методов криптографии является шифрование.
Криптоанализ – наука о методах раскрытия шифров или подделки данных. Поскольку проверка шифров на стойкость является обязательным элементом их разработки, криптоанализ также является частью процесса разработки.
Шифрованием называется взаимно однозначное преобразование сообщения, с целью скрытия его смысла от посторонних.
Исходный текст сообщения, который должен быть защищен называется открытый текст.
Результат шифрования – шифрованный текст (шифротекст, криптограмма).
Совокупность данных, определяющих конкретное преобразование из множества преобразований шифра называют ключом.
Открытый текст состоит из элементов, которые определяются шифрпреобразованием.
Элемент – это наименьшая часть данных, (набор битов), которая может быть зашифрована. Элементам открытого текста соответствуют элементы шифртекста.
Слайд 12Основные термины криптологии
Одним из основных понятий криптографии является стойкость.
Стойкость
– это способность противостоять попыткам хорошо вооруженного современной техникой и
знаниями криптоаналитика дешифровать перехваченный шифротекст, раскрыть ключи шифра или нарушить целостность и подлинность информации.Криптоаналитической атакой называют использование специальных методов для раскрытия ключа шифра и/или получения открытого текста. Предполагается, что атакующей стороне уже известен алгоритм шифрования, и ей требуется только найти конкретный ключ.
Другая важная концепция связана с термином «взлом». Когда говорят, что некоторый алгоритм был «взломан» , это не обязательно означает, что найден практический способ раскрытия шифрованных сообщений. Moжет иметься в виду в виду, что найден способ существенно уменьшить ту вычислительную работу, которая требуется для раскрытия шифрованного сообщения методом «грубой силы», то есть простым перебором всех возможных ключей.
При осуществлении такого взлома практически шифр все же может оставаться стойким, поскольку требуемые вычислительные возможности будут все еще оставаться за гранью реального. Oднако, хотя существование метода взлома не означает еще реальной уязвимости алгоритма, обычно такой алгоритм более не используют.
Слайд 13Что такое криптография?
Наука о том
как сделать информацию конфиденциальной, избирательно доступной
(шифрование)
как обеспечить целостность данных
как обеспечить аутентификацию (достоверную идентификацию)
субъекта: аутентичность информационного
источникаобъекта: пользователя, процесса
как обеспечить доказательность действия (неотказуемость)
как обеспечить контроль доступа (авторизацию)
Предмет науки:
криптографические алгоритмы (математика)
криптографические протоколы (процессы с использованием криптографических алгоритмов)
Принцип (Август Керхоффс, 1835-1903):
вся защита должна основываться только на качестве (длине, энтропии) ключа
алгоритмы должны быть тщательно выверены и публично доступны
Метод:
для того, чтобы выполнить криптографическую операцию (за исключением, м.б., обеспечения целостности данных), нужно знать секретную информацию (ключ)
незнающий ключа должен «искать иголку в стоге сена» (а «стог» должен быть достаточно большим в математическим смысле)
Слайд 14Основные задачи криптографии
В узком контексте сетевой безопасности основными задачами криптографии
являются
конфиденциальность данных:
цель: сделать данные «нечитаемыми» для непосвященных
метод: шифрование
целостность и имитостойкость
данныхцель: исключить возможность умышленного и неумышленного изменения (искажения) данных неуполномоченными лицами
метод: хэш, имитовставка, электронно-цифровая подпись
аутентификация субъекта – доказательство того, что субъект действия является именно тем, за кого себя выдает
аутентификация источника данных – доказательство того, что данные изданы определенным субъектом и являются подлинными (т.е. никем другим не искажены; в этом смысле – аутентификация источника данных автоматически обеспечивает их целостность)
обеспечение безотказности – невозможности для субъекта, выполнившего некоторое действие, впоследствии отказаться от факта выполнения этого действия
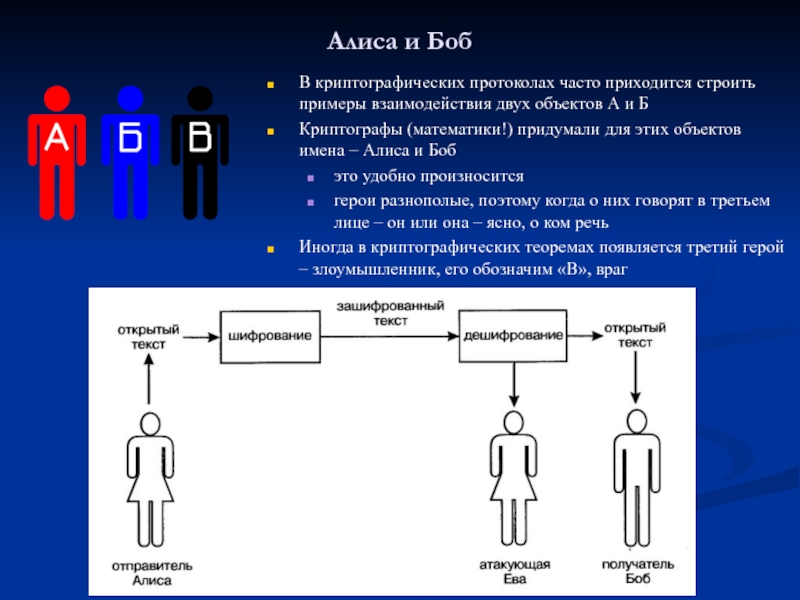
Слайд 15Алиса и Боб
В криптографических протоколах часто приходится строить примеры взаимодействия
двух объектов А и Б
Криптографы (математики!) придумали для этих объектов
имена – Алиса и Бобэто удобно произносится
герои разнополые, поэтому когда о них говорят в третьем лице – он или она – ясно, о ком речь
Иногда в криптографических теоремах появляется третий герой – злоумышленник, его обозначим «В», враг
Слайд 183.1 Основные исторические вехи
Древний мир
жрецы и правители Египта, Греции, Рима
перестановочный
шифр Цезаря
Средние века
c Х века: церковь («Полиграфия Трисемуса», 1508г.)
с XVI
века: политики (Мария Стюарт)Гражданская война в США («Цилиндр Джефферсона», возможно, первая шифровальная машина)
1я мировая война: Циммерман
2я мировая война: Энигма, Алан Тьюринг
1948: теория информации Клода Шеннона
1974: разработка первого криптостандарта (DES)
1976: изобретение системы шифрования с открытым ключом (Витфилд Дифи и Мартин Хеллман)
1978: система электронно-цифровой подписи (Роналд Райвест, Ади Шамир, Леонард Адлеман)
1980е: первые открытые интернациональные исследования, создание международного центра разработки криптографических систем (International Association for Cryptographic Research, IACR, 1987)
c 1990х: окончательная утрата занавеса секретности вокруг темы криптографии, либерализация законодательств распространения и применения криптосредств, повсеместное применение средств криптографии в программном обеспечении, коммуникациях, электронной коммерции
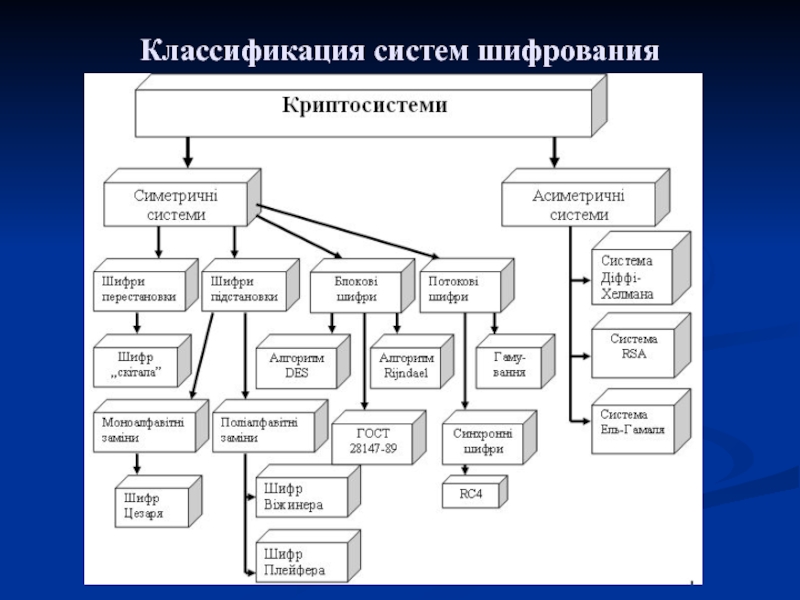
Слайд 19Виды шифрующих преобразований
Шифры перестановки преобразуют открытый текст таким образом, что
его символы переставляются по определенному правилу в пределах некоторого блока
этого текста.Шифры простой замены (подстановки) преобразуют открытый текст таким образом, что каждый его символ заменяется на какой-нибудь другой. При этом одинаковым символам открытого текста соответствуют одинаковые символы шифртекста, а разным – разные. Ключом является таблица, которая указывает в какой именно символ шифртекста переходит символ открытого текста. Без утраты общности можно стчитать, что сообщение и шифртекст записывают в одном и том же алфавите, так как использование экзотических символов не сделает шифр надежнее. Сделав это допущение, можно легко подсчитать количество всех возможных ключей для шифра подстановки. Для алфавита из 32 букв это 32! = 2,63130 ⋅ 1035 ключей. Следует отметить, что комбинация шифров замены – перестановки образуют все многообразие применяемых на практике симметричных шифров.
Шифры сложной замены (полиподстановки) преобразуют открытый текст таким образом, что каждый его символ заменяется на символ из различного алфавита. При этом одинаковым символам открытого текста могут соответствовать разные символы шифртекста.
Шифры гаммирования преобразуют открытый текст таким образом, что символы открытого текста, предварительно заменяемые на числа, складываются по модулю с элементами некоторой числовой последовательности, которая называется гаммой.
Слайд 203.2 Шифры перестановки.
1. Шифр Скиталла
Специальный жезл для шифрования –
СКИТАЛЛА, применялся для шифра перестановки. Он был изобретён в древней
"варварской" Спарте во времена Ликурга в V в.Для шифрования текста использовался цилиндр заранее обусловленного диаметра. На цилиндр наматывался тонкий ремень из пергамента, и текст выписывался построчно вдоль оси цилиндра.
Наступаем
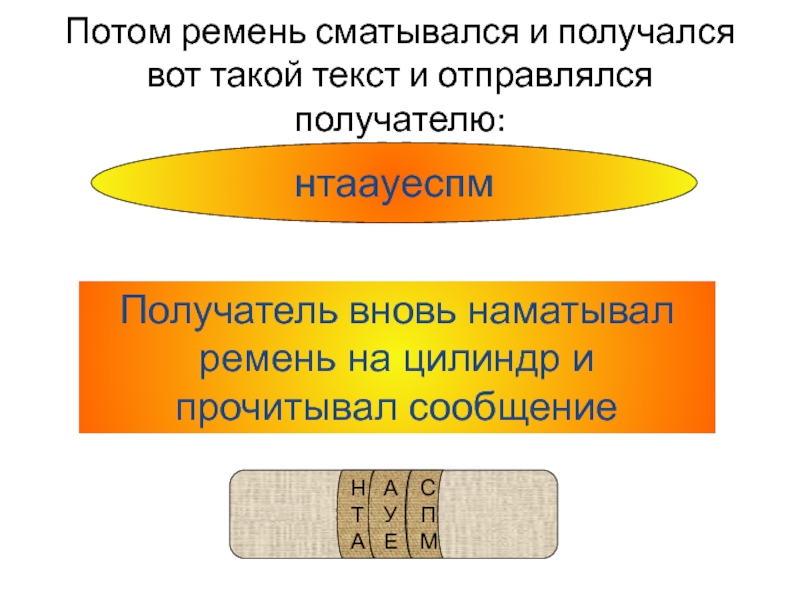
Слайд 21Потом ремень сматывался и получался вот такой текст и отправлялся
получателю:
нтаауеспм
Получатель вновь наматывал ремень на цилиндр и прочитывал сообщение
Слайд 222. Шифрующие таблицы Трисемуса
Шифрующие таблицы
В качестве ключа в шифрующих таблицах
используются:
- размер таблицы;
- слово или фраза, задающие перестановку;
- особенности
структуры таблицы.Один из самых примитивных табличных шифров – простая перестановка, для которой служит ключом размер таблицы. Сообщение записывается в таблицу поочередно по столбцам. Для формирования шифртекста сообщение считывают по строкам.
Например. Открытое сообщение: ПРИЛЕТАЮДВАДЦАТОГО.
Шифртекст: ПЛАВЦОРЕЮААГИТДДТО.
Для расшифровки, естественно, выполняют обратную процедуру. Вписывают шифртекст по строкам и считывают по столбцам для получения открытого текста. Отправитель и получатель сообщения заранее уславливаются об общем ключе - конфигурации таблицы.
Слайд 233. Магические квадраты
Магическим квадратом называется квадратная таблица с вписанными в
клетки натуральными числами, начиная с 1, которые дают в сумме
по каждому столбцу, каждой строке и каждой диагонали одно и то же число.Шифруемый текст вписывается в магические квадраты в соответствии с нумерацией клеток, а считываем содержимое таблицы по строкам и получаем шифротекст.
Например.
Открытый текст: ПРИЛЕТАЮ ВОСЬМОГО.
Магический квадрат:
Шифртекст: ОИРМЕОСЮВТАЬЛГОП.
Количество магических квадратов быстро возрастает с увеличением размера квадрата. Например, существует 880 квадратов с данными свойствами размером 4×4, а размером 5×5 уже около 250 000.
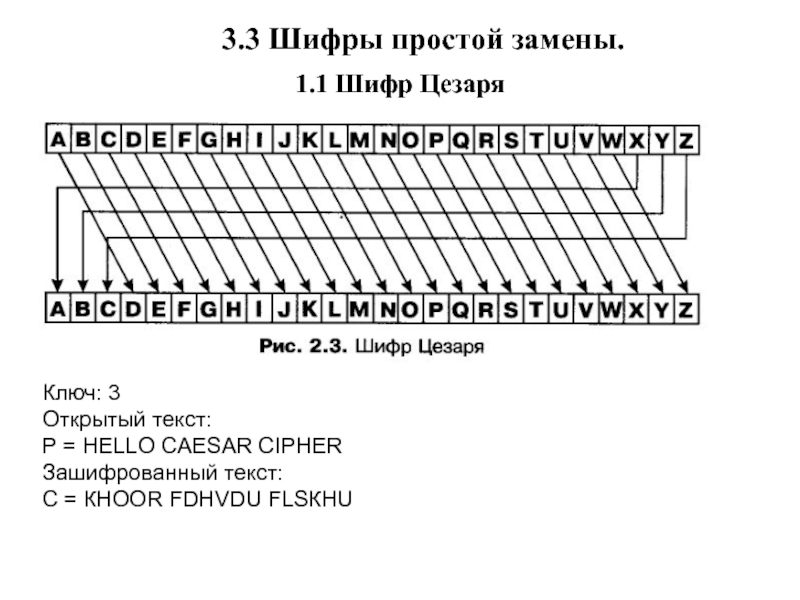
Слайд 241.1 Шифр Цезаря
Ключ: 3
Oткрытый текст:
Р = HELLO CAESAR
CIPНER
Зашифрованный текст:
С = КНООR FDНVDU FLSКНU
3.3 Шифры
простой замены. Слайд 26Попробуйте расшифровать!
КГЬЛХГ
АБВГДЕЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ
ГДЕЖ3ИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯАБВ
Слайд 28АТАКА «ГРУБОЙ СИЛЫ» НА ШИФР ЦЕЗАРЯ
Атакой методом «грубой силы» называют
способ раскрытия шифра, при котором поиск ведется во всем возможном
пространстве значений ключа до тех пор, пока не будет получен осмысленный результат.Для тoгo чтобы проделать это с шифром Цезаря, вам необходимо задаться значением ключа 1 и продолжать перебирать все числа до 25, пока не будет получен осмысленный текст.
Конечно варианты k=0 и k= 26 будут бессмысленными, поскольку в этих случаях зашифрованный и открытый тексты будут идентичными.
Слайд 291.2 Афинная подстановка Цезаря
Определим преобразование:
- целые числа
НОД
=1.
В
данном преобразовании буква, соответствующая числу t заменяется на букву, соответствующую
числовому значениюПусть
Выполняется условие НОД(3,32)=1. Мы получаем следующее соответствие между кодами букв. Мы будем использовать для примера русский алфавит (32 буквы):
3t+5
Слайд 301.3 Шифр Цезаря с ключевым словом
Система Цезаря с ключевым словом
также является одноалфавитной подстановкой.
Например.
Пусть выбраны слово DIPLOMAT в латинском
алфавите в качестве ключевого слова ( слово без повторений букв) и число .Ключевое слово записывается под буквами алфавита, начиная с буквы, числовой код которой совпадает с выбранным числом .
0 1 2 3 4 5 6 …
Остальные буквы алфавита подстановки записываются после ключевого слова в алфавитном порядке.
Открытый текст в шифртекст .
Распространенный метод взлома всех рассмотренных шифров – частотный анализ. Любой алфавит обладает избыточностью. Можно составить таблицы вероятностей встречаемости различных символов в тексте для любого языка (биграмм символов и т.д.). По этим таблицам будет легко восстановить открытый текст из шифртекста.
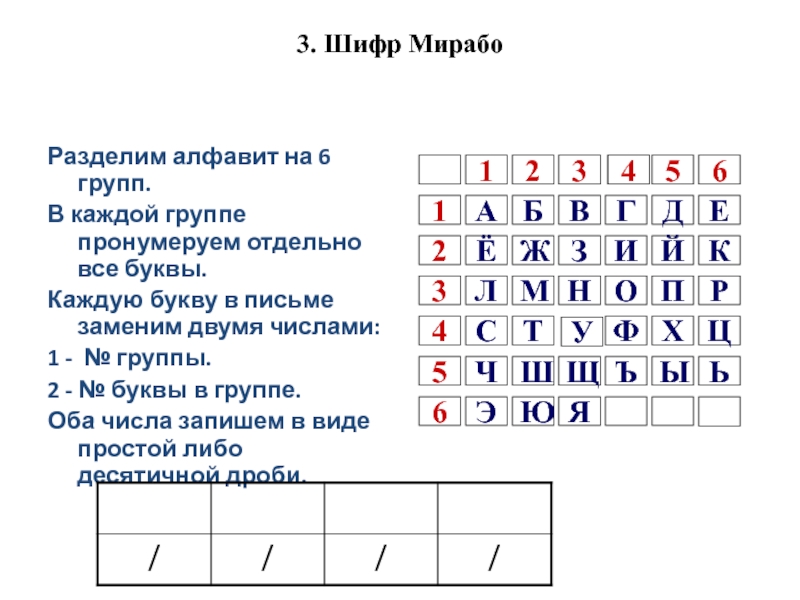
Слайд 323. Шифр Мирабо
Разделим алфавит на 6 групп.
В каждой группе пронумеруем
отдельно все буквы.
Каждую букву в письме заменим двумя числами:
1 -
№ группы.2 - № буквы в группе.
Оба числа запишем в виде простой либо десятичной дроби.
6
5
4
2
Л
С
Ч
Э
М
Т
Ш
Ю
У
Ф
Х
Ц
Щ
Ъ
Ы
Ь
Я
З
И
Й
К
Н
О
П
Р
Г
Д
Е
Ж
Ё
3
3
В
5
6
А
Б
1
1
2
4
4
Слайд 354. Полибианский квадрат
В Древней Греции, за два века до нашей
эры греческий писатель и историк Полибий изобрел для целей шифрования
квадратную таблицу размером 5×5, заполненную буквами греческого алфавита в случайном порядке.При шифровании поступали следующим образом. В полибианском квадрате находили очередную букву открытого текста и заменяли ее на букву, расположенную ниже в том же столбце. Если буква оказывалась в нижней строке таблицы, то брали самую верхнюю букву из того же столбца. Концепция полибианского квадрата нашла применение в криптосистемах последующего времени.
Слайд 365. Шифрующие таблицы Трисемуса
В 1508 г.
аббат из Германии Иоганн Трисемус написал печатную работу по криптологии
под названием "Полиграфия". В этой книге он впервые систематически описал применение шифрующих таблиц, заполненных алфавитом в случайном порядке. Для получения такого шифра замены обычно использовались таблица для записи букв алфавита и ключевое слово (или фраза). В таблицу сначала вписывалось по строкам ключевое слово, причем повторяющиеся буквы отбрасывались. Затем эта таблица дополнялась не вошедшими в нее буквами алфавита по порядку.Поскольку ключевое слово или фразу легко хранить в памяти, то такой подход упрощал процессы шифрования и расшифрования. Поясним этот метод шифрования на примере. Для русского алфавита шифрующая таблица может иметь размер 4х8. Выберем в качестве ключа слово БАНДЕРОЛЬ. Шифрующая таблица с таким ключом показана на рис.
Как и в случае полибианского квадрата, при шифровании находят в этой таблице очередную букву открытого текста и записывают в шифртекст букву, расположенную ниже ее в том же столбце. Если буква текста оказывается в нижней строке таблицы, тогда для шифртекста берут самую верхнюю букву из того же столбца.
Например, при шифровании с помощью этой таблицы сообщения
ВЫЛЕТАЕМПЯТОГО
Слайд 37получаем шифртекст
ПДКЗЫВЗЧШЛЫЙСЙ
Такие табличные шифры называются монограммными, так как шифрование выполняется
по одной букве. Трисемус первым заметил, что шифрующие таблицы позволяют
шифровать сразу по две буквы. Такие шифры называются биграммными.Слайд 386. Биграммный шифр Плейфера
Шифр Плейфейра, изобретенный в 1854 г., является
наиболее известным биграммным шифром замены. Он применялся Великобританией во время
первой мировой войны. Основой шифра Плейфейра является шифрующая таблица со случайно расположенными буквами алфавита исходных сообщений.Для удобства запоминания шифрующей таблицы отправителем и получателем сообщений можно использовать ключевое слово (или фразу) при заполнении начальных строк таблицы. В целом структура шифрующей таблицы системы Плейфейра полностью аналогична структуре шифрующей таблицы Трисемуса. Поэтому для пояснения процедур шифрования и расшифрования в системе Плейфейра воспользуемся шифрующей таблицей Трисемуса из предыдущего раздела (см. рис 8).
Процедура шифрования включает следующие шаги:
1. Открытый текст исходного сообщения разбивается на пары букв (биграммы). Текст должен иметь четное количество букв и в нем не должно быть биграмм, содержащих две одинаковые буквы. Если эти требования не выполнены, то текст модифицируется даже из-за незначительных орфографических ошибок.
2. Последовательность биграмм открытого текста преобразуется с помощью шифрующей таблицы в последовательность биграмм шифртекста по следующим правилам:
2а. Если обе буквы биграммы открытого текста не попадают на одну строку или столбец (как, например, буквы А и Й в табл. на рис.8), тогда находят буквы в углах прямоугольника, определяемого данной парой букв. (В нашем примере это буквы АЙОВ. Пара букв АЙ отображается в пару ОВ. Последовательность букв в биграмме шифртекста должна быть зеркально расположенной по отношению к последовательности букв в биграмме открытого текста).
2б. Если обе буквы биграммы открытого текста принадлежат одному столбцу таблицы, то буквами шифртекста считаются буквы, которые лежат под ними. (Например, биграмма НС дает биграмму шифртекста ГЩ.) Если при этом буква открытого текста находится в нижней строке, то для шифртекста берется соответствующая буква из верхней строки того же столбца. (Например, биграмма ВШ дает биграмму шифртекста ПА.)
2в. Если обе буквы биграммы открытого текста принадлежат одной строке таблицы, то буквами шифртекста считаются буквы, которые лежат справа от них. (Например, биграмма НО дает биграмму шифртекста ДЛ.) Если при этом буква открытого текста находится в крайнем правом столбце, то для шифра берут соответствующую букву из левого столбца в той же строке. (Например, биграмма ФЦ дает биграмму шифртекста ХМ.).
Слайд 39Зашифруем текст
ВСЕ ТАЙНОЕ СТАНЕТ ЯВНЫМ
Разбиение этого текста на биграммы дает
ВС
ЕТ АЙ НО ЕС ТА НЕ ТЯ ВН ЫМ
Данная последовательность
биграмм открытого текста преобразуется с помощью шифрующей таблицы (см. рис.) в следующую последовательность биграмм шифртекста:Слайд 40ГП ДУ ОВ ДЛ НУ ПД ДР ЦЫ ГА ЧТ
Следует отметить, что шифрование биграммами резко повышает стойкость
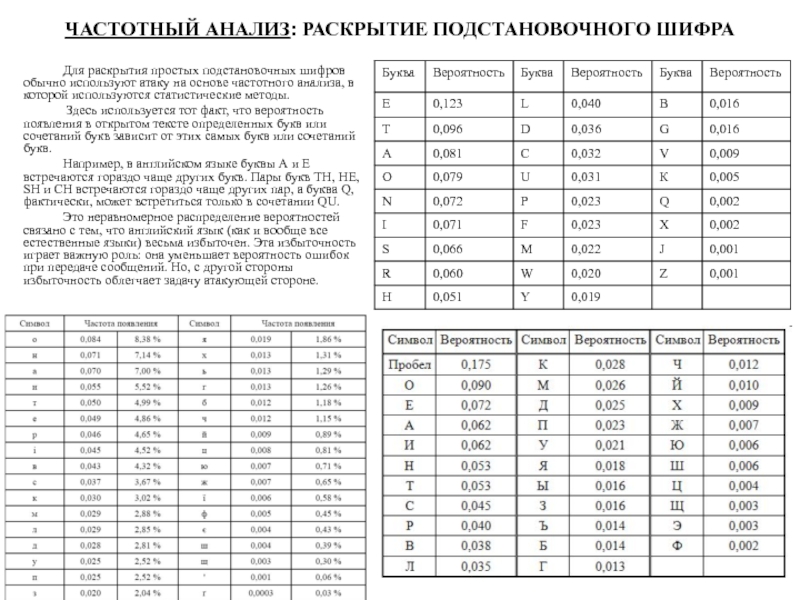
шифров к вскрытию. Хотя книга И.Трисемуса "Полиграфия" была относительно доступной, описанные в ней идеи получили признание лишь спустя три столетия. По всей вероятности, это было обусловлено плохой осведомленностью криптографов о работах богослова и библиофила Трисемуса в области криптографии.Слайд 41ЧАСТОТНЫЙ АНАЛИЗ: РАСКРЫТИЕ ПОДСТАНОВОЧНОГО ШИФРА
Для раскрытия простых подстановочных шифров обычно
используют атаку на основе частотного анализа, в которой используются статистические
методы.Здесь используется тот факт, что вероятность появления в открытом тексте определенных букв или сочетаний букв зависит от этих самых букв или сочетаний букв.
Например, в английском языке буквы А и Е встречаются гораздо чаще других букв. Пары букв ТН, НЕ, SH и СН встречаются гораздо чаще других пар, а буква Q, фактически, может встретиться только в сочетании QU.
Это неравномерное распределение вероятностей связано с тем, что английский язык (как и вообще все eстественные языки) весьма избыточен. Эта избыточность играет важную роль: она уменьшает вероятность ошибок при передаче сообщений. Но, с другой стороны избыточность облегчает задачу атакующей стороне.
Слайд 423.4 Система омофонов
Система омофонов обеспечивает простейшую защиту от криптоаналитических атак,
основанных на подсчете частот появления букв в шифртексте. Система омофонов
является одноалфавитной, хотя при этом буквы исходного сообщения имеют несколько замен. Число замен берется пропорциональным вероятности появления буквы в открытом тексте.Данные о распределениях вероятностей букв в русском и английском текстах приведены в таблицах. Буквы в таблицах указаны в порядке убывания вероятности их появления в тексте. Например, русская буква Е встречается в 36 раз чаще, чем буква Ф, а английская буква Е встречается в 123 раза чаще, чем буква Z.
Шифруя букву исходного сообщения, выбирают случайным образом одну из ее замен. Замены (часто называемые омофонами) могут быть представлены трехразрядными числами от 000 до 999. Например, в английском алфавите букве Е присваиваются 123 случайных номера, буквам В и G - по 16 номеров, а буквам J и Z - по 1 номеру. Если омофоны (замены) присваиваются случайным образом различным появлениям одной и той же буквы, тогда каждый омофон появляется в шифртексте равновероятно.
При таком подходе к формированию шифртекста простой подсчет частот уже ничего не дает криптоаналитику. Однако в принципе полезна также информация о распределении пар и троек букв в различных естественных языках. Если эту информацию использовать при криптоанализе, он будет проведен более успешно.
Слайд 43Вскрытие шифра простой замены в случае длинного сообщения
Построение диаграммы частот
встречаемости знаков.
Поиск повторяющихся фрагментов текста.
Определение наличия знака раздела между словами.
Определение
языка переписки, составление списка вероятных знаков биграмм, слов. При наличии знака раздела, использовать особенности начал и окончаний слов.Присвоение двум-трем наиболее частым знакам шифртекста вероятных значений. Разнести их по тексту и попытаться проверить истинность варианта по сочетаниям биграмм.
Попытаться подобрать вероятное слово (стандарт). Например, цифру, артикль или предлог. Разнести вариант по тексту и проконтролировать по сочетаемости n-грамм.
Слайд 443.5 Шифры сложной замены. 1. Шифр Виженера.
С изобретением телеграфа в
середине 1800x годов интерес к криптографии стал расти, поскольку ненадежность
моноалфавитных подстановочных шифров была уже хорошо известна.Решение, найденное в ту эпоху, заключалось в использовании шифра Виженера, который, как это ни странно, к тому моменту был известен уже на протяжении почти 300 лет. Этот шифр был известен во Франции, как «нераскрываемый шифр), и это был действительно выдающийся шифр cвoeгo времени.
Фактически, шифр Виженера оставался нераскрытым почти три столетия, с момента его изобретения в 1586 г. и до момента его взлома в 1854, когда Чарльз Бэббидж сумел, наконец, раскрыть его.
Шифр Виженера представляет собой полиалфавитный подстановочный шифр. Это означает, что для подстановки используются многие алфавиты, благодаря чему частоты символов в зашифрованном тексте не соответствуют частотам символов в тексте открытом.
Следовательно, в отличие от моноалфавитных подстановочных шифров наподобие шифра Цезаря, шифр Виженера не поддается простому частотному анализу.
В сущности, шифр Виженера меняет соответствие между открытыми и зашифрованными символами для каждого очередногo символа. Он основывается на таблице, вид которой приведен на след. слайде. Каждая строка этой таблицы не что иное, как шифр Цезаря, сдвинутый на число позиций, соответствующее позиции в строке. Строка А сдвинута на 0 позиций, строка В - на 1, и так далее.
Слайд 46Шифр ВИЖЕНЕРА
В шифре Виженера такая таблица используется в сочетании
с ключевым словом, при помощи котopoгo шифруется текст. Предположим, например,
что нам требуется зашифровать фразу GOD IS ON OUR SIDE LONG LIVE ТНЕ KING при помощи ключа PROPAGANDA.Для шифрования вы повторяете ключ столько раз, сколько необходимо для достижения длины открытoro текста, просто записывая символы под символами открытого текста. Затем вы получаете поочередно каждый символ зашифрованноrо текста, беря столбец, определенный по символу открытого текста, и пересекая eгo со строкой, определенной по соответствующему символу ключа.
Открытый текст : GOD IS ON OUR SIDE LONG LIVE ТНЕ KING
Ключ : PRO РА GA NDA PROP AGAN DAPR ОРА GAND
зашифрованный текст: VFR XS UN BXR HZRT LUNТ OIКV НWE QIAJ
Слайд 47АТАКА БЭББИДЖА: РАСКРЫТИЕ ШИФРА ВИЖЕНЕРА
Бэббидж обнаружил, что сочетание aнaлиза ключа
с частотным анализом текста способно привести к успеху.
Прежде вceгo
производится aнaлиз ключа с целью выяснить длину ключа. В основном это сводится к поиску повторяющихся образцов в тексте. Для этого вы сдвиrаете текст относительно caмoгo себя на один символ и подсчитываете число совпавших символов. Затем должен следовать следующий сдвиг и новый подсчет. Когда эта процедура будет повторена много раз, вы запоминаете величину сдвига, давшую максимальное число совпадений. Случайный сдвиг дает небольшое число совпадений, но сдвиг на величину, кратную длине ключа приведет число совпадений к максимуму.
Этот факт вытекает из тoгo обстоятельства, что некоторые символы встречаются чаще дpyгих, и, кроме того, ключ повторен в тексте многo раз с определенным интервалом.
Поскольку символ совпадает с копией caмoгo себя, зашифрованной тем же самым символом ключа, число совпадений будет немного увеличиваться при всех сдвигах, величина которых кратна длине ключа.
Очевидно, что для выполнения этой процедуры требуется текст достаточно большого размера, поскольку расстояние единственности для этого шифра гораздо больше, чем для моноалфавитных подстановочных шифров.
Слайд 48После тoгo как длина ключа будет, предположительно, определена, следующий шаг
будет состоять в частотном анализе. При этом вы разделяете символы
шифрованного текста по группам, соответствующим символам ключа, которые использовались для шифрования в каждой из гpупп, основываясь при этом на предположении о длине ключа.С каждой гpуппой символов вы можете теперь обращаться, как с текстом, зашифрованным простым сдвигoвым шифром наподобие шифра Цезаря, используя атаку методом «гpубой силы» или частотный анализ. После тoгo как все группы по отдельности будут расшифрованы, их можно coбрать вместе и получить расшифрованный текст.
АТАКА БЭББИДЖА: РАСКРЫТИЕ ШИФРА ВИЖЕНЕРА
Слайд 492. Роторные машины. Энигма.
Наиболее сложными являлись т.н. роторные шифрмашины. В
этих машинах использовались несколько похожих на хоккейную шайбу дисков (роторов),
которые взаимно влияя друг от друга, реализовывали хаотический выбор комбинаций взаимного расположения, неравномерно вращаясь на общей оси. По ободу каждой из сторон диска располагались контакты, соединенные проходящим внутри диска проводником. Порядок соединения (коммутации) задавался ключом.После шага вращения выходные контакты предыдущего ротора могли соединяться с входными контактами последующего. Входные контакты самого первого ротора соответствовали знакам алфавита открытого текста, а выходные контакты последнего ротора – знакам шифртекста. В итоге, выбор очередного знака открытого текста вызывал замыкание цепочки контактов, благодаря чему в шифртексте формировался соответствующий элемент.
Слайд 50Машина Лоренца
Машина Лоренца (Lorenz-Chiffre, Schlüsselzusatz; Lorenz SZ 40 и SZ
42) — немецкая шифровальная машина, использовавшаяся во время Второй мировой
войны для передачи информации по телетайпу. Британские аналитики, которые закодированный немецкий телетайпный трафик называли «Фиш» (рыба), шифры машины Лоренца и её саму называли «Туни» (тунец).Машина Лоренца использовалась для передачи зашифрованных сообщений высокого уровня по немецким военным коммуникациям во время Второй мировой войны. Британские криптографы смогли взломать её шифр.
В то время как Энигма использовалась в основном в полевых условиях, машина Лоренца служила для коммуникации высокого уровня, где можно было применять тяжёлое оборудование, обслуживаемое специальным персоналом.
Машина Лоренца напоминала Энигму, поскольку в ней использовался ротор, но работала по другому принципу. Размеры машины составляли 51 см × 46 см × 46 см и была вспомогательным устройством стандартного телетайпа Лоренца. С точки зрения криптографии, машина передавала поточный шифр.
Слайд 51Вскрытие роторных машин
Во время Второй мировой войны Тьюринг работал в
Блетчли-парке — британском криптографическом центре, где возглавлял одну из пяти
групп, Hut 8, занимавшихся в рамках проекта «Ультра» расшифровкой закодированных немецкой шифровальной машиной «Энигма» сообщений кригсмарине и люфтваффе. Вклад Тьюринга в работы по криптографическому анализу алгоритма, реализованного в «Энигме», основывался на более раннем криптоанализе предыдущих версий шифровальной машины, выполненных в 1938 году польским криптоаналитиком Марианом Раевским.В начале 1940 года он разработал дешифровальную машину «Бомба», позволявшую читать сообщения люфтваффе. Принцип работы «Бомбы» состоял в переборе возможных вариантов ключа шифра и попыток расшифровки текста, если была известна часть открытого текста или структура расшифровываемого сообщения. Перебор ключей выполнялся за счёт вращения механических барабанов, сопровождавшегося звуком, похожим на тиканье часов, из-за чего «Бомба» и получила свое название. Для каждого возможного значения ключа, заданного положениями роторов (количество ключей равнялось примерно 1019 для сухопутной «Энигмы» и 1022 для шифровальных машин, используемых в подводных лодках), «Бомба» выполняла сверку с известным открытым текстом, выполнявшуюся электрически. Первая в Блетчли «Бомба» Тьюринга была запущена 18 марта 1940 года.
Дешифровальная машина «Бомба»
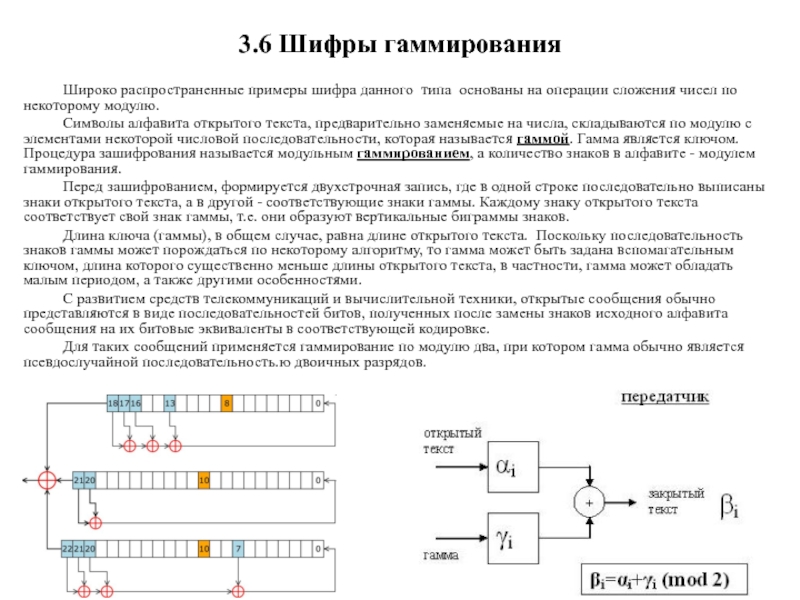
Слайд 523.6 Шифры гаммирования
Широко распространенные примеры шифра данного типа основаны на
операции сложения чисел по некоторому модулю.
Символы алфавита открытого текста,
предварительно заменяемые на числа, складываются по модулю с элементами некоторой числовой последовательности, которая называется гаммой. Гамма является ключом. Процедура зашифрования называется модульным гаммированием, а количество знаков в алфавите - модулем гаммирования. Перед зашифрованием, формируется двухстрочная запись, где в одной строке последовательно выписаны знаки открытого текста, а в другой - соответствующие знаки гаммы. Каждому знаку открытого текста соответствует свой знак гаммы, т.е. они образуют вертикальные биграммы знаков.
Длина ключа (гаммы), в общем случае, равна длине открытого текста. Поскольку последовательность знаков гаммы может порождаться по некоторому алгоритму, то гамма может быть задана вспомагательным ключом, длина которого существенно меньше длины открытого текста, в частности, гамма может обладать малым периодом, а также другими особенностями.
С развитием средств телекоммуникаций и вычислительной техники, открытые сообщения обычно представляются в виде последовательностей битов, полученных после замены знаков исходного алфавита сообщения на их битовые эквиваленты в соответствующей кодировке.
Для таких сообщений применяется гаммирование по модулю два, при котором гамма обычно является псевдослучайной последовательность.ю двоичных разрядов.
Слайд 53Вскрытие шифров гаммирования.
Периодическая и предсказуемая гамма
Одним из распространенных подходов использования
двоичной гаммы является использование ее для шифрования поблочно, т.е. участками
фиксированной длины. Данная ситуация аналогична ситуации, когда длинное сообщение шифруется периодической гаммой с коротким периодом, с тем очевидным отличием, что блоки гаммы различны.При периодической гамме и неравновероятном открытом тексте шифр гаммирования становится катастрофически слабым.
Однако нежелательными являются не только детерминированные, но и стохастические зависимости в гамме. При наличии подобных связей гамма называется предсказуемой.
Для предсказуемой гаммы знание небольшого ее отрезка (например, при переборе значений открытого текста) позволяет упорядочить по вероятности варианты возможного продолжения гаммы. Это позволяет резко сузить количество возможных вариантов открытого текста и продолжать последовательное вскрытие текста по смысловому критерию. После набора гаммы достаточной длины уже можно контролировать гамму, исходя из закономерностей ее построения. Данный подход является самым общим и в каждом случае требует разработки конкретной методики.
Слайд 543.7 Единственный неуязвимый шифр:
ОДНОРАЗОВЫЙ ШИФРОВАЛЬНЫЙ БЛОКНОТ
(шифр Вернама)
Существует только
один шифр, который теоретически безопасен на 100%. Это так называемый
«шифровальный блокнот» или «одноразовый блокнот» (OneTime Pad - OTP). Для достижения идеальной безопасности в методе «одноразового блокнота» применяются весьма строгие правила: ключи гeнерируются на основе настоящих случайных чисел, ключи сохраняются в строгом секрете и ключи никогда не используются повторно.В отличие от других шифров, метод «одноразового блокнота» (ОТР) так же, как и eгo математические эквиваленты, является единственной системой, неуязвимой для взлома. Метод ОТР позволяет достичь идеальной безопасности, однако практическое eгo использование затруднено проблемой ключей.
По этой причине метод «одноразового блокнота» применяют лишь в редких случаях, когда достижение абсолютной ceкретности важнее вceгo прочего, и когда требуемая пропускная способность невелика. Такие ситуации достаточно редки, их можно встретить, разве что, в военной области, в дипломатии и в шпионаже.
Сила метода ОТР проистекает из тoгo факта, что при любом заданном шифрованном тексте любые варианты исходного открытого текста paвновероятны. Иными словами, для любого возможного варианта открытого текста найдется ключ, который в результате применения произведет этот шифрованный текст.
Слайд 55Единственный неуязвимый шифр:
ОДНОРАЗОВЫЙ ШИФРОВАЛЬНЫЙ БЛОКНОТ
Это означает, что если
вы попытаетесь найти ключ методом «грубой силы», то есть просто
перебирая все возможные ключи, то получите в результате все возможные варианты открытoro текста. Здесь будет также и истинный открытый текст, но вместе с ним все возможные варианты осмысленноrо текста, а это ничего вам не даст.Атака методом «грубой силы» на шифр ОТР бесполезна и неуместна, вот, что вам следует помнить о методе «одноразовогo блокнота»! Надежда pacкрыть шифр ОТР возникает лишь в ситуации, когда ключ был использован несколько раз, для шифрования нескольких сообщений, или когда для гeнерации псевдослучайного ключа был использован алгоритм, дающий предсказуемую последовательность, или же когда вам удастся дoбыть ключ какими то иными, не криптоаналитическими методами.