Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математический анализ
Содержание
- 1. Математический анализ
- 2. ПРОГРАММА ПЕРВОГО СЕМЕСТРАРаздел 1. Введение в
- 3. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРАТер-Крикоров А.М., Шабунин М.И. Курс математического
- 4. Раздел 1. ВВЕДЕНИЕ В АНАЛИЗ.
- 5. Лекция 1.1.Предмет математического анализа, его роль в
- 6. Предмет математического анализа. Математический анализ – обширный
- 7. Историческая справка Начиная с математиков Древней Греции
- 8. Ньютон (Newton) Исаак (1643 – 1727)
- 9. Лейбниц (Leibniz) Готфрид Вильгельм (1646-1716)Выдающийся немецкий математик,
- 10. Эйлер (Euler) Леонард (1707 - 1783)
- 11. Лагранж (Lagrange) Жозеф Луи (1736-1813)Выдающийся французский математик
- 12. Коши (Cauchy) Огюстен Луи (1789
- 13. Символы математической логики
- 14. Множества. Операции над множествами.
- 15. Числовые множества. Напомним обозначения некоторых известных числовых
- 16. .Отрезок [a, b] = {x: a ≤
- 17. .Окрестности точек на числовой прямой- ε-окрестность точки
- 18. Некоторые свойства модуля вещественного числа. Для любого
- 19. Ограниченные и неограниченные множества Множество Х⊂ R называется
- 20. Определение точной верхней и нижней грани Наименьшая из
- 21. ПРИМЕРЫ. 1) Х =
- 22. Числовые функции Понятие числовой функции действительной переменной Если
- 23. График функции Графиком функции y = f(x), х∈Х
- 24. Слайд 24
- 25. Четные и нечетные функции Функция f(x) определенная на
- 26. Периодические функции Функция f(x) определенная на множестве
- 27. Монотонные функции Функция f(x) называется возрастающей (строго возрастающей)
- 28. Обратная функция D(f) = [a, b] – область
- 29. Отметим следующие свойства, показывающие, как связаны данная
- 30. Спасибо за внимание!
- 31. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Математический анализ
Поток ММ
лектор
Профессор, доктор физико-математических наук,
Заслуженный деятель науки
РФ
Слайд 2ПРОГРАММА
ПЕРВОГО СЕМЕСТРА
Раздел 1. Введение в анализ.
Раздел 2. Предел функции.
Непрерывность функций одной переменной.
Раздел 3. Дифференциальное исчисление функций одной
переменной.Раздел 4. Дифференциальное исчисление функций нескольких переменных.
Слайд 3РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Тер-Крикоров А.М., Шабунин М.И. Курс математического анализа.– М.: Физматлит,
2003.
Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. – М.:
Наука, 1969. – Т. 1. Кудрявцев Л.Д. Курс математического анализа. – М.: Высшая школа, 1981. – Т. 1.
Сборник задач по математике для втузов. Под редакцией А.В.Ефимова и Б.П.Демидовича. Часть 1. Линейная алгебра и основы математического анализа.
Кузнецов Л.А. Сборник заданий по высшей математике.
Слайд 5Лекция 1.1.
Предмет математического анализа, его роль в изучении и создании
математических моделей.
Математическая символика.
Числовые множества.
Ограниченные и неограниченные множества. Точные
грани числового множества. Теорема существования точной грани ограниченного множества.Числовые функции
Слайд 6Предмет математического анализа.
Математический анализ – обширный раздел математики, в котором
функции и их обобщения изучаются методом пределов. Понятие предела тесно
связано с понятием бесконечно малой величины, поэтому можно также сказать, что математический анализ изучает функции и их обобщения методом бесконечно малых.В природе и технике всюду встречаются движения, процессы, которые описываются функциями; законы явлений природы также обычно описываются функциями. Отсюда объективная важность математического анализа как средства изучения функций.
Основы математического анализа включают в себя теорию действительного числа, теорию пределов, дифференциальное и интегральное исчисление и их приложения, теорию рядов.
Начиная с математиков Древней Греции и вплоть до
Слайд 7Историческая справка
Начиная с математиков Древней Греции и вплоть до
Начиная с трудов математиков Древней Греции
и вплоть до 17 века математический анализ представлял собой совокупность решений разрозненных частных задач; например, в интегральном исчислении проводилось вычисление площадей различных фигур и объемов тел с кривыми границами, вычисление работы переменной силы и т. д. Каждая такая задача решалась сложным и громоздким методом исчерпывания. Математический анализ как единое и систематическое целое сложился в трудах И.Ньютона (I.Newton), Г.Лейбница (G.Leibniz), Л.Эйлера (L.Euler), Ж.Лагранжа (J.Lagrange) и других ученых 17-18 века, а его современная база – теория пределов – была разработана О.Коши (A.Cauchy) лишь в начале 19 века.Слайд 8Ньютон (Newton) Исаак
(1643 – 1727)
Великий английский математик, механик,
астроном и физик, президент Лондонского королевского общества с 1703 г.
Разработал
(независимо от Г. Лейбница) дифференциальное и интегральное исчисления.Слайд 9Лейбниц (Leibniz) Готфрид Вильгельм
(1646-1716)
Выдающийся немецкий математик, физик, языковед и философ-идеалист
. Основатель и президент Берлинского научного общества.
По просьбе Петра I
разработал проекты развития образования и государственного управления в России.Создатель теории нестандартного дифференциального и интегрального исчисления.
Слайд 10Эйлер (Euler) Леонард
(1707 - 1783)
Великий швейцарский, российский и
немецкий математик, механик, физик и астроном. Не найдя в Швейцарии
условий для научной деятельности, переехал в 1727 году в Россию. С 1766 академик Петербургской АН. В период политической неустойчивости России, когда наукой пренебрегали перешел на работу в Германию. Вернулся в Россию по приглашению Екатерины Второй.Автор свыше 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближенным вычислениям, небесной механике и гидромеханике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др., оказавших решающее влияние на развитие всех этих и многих других областей науки.
Слайд 11Лагранж (Lagrange) Жозеф Луи
(1736-1813)
Выдающийся французский математик и механик, президент Берлинской
АН, иностранный почетный член Петербургской АН.
Основополагающие труды по математическому анализу,
теории чисел, алгебре,дифференциальным уравнениям и вариационному исчислению, .
Слайд 12
Коши (Cauchy) Огюстен Луи
(1789 – 1857)
Выдающийся французский математик,
иностранный почетный член Петербургской АН (1831).
Разработал базу математического анализа
– теорию пределов.Один из создателей теории обыкновенных дифференциальных уравнений и теории функций комплексного переменного.
Слайд 15Числовые множества.
Напомним обозначения некоторых известных числовых множеств:
N = {1,
2, 3, …} – множество натуральных чисел,
Z = {0, ±1,
±2, …} – множество целых чисел,Q ={p/q, p∈ Z, q∈ N} – множество рациональных чисел,
(состоит из бесконечных периодических десятичных дробей)
J – множество иррациональных чисел (состоит из бесконечных непериодических десятичных дробей),
R = Q ∪ J – множество действительных (вещественных) чисел.
Слайд 16.
Отрезок [a, b] = {x: a ≤ x ≤ b}
Интервал (a, b) = {x: a < x < b}
Полуинтервалы [a, b) = {x: a ≤ x < b}, (a, b] = {x: a < x ≤ b}
Бесконечные интервалы (открытые полуоси)
(a, + ∞) = {x: x > a}, (- ∞, b) = {x: x < b}
Бесконечные полуинтервалы (полуоси)
[a, + ∞) = {x: x ≥ a}, (- ∞, b] = {x: x ≤ b}
Промежутки на числовой оси
Слайд 17.
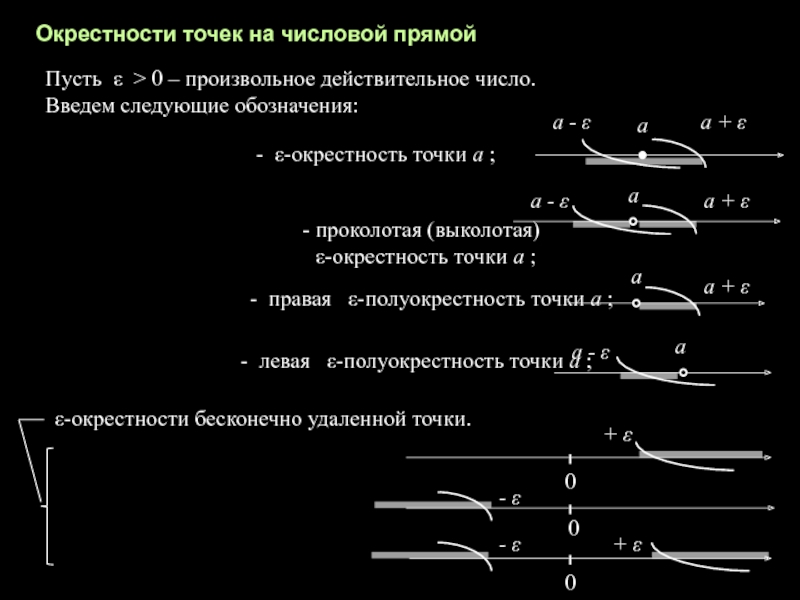
Окрестности точек на числовой прямой
- ε-окрестность точки а ;
проколотая
(выколотая)
ε-окрестность точки а ;
- правая ε-полуокрестность точки
а ;- левая ε-полуокрестность точки а ;
Пусть ε > 0 – произвольное действительное число.
Введем следующие обозначения:
a
a - ε
a + ε
a
a
a
a - ε
a - ε
a + ε
a + ε
- ε
- ε
+ ε
+ ε
0
0
0
ε-окрестности бесконечно удаленной точки.
Слайд 18Некоторые свойства модуля вещественного числа.
Для любого вещественного числа а число
называется абсолютной величиной числа а или модулем.
Неравенство ⎜а ⎜≤ δ
эквивалентно неравенствам –δ ≤ а ≤ δ .Неравенство ⎜а ⎜> δ эквивалентно совокупности неравенств
Перечислим без доказательства основные свойства модуля:
⎜– а ⎜= ⎜а ⎜;
⎜аb ⎜= ⎜а ⎜⋅ ⎜b ⎜;
⎜а ± b ⎜≤ ⎜а ⎜+⎜b ⎜;
⎜⎜а ⎜– ⎜ b ⎜⎜≤ ⎜а – b ⎜.
Слайд 19Ограниченные и неограниченные множества
Множество Х⊂ R называется ограниченным снизу, если
существует число С1∈R такое, что для всех х∈Х выполняется неравенство
С1≤ x. Число С1 называется нижней гранью множества Х.Множество Х⊂ R называется ограниченным сверху, если существует число С2∈R, такое что для всех х∈Х выполняется неравенство x ≤ С2. Число С2 называется верхней гранью множества Х.
Множество, ограниченное сверху и снизу, называется ограниченным множеством.
Последнее определение эквивалентно следующему:
Множество Х⊂ R ограничено ⇔ ∃С > 0 : ∀х∈Х → ⎢х ⎢≤ С.
Определение неограниченного множества можно сформулировать как отрицание последнего:
Множество Х⊂ R неограничено, если ∀ С > 0 ∃х∈Х: ⎢х ⎢ > С.
Слайд 20Определение точной верхней и нижней грани
Наименьшая из верхних граней множества
Х⊂ R называется его точной верхней гранью и обозначается через
supX или(читается «супремум»).
Определение 1. Число М = supX, если:
1) ∀х ∈ Х → x ≤ М;
2) ∀ε >0 ∃ хε∈ Х : М - ε < хε < М.
Наибольшая из нижних граней множества Х⊂ R называется его точной нижней гранью и обозначается через inf X или
(читается «инфимум»).
Определение 2. Число m = inf X, если:
1) ∀х ∈ Х → x ≥ m;
2) ∀ ε >0 ∃ хε ∈ Х : m < хε < m + ε.
М
М - ε
ε
хε
X
хε
X
ε
m + ε
m
(т.е. М – верхняя грань Х)
(т.е. М – наименьшая их верхних граней Х)
х
х
(т.е. m – нижняя грань Х)
(т.е. m – наибольшая их нижних граней Х)
Слайд 21ПРИМЕРЫ.
1) Х = (0, 1)
supX =
1∉ Х, inf X = 0 ∉ Х;
2) Х =
(0, 1] supX = 1∈ Х, inf X = 0 ∉ Х;
3) Х = (0, 1)∪{2}
supX = 2 ∈ Х.
АКСИОМА СУЩЕСТВОВАНИЯ ТОЧНОЙ ВЕРХНЕЙ ГРАНИ.
К известным из школы свойствам вещественных чисел добавим следующее: У всякого непустого, ограниченного сверху множества существует его точная верхняя грань.
Отсюда имеем: У всякого непустого, ограниченного снизу множества существует его точная нижняя грань.
х
х
х
1
1
1
2
0
0
0
X
X
X
Слайд 22Числовые функции
Понятие числовой функции действительной переменной
Если каждому х ∈Х
⊂ R поставлено в соответствие по некоторому правилу единственное y
∈Y ⊂ R, то говорят, что на множестве Х определена числовая функция действительной переменной х.Правило, устанавливающее соответствие, обозначают некоторым символом, например f, и пишут
y = f(x), х ∈ Х.
Множество X называют областью определения функции и обозначают D(f). Множество Y называют множеством значений функции и обозначают Е(f).
Для обозначения функции используют также запись вида
f: X→Y.
Слайд 23 График функции
Графиком функции y = f(x), х∈Х в прямоугольной системе
координат называется множество всех точек плоскости с координатами (х, f(x)).
ПРИМЕР
y = signx = График функции иногда можно получить преобразованием известного графика другой функции f(x), как показано в таблице:
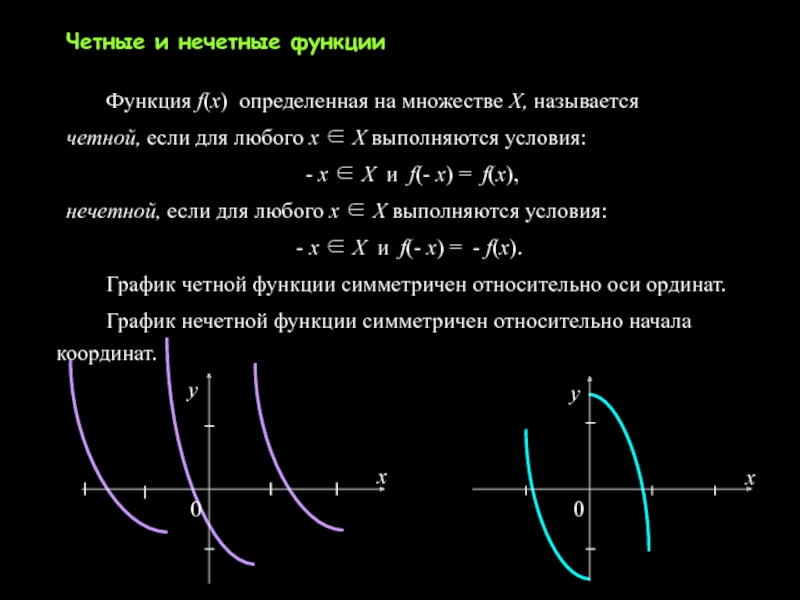
Слайд 25 Четные и нечетные функции
Функция f(x) определенная на множестве X, называется
четной, если для любого x ∈ X выполняются условия:
-
x ∈ X и f(- x) = f(x),нечетной, если для любого x ∈ X выполняются условия:
- x ∈ X и f(- x) = - f(x).
График четной функции симметричен относительно оси ординат.
График нечетной функции симметричен относительно начала координат.
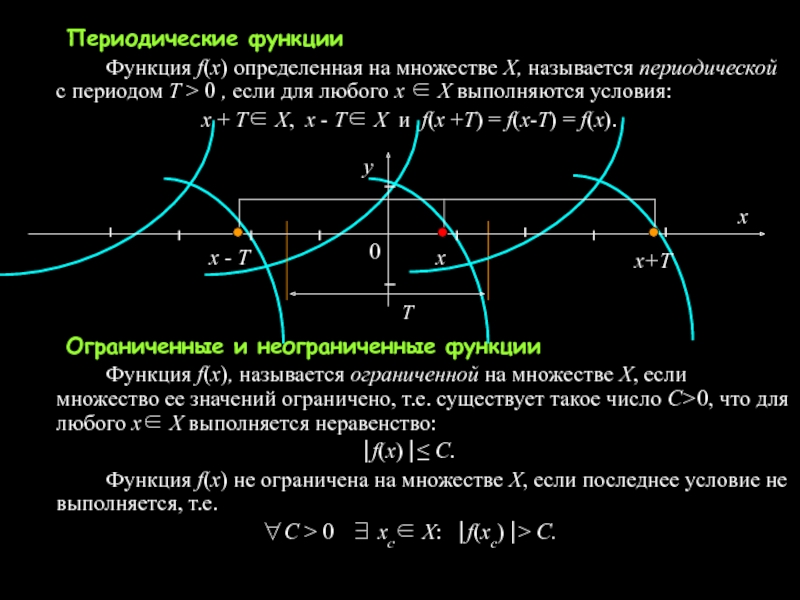
Слайд 26 Периодические функции
Функция f(x) определенная на множестве X, называется периодической
с периодом Т > 0 , если для любого x
∈ X выполняются условия:x + T∈ X, x - T∈ X и f(x +T) = f(x-T) = f(x).
Ограниченные и неограниченные функции
Функция f(x), называется ограниченной на множестве X, если множество ее значений ограничено, т.е. существует такое число C>0, что для любого x∈ X выполняется неравенство:
⎢f(x) ⎢≤ C.
Функция f(x) не ограничена на множестве X, если последнее условие не выполняется, т.е.
∀С > 0 ∃ xc∈ X: ⎢f(xc) ⎢> C.
Т
х
х+Т
х - Т
Слайд 27Монотонные функции
Функция f(x) называется возрастающей (строго возрастающей) на множестве X,
если для всех х1, х2 ∈ X, таких что х1
< х2, выполняется неравенство:f(x1) ≤ f(x2) ( f(x1) < f(x2) ).
Функция f(x) называется убывающей (строго убывающей) на множестве X, если для всех х1, х2 ∈ X, таких что х1 < х2 , выполняется неравенство:
f(x1) ≥ f(x2) (f(x1) > f(x2) ).
Возрастающие и убывающие функции называются монотонными.
х1
х1
х2
х2
f(х2)
f(х2)
f(х1)
f(х1)
Слайд 28Обратная функция
D(f) = [a, b] – область определения функции f(x),
Е(f) = [c, d] – область значений функции f(x).
Если
f(x) такова, что для любого уо∈ Е(f), уравнение f(x) = уо
имеет единственное решение, то эту функцию называют обратимой.
В этом случае, выразив х из формулы у = f(x) и поменяв затем х и у
местами, получим обратную функцию, обозначаемую символом f -1или g:
у = f -1(x) = g(x), x∈ D(g).
y0
x1
x2
a
b
c
d
y = f(x)
x
y
0
y
x
a
b
c
d
y = f(x)
y0
x0
0
Слайд 29 Отметим следующие свойства, показывающие, как связаны данная функция и обратная
к ней:
1. Если g – функция, обратная к f,
то f – функция, обратная к g; при этом D(g) = Е(f), Е (g) = D (f).
2. g(f(x)) = x ,∀x∈ D (f); f (g (x)) = x, ∀x∈ E(f).
3. Если f – строго монотонная функция, то она обратима.
4. График обратной функции у = g(x), симметричен графику функции
y = f(x) относительно прямой у = х.
y = f(x)
y = g(x)
y
x
y0
y0
x0
x0
y = x
(x0, y0)
(y0, x0)
0















![Математический анализ .Отрезок [a, b] = {x: a ≤ x ≤ b} Интервал .Отрезок [a, b] = {x: a ≤ x ≤ b} Интервал (a, b) = {x: a <](/img/thumbs/d7eb63959c814804c4925e5a051970d5-800x.jpg)








![Математический анализ Обратная функция D(f) = [a, b] – область определения функции f(x), Е(f) Обратная функция D(f) = [a, b] – область определения функции f(x), Е(f) = [c, d] – область значений](/img/thumbs/d02cce8149b2e2862f82e934e0759ddc-800x.jpg)





















