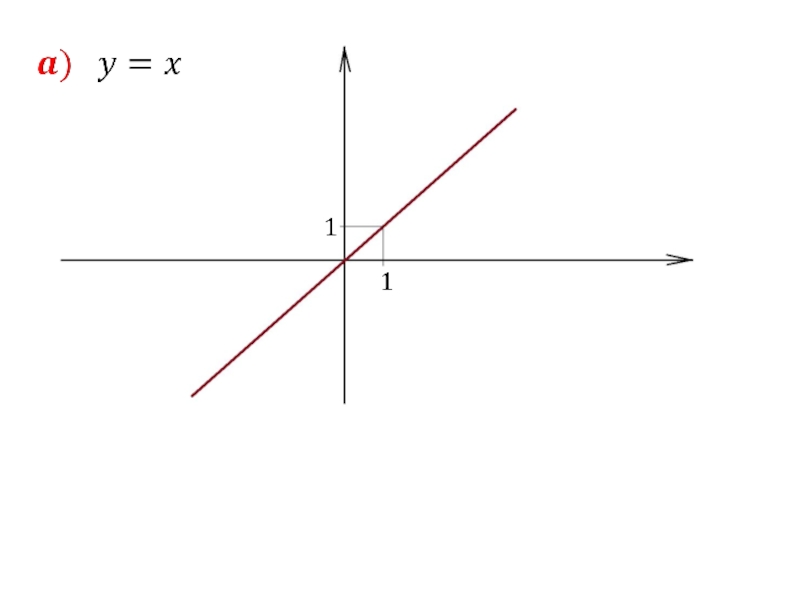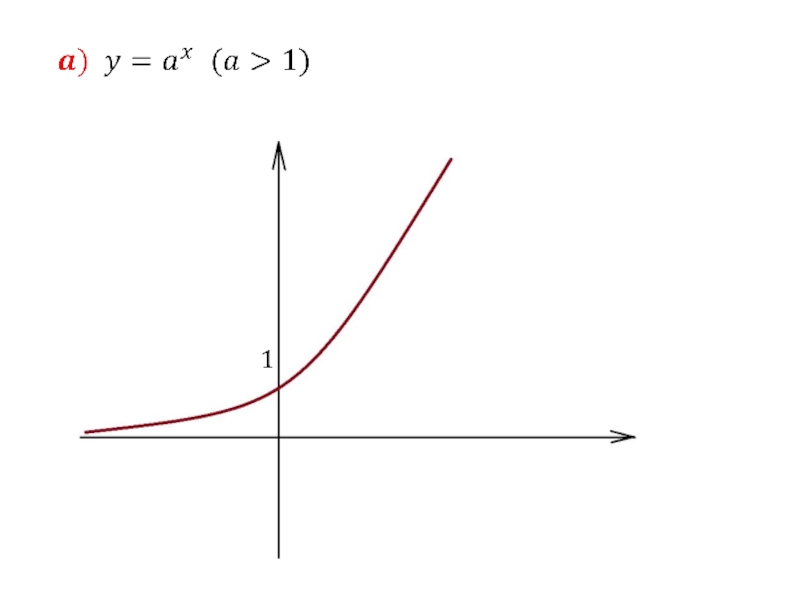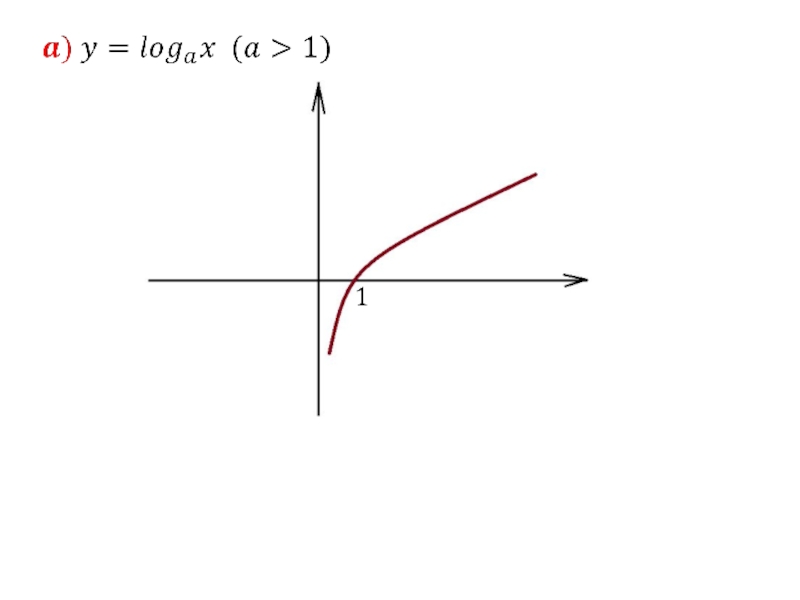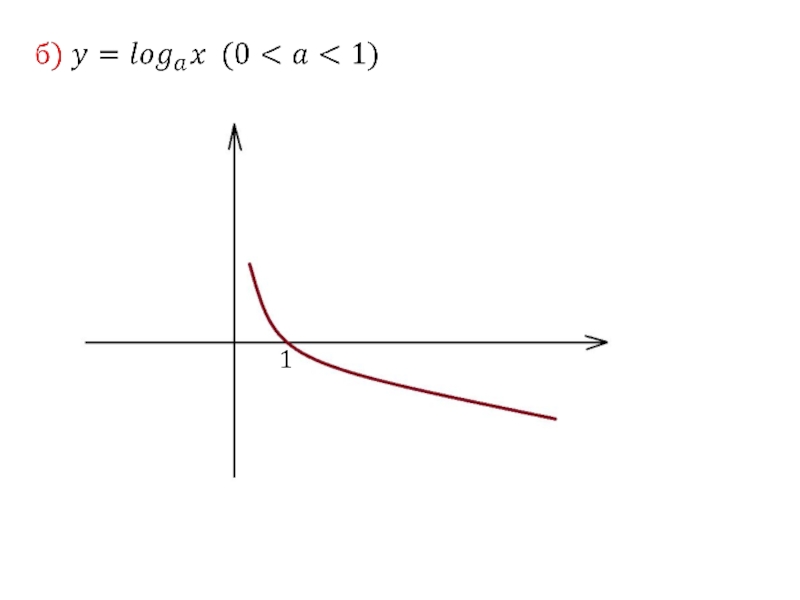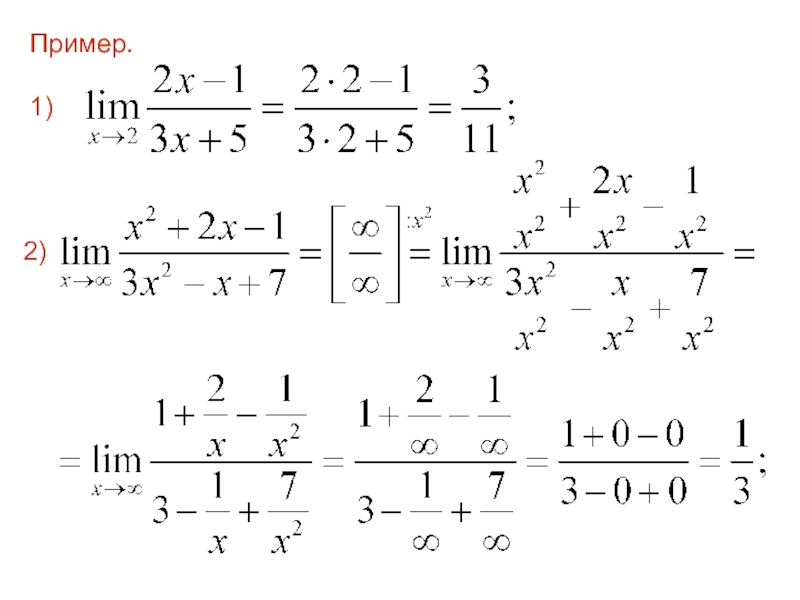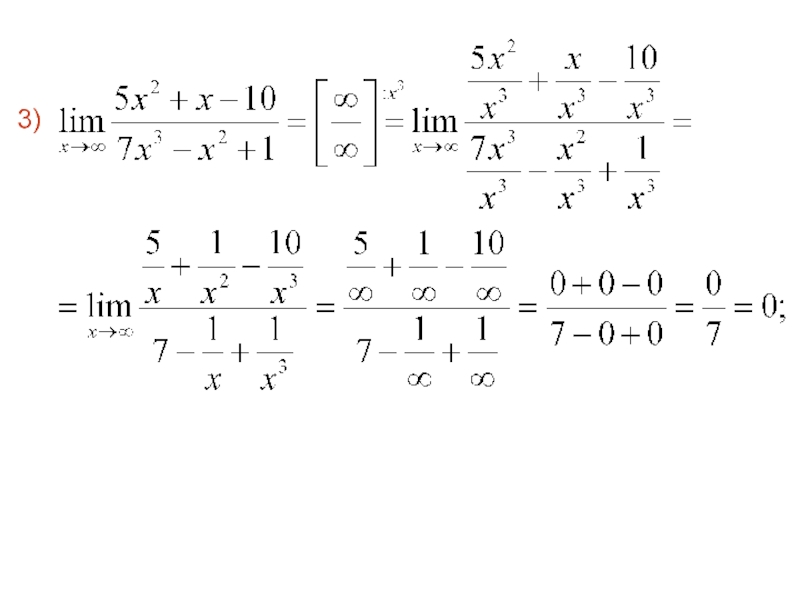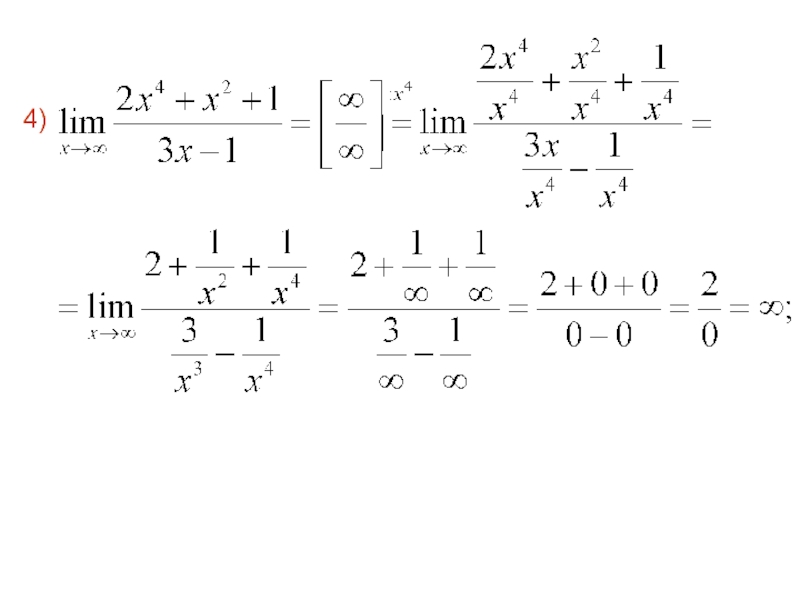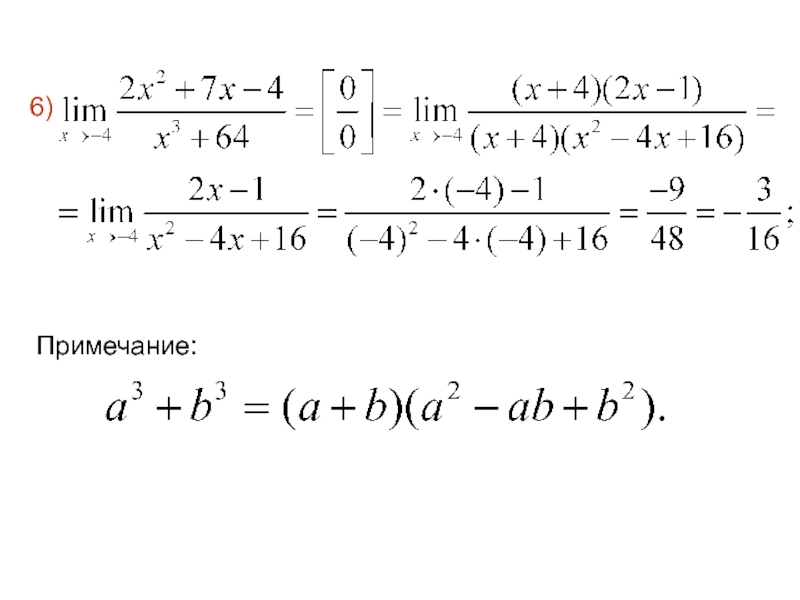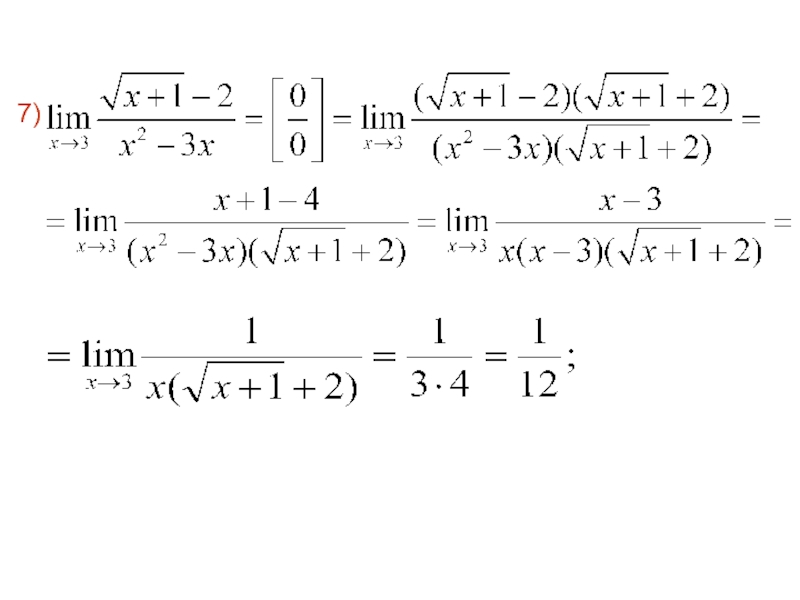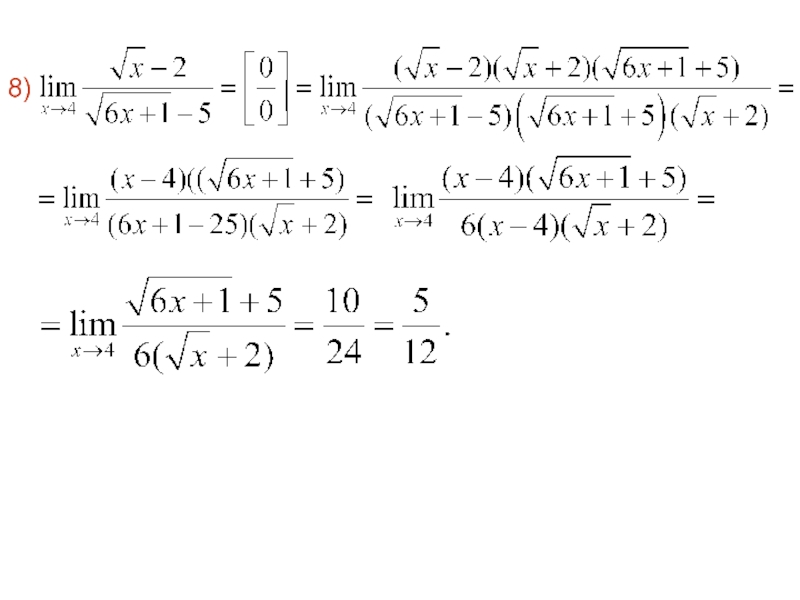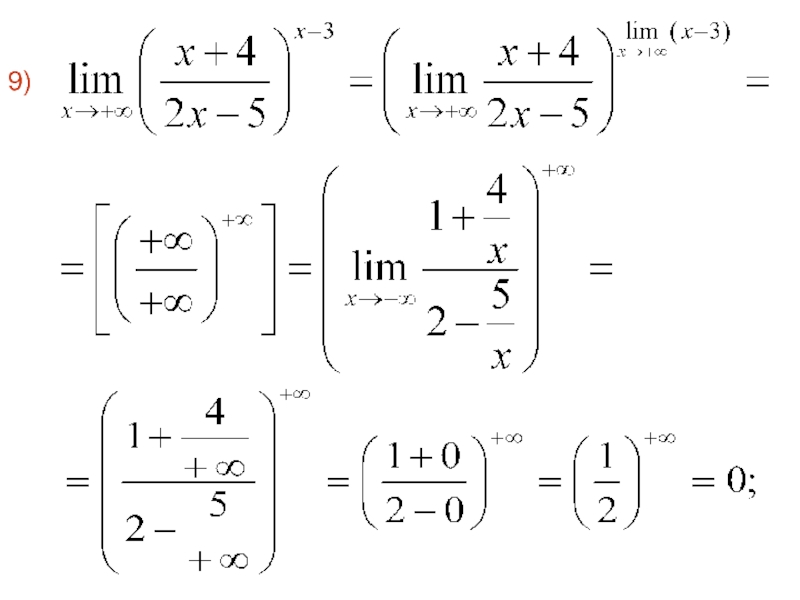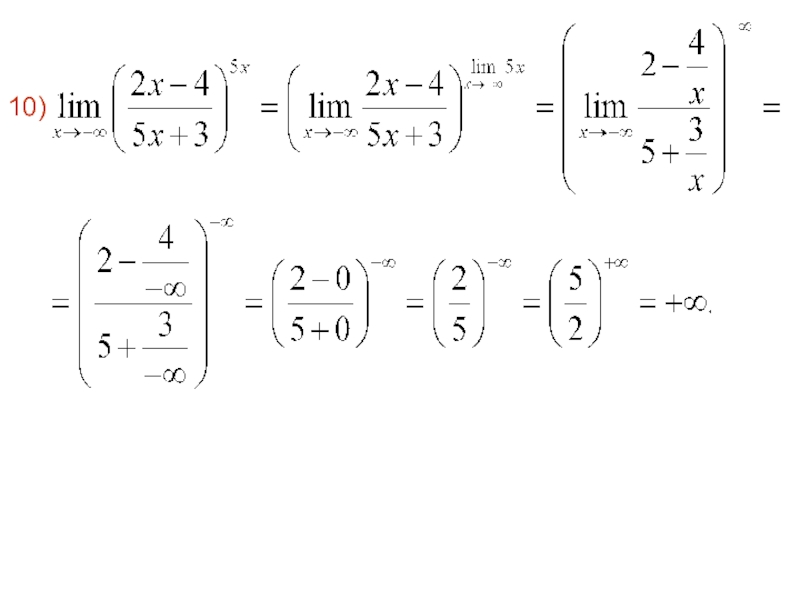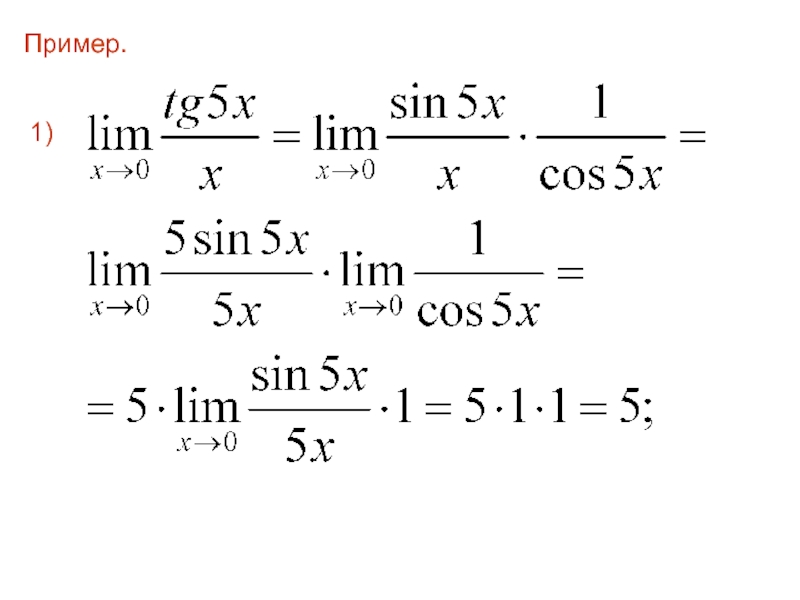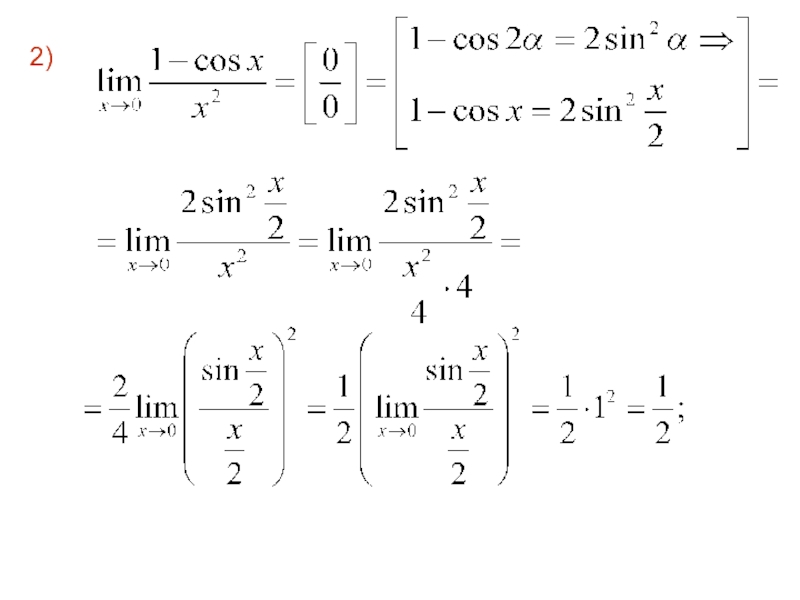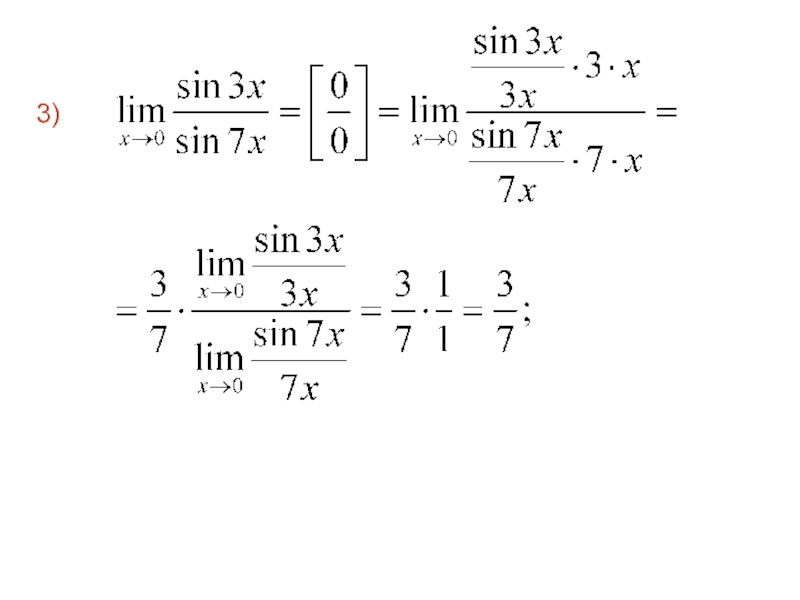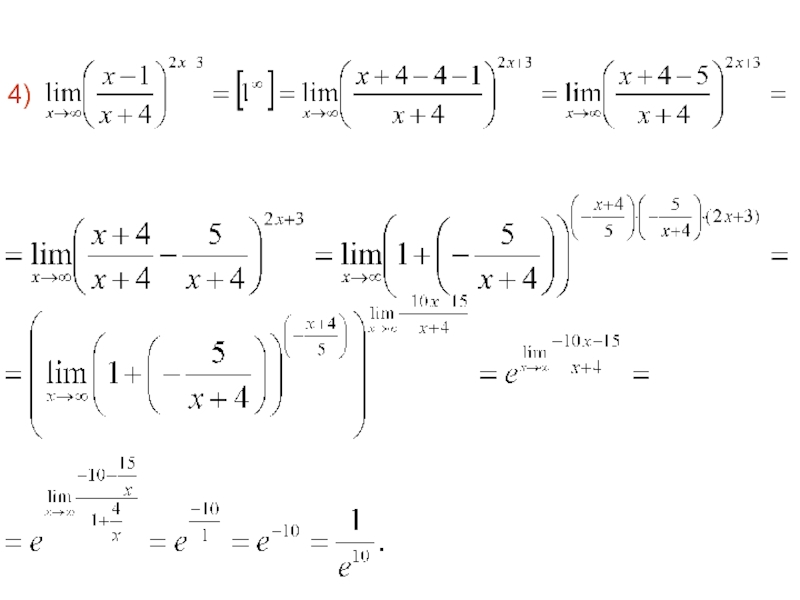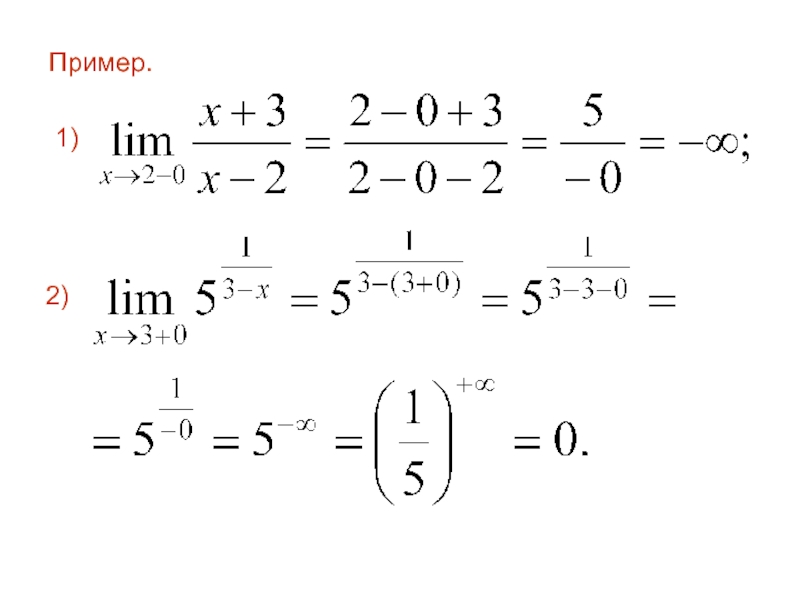Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Содержание
- 1. МАТЕМАТИЧЕСКИЙ АНАЛИЗ
- 2. Глава 1. Введение в математический анализ. Множества,
- 3. Множества, элементами которых являются числа, называют числовыми.
- 4. Бер Л.М. Введение в анализ.
- 5. Бер Л.М. Введение в анализ.
- 6. Бер Л.М. Введение в анализ.
- 7. Бер Л.М. Введение в анализ.
- 8. Бер Л.М. Введение в анализ.
- 9. Бер Л.М. Введение в анализ.
- 10. В дальнейшем для сокращения записей будем использовать
- 11. §2 Числовые промежутки. Окрестность точки. Пусть и
- 12. Числа и называются соответственно левым
- 13. Слайд 13
- 14. §3 Понятие функции. Способы задания функций. Пусть
- 15. Пусть функция такова, что для В
- 16. Если где R, то функция называется
- 17. 1) графический: задается график функции; 2) табличный:
- 18. §4 Основные характеристики функции. 1) Функция определенная
- 19. График четной функции симметричен относительно оси а
- 20. Интервалы, на которых функции монотонны, называются интервалами
- 21. §5 Основные элементарные функции и их графики.
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
- 26. Слайд 26
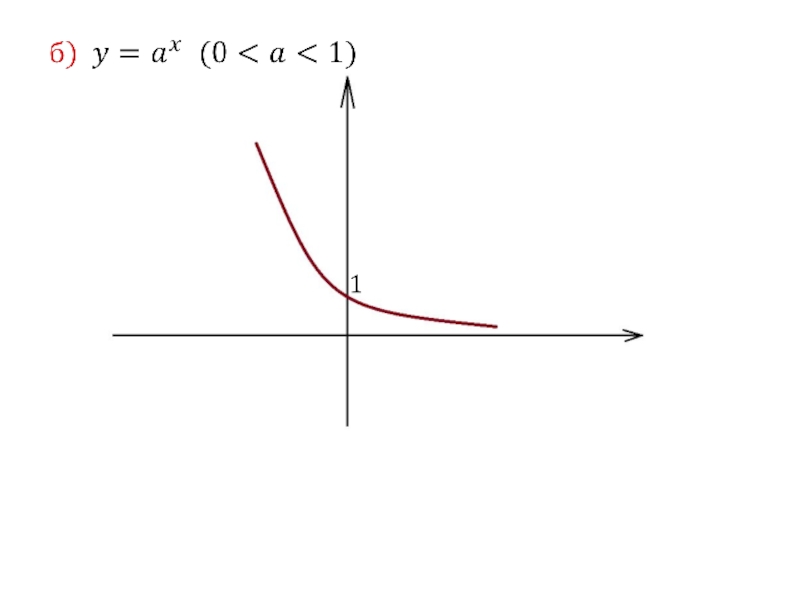
- 27. 2. Показательная функция
- 28. Слайд 28
- 29. Слайд 29
- 30. 3. Логарифмическая функция
- 31. Слайд 31
- 32. Слайд 32
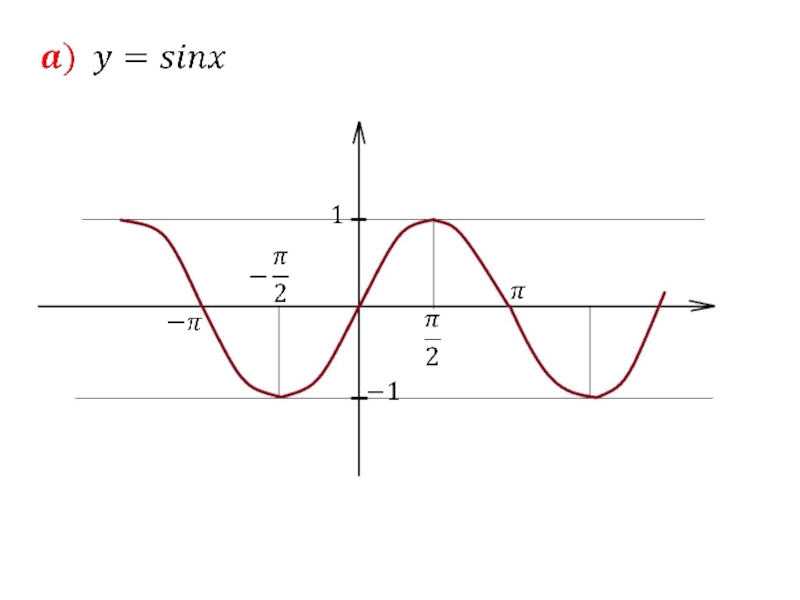
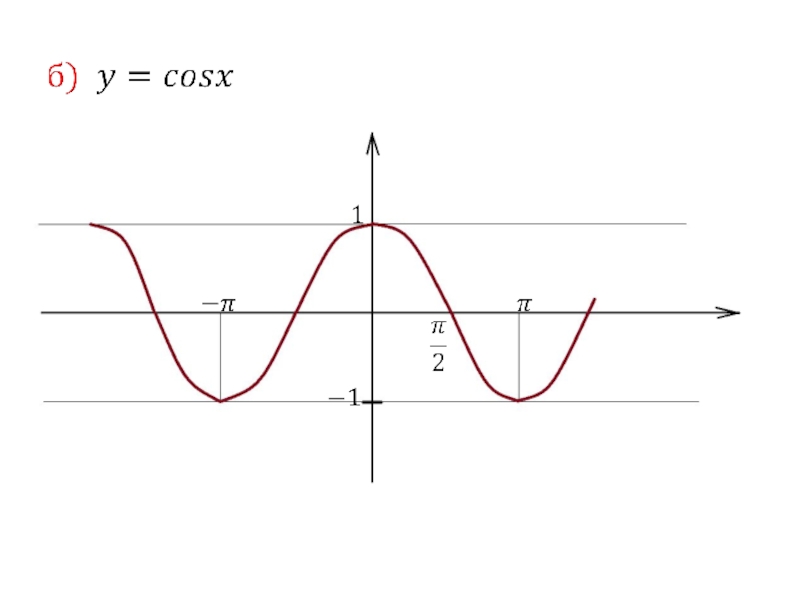
- 33. 4. Тригонометрические функции
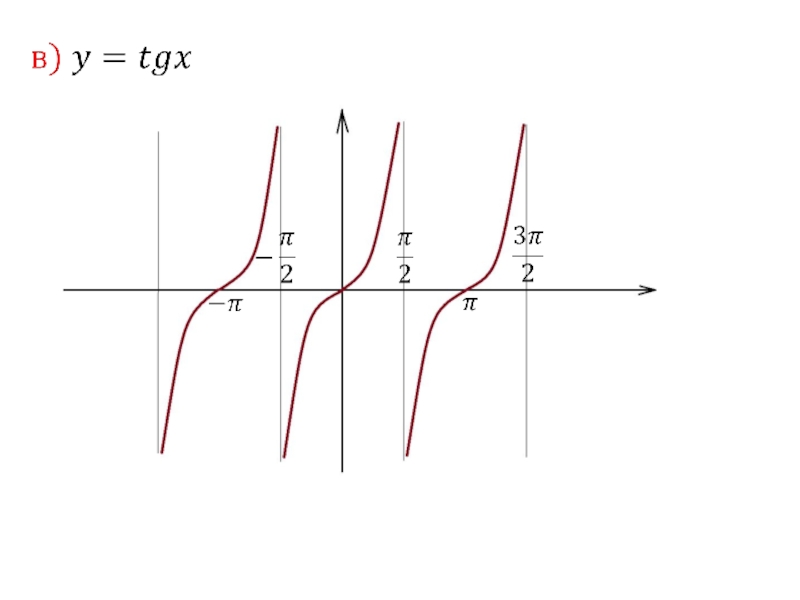
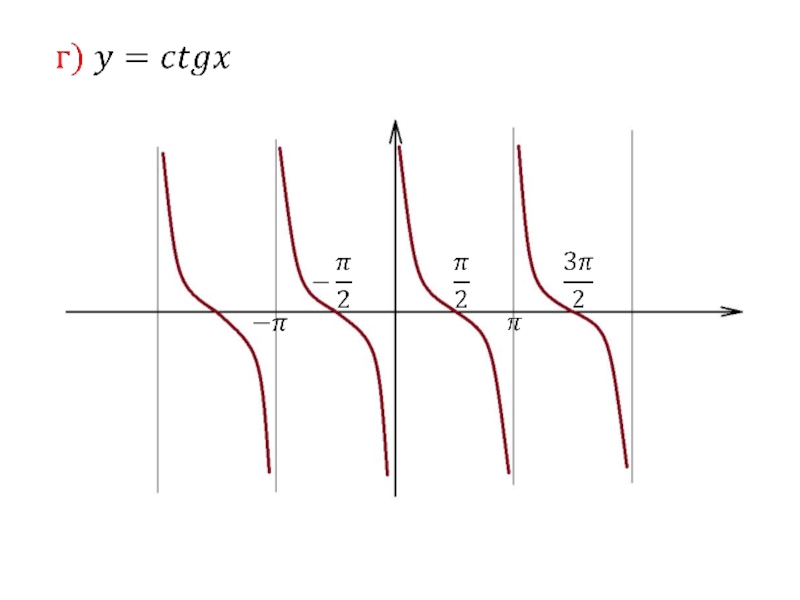
- 34. Слайд 34
- 35. Слайд 35
- 36. Слайд 36
- 37. Слайд 37
- 38. 5. Обратные тригонометрические функции.
- 39. Функция, задаваемая одной формулой и постоянных с
- 40. Примеры неэлементарных функций: где
- 41. Глава 2. Теория пределов.§1 Числовая последовательность. Предел
- 42. Пример. Формула задает последовательность:
- 43. Пусть функция последовательнопринимает значения т.е.пробегает последовательность Важным
- 44. Для точного определения понятия «предел» введем произвольное
- 45. Пусть этому моменту отвечает значение оно, очевидно,
- 46. Число называется пределомесли для любогонайдется такое натуральноечто
- 47. Кратко определение предела можно записать так: (6.1)
- 48. Поэтому определение предела последовательности можносформулировать так: число
- 49. Ясно, что чем меньше тем больше число
- 50. Преобразуем последнее неравенство Таким образом, можно взять
- 51. Итак, для указано соответствующее значение Это и
- 52. §2 Предел функции в точке. Бесконечно большая
- 53. Слайд 53
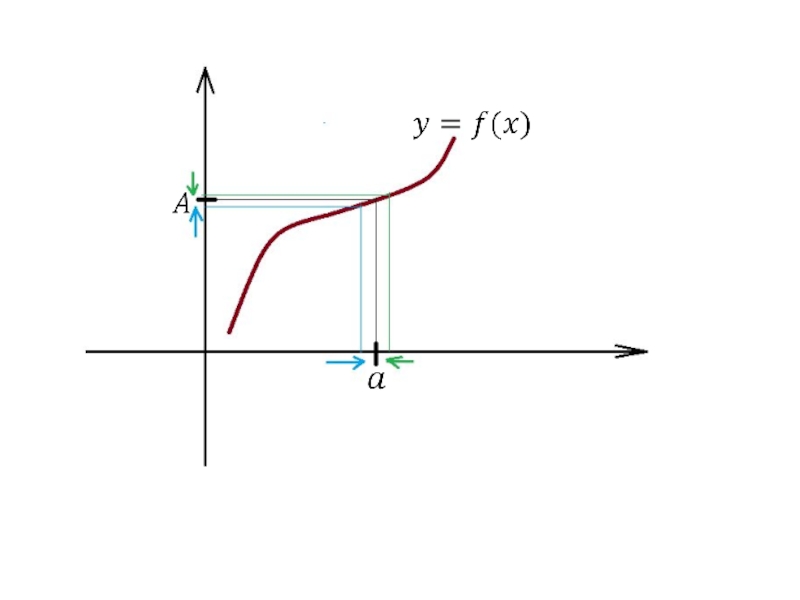
- 54. Определение. Число называется пределом функции при если
- 55. Слайд 55
- 56. Бесконечно большая функция (б.б.ф). Определение. Функция называется
- 57. Бесконечно малая функция (б.м.ф.).
- 58. Теорема. 1) Если б.м.ф. в то
- 59. Символически это утверждение можно записать так: и
- 60. §3 Вычисление пределов. Практическое вычисление пределов основывается
- 61. 4) 5) 6) 7)
- 62. При применении этой теоремы необходимо иметь в
- 63. А если условия этой теоремы не выполнены,
- 64. Кроме того, будем пользоваться тем фактом, что
- 65. Также при нахождении пределов полезно иметь в виду следующие свойства показательной функции:
- 66. Пример. 1) 2)
- 67. 3)
- 68. 4)
- 69. 5) Примечание: где и корни соответствующего квадратногоуравнения.
- 70. 6) Примечание:
- 71. 7)
- 72. 8)
- 73. 9)
- 74. 10)
- 75. §4 Первый и второй замечательные пределы. Замечательными
- 76. Второй: или или или где экспонента,
- 77. Первый замечательный предел применяется для раскрытиянеопределенности вида
- 78. Пример. 1)
- 79. 2)
- 80. 3)
- 81. 4)
- 82. §5 Односторонние пределы. В определении предела считается,
- 83. Слайд 83
- 84. Определение. Число называется пределом функции слева в точке если и обозначается или
- 85. Определение. Число называется пределом функции справа в точке если и обозначается или
- 86. Пределы слева и справа называются односторонними пределами.
- 87. Пример. 1) 2)
- 88. §6 Непрерывность функции. Классификация точек разрыва. Пусть
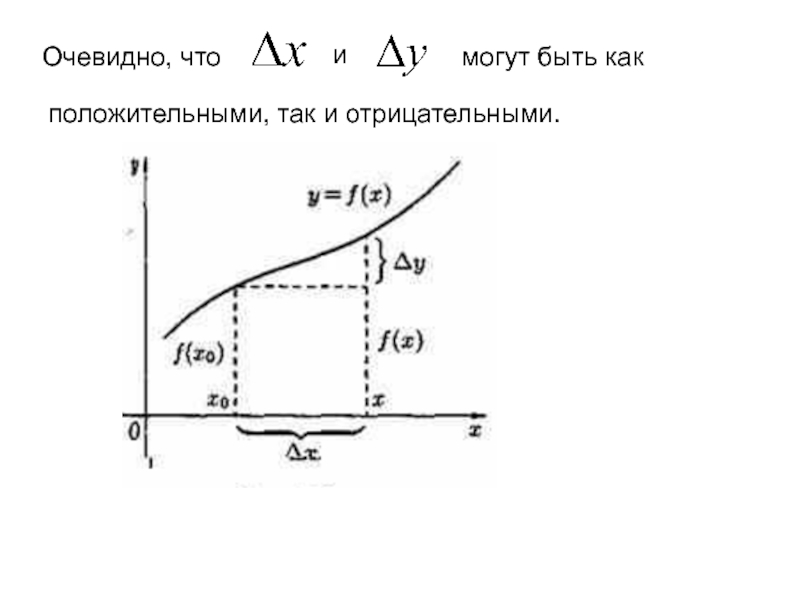
- 89. Очевидно, что и могут быть какположительными, так и отрицательными.
- 90. Определение 1. Функция называется непрерывной в точке
- 91. Определение 2. Функция называется непрерывной в точке
- 92. Если функция непрерывна в каждой точкенекоторого множества,
- 93. а при нарушении условия 4) называется точкойустранимого
- 94. 4) Если функция непрерывна на отрезке, то
- 95. Решение. а) Функция является элементарной, а следовательно,
- 96. Поскольку один из односторонних пределов равенбесконечности, т.е.
- 97. Так как и то в точке исходная
- 98. Глава 3. Дифференциальное исчисление
- 99. ОПРЕДЕЛЕНИЕ. Производной функции y = f(x) в точке x0
- 100. ТЕОРЕМА 1 (необходимое и достаточное условие существо-
- 101. Соответствие x0 f (x0) является функцией, определенной на множестве
- 102. 2. Физический и геометрический смысл производной 1)
- 103. 2) Геометрический смысл производной.Пусть ℓ – некоторая
- 104. Рассмотрим кривую y = f(x). Пусть в точке M0(x0 ; f(x0))
- 105. Замечания. 1) Прямая, проходящая через точку M0 перпендикулярно
- 106. 3. Правила дифференцирования 1) Производная константы равна нулю,
- 107. Слайд 107
- 108. По определению и с помощью правил дифференцирования
- 109. §2. Дифференциал функции 1. Определение и геометрический
- 110. ТЕОРЕМА 1 (о связи дифференцируемости с существованием
- 111. Замечание. Из теоремы 1 следует, что нахождение
- 112. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ДИФФЕРЕНЦИАЛАРассмотрим график функции y = f(x). Пусть
- 113. Замечания. 1) Так как для дифференциала функции
- 114. 2. Свойства дифференциалов Из теоремы 1 и
- 115. 6) Формула dy = f (x) dx справедлива не только в
- 116. §3. Производные и дифференциалы высших порядков 1.
- 117. Если f (x) тоже дифференцируема на некотором множестве
- 118. ФИЗИЧЕСКИЙ СМЫСЛ второй производной. Если S = S(t) – расстояние,
- 119. 2. Дифференциалы высших порядков Пусть y = f(x) дифференцируема
- 120. Продолжая далее этот процесс, определим дифференциал n-го
- 121. Замечания.1) Скобки в правой части формулы (2) обычно
- 122. §4. Использование производной при вычислении пределов
- 123. Замечания.1) Если f (x) и (x) тоже являются
- 124. §5. Исследование функций и построение графиков1. Возрастание
- 125. Интервалы возрастания и убывания функции называются интервалами
- 126. 2. Экстремумы функцииПусть x0D(f ), x0 –
- 127. Замечания:1) Понятия минимум и максимум функции близки
- 128. 2) Функция может иметь в своей области определения
- 129. ТЕОРЕМА 2 (необходимое условие экстремума, теорема Ферма).
- 130. ТЕОРЕМА 3 (достаточное условие экстремума). Пусть x0
- 131. 3. Выпуклость и вогнутость кривой. Точки
- 132. Точки кривой, которые разделяют ее выпуклые и
- 133. ОПРЕДЕЛЕНИЕ. Кривая y = f(x) называется выпуклой (вогнутой) на
- 134. ТЕОРЕМА 5 (необходимое и достаточное условия выпуклости
- 135. СЛЕДСТВИЕ 6 (необходимое условие перегиба кривой y = f(x)).
- 136. 4. Асимптоты кривой ОПРЕДЕЛЕНИЕ. Прямая ℓ называется
- 137. ТЕОРЕМА 8 (необходимое и достаточное условие существова-
- 138. ТЕОРЕМА 9 (необходимое и достаточное условие существова-
- 139. СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ Найти область определения функции.Исследовать
- 140. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Глава 1. Введение в математический анализ.
Множества, функции.
§1 Множества. Основные
определения.
признаку. Объекты, из которых состоит множество, называют его элементами. Множество, не содержащее ни одного элемента, называют пустым и обозначают .Слайд 3Множества, элементами которых являются числа, называют числовыми. Примерами числовых множеств
являются:
N
множество натуральных чисел;
Z
множество
целых чисел; Q
множество рациональных
чисел;
R
множество действительных чисел.
Слайд 4Бер Л.М. Введение в анализ.
ТПУ Рег. № 282 от 25.11.2009
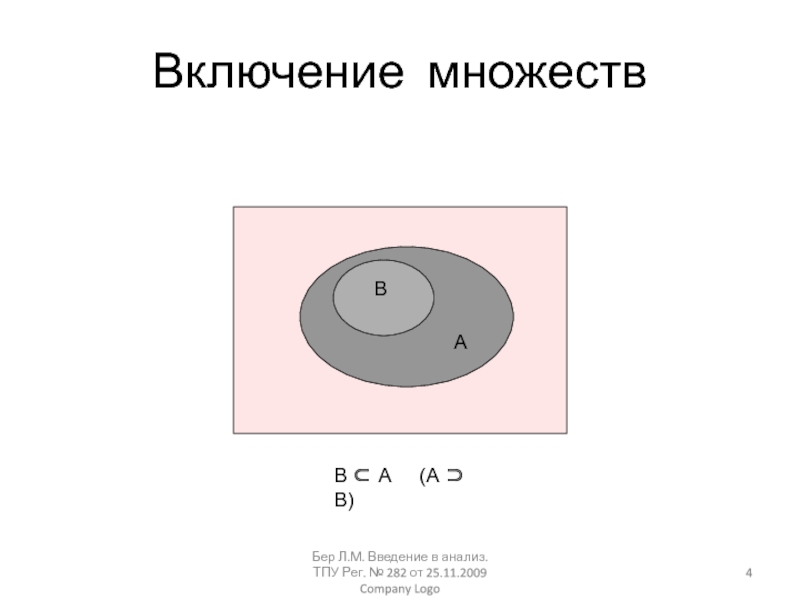
Company LogoВключение множеств
В
А
В А (А В)
Слайд 5Бер Л.М. Введение в анализ.
ТПУ Рег. № 282 от 25.11.2009
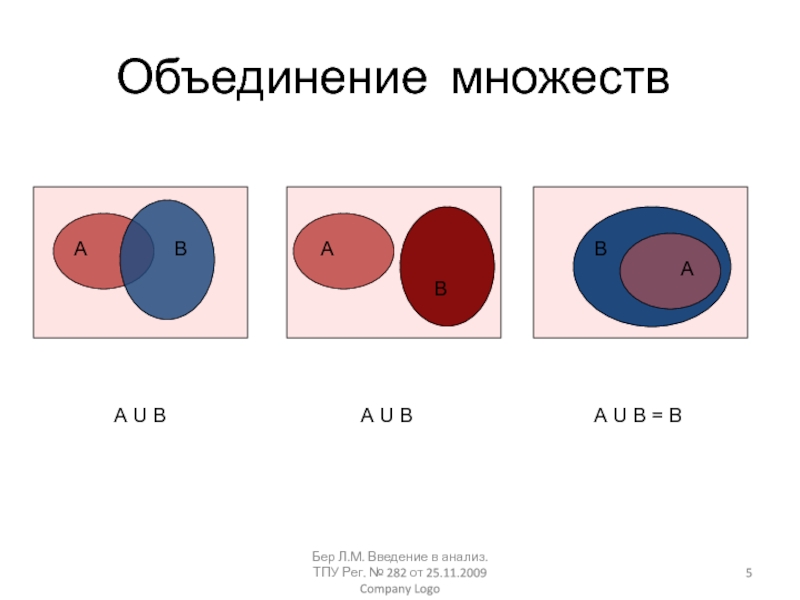
Company LogoОбъединение множеств
А U В
А U В
А U В = В
А
А
А
В
В
В
Слайд 6Бер Л.М. Введение в анализ.
ТПУ Рег. № 282 от 25.11.2009
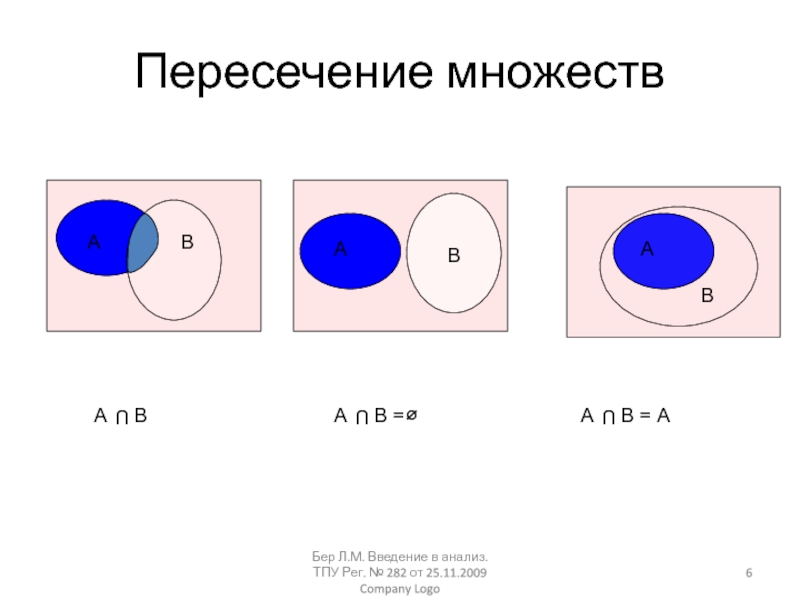
Company LogoПересечение множеств
А
А
А
А
А
А
U
U
U
В
В
В
В
В =
В = A
Слайд 7Бер Л.М. Введение в анализ.
ТПУ Рег. № 282 от 25.11.2009
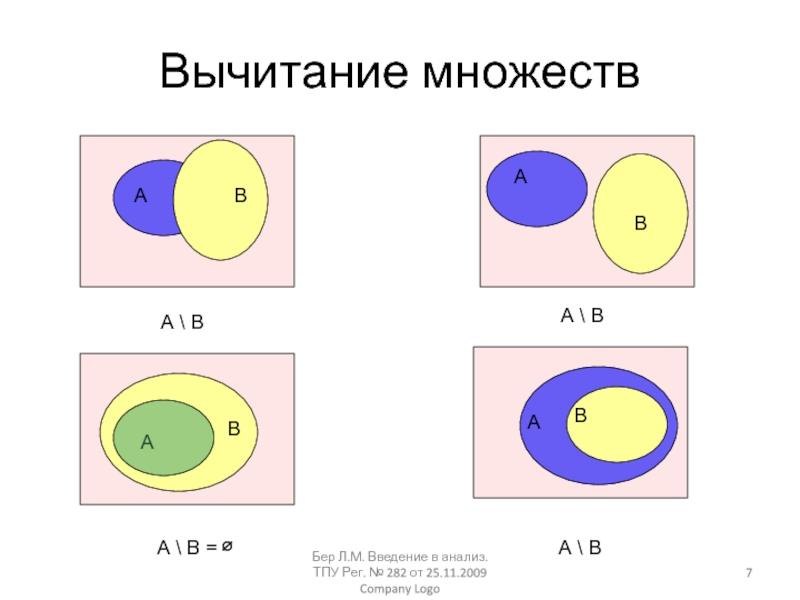
Company LogoВычитание множеств
А \ В
А \ В =
А \ В
А \ В
А
А
А
А
В
В
В
В
Слайд 8Бер Л.М. Введение в анализ.
ТПУ Рег. № 282 от 25.11.2009
Company LogoЧисловые множества
1. N, Z, Q, I, R, RR, C.
2. Подмножества вещественных чисел:
Пусть .
Отрезок, сегмент: ;
Интервал: ;
Полуинтервал: , ;
Замкнутый луч: , ;
Открытый луч: , .
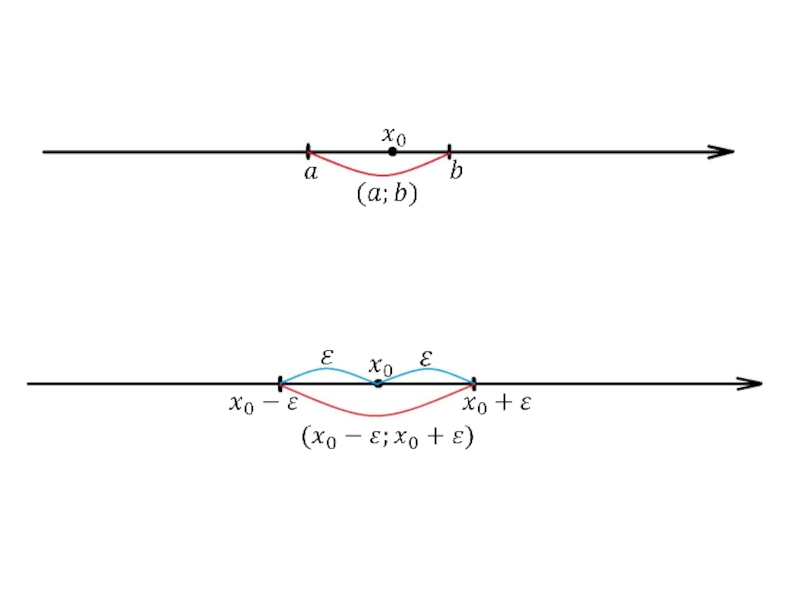
Определение. Пусть x0 R, > 0. Интервал (x0-, x0+) будем называть -окрестностью точки x0 .
Обозначение: U(x0,)= (x0-, x0+)= {x R | |x - x0|<}.
Слайд 9Бер Л.М. Введение в анализ.
ТПУ Рег. № 282 от 25.11.2009
Company LogoЧисловые множества
R +, – =
Пусть > 0. Тогда
U(+,)=(1/; +)+=x | x > 1/ ;
U(–,)=(–; –1/)–=x | x < – 1/ ;
U(,)=(–; –1/)(1/; +)=x | |x|> 1/ .
Слайд 10В дальнейшем для сокращения записей будем использовать некоторые логические символы:
означает «для любого», «для всякого», «каждый»;
означает «существует», «найдется»; : «имеет место», «такое, что»;
«предложения
и
равносильны»;
«из предложения
следует
предложение
» .
Слайд 11§2 Числовые промежутки. Окрестность точки.
Пусть
и
действительные
числа, причем
Числовыми промежутками (интервалами) называются подмножества всех действительных чисел,
имеющих следующий вид
отрезок;
интервал;
полуинтервал;
полуинтервал.
Слайд 12Числа
и
называются соответственно левым и
правым концами
промежутков.
Пусть
любое действительное число (точка на
числовой оси).
Окрестностью точки
называется
любой интервал
содержащий точку
В частности, интервал
, где
называется
-окрестностью точки
Слайд 14§3 Понятие функции. Способы задания функций.
Пусть даны два непустых
множества
и
Правило
по которому каждому элементу
поставлен в соответствие один и только один элемент
называется функцией и записывается
или
При этом множество
называется областью
определения функции
и обозначается
или
а множество
множеством значений
функции
и обозначается
или
Слайд 15Пусть функция
такова, что для
В этом случае любому
элементу
может быть
поставлен в соответствие единственный элемент
тем самым определена новая
функция
называемая обратной
заданной функции
Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов.
Слайд 16Если
где
R, то функция
называется сложной функцией или
композицией
функций
и
Чтобы задать функцию
необходимо указать
правило, позволяющее, зная
находить
соответствующее
значение Существуют три способа задания функций:
Слайд 171) графический: задается график функции;
2) табличный: функция задается таблицей
ряда значений аргумента и соответствующих значений функции;
3) аналитический: функция
задается в виде одной или нескольких формул или уравнений. Аналитический способ задания функции является наиболее совершенным, так как к нему приложены методы математического анализа, позволяющие полностью исследовать функцию
Слайд 18§4 Основные характеристики функции.
1) Функция
определенная на множестве
называется
четной, если
выполняются условия:
и
нечетной, если
выполняются условия:
и
Из определения следует, что если функция задана
аналитически и ее область определения
не является
симметричным относительно точки
множеством,
то функция не может быть ни четной, ни нечетной.
Слайд 19График четной функции симметричен относительно оси
а нечетной относительно
начала координат.
2) Функция
называется возрастающей на
на интервале
если
выполняется
условие Функция
называется убывающей на
на интервале
если
выполняется условие
Возрастающие и убывающие функции называются строго монотонными.
Слайд 20Интервалы, на которых функции монотонны, называются интервалами монотонности.
3) Функцию
определенную на множестве
называют ограниченной на этом множестве,
если существует
такое число Слайд 21§5 Основные элементарные функции и их графики. Понятие элементарной функции.
Основными элементарными функциями называются следующие функции:
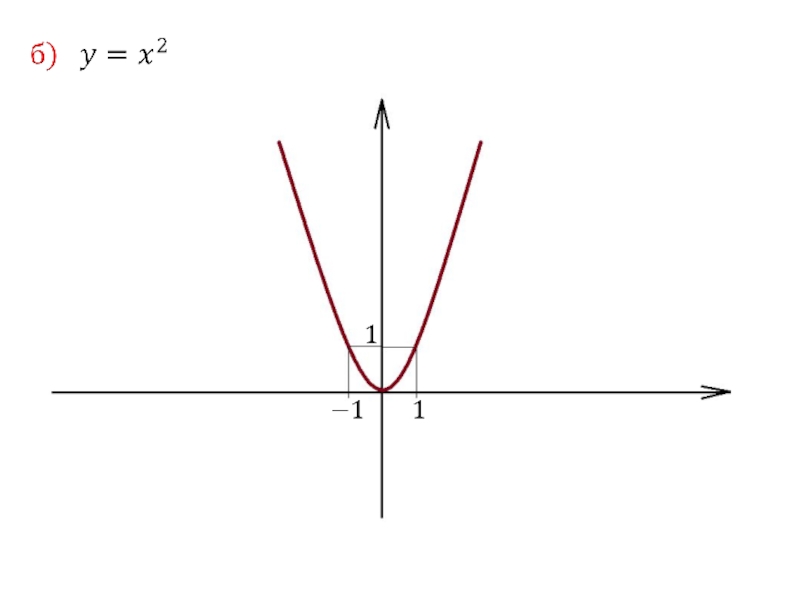
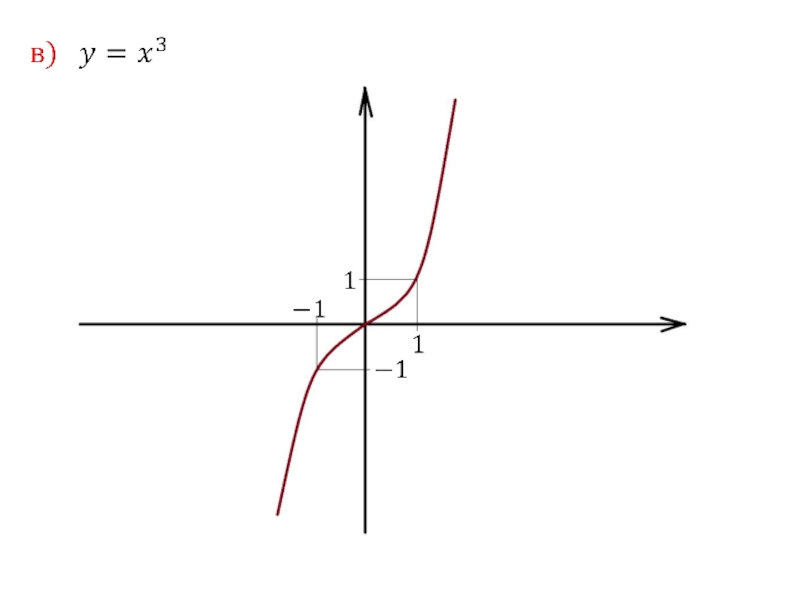
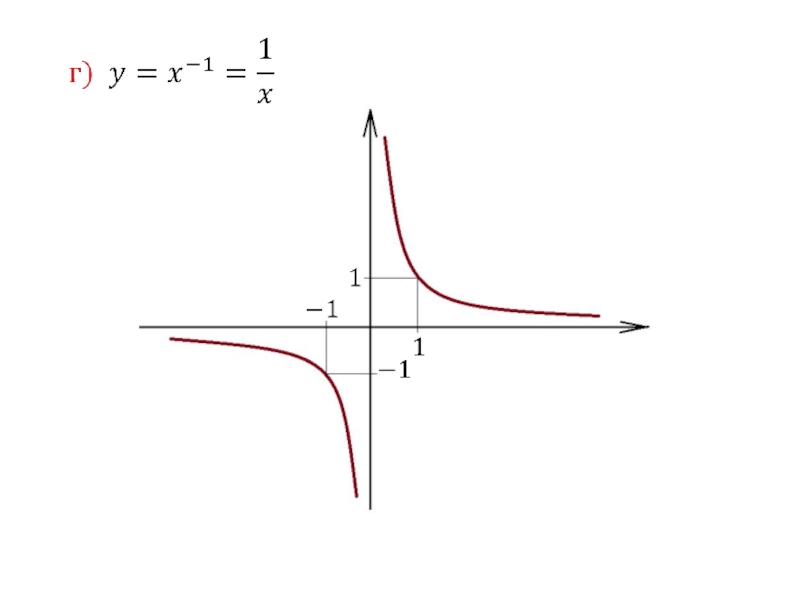
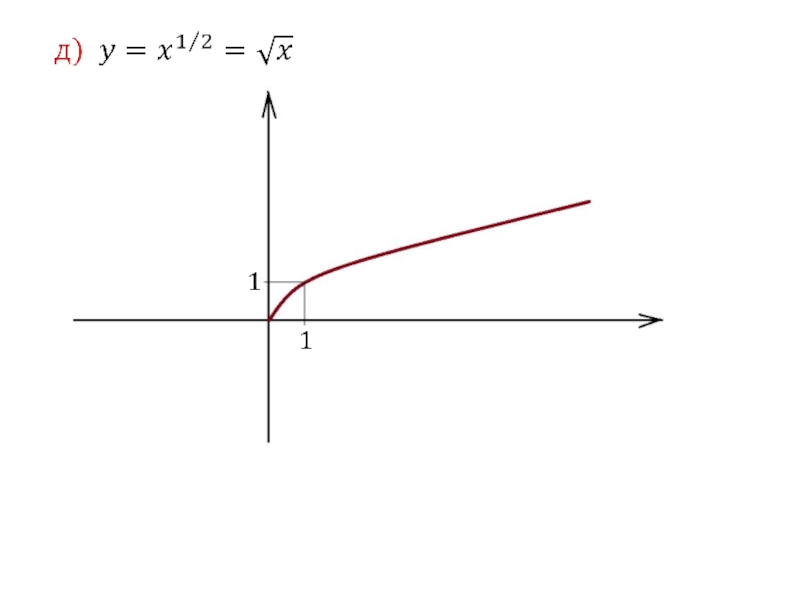
1. Степенная функция
R.
Слайд 39Функция, задаваемая одной формулой и постоянных с помощью конечного числа
арифметических операций (сложения, вычитания, умножения, деления) и композиций, называется элементарной
функцией.Примеры элементарных функций:
Слайд 41Глава 2. Теория пределов.
§1 Числовая последовательность. Предел числовой последовательности.
Функция,
областью определения которой является
множество
N натуральных чисел, называется числовой
последовательностью и
обозначается или
или
При этом
называется n-ым членом
последовательности.
Геометрически каждому члену последовательности соответствует точка на числовой оси
Слайд 43Пусть функция
последовательно
принимает значения
т.е.пробегает последовательность
Важным случаем такого изменения
функции является тот, при котором по мере возрастания номера
соответствующие
значения неограниченно
приближаются (стремятся) к некоторому постоянному
значению
в этом случае говорят, что
последовательность
стремится к пределу
Но выражения «неограниченно приближаются», «стремятся» неопределенные и поэтому не годятся для точного математического понятия предела.
Слайд 44Для точного определения понятия «предел» введем произвольное малое положительное число
оно произвольно, его по желанию можно задавать равным 0,01, и
0,001, и вообще поскольку
Факт неограниченного сближения последовательности
с постоянной
можно охарактеризовать так:
каково бы ни было малое положительное число
в процессе изменения последовательности рано или поздно должен наступить такой момент, начиная с которого все ее дальнейшие значения
будут отличаться от
по абсолютному значению меньше, чем на это произвольное
Слайд 45Пусть этому моменту отвечает значение
оно, очевидно, зависит от задания
числа
чем
меньше, тем больше должно быть
зависимость
от
записывается
в виде Итак, факт неограниченного приближения
последовательности
к постоянной
можно математически записать следующим образом:
Слайд 46Число
называется пределом
если для любого
найдется такое натуральное
что для
всех номеров
будет
выполняться
неравенство
Определение.
последовательности
положительного числа
число
Слайд 47Кратко определение предела можно записать так:
(6.1)
Геометрический смысл определения
предела последовательности:
Неравенство
равносильно неравенствам
или
т.е.
Слайд 48Поэтому определение предела последовательности можно
сформулировать так: число
называется пределом
последовательности
если
для любой
окрестности точки
найдется такой номер
что все
члены последовательности для которых
попадут в
окрестность
точки
Слайд 49Ясно, что чем меньше
тем больше число
но в любом
случае внутри
окрестности точки
находится бесконечное число членов последовательности.
Последовательность, имеющая предел, называется
сходящейся.
В противном случае расходящейся.
Пример. Доказать, что
Решение. Воспользуемся определением (6.1):
Слайд 50Преобразуем последнее неравенство
Таким образом,
можно взять
равным
ближайшему по избытку
к
натуральному числу, т.е.
равным
где
Слайд 51Итак, для
указано соответствующее значение
Это и доказывает, что
целая часть числа
т.е. наибольшее целое
число, не превосходящее
Например, для
соответствующее значение
т.е. все члены последовательности,
начиная с
попадут в интервал
Слайд 52§2 Предел функции в точке. Бесконечно большая и бесконечно малая
функция.
Рассмотрим функцию
непрерывно изменяющегося аргумента
и предположим, что аргумент
стремится к
некоторому числу
Может случиться, что при неограниченном приближении
аргумента
к числу
соответствующие
значения функции
неограниченно
приближаются к некоторому числу
Слайд 54Определение. Число
называется пределом функции
при
если при всяком положительном
числе
можно указать другое положительное число
зависящее от выбора
такое, что
абсолютнаявеличина разности
будет меньше
когда абсолютная величина разности
будет меньше
т.е. если числовые значения функции
будут заключены в произвольной
-окрестности
числа
при условии, что числовые значения аргумента
взяты в достаточно малой
-окрестности числа
(исключая само число
):
Слайд 56Бесконечно большая функция (б.б.ф).
Определение. Функция
называется б.б.ф. при
если
для любого числа
найдется такое положительное число
зависящее от выбора
что для всех
удовлетворяющих условию
будет выполняться:
Слайд 57Бесконечно малая функция (б.м.ф.).
Связь между б.м.ф. и б.б.ф.
Определение. Функция
называется б.м.ф.
при
если для любого числа
найдется такое положительное число
зависящее от
выбора
что для всех
удовлетворяющих условию
будет выполняться:
Слайд 59Символически это утверждение можно записать так:
и
где символы
и
следует понимать как
неограниченно близкое приближение к нулю и к бесконечности
соответственно. Слайд 60§3 Вычисление пределов.
Практическое вычисление пределов основывается на связи между
б.м.ф. и б.б.ф. и на следующей теореме.
Теорема.
Если
и
то:
1)
2)
3)
Слайд 62При применении этой теоремы необходимо иметь в виду, что для
любого ненулевого числа
справедливо:
1)
2)
3)
5)
4)
6)
9)
8)
7)
10)
11)
Слайд 63А если условия этой теоремы не выполнены, то могут возникнуть
неопределенности вида
которые в простейших случаях раскрываются с помощью
алгебраических преобразований данного выражения и отыскание предела в таких случаях называют раскрытием неопределенностей. Слайд 64Кроме того, будем пользоваться тем фактом, что для всех основных
элементарных функций в любой точке их области определения имеет место
равенствоПоследнее равенство можно понимать так: вычисление любого предела нужно начинать с непосредственной подстановки предельного значения, и, если нет неопределенностей, то сразу записать ответ.
Слайд 65Также при нахождении пределов полезно иметь в виду следующие свойства
показательной функции:
Слайд 75§4 Первый и второй замечательные пределы.
Замечательными (ввиду большого числа
их применений) назвали следующие два предела
Первый:
или
Слайд 77Первый замечательный предел применяется для раскрытия
неопределенности вида
при вычислении пределов,
содержащих тригонометрические функции.
Второй замечательный предел используется для раскрытия
неопределенности вида
Слайд 82§5 Односторонние пределы.
В определении предела
считается, что
стремится к
любым способом:
оставаясь меньшим, чем
(слева от
),
большим, чем
(справа
от ) или колеблясь
около точки
Но бывают случаи, когда способ
приближения к
существенно влияет на значение
предела функции, поэтому вводят понятие односторонних
пределов.
Слайд 86Пределы слева и справа называются односторонними
пределами.
Примечание. Для
используется
особая запись:
вместо
и
пишут соответственно
и
Символы
следует понимать как
бесконечно
близкое приближение к нулю, оставаясь приэтом левее (правее) нуля.
Слайд 88§6 Непрерывность функции.
Классификация точек разрыва.
Пусть функция
определена в
Для
называют приращением аргумента
в точке
а
приращением функции
в точке Слайд 90Определение 1. Функция
называется непрерывной в точке
если
т.е. бесконечно
малому приращению аргумента соответствует бесконечно малое приращение функции.
Слайд 91Определение 2. Функция
называется непрерывной в точке
если
1)
определена
в точке
и ее окрестности;
2)
и
3)
4)
Слайд 92Если функция
непрерывна в каждой точке
некоторого множества, то она называется
непрерывной
на этом множестве.
Точка
называется точкой разрыва, если
хотя бы одно
из условий определения 2. Если нарушено
условие 2), то точка
называется точкой разрыва
второго рода; а если нарушены условия 3) или 4), то точка
называется точкой разрыва первого рода
(при нарушении условия 3)
называется точкой
скачка и скачок равен
Слайд 93а при нарушении условия 4)
называется точкой
устранимого разрыва).
Свойства непрерывных
функций.
1) Всякая элементарная функция непрерывна в каждой точке своей
области определения. 2) Сумма и произведение конечного числа непрерывных функций есть непрерывная функция.
3) Частное от деления двух непрерывных функций есть функция, непрерывная во всех точках, в которых знаменатель не равен нулю.
Слайд 944) Если функция непрерывна на отрезке, то она достигает на
этом отрезке своего наибольшего и наименьшего значения.
Пример. Найти точки
разрыва функции и установить их характер
а)
б)
Слайд 95Решение.
а) Функция
является элементарной,
а следовательно, по свойству 1,
и непрерывной на всем
множестве R, за исключением точки
Значит,
является
точкой разрыва данной функции. Выясним характер точки разрыва, для чего найдем
односторонние пределы в этой точке:
Слайд 96Поскольку один из односторонних пределов равен
бесконечности, т.е. не выполняется условие
2)
определения 2, то
точка разрыва второго рода.
б)
Данная функция непрерывна для так как на каждом из этих интервалов формулы, задающие
функцию, определяют элементарные функции. Точкой
разрыва может быть лишь точка
в которой меняется аналитическое выражение функции
Найдем односторонние пределы:
Слайд 97Так как
и
то в точке
исходная функция имеет точку
разрыва
первого рода, а именно точку скачка, скачок равен
Слайд 98Глава 3. Дифференциальное исчисление
функции одной переменной
Дифференциальное
исчисление – раздел математики, в котором изучаются производные и дифференциалы
функций и их применение к исследованию функций.§1. Производная функции
1. Определение производной функции. Необходимое условие существования производной
Пусть y = f(x) определена в точке x0 и некоторой ее окрестности.
Придадим x0 приращение x такое, что x0 + xD(f) .
Функция при этом получит приращение
f(x0) = f(x0 + x) – f(x0) .
Слайд 99ОПРЕДЕЛЕНИЕ. Производной функции y = f(x) в точке x0 называется предел отношения
приращения функции в этой точке к приращению аргумента x, при
x 0 (если этот предел существует и конечен), т.е.Обозначают:
Производной функции y = f(x) в точке x0 справа (слева) называется
(если этот предел существует и конечен).
Обозначают:
– производная y = f(x) в точке x0 справа,
– производная y = f(x) в точке x0 слева.
Слайд 100ТЕОРЕМА 1 (необходимое и достаточное условие существо-
вания производной).
Функция y = f(x)
имеет производную в точке x0 в этой точке существуют
и равны между собой производные функции справа и слева. ПричемТЕОРЕМА 2 (необходимое условие существования производ- ной функции в точке).
Если функция y = f(x) имеет производную в точке x0 , то функция f(x) в этой точке непрерывна.
Замечание. Непрерывность функции в точке x0 не является достаточным условием существования в этой точке производной функции.
Например, функция y = | x | непрерывна на всей области опре- деления, но не имеет производной в точке x0 = 0.
Слайд 101Соответствие x0 f (x0) является функцией, определенной на множестве D1 D(f).
Ее
называют производной функции y = f(x) и обозначают
Операцию нахождения для функции y = f(x)
ее производной функции называют дифференцированием функции f(x).Слайд 1022. Физический и геометрический смысл производной
1) Физический смысл производной.
Если функция y = f(x) и ее аргумент x являются физическими
величинами, то производная f (x) – скорость изменения величины y относительно величины x . ПРИМЕРЫ.
а) Пусть S = S(t) – расстояние, проходимое точкой за время t.
Тогда производная S (t0) – скорость в момент времени t0.
б) Пусть q = q(t) – количество электричества, протекающее через поперечное сечение проводника в момент времени t.
Тогда q (t0) – скорость изменения количества электричества в момент времени t0, т.е. сила тока в момент времени t0.
в) Пусть m = m(x) – масса отрезка [a ; x].
Тогда m (x) – скорость изменения массы в точке x0, т.е. линейная плотность в точке x0.
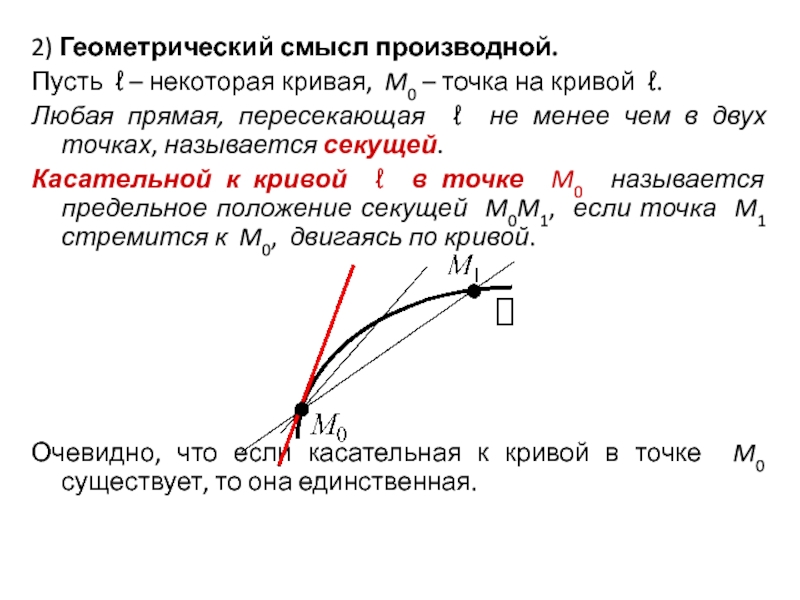
Слайд 1032) Геометрический смысл производной.
Пусть ℓ – некоторая кривая, M0 –
точка на кривой ℓ.
Любая прямая, пересекающая ℓ не менее
чем в двух точках, называется секущей. Касательной к кривой ℓ в точке M0 называется предельное положение секущей M0M1, если точка M1 стремится к M0, двигаясь по кривой.
Очевидно, что если касательная к кривой в точке M0 существует, то она единственная.
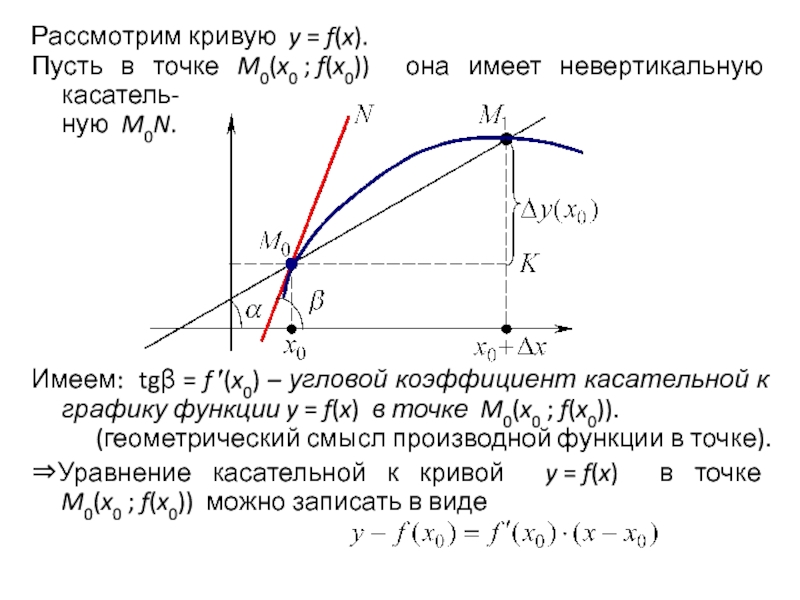
Слайд 104Рассмотрим кривую y = f(x).
Пусть в точке M0(x0 ; f(x0)) она имеет невертикальную
касатель-
ную M0N.
Имеем: tgβ = f (x0) – угловой коэффициент касательной
к графику функции y = f(x) в точке M0(x0 ; f(x0)).(геометрический смысл производной функции в точке).
Уравнение касательной к кривой y = f(x) в точке M0(x0 ; f(x0)) можно записать в виде
Слайд 105Замечания.
1) Прямая, проходящая через точку M0 перпендикулярно касательной, проведенной к
кривой в точке M0, называется нормалью к кривой в точке
M0.Т.к. для угловых коэффициентов перпендикулярных прямых справедливо равенство k1 k2 = –1 , то уравнение нормали к y = f(x) в точке M0(x0 ; f(x0)) будет иметь вид
, если f (x0) 0.
Если f (x0) = 0, то касательная к кривой y = f(x) в точке M0(x0 ; f(x0)) будет иметь вид
y = f(x0),
а нормаль x = x0.
Слайд 1063. Правила дифференцирования
1) Производная константы равна нулю, т.е.
C = 0, где
С – константа.
2) Производная суммы (разности) равна сумме (разности) производных, т.е.
3) Производная
произведения находится по правилу:Замечание. Формула дифференцирования произведения может быть легко обобщена на случай большего числа множителей. Например,
Слайд 107
, где С –
константа.Говорят: «константа выносится за знак производной».
5) Производная дроби находится по правилу:
6) Если функция (t) имеет производную в точке t, а функция f(u) имеет производную в точке u = (t), то сложная функция y = f((t)) имеет производную в точке t, причем
(правило дифференцирования сложной функции).
7) ТЕОРЕМА 3 (о производной обратной функции).
Пусть функция y = f(x) имеет производную в точке x0, причем f (x0) 0. Если существует обратная функция x = (y), то она имеет производную в точке y0 = f(x0) и
Слайд 108По определению и с помощью правил дифференцирования находят производные основных
элементарных функций (так называемая «таблица производных»).
Производная любой элементарной функции находится
с помощью таблицы производных и правил дифференцирования. Слайд 109§2. Дифференциал функции
1. Определение и геометрический смысл
ОПРЕДЕЛЕНИЕ. Функция
y = f(x) называется дифференци- руемой в точке x0 , если ее приращение
в этой точке может быть записано как сумма линейной относительно x части и бесконечно малой более высокого порядка чем x , т.е.f(x0) = A x + (x) , (1)
где A – число, (x) – б.м. более высокого порядка чем x.
Слагаемое A x в выражении (1) (т.е. линейную относи- тельно x часть f(x0)) называют дифференциалом функции y = f(x) в точке x0 и обозначают: dy(x0) , df(x0) .
Слайд 110ТЕОРЕМА 1 (о связи дифференцируемости с существованием производной).
Функция y = f(x)
дифференцируема в точке x0 она имеет в точке x0
производную. При этом для ее дифференциала в точке x0 справедливо равенствоdy(x0) = f (x0) x . (2)
Соответствие (x0 ; x) df(x0) является функцией (2-х перемен- ных).
Ее называют дифференциалом функции y = f(x) и обозначают
dy , df(x) .
Слайд 111Замечание. Из теоремы 1 следует, что нахождение производной и дифференциала
функции представляет собой по существу одну и ту же задачу.
Поэтому операцию нахождения производной называют дифференцированием функции.ОПРЕДЕЛЕНИЕ. Функция y = f(x) называется дифференци- руемой на интервале (a;b) если она дифференцируема (т.е. имеет производную) в каждой точке этого интервала.
Функция y = f(x) называется дифференцируемой на отрез- ке [a;b] если она дифференцируема на интервале (a;b) и имеет соответствующие односторонние производные в точках a и b.
Слайд 112ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ДИФФЕРЕНЦИАЛА
Рассмотрим график функции y = f(x).
Пусть функция y = f(x) дифференцируема
в точке x0.
Тогда в x0 функция f(x) имеет производную
f (x0) .в точке M0(x0 ; f(x0)) касательная к кривой y = f(x).
Дифференциал функции y = f(x) в точке x0 равен приращению ординаты точки на касательной к кривой y = f(x), которое соответствует приращению x.
Слайд 113Замечания.
1) Так как для дифференциала функции y = x справедливо
dy = dx = x ,
то говорят:
«дифференциал независимой переменной равен ее приращению».
Учитывая этот факт, формулу (2)
можно переписать в видеdy = f (x) dx . (3)
2) Из формулы (3) получаем, что производная y = f (x) явля- ется отношением 2-х дифференциалов:
Таким образом, символическая дробь превратилась в реальную дробь.
Слайд 1142. Свойства дифференциалов
Из теоремы 1 и правил дифференцирования получаем,
что справедливы следующие утверждения
1) Дифференциал константы равна нулю, т.е.
d(C) = 0 ,
где C – константа.2) Дифференциал суммы (разности) равна сумме (разности) дифференциалов, т.е. d(u v) = du dv .
3) Дифференциал произведения находится по правилу:
d(u v) = du v + u dv .
4) d(C u) = C du , где C – константа.
Говорят: «константа выносится за знак дифференциала».
5) Дифференциал дроби находится по правилу:
Слайд 1156) Формула dy = f (x) dx справедлива не только в том случае, когда
x является независимым аргументом, но и в случае, когда x
– функция.Поэтому формулу dy = f (x) dx называют инвариантной формой записи дифференциала.
Замечание. Формула
dy = f (x) x (2)
не является инвариантной. Т.е. она не будет справедлива, если x – функция.
Слайд 116§3. Производные и дифференциалы высших порядков
1. Производные высших порядков
Пусть
y = f(x) дифференцируема на множестве X1D(f) .
Тогда на X1 определена f (x).
Функцию f (x) называют также первой производной функции f(x) (или производной первого порядка функции f(x)).
Если f (x) дифференцируема на некотором множестве X2X1, то (f (x)) называют второй производной функции y = f(x) (или производной второго порядка функции f(x) ) и обозначают
Замечание. Значение второй производной функции f(x) в точке x0 обозначают
Слайд 117Если f (x) тоже дифференцируема на некотором множестве X3X2, то ее
производную (f (x)) называют третьей про- изводной функции y = f(x) (или производной
третьего порядка функции f(x)).Продолжая этот процесс, назовем n-й производной функции y = f(x) ее производную от производной порядка n – 1.
Обозначают:
– третья производная y = f(x);
– четвертая производная y = f(x);
– n-я производная y = f(x).
Производные порядка n > 1 называют производными высших порядков.
Слайд 118ФИЗИЧЕСКИЙ СМЫСЛ второй производной.
Если S = S(t) – расстояние, проходимое точкой за
время t ,
то S (t0) – скорость в момент времени
t0 , S (t0) – ускорение в момент времени t0 (скорость изменения скорости)
Справедливы следующие утверждения.
1) (C u)(n) = C u(n), где C – константа.
Говорят: «константа выносится за знак n-й производной».
2) Производная n-го порядка суммы (разности) функций равна сумме (разности) n-х производных слагаемых, т.е.
(u v)(n) = u(n) v(n) .
3) n-я производная произведения находится по формуле Лейбница :
где u(0) = u, v(0) = v.
Слайд 1192. Дифференциалы высших порядков
Пусть y = f(x) дифференцируема на множестве X1D(f) .
Дифференциал dy = f (x) dx – функция двух переменных x и dx = x.
Зафиксируем
значение dx. Тогда dy станет функцией одной переменной x.
Дифференциал функции dy(x) (если он существует) называется дифференциалом второго порядка функции y = f(x) (или вторым дифференциалом функции y = f(x)) и обозначается d 2y, d 2f(x).
d 2y – функция переменной x.
Дифференциал функции d 2y (если он существует) называют дифференциалом третьего порядка функции y = f(x) (или третьим дифференциалом функции y = f(x)) и обозначается d 3y, d 3f(x).
Слайд 120Продолжая далее этот процесс, определим дифференциал n-го порядка функции y = f(x)
как дифференциал от диффе-
ренциала порядка n – 1. Обозначают: d ny, d nf(x).
Замечание. Значение
дифференциала n-го порядка функции f(x) в точке x0 обозначают d ny(x0), d nf(x0) .Дифференциалы порядка n > 1 называют дифференциалами высших порядков.
Если функция имеет дифференциал порядка n, то ее называют n раз дифференцируемой.
ТЕОРЕМА 1 (о связи дифференциала n-го порядка и n-й производной).
Функция y = f(x) n раз дифференцируема в точке x0 она имеет в точке x0 производную порядка n. При этом для d ny(x0) справедливо равенство
d ny(x0) = f (n)(x0) (dx)n . (2)
Слайд 121Замечания.
1) Скобки в правой части формулы (2) обычно опускают, т.е. записывают
ее в виде:
d ny(x0) = f (n)(x0) dxn . (3)
2) Из формулы (3) получаем, что n-я производная
y(n) = f (n)(x) является отношением 2-х дифференциалов: Таким образом, символическая дробь превратилась в реальную дробь.
3) Дифференциалы порядка n (n > 1) не обладают свойством инвариантности. Т.е. формула (3) не будет верной, если x – функция.
Слайд 122§4. Использование производной
при вычислении пределов
ТЕОРЕМА 1 (Правило Лопиталя).
Пусть x0ℝ̄ и выполняются следующие условия:
1) функции f(x) и (x) определены
и непрерывны в некоторой -окрестности x0, за исключением возможно самой x0;2)
3) функции f(x) и (x) дифференцируемы в U*(x0,) , причем
(x) 0 , xU*(x0,) .
Тогда, если (конечный или бесконечный),
то причем эти два предела будут равны. Т.е.
Слайд 123Замечания.
1) Если f (x) и (x) тоже являются б.м. (б.б.) при
x x0 , то правило Лопиталя можно применить повторно.
2) Если
не существует, то правило Лопиталя непри-менимо. При этом может существовать.
ПРИМЕР. Найти
Слайд 124§5. Исследование функций и построение графиков
1. Возрастание и убывание функции
ОПРЕДЕЛЕНИЕ. Функция y = f(x) называется возрастающей (неубывающей) на интервале (a;b) если
x1,x2(a;b) таких, что x1 < x2 выполняется неравенствоf(x1) < f(x2) ( f(x1) f(x2) ).
Иначе говоря, функция y = f(x) называется возрастающей на (a;b), если большему значению аргумента из (a;b) соответ- ствует большее значение функции.
Функция y = f(x) называется убывающей (невозрастающей) на интервале (a;b) если x1,x2(a;b) таких, что x1 < x2 выполняется неравенство
f(x1) > f(x2) ( f(x1) f(x2) ).
Иначе говоря, функция y = f(x) называется убывающей на (a;b), если большему значению аргумента из (a;b) соответ- ствует меньшее значение функции.
Слайд 125Интервалы возрастания и убывания функции называются интервалами монотонности функции.
ТЕОРЕМА 1(необходимое
и достаточное условия возрастания (убывания) функции).
Пусть y = f(x) дифференцируема на
интервале (a;b). Тогда1) если y = f(x) возрастает (убывает) на (a;b), то на этом интервале ее производная неотрицательна (неположи- тельна), т.е. f (x) 0 , x(a;b) ( f (x) 0 , x(a;b) );
(необходимое условие возрастания (убывания) функции)
2) если f (x) > 0 , x(a;b) ( f (x) < 0 , x(a;b) ) ,
то функция y = f(x) на (a;b) возрастает (убывает).
(достаточное условие возрастания (убывания) функции)
Слайд 1262. Экстремумы функции
Пусть x0D(f ), x0 – внутренняя точка D(f
) (т.е. существует не- которая окрестность точки x0 , целиком лежащая во
мно- жестве D(f )).ОПРЕДЕЛЕНИЕ. Точка x0 называется точкой максимума функции f(x) если существует такая -окрестность U(x0,) точки x0, что f(x) < f(x0) , xU*(x0,).
Значение функции точке максимума называется максимумом функции.
Точка x0 называется точкой минимума функции f(x) если существует такая -окрестность U(x0,) точки x0, что f(x) > f(x0) , xU*(x0,).
Значение функции точке минимума называется минимумом функции.
Точки минимума и максимума функции называются ее точками экстремума.
Минимумы и максимумы функции называются ее экстре- мумами.
Слайд 127Замечания:
1) Понятия минимум и максимум функции близки к понятиям наименьшее
и наибольшее значения функции. Они показывают, в каком отношении находятся
значение функции в точке x0 и в других точках.Различие – в области действия понятий. Наибольшее и наименьшее значения – понятия глобального характера, максимум и минимум – понятия локального характера.
Поэтому в некоторой литературе употребляют термины «глобальный максимум (минимум)» вместо наибольшего (наименьшего) значения функции и «локальный максимум (минимум)» – вместо максимум (минимум) функции.
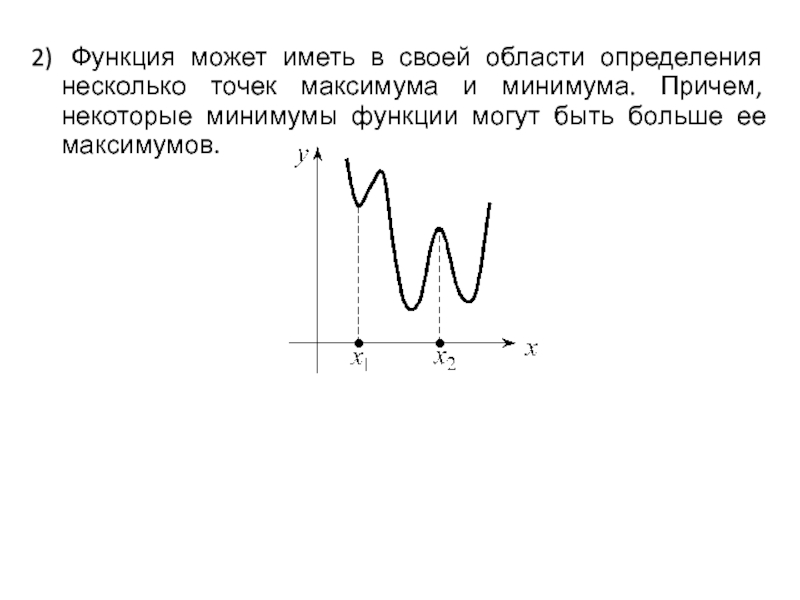
Слайд 1282) Функция может иметь в своей области определения несколько точек максимума
и минимума. Причем, некоторые минимумы функции могут быть больше ее
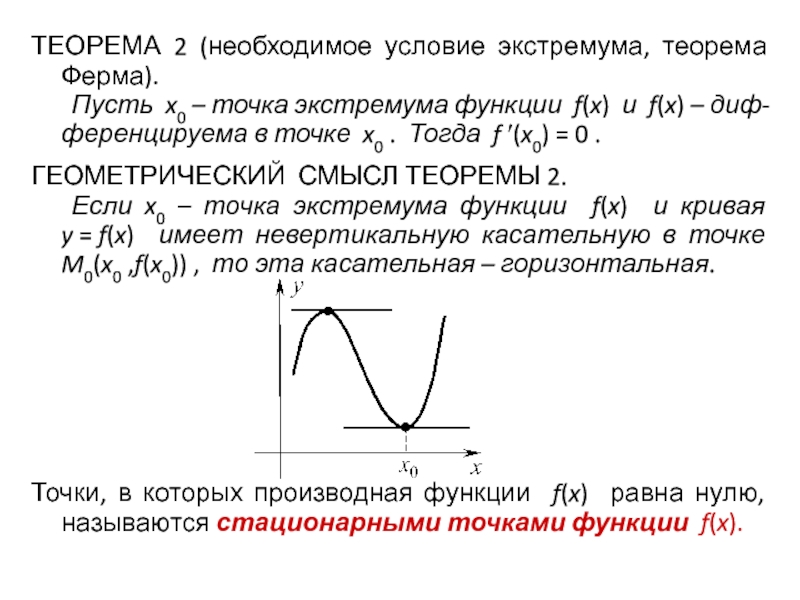
максимумов.Слайд 129ТЕОРЕМА 2 (необходимое условие экстремума, теорема Ферма).
Пусть x0 –
точка экстремума функции f(x) и f(x) – диф- ференцируема в точке
x0 . Тогда f (x0) = 0 .ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ТЕОРЕМЫ 2.
Если x0 – точка экстремума функции f(x) и кривая y = f(x) имеет невертикальную касательную в точке M0(x0 ,f(x0)) , то эта касательная – горизонтальная.
Точки, в которых производная функции f(x) равна нулю, называются стационарными точками функции f(x).
Слайд 130ТЕОРЕМА 3 (достаточное условие экстремума).
Пусть x0 – внутренняя точка
D(f) ,
f(x) непрерывна в U(x0,)
f(x) дифференцируема в U(x0,) или
U*(x0,) . Если при переходе через точку x0 производная функции f(x) меняет знак, то x0 является точкой экстремума.
При этом, если производная меняет знак с плюса на минус, то x0 – точка максимума, если с минуса на плюс – то x0 – точка минимума.
Замечание.
Из теоремы 3 точками экстремума могут быть не только стационарные точки, но и точки, в которых функция не имеет производной (точки разрыва производной).
Стационарные точки функции f(x) и точки, в которых f (x) не существует, называются критическими точками I рода (критическими точками по первой производной).
Слайд 1313. Выпуклость и вогнутость кривой.
Точки перегиба
ОПРЕДЕЛЕНИЕ. Пусть ℓ
– кривая, M0 – точка кривой, причем в M0 существует
невертикальная касательная к ℓ.Кривую ℓ называют выпуклой в точке M0, если в некоторой окрестности этой точки кривая лежит ниже касательной, проведенной к ℓ в точке M0.
Кривую ℓ называют вогнутой в точке M0, если в некоторой окрестности этой точки кривая лежит выше касательной, проведенной к ℓ в точке M0.
Слайд 132Точки кривой, которые разделяют ее выпуклые и вогнутые участки, называются
точками перегиба кривой.
Замечания.
1) Выпуклость и вогнутость кривой в точке
– локальные понятия. Они определяют относительное расположение точек кривой и касательной вблизи точки касания. В точках, удаленных от точки касания, кривая и касательная могут располагаться произвольным образом.2) В точке перегиба касательная к кривой (если она существует) пересекает кривую (кривая переходит с одной стороны касательной на другую).
Слайд 133ОПРЕДЕЛЕНИЕ. Кривая y = f(x) называется выпуклой (вогнутой) на интервале (a;b) если
x(a;b) кривая выпукла (вогнута) в соответствующей точке M(x ; f(x)).
Замечания.
1) Если M0(x0 ; f(x0)) –
точка перегиба кривой y = f(x), то x0 – внутренняя точка области определения функции f(x). 2) Точками перегиба кривой y = f(x) часто называют точки, которые разделяют интервалы выпуклости и вогнутости этой кривой (т.е. абсциссы точек перегиба кривой y = f(x)).
Слайд 134ТЕОРЕМА 5 (необходимое и достаточное условия выпуклости (вогнутости) графика функции).
Пусть функция y = f(x) дважды дифференцируема на интервале (a;b). Тогда:
1) если
кривая y = f(x) выпукла (вогнута) на интервале (a;b), то f (x) 0 (f (x) 0), x(a;b)(необходимое условие выпуклости (вогнутости) кривой);
2) если f (x) < 0 (f (x) > 0) x(a;b),
то кривая y = f(x) выпукла (вогнута) на интервале (a;b)
(достаточное условие выпуклости (вогнутости) кривой).
Слайд 135СЛЕДСТВИЕ 6 (необходимое условие перегиба кривой y = f(x)).
Пусть функция y = f(x)
дважды дифференцируема в U(x0,) (или в U*(x0,) ).
Если M0(x0 ; f(x0)) –
точка перегиба кривой y = f(x), то f (x0) = 0 или в точке x0 функция y = f(x) не имеет второй производной.Замечание. Точки, в которых вторая производная функции y = f(x) обращается в ноль или имеет разрыв, называют иногда критическими точками II рода функции y = f(x) (или критическими точками функции y = f(x) по второй производной).
ТЕОРЕМА 7 (достаточное условие перегиба кривой y = f(x)).
Пусть x0 – внутренняя точка D(f ) и функция f(x) дважды дифференцируема в U*(x0,).
Если при переходе через точку x0 функция f (x) меняет знак, то точка M0(x0 ; f(x0)) является точкой перегиба кри- вой y = f(x).
Слайд 1364. Асимптоты кривой
ОПРЕДЕЛЕНИЕ. Прямая ℓ называется асимптотой кривой, если
при неограниченном удалении точки M кривой от начала координат расстояние
от точки M до прямой ℓ стремится к нулю.Замечание.
Выделяют два вида асимптот: вертикальные и наклонные.
Вертикальные асимптоты кривая y = f(x) не пересекает (почему?), наклонные – может пересекать.
Слайд 137ТЕОРЕМА 8 (необходимое и достаточное условие существова- ния наклонной асимптоты кривой
y = f(x)).
Прямая y = kx + b является наклонной асимптотой кривой y = f(x) существуют конечные
пределы(или ).
Замечания.
1) Из теоремы 8 следует, что график функции y = f(x) может иметь наклонную асимптоту только если функция определена в окрестности + или – .
Причем, наклонных асимптот у кривой y = f(x) может быть не более двух: для правой ветви (т.е. при x +) и для левой ветви (т.е. при x –).
2) Если ,
то наклонная асимптота имеет уравнение y = b, т.е. является горизонтальной.
Слайд 138ТЕОРЕМА 9 (необходимое и достаточное условие существова- ния вертикальной асимптоты кривой
y = f(x)).
Прямая x = a является вертикальной асимптотой кривой y = f(x) точка x = a
является точкой разрыва II рода функции y = f(x), причем, хотя бы один из односторонних пределов f(a – 0), f(a + 0) равен бесконечности.Слайд 139СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ
Найти область определения функции.
Исследовать четность и периодичность
функции.
Исследовать точки разрыва, найти вертикальные асимптоты.
Найти наклонные асимптоты (если их
существование возможно).Найти точки пересечения графика с осями координат.
Найти f (x) . Определить точки экстремума, интервалы воз- растания и убывания функции.
Найти f (x). Определить точки перегиба графика, интервалы его выпуклости и вогнутости.
Построить график функции.