Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Содержание
- 1. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
- 2. Область определения, интервалы варьирования и уровни факторовОбластью
- 3. Область определения, интервалы варьирования и уровни факторовПосле
- 4. Область определения, интервалы варьирования и уровни факторовШаг
- 5. Область определения, интервалы варьирования и уровни факторовРазмер
- 6. Область определения, интервалы варьирования и уровни факторовРекомендации по выбору интервалов варьирования факторов
- 7. Область определения, интервалы варьирования и уровни факторовРекомендации по выбору интервалов варьирования факторов
- 8. Область определения, интервалы варьирования и уровни факторовРекомендации по выбору интервалов варьирования факторов
- 9. Область определения, интервалы варьирования и уровни факторовЭксперимент,
- 10. Область определения, интервалы варьирования и уровни факторовВведем
- 11. Полный факторный экспериментИтак, с помощью полного факторного
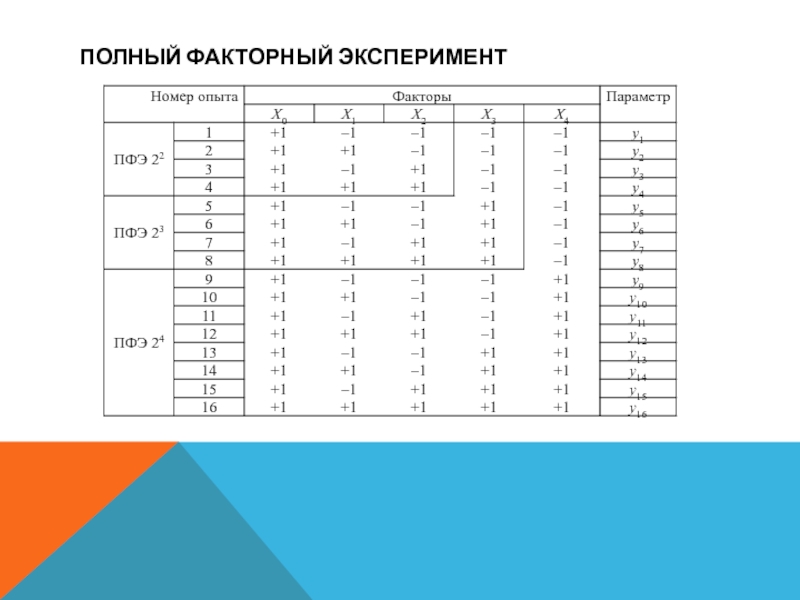
- 12. Полный факторный экспериментВ табл. приведены условия опытов
- 13. Полный факторный экспериментПлан эксперимента принято составлять в
- 14. Полный факторный эксперимент
- 15. Полный факторный экспериментФактор X0 – фиктивный и
- 16. Полный факторный эксперимент2. Свойство нормировки – каждый
- 17. Полный факторный экспериментРассмотрим снова матрицу планирования 22.
- 18. Полный факторный эксперимент
- 19. Полный факторный экспериментКоэффициенты при переменных указывают на
- 20. Полный факторный экспериментДля оценки эффекта взаимодействия матрица
- 21. Используемая литература1. Основы научных исследований. Курс лекций
- 22. Скачать презентанцию
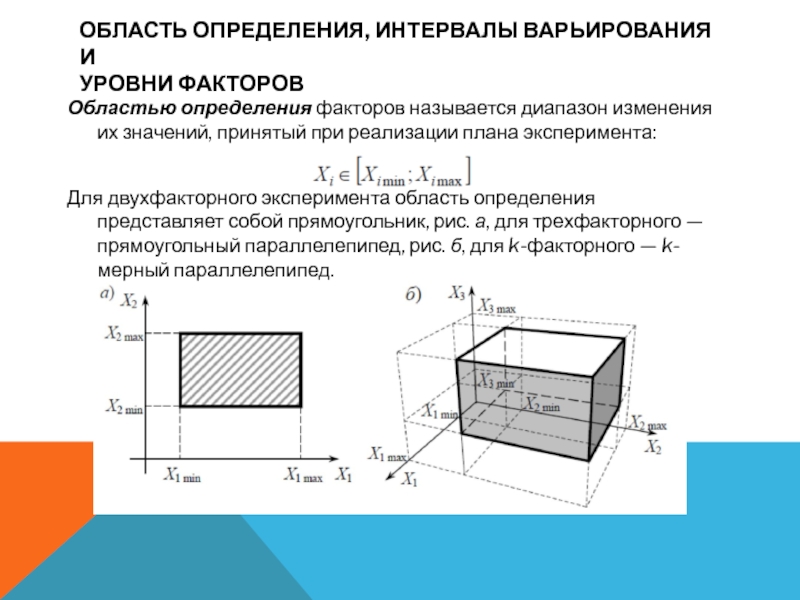
Область определения, интервалы варьирования и уровни факторовОбластью определения факторов называется диапазон изменения их значений, принятый при реализации плана эксперимента:Для двухфакторного эксперимента область определения представляет собой прямоугольник, рис. а, для трехфакторного —
Слайды и текст этой презентации
Слайд 2Область определения, интервалы варьирования и
уровни факторов
Областью определения факторов называется диапазон
изменения их значений, принятый при реализации плана эксперимента:
область определения представляет собой прямоугольник, рис. а, для трехфакторного — прямоугольный параллелепипед, рис. б, для k-факторного — k-мерный параллелепипед.Слайд 3Область определения, интервалы варьирования и
уровни факторов
После выявления значимых факторов области
их определения устанавливают их уровни. Уровнем фактора называется его значение,
фиксируемое в эксперименте.Различают верхний, нижний и нулевой уровни. Верхний и нижний уровни соответствуют границам области определения: Xi max и Xi min. Нулевой уровень соответствует середине интервала.
Интервалом варьирования называют величину, равную максимальному отклонению уровня фактора от нулевого:
Слайд 4Область определения, интервалы варьирования и
уровни факторов
Шаг (интервал) варьирования по каждой
переменной выбирается таким, чтобы приращение величины выходного параметра y к
базовому значению y* при реализации шага можно было выделить на фоне «шума» при небольшом числе параллельных опытов.Если нет никаких указаний на величину шага xi, то в первом приближении можно выбрать xi = 0,15x0i, т.е. принять за шаг 15 % - ное отклонение от базового уровня x0i. Такой шаг предоставляет достаточную гарантию того, что фактор xi вызовет заметную реакцию y, если связь между ними существует.
Слайд 5Область определения, интервалы варьирования и
уровни факторов
Размер интервала варьирования определяется многими
факторами, но упрощенно можно ограничиться следующим:
если интервал составляет менее 10
% от области определения, он считается узким; если не более 30 % – средним; более 30 % – широким.Точность фиксирования (определения) факторов определяется точностью приборов и стабильностью в ходе опыта. Упрощенно можно полагать, что если погрешность составляет:
< 1 % – высокая точность,
< 5 % – средняя точность,
>10 % – низкая точность эксперимента.
Слайд 6Область определения, интервалы варьирования и
уровни факторов
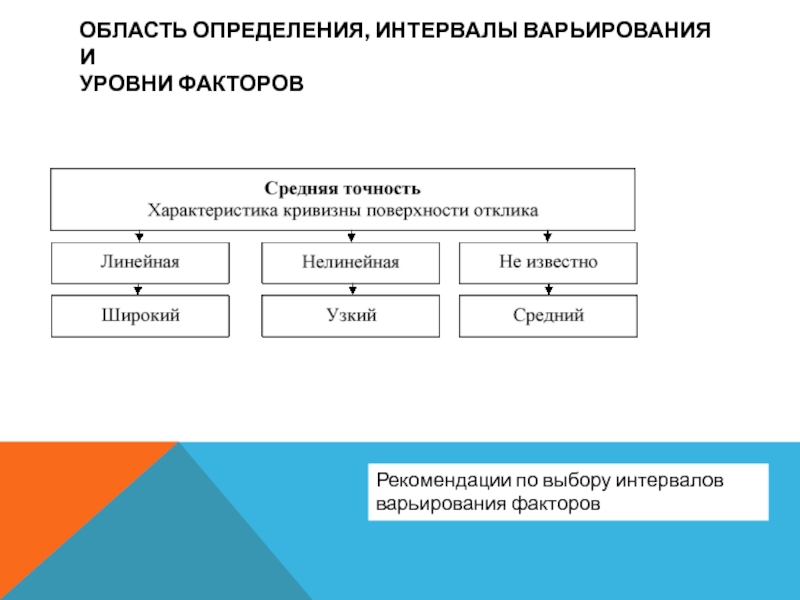
Рекомендации по выбору интервалов варьирования
факторов
Слайд 7Область определения, интервалы варьирования и
уровни факторов
Рекомендации по выбору интервалов варьирования
факторов
Слайд 8Область определения, интервалы варьирования и
уровни факторов
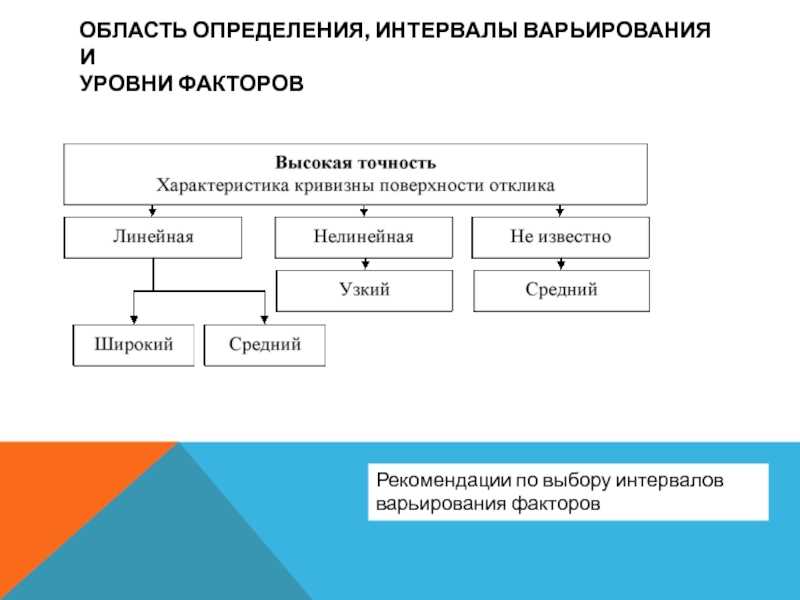
Рекомендации по выбору интервалов варьирования
факторов
Слайд 9Область определения, интервалы варьирования и
уровни факторов
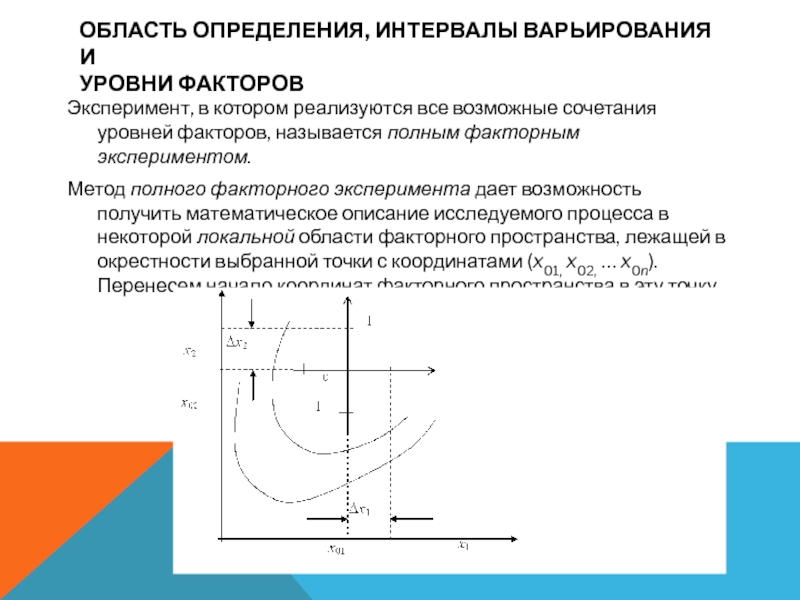
Эксперимент, в котором реализуются все
возможные сочетания уровней факторов, называется полным факторным экспериментом.
Метод полного
факторного эксперимента дает возможность получить математическое описание исследуемого процесса в некоторой локальной области факторного пространства, лежащей в окрестности выбранной точки с координатами (x01, x02, … x0n). Перенесем начало координат факторного пространства в эту точкуСлайд 10Область определения, интервалы варьирования и
уровни факторов
Введем новые переменные:
где xi
– масштаб по оси xi.
Иногда величину Xi называют кодированной переменной.
Метод полного факторного эксперимента служит для получения математического описания процесса в виде отрезка ряда Тейлора.
Следует отметить, что коэффициенты искомого уравнения определяются на основе экспериментальных данных и, следовательно, несут на себе отпечаток погрешностей эксперимента. Чтобы подчеркнуть это обстоятельство, в уравнении вместо символов , обозначающих истинные значения коэффициентов, пишут b, подразумевая под этим соответствующие выборочные оценки.
Слайд 11Полный факторный эксперимент
Итак, с помощью полного факторного эксперимента ищут математическое
описание процесса в виде уравнения
Его называют уравнением регрессии, а входящие
в него коэффициенты – коэффициентами регрессии. В планировании экспериментов используются, в основном, планы первого и второго порядков.
Для удобства вычислений коэффициентов регрессии все факторы в ходе полного факторного эксперимента варьируют на двух уровнях, соответствующих значениям кодированных переменных +1 и –1.
Слайд 12Полный факторный эксперимент
В табл. приведены условия опытов полного двухфакторного эксперимента.
Опыты, приведенные в табл. соответствуют на факторной плоскости вершинам квадрата
с центром в начале координат.Слайд 13Полный факторный эксперимент
План эксперимента принято составлять в виде матрицы планирования
— таблицы, каждая строка которой соответствует некоторому сочетанию уровней факторов,
которое реализуется в опыте.Существует несколько приемов построения матрицы. При фиксации каждого фактора только на двух уровнях (–1 и +1), наиболее распространен прием чередования знаков.
Прием состоит в том, что для первого фактора знак меняется в каждой следующей строке, для второго — через строку, для третьего — на каждой четвертой строке и т.д. Построенные таким образом матрицы для двух, трех и четырех факторов приведены в табл.
Слайд 15Полный факторный эксперимент
Фактор X0 – фиктивный и введен для удобства
определения свободного члена полинома b0. Значение фактора X0 всегда равно
+1.Матрицы ПФЭ обладают рядом свойств, позволяющих проверить правильность их составления:
Свойство симметричности – каждый фактор в матрице на верхнем уровне встречается столько же раз, сколько и на нижнем (алгебраическая сумма элементов вектор – столбца каждого фактора равна нулю)
где j – номер фактора;
N – число опытов.
Слайд 16Полный факторный эксперимент
2. Свойство нормировки – каждый фактор в матрице
встречается только на уровнях –1 и +1 (сумма квадратов элементов
каждого столбца равна числу опытов)3. Свойство ортогональности – суммы почленных произведений двух любых столбцов равны нулю
4. Свойство ротабельности – точки в матрице выбираются так, что точность предсказания параметра одинакова во всех направлениях.
Слайд 17Полный факторный эксперимент
Рассмотрим снова матрицу планирования 22. Предположим, что для
движения к оптимуму нужна линейная модель типа y = b0
+ b1X1 + b2X2.Наша задача – найти неизвестные коэффициенты, причем эксперимент, содержащий конечное число опытов, позволяет получить только выборочные оценки для коэффициентов уравнения. Их точность зависит от свойств выборки и нуждается в статистической проверке.
Оценки коэффициентов вычисляются по простой формуле
Слайд 19Полный факторный эксперимент
Коэффициенты при переменных указывают на силу влияния факторов.
Чем больше коэффициент по абсолютной величине, тем больше влияние на
эксперимент оказывает данный фактор.Знак плюс говорит о том, что параметр оптимизации увеличивается с увеличением фактора, минус – наоборот.
Планируя эксперимент на первом этапе, мы стремимся получить линейную модель. Однако у нас нет гарантии, что в выбранных интервалах варьирования модель линейна. Один из часто встречающихся видов нелинейности связан с тем, что эффект одного фактора зависит от уровня, на котором находится другой фактор, то есть просматривается эффект взаимодействия двух факторов.
Слайд 20Полный факторный эксперимент
Для оценки эффекта взаимодействия матрица планирования 22 дополняется
еще одним столбцом
Дополнительный коэффициент можно представить в виде
Модель будет
выглядеть следующим образом:y = b0 + b1X1 + b2X2 + b12X1X2.