Математика

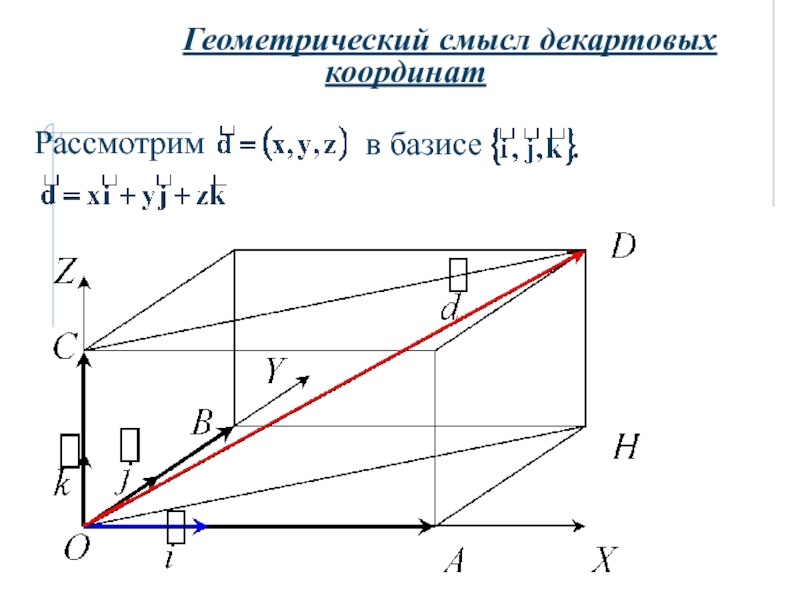
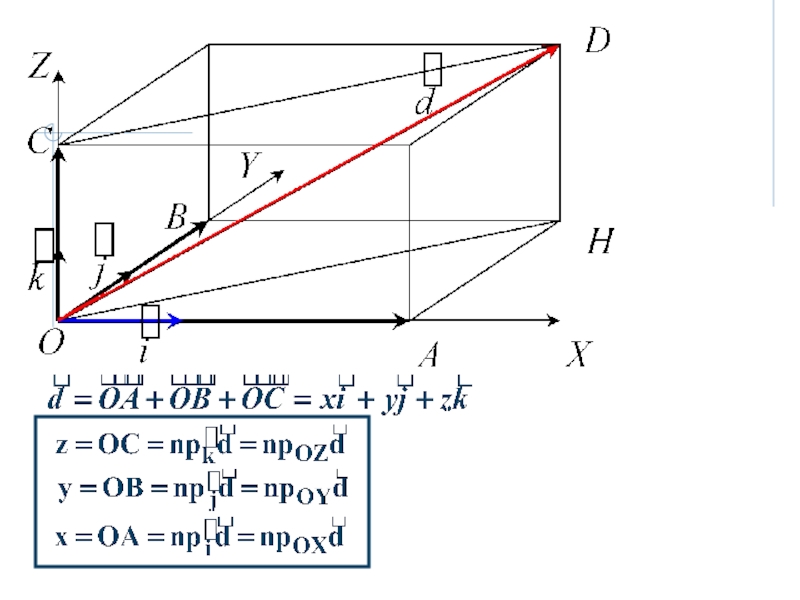
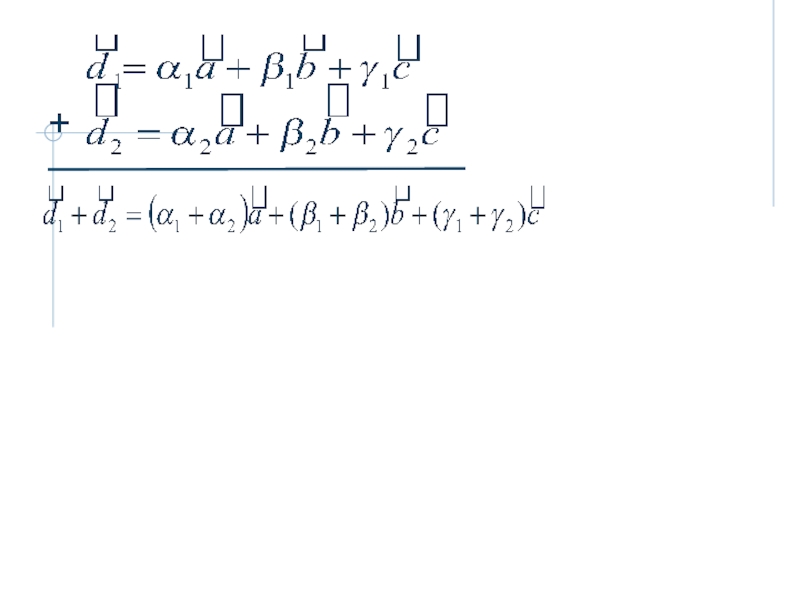3. Линейные операции над векторами, заданными в
координатной

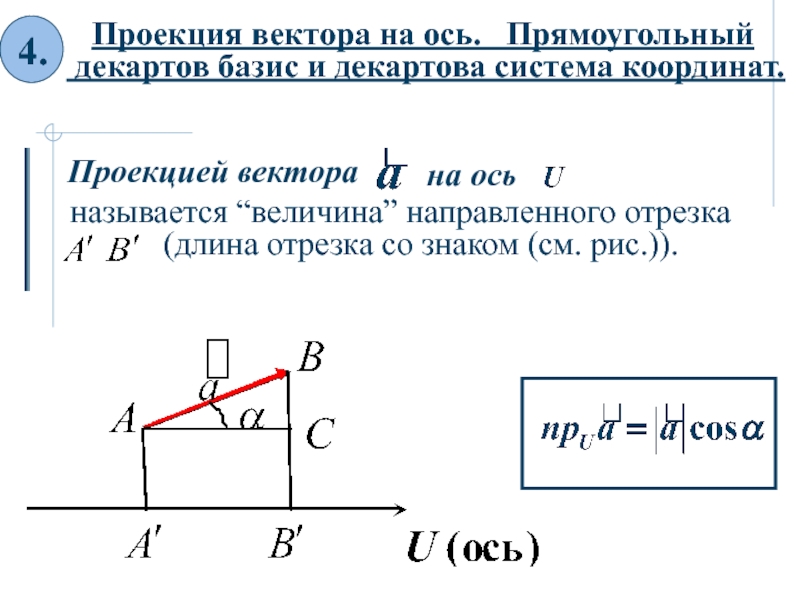
4. Проекция вектора на ось.

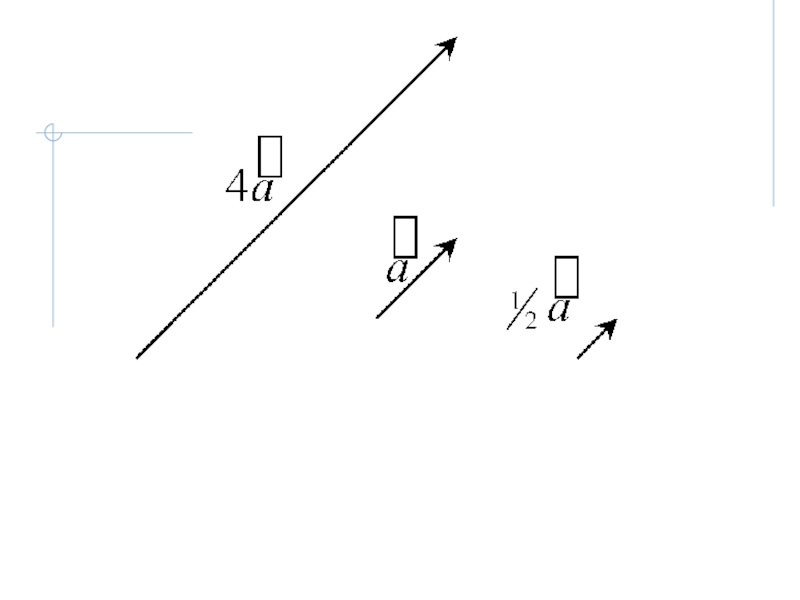
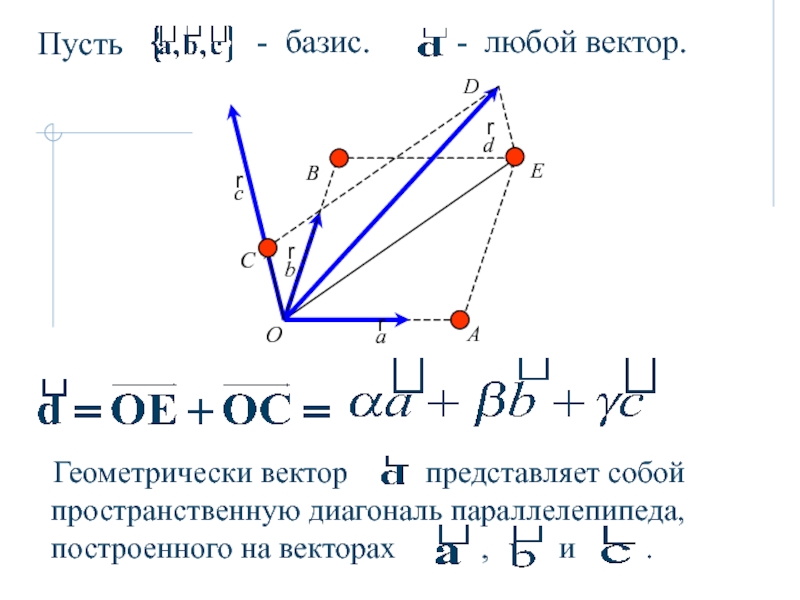
I. Векторы. Линейные операции над векторами.
Линейная зависимость векторов.

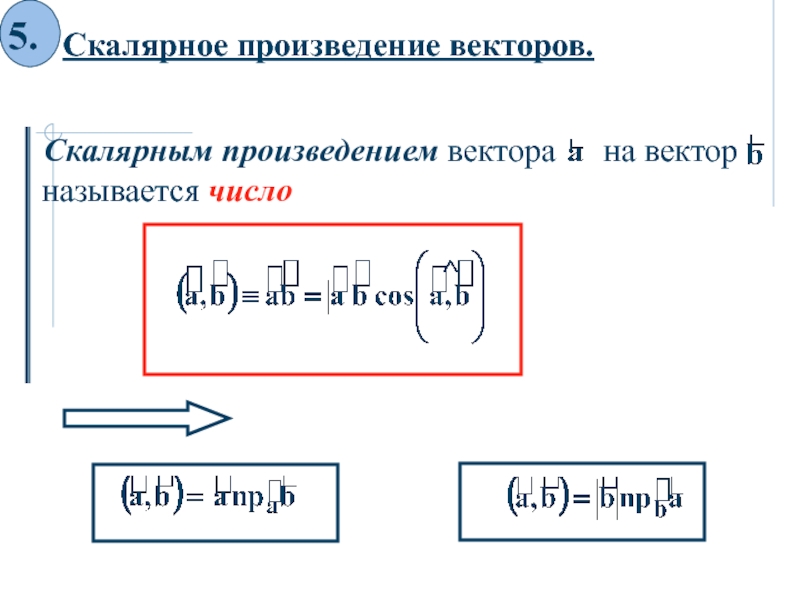
5. Скалярное произведение векторов.

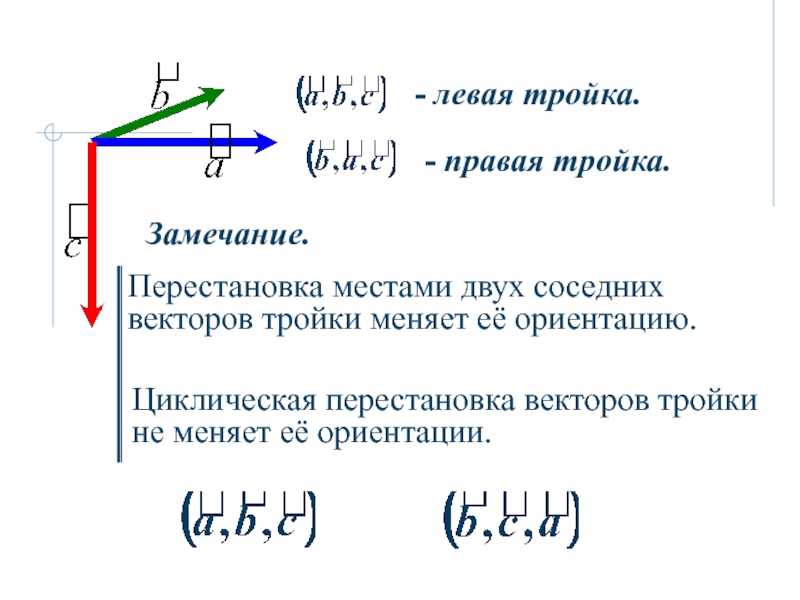
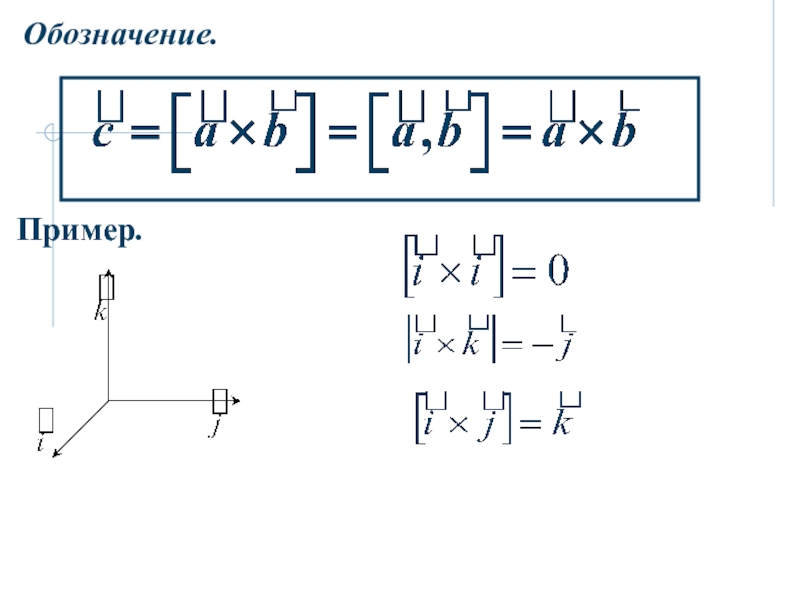
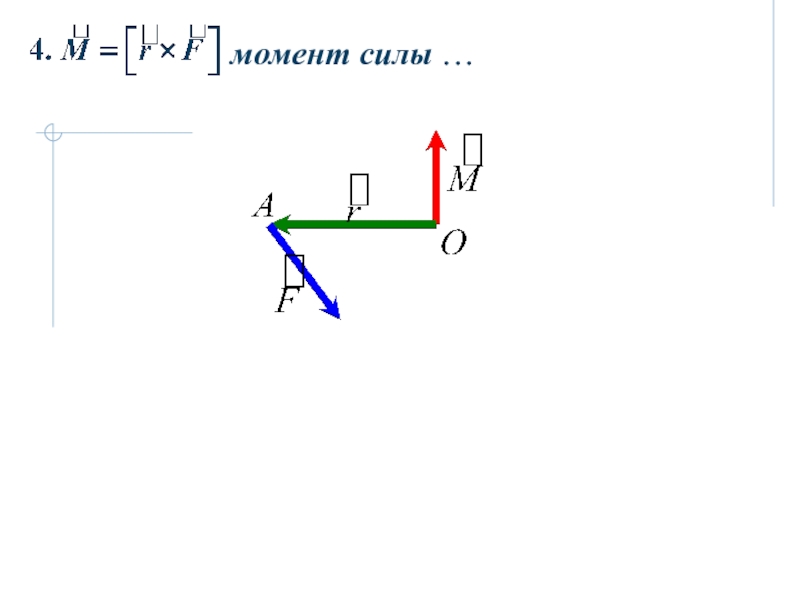
6. Векторное произведение векторов.

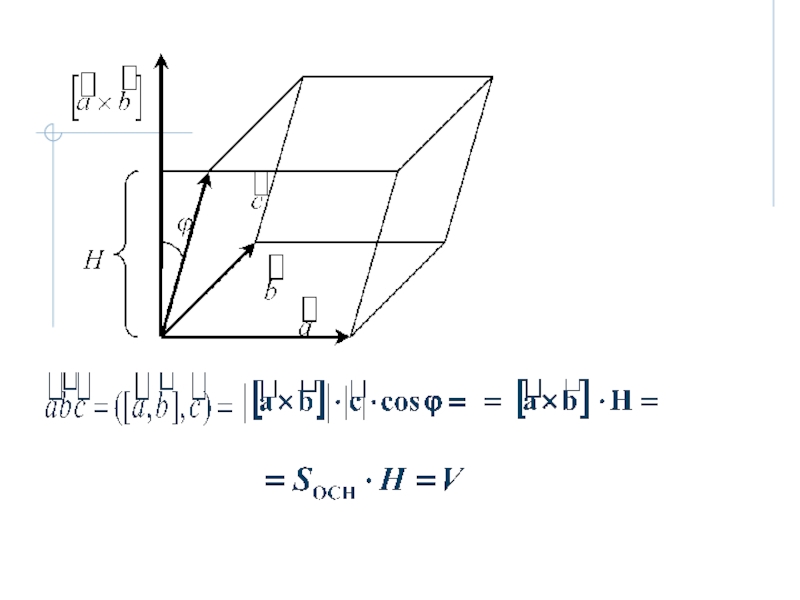
7. Смешанное произведение векторов.

его характеристики – длина и направление.
Базовые определения: нулевой

Линейные операции над векторами.

I. Сложение векторов

Геометрическое определение –
правило треугольника и правило
параллелограмма:

Умножение вектора на число.

(ЛК) векторов называется
сумма их произведений на произвольные числа:

Если

3.

два неколлинеарных вектора этой плоскости.
Базисом множества векторов на прямой называется

вектора.

(длина отрезка со знаком (см. рис.)).

декартовых координат

Пусть

и направление, то есть все характеристики.

произведения .
-длина вектора.
-угол между векторами.
-проекция вектора на вектор.
-работа силы

ко второму вектору виден из конца третьего вектора осуществляющимся против

перестановка векторов тройки
не меняет её ориентации.

связь линейной и угловой скорости …

Доказательство.

их смешанного
произведения.
Вычисление смешанного произведения векторов, заданных декартовыми координатами .
то

является равенство нулю определителя,
строками которого являются координаты этих векторов

Следствие 2.

Необходимым и достаточным условием линейной
зависимости трёх векторов, является равенство нулю
того же определителя.

Свойство смешанного произведения.

Перестановка местами двух соседних сомножителей
меняет знак смешанного произведения, а циклическая
перестановка сомножителей знака не меняет.