Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математика ППИ. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ Лекция № 12 (продолжение)
Содержание
- 1. Математика ППИ. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ Лекция № 12 (продолжение)
- 2. Цели и задачи: Изучить основные
- 3. ВОПРОСЫ ЛЕКЦИИ №121. Метод интегрирования по частям.2. Интегрирование некоторых классов тригонометрических функций.
- 4. Литература[1] Н.С. Пискунов. Дифференциальное и интегральное исчисления.
- 5. УЧЕБНЫЙ ВОПРОС .Интегрирование некоторых классов тригонометрических функций
- 6. Рассмотрим интеграл вида m и n -
- 7. б) б) m и n - неотрицательные
- 8. Вторая разновидность интегралов имеет вид:или Третья разновидность интегралов
- 9.
- 10. Пример.
- 11. Универсальная тригонометрическая подстановка Всякий интеграл
- 12. Слайд 12
- 13. Пример.
- 14. Рассмотрим интегралы видаДля их вычисления используют тригонометрические формулы
- 15. Пример.
- 16. Задание на самостоятельную работу [1] Н.С. Пискунов.
- 17. Математика ППИ. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ Лекция
- 18. ВОПРОСЫ ЛЕКЦИИ №131. Интегрирование рациональных дробей.2.Интегрирование некоторых классов иррациональных функций
- 19. УЧЕБНЫЙ ВОПРОС.Интегрирование рациональных дробей
- 20. Определение. Дробно- рациональной функцией или просто рациональной
- 21.
- 22.
- 23. Слайд 23
- 24.
- 25. Различают четыре типа простейших рациональных дробей:1.
- 26. Интегрирование простейших дробей I и II типов:I.
- 27. Интегрирование простейшей дроби III типаПример. Найти интеграл Решение.
- 28. Теорема. Правильную рациональную дробь
- 29. Метод неопределённых коэффициентов.Рассмотрим случай, когда корни знаменателя
- 30. 1. Дроби справа приводят к общему знаменателю.2.
- 31. Пример. Разложить дробь
- 32. Итак,
- 33. УЧЕБНЫЙ ВОПРОС.Интегрирование некоторых классов иррациональных функций
- 34. Интегрирование некоторых классов иррациональных функцийС помощью
- 35. Слайд 35
- 36. Пример. Найти
- 37. Интеграл
- 38. Интеграл более общего вида
- 39. Пример.2
- 40. Интегрирование дифференциального бинома
- 41. дробное
- 42.
- 43. Пример.
- 44. Слайд 44
- 45. Тригонометрические подстановкиС помощью тригонометрических подстановок интегралы от
- 46. В
- 47. Пример.
- 48. Далее (потерян минус в последнем слагаемом):
- 49. Пример. Можно проинтегрировать по частям:
- 50. Пример.
- 51. Слайд 51
- 52.
- 53. Слайд 53
- 54. Слайд 54
- 55. Понятие об интегралах, не берущихся в элементарных
- 56. Так, например, хотя по теореме существования для
- 57. Заключение. В заключение отметим, что рассмотренные методы и
- 58. Контрольные вопросы:1. В чем заключается метод интегрирования рациональных дробей?2. Универсальная тригонометрическая подстановка.
- 59. Задание на самостоятельную работу [1] Н.С. Пискунов.
- 60. Скачать презентанцию
Цели и задачи: Изучить основные методы интегрирования: интегрирование рациональных дробей, интегрирование некоторых классов тригонометрических и иррациональных функций.
Слайды и текст этой презентации
Слайд 1
Математика ППИ.
НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
Лекция № 12 (продолжение).
Метод интегрирования по частям
в неопределенном интеграле. Интегрирование тригонометрических функций.
Слайд 2Цели и задачи:
Изучить основные методы интегрирования: интегрирование
рациональных дробей, интегрирование некоторых классов тригонометрических и иррациональных функций.
Слайд 3ВОПРОСЫ ЛЕКЦИИ №12
1. Метод интегрирования по частям.
2. Интегрирование некоторых классов
тригонометрических функций.
Слайд 4Литература
[1] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 1. Москва:
Интеграл-Пресс, 2004, с. 340-375.
[3] Б.П. Демидович, В.А. Кудрявцев. Краткий курс
высшей математики. Москва: Издательство АСТ, 2004, с. 229-250.Слайд 6Рассмотрим интеграл вида
m и n - неотрицательные и по
крайней мере одно из них является нечётным. Пусть n –
нечётное, т.е. n=2p+1. ТогдаСлайд 7б) б) m и n - неотрицательные чётные, т.е.
n=2p, m=2q. Тогда
Возведя в степень и раскрыв скобки, получим
слагаемые, содержащие cos 2xв чётных и нечётных степенях. Члены с нечётными степенями интегрируются, как указано в случае а), чётные показатели снова понижаются по тем же формулам.
Слайд 11 Универсальная тригонометрическая подстановка
Всякий интеграл от рациональной функции вида
может
быть сведён к интегралу от рациональной функции.
Для этого используется подстановка
называемая универсальной тригонометрической подстановкой.
Слайд 16Задание на самостоятельную работу
[1] Н.С. Пискунов. Дифференциальное и интегральное исчисления.
Т 1. Москва: Интеграл-Пресс, 2004, с. 340-375.
[3] Б.П. Демидович, В.А.
Кудрявцев. Краткий курс высшей математики. Москва: Издательство АСТ, 2004, с. 229-250.Выучить таблицу основных интегралов.
Слайд 17
Математика ППИ.
НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
Лекция № 13 .
Интегрирование дробно-рациональных функций, иррациональных
функций. Тригонометрические подстановки.
Слайд 18ВОПРОСЫ ЛЕКЦИИ №13
1. Интегрирование рациональных дробей.
2.Интегрирование некоторых классов иррациональных функций
Слайд 20Определение. Дробно- рациональной функцией или просто рациональной дробью называется функция,
равная частному от деления двух многочленов
здесь
- многочлен степени n, - многочлен степени m.
Слайд 25Различают четыре типа простейших рациональных дробей:
1.
2.
3. 4.
При этом A, a, M,N, p, q – действительные числа, многочлен не имеет вещественных корней.
Интегрирование простейших рациональных дробей
Слайд 28Теорема. Правильную рациональную дробь , где
можно единственным образом разложить в сумму простейших дробей:
где
- действительные числа .Слайд 29Метод неопределённых коэффициентов.
Рассмотрим случай, когда корни знаменателя действительные и различные,
т.е. рассмотрим правильную дробь:
Данную дробь можно разложить на простейшие дроби
I типа следующим образомОтметим, что неизвестные коэффициенты простейших дробей можно найти и методом сравнения коэффициентов, который состоит в следующем:
Слайд 301. Дроби справа приводят к общему знаменателю.
2. Приравнивают числители дробей
слева и справа, раскрывают скобки и записывают многочлен в правой
части по убывающим степеням .3. Приравнивая друг другу коэффициенты многочленов левой и правой части при одинаковых степенях , получим систему уравнений для определения коэффициентов.
Слайд 34 Интегрирование некоторых классов иррациональных функций
С помощью тригонометрических подстановок интегралы
от некоторых иррациональных функций приводятся к интегралам от функций, рационально
зависящих от тригонометрических функцийСлайд 45Тригонометрические подстановки
С помощью тригонометрических подстановок интегралы от некоторых иррациональных функций
приводятся к интегралам от функций, рационально зависящих от тригонометрических функций:
А
Б
Слайд 55Понятие об интегралах, не берущихся в элементарных функциях
Как мы видим,
в дифференциальном исчислении, производная от любой элементарной функции есть функция
элементарная. Другое дело операция, обратная дифференцированию, - интегрирование. Можно привести многочисленные примеры таких элементарных функций, первообразные от которых хотя и существуют, но не являются элементарными функциями.Слайд 56 Так, например, хотя по теореме существования для функций
существуют первообразные, но
они не выражаются в элементарных функциях. Несмотря на это, все
эти первообразные хорошо изучены и для них составлены подробные таблицы, помогающие практически использовать эти функции. В дальнейшем мы познакомимся с методами вычисления значений таких функцийСлайд 57Заключение.
В заключение отметим, что рассмотренные методы и приёмы интегрирования не
исчерпывают всех классов аналитически интегрируемых элементарных функций. В то же
время из всего изложенного следует, что техника интегрирования сложнее по сравнению с дифференцированием. Необходимы навыки и изобретательность, которые приобретаются на практике в результате решения большого числа примеровСлайд 58Контрольные вопросы:
1. В чем заключается метод интегрирования рациональных дробей?
2. Универсальная
тригонометрическая подстановка.
Слайд 59Задание на самостоятельную работу
[1] Н.С. Пискунов. Дифференциальное и интегральное исчисления.
Т 1. Москва: Интеграл-Пресс, 2004, с. 340-375.
[3] Б.П. Демидович, В.А.
Кудрявцев. Краткий курс высшей математики. Москва: Издательство АСТ, 2004, с. 229-250.Выучить таблицу основных интегралов.



![Математика ППИ. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ Лекция № 12 (продолжение) Литература[1] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 1. Москва: Интеграл-Пресс, Литература[1] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 1. Москва: Интеграл-Пресс, 2004, с. 340-375.[3] Б.П. Демидович, В.А.](/img/thumbs/7fb70afc0bc0c033ff01e14c9e49a74a-800x.jpg)





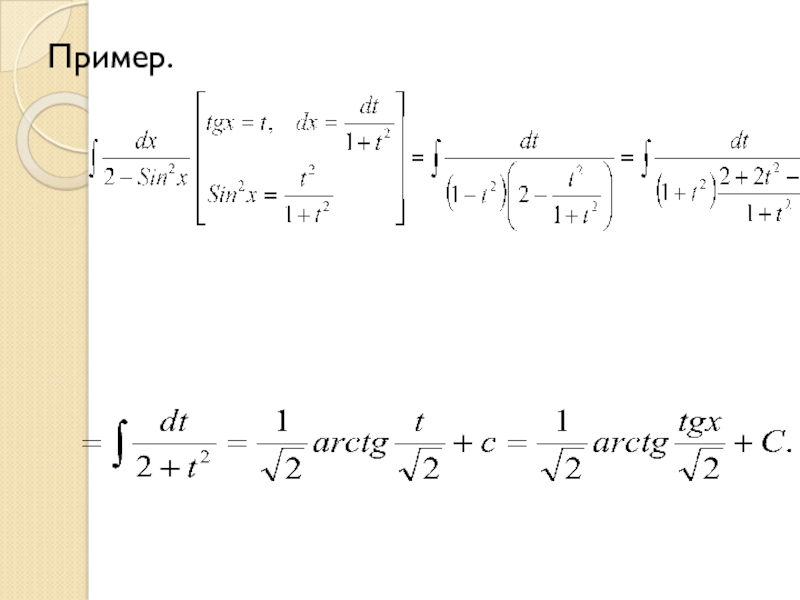

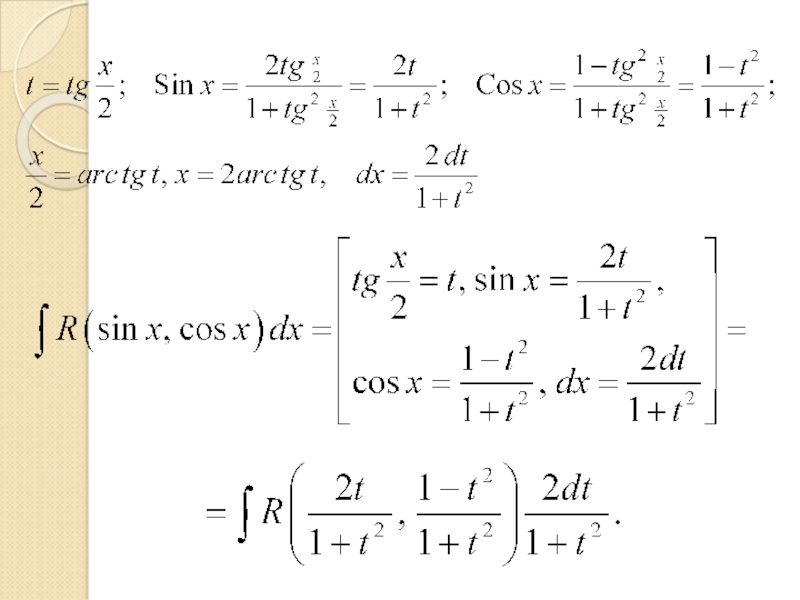



![Математика ППИ. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ Лекция № 12 (продолжение) Задание на самостоятельную работу [1] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Задание на самостоятельную работу [1] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 1. Москва: Интеграл-Пресс, 2004, с.](/img/thumbs/57acca5822c566891417e11db21f08c4-800x.jpg)



























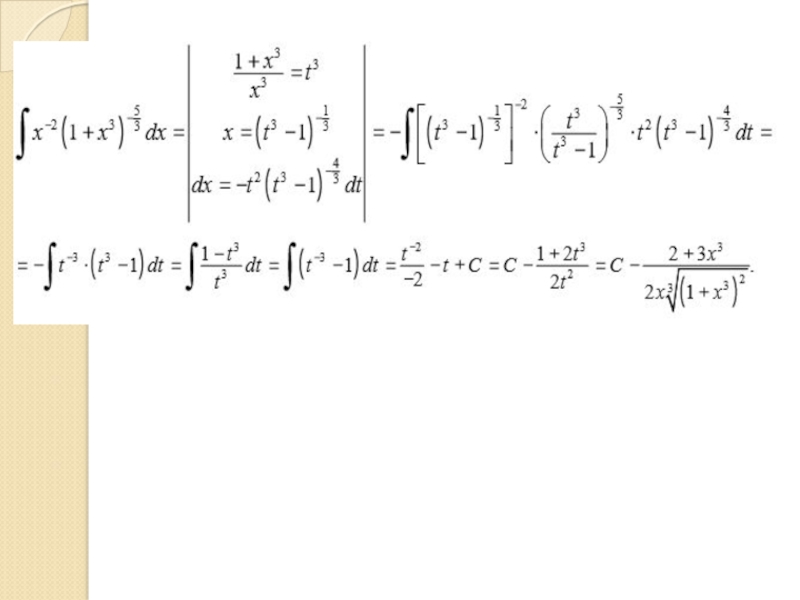

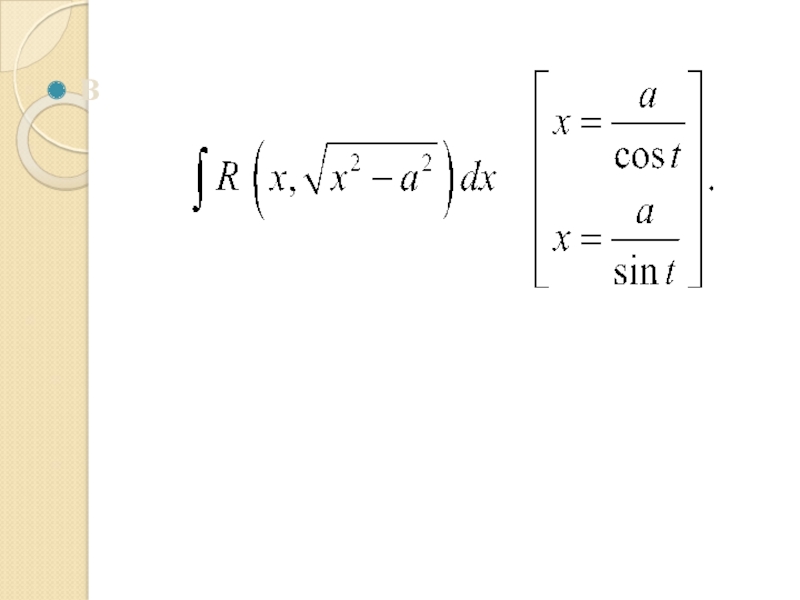











![Математика ППИ. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ Лекция № 12 (продолжение) Задание на самостоятельную работу [1] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Задание на самостоятельную работу [1] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 1. Москва: Интеграл-Пресс, 2004, с.](/img/thumbs/7b05eb29dd8ed5309e93ad1b1316257a-800x.jpg)