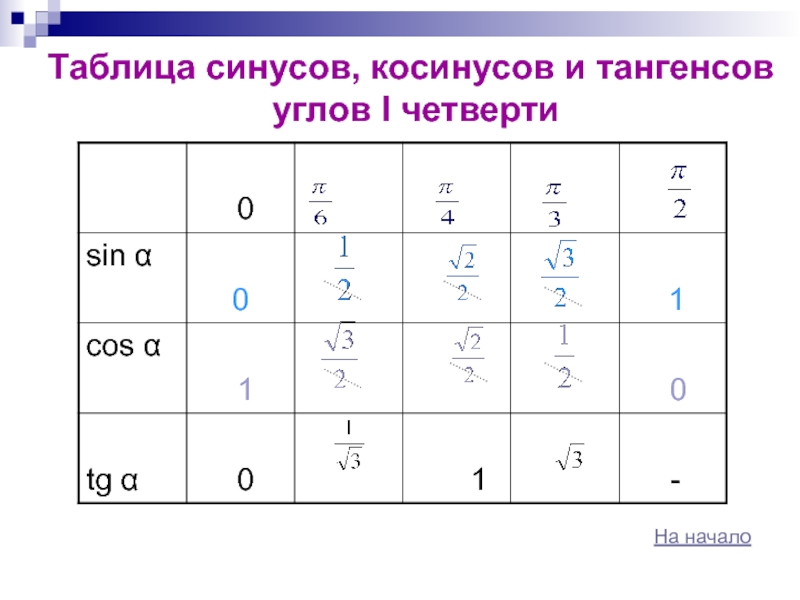
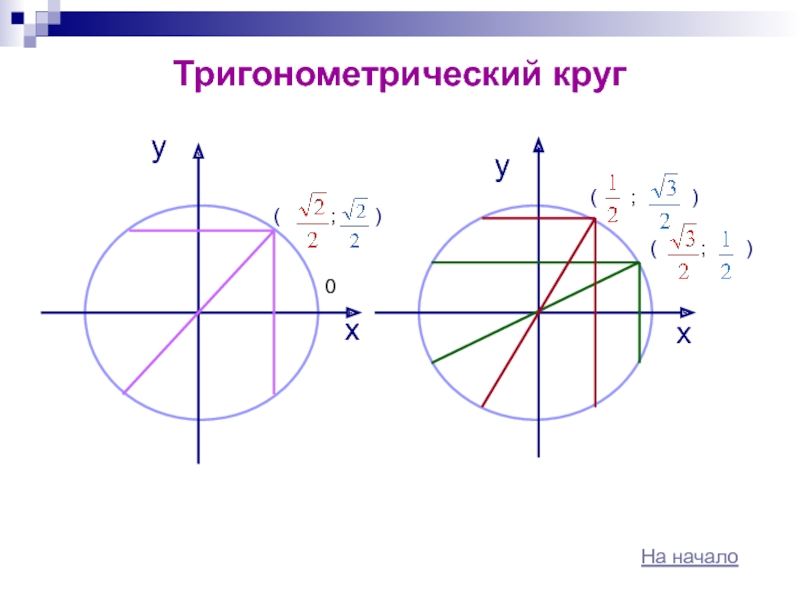
чисел
Умножение Д Д
Деление на Д Д
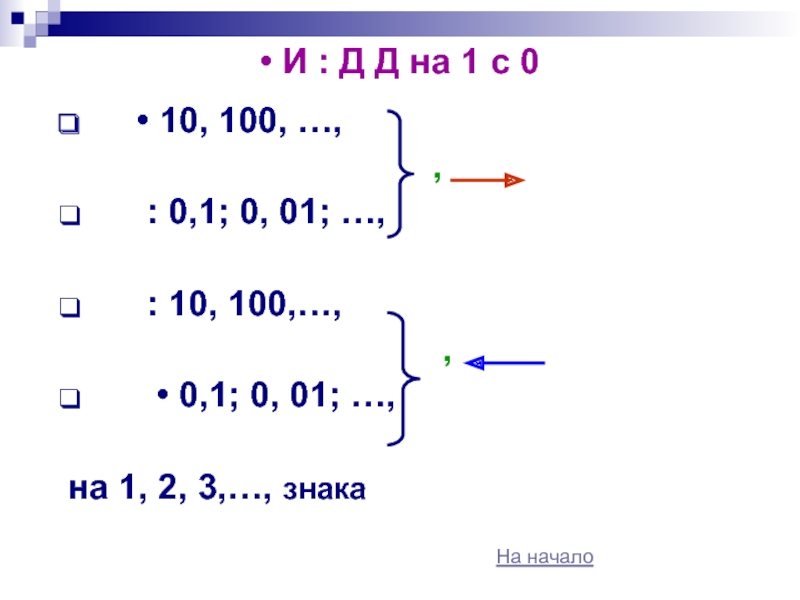
• И : Д Д
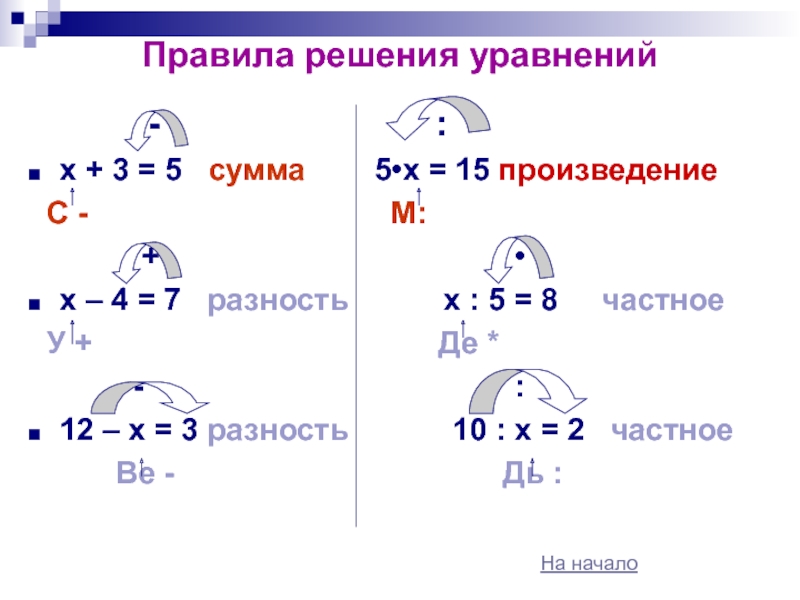
на 1 с 0Правила решения уравнений
Решение уравнений
Процент
Задачи на части
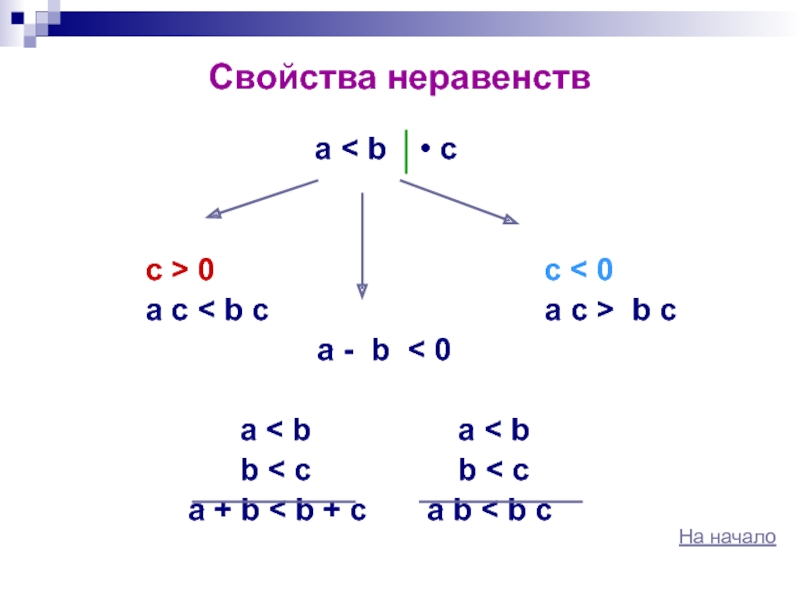
Сравнение чисел
Сложение отрицательных чисел
Сложение чисел с разными знаками
Вычитание
Решение уравнений
Сложение многочленов
Формулы сокращенного умножения
Формулы сокращенного умножения
Свойства степеней
Вынесение общего множителя за скобку
Способ группировки
Разложение на множители по ФСУ