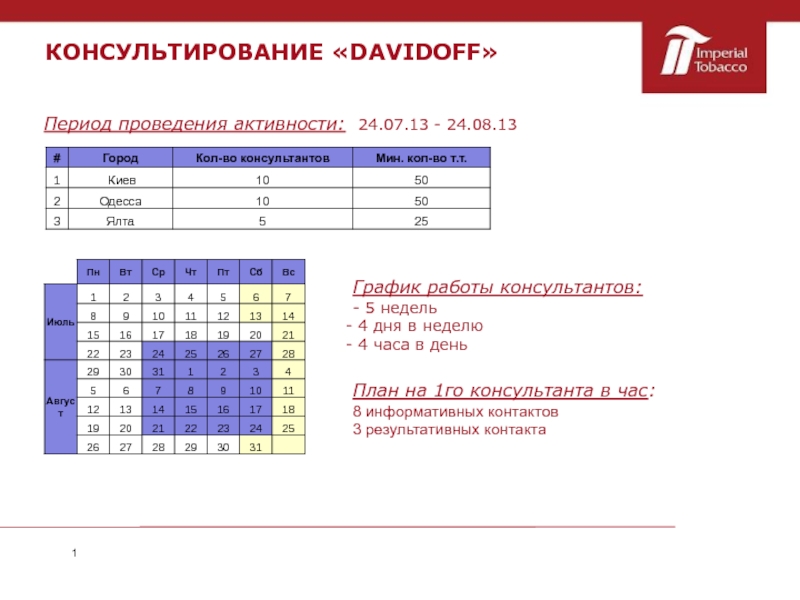
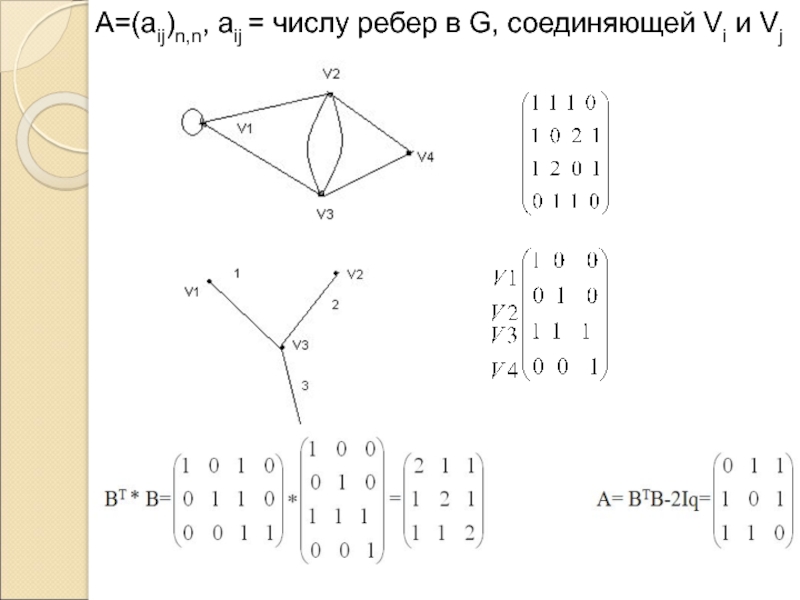
G (ρ(1)=3, ρ(2)=2, ρ(3)=4, ρ(4)=2, ρ(5)=3.
Матрицей смежности (смежностей) А=||aij|| графа
G с p вершинами называется (рxр) матрица, в которой аij = 1, если вершина υi смежна с υj, и аij = 0 в противном случае. Итак, существует взаимно однозначноесоответствие между графами с р вершинами и симметрическими бинарными (рxр) – матрицами с нулями на главной диагонали.




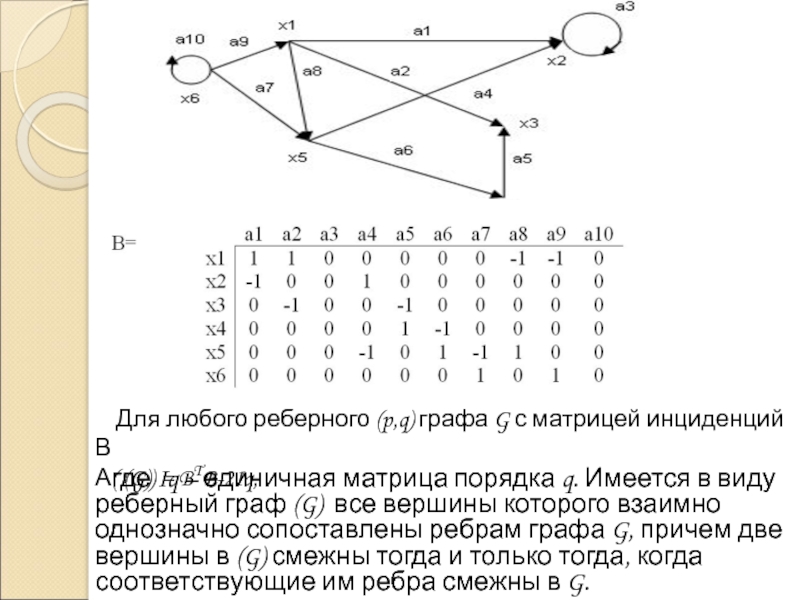
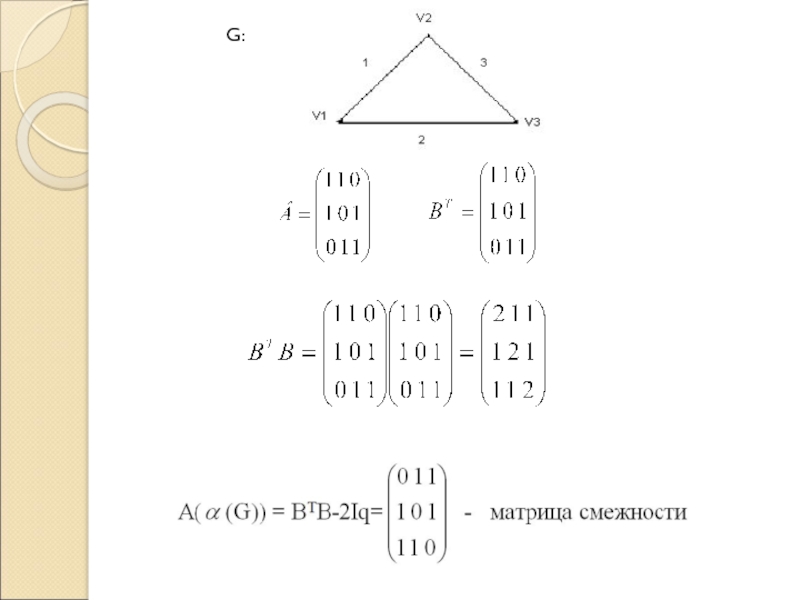
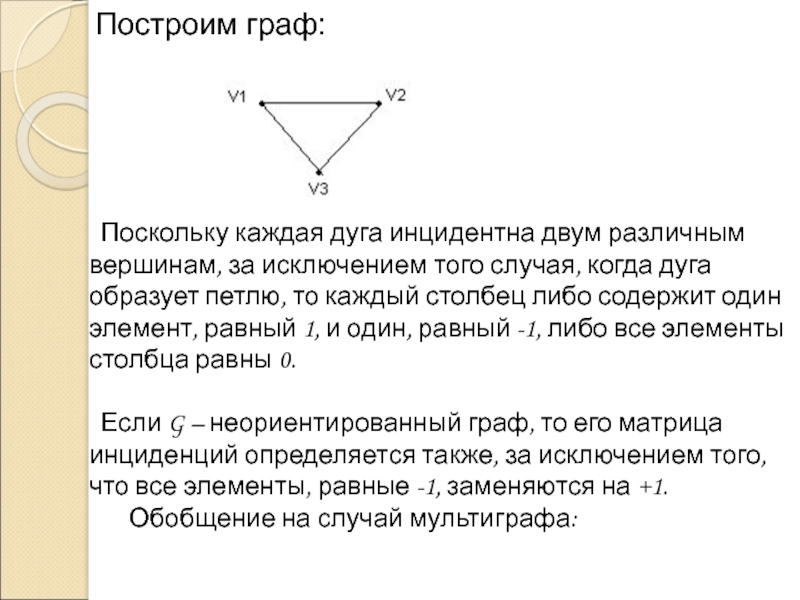
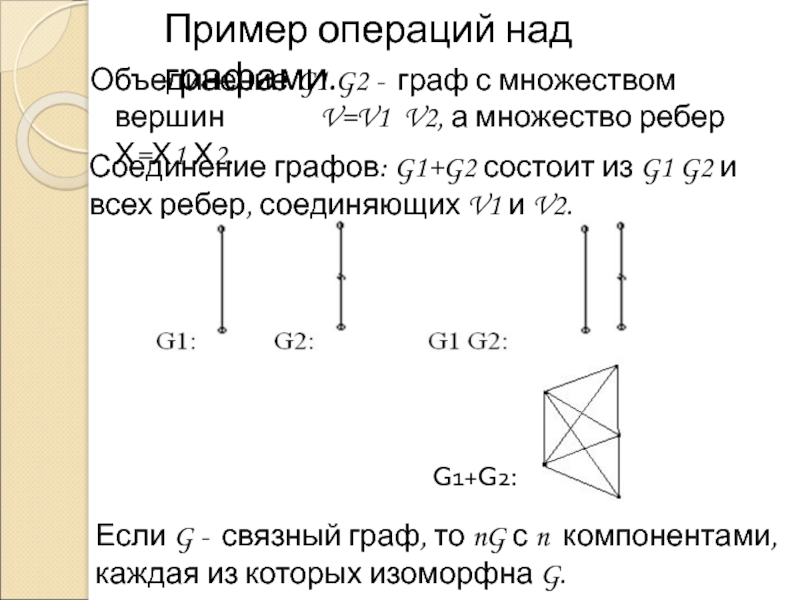
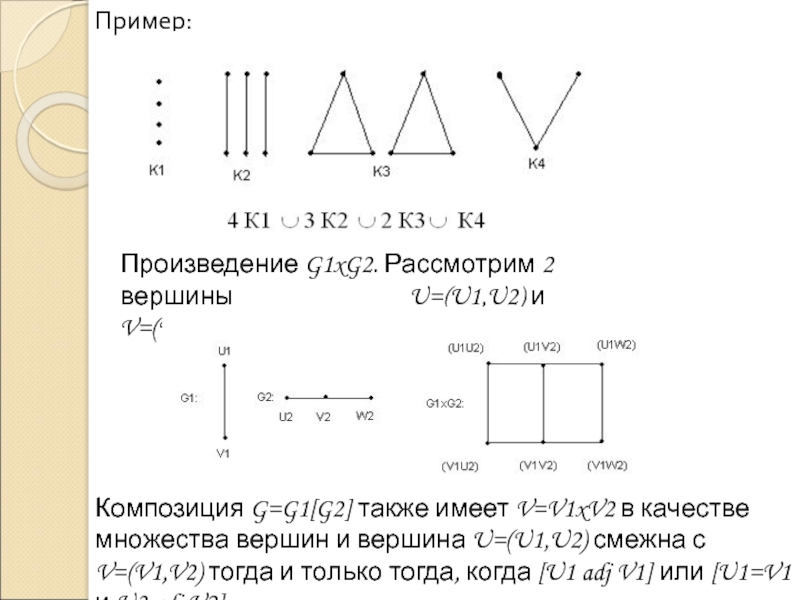
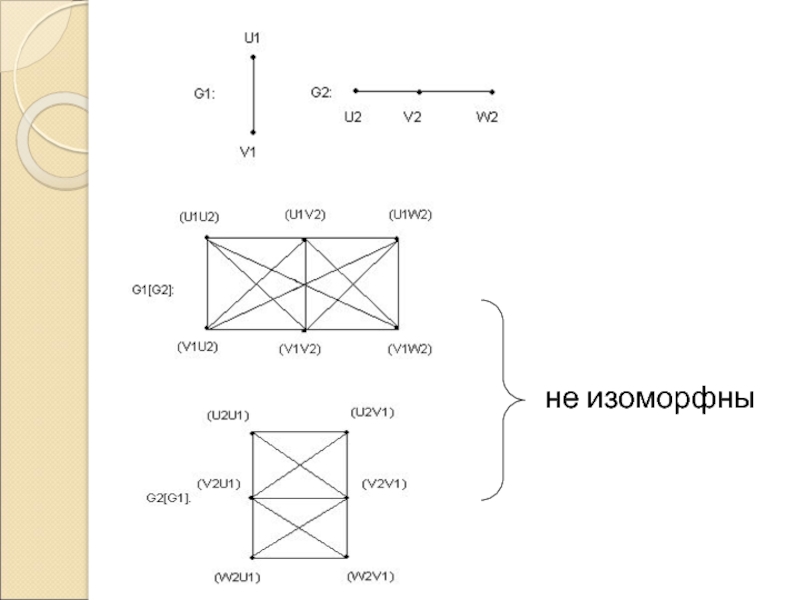
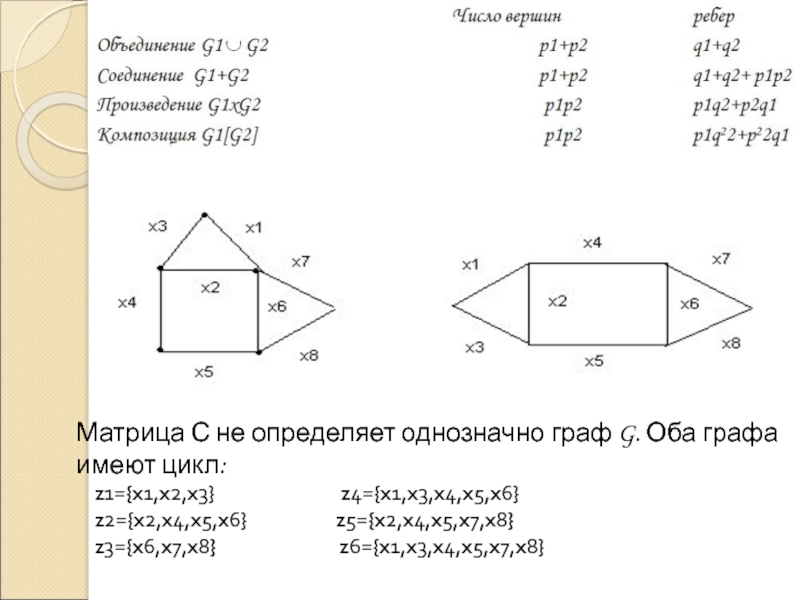

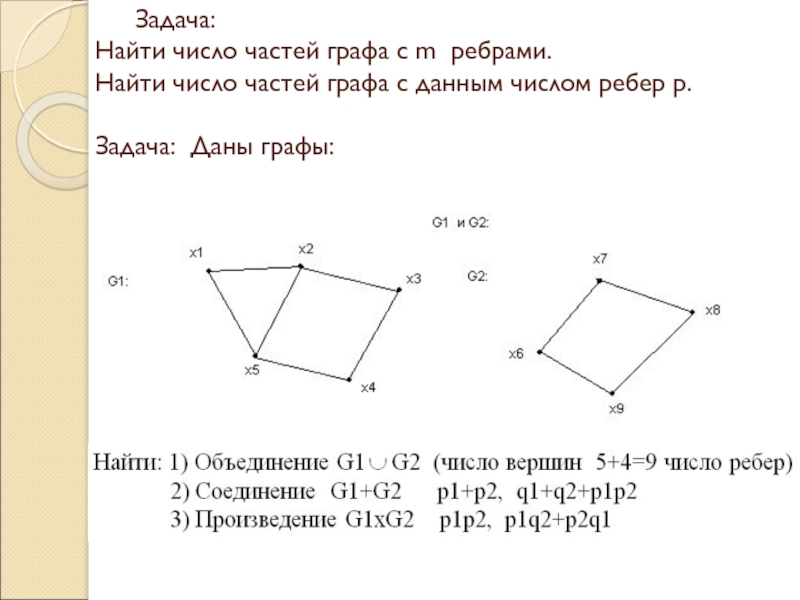
![Матрицы графов и их свойства 4) Композицию G1[G2] и G2[G1] 4) Композицию G1[G2] и G2[G1]](/img/thumbs/7931216ea103a23a206c73773addbe50-800x.jpg)