Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Механические колебания
Содержание
- 1. Механические колебания
- 2. Колебания физического маятникаФизический маятник - произвольное
- 3. Колебания физического маятника (1)Основной закон динамикивращательного движения
- 4. Колебания физического маятника (2)Проекцию углового ускорения можно
- 5. Колебания физического маятника (3)Уравнение аналогично дифференциальному уравнению
- 6. Колебания физического маятника (4)Подстановка функции и ее
- 7. Колебания физического маятника (5)Физический маятник совершает гармонические
- 8. Колебания математического маятникаМатематическим маятником называется точечное тело,
- 9. Колебания математического маятника (2)Так как математический маятник
- 10. Колебания математического маятника (3)Решением этого уравнения, как
- 11. Колебания математического маятника (4)Формула периода колебаний математического
- 12. Приведенная длина физического маятника Период колебаний математического
- 13. Приведенная длина физического маятника (2)Приведенной длиной физического
- 14. Электромагнитные колебанияНезатухающие колебания в колебательном контуре
- 15. Физические процессы в колебательном контуре1. Конденсатор заряжен.Возникает
- 16. Физические процессы в колебательном контуре3. Конденсатор разрядился.
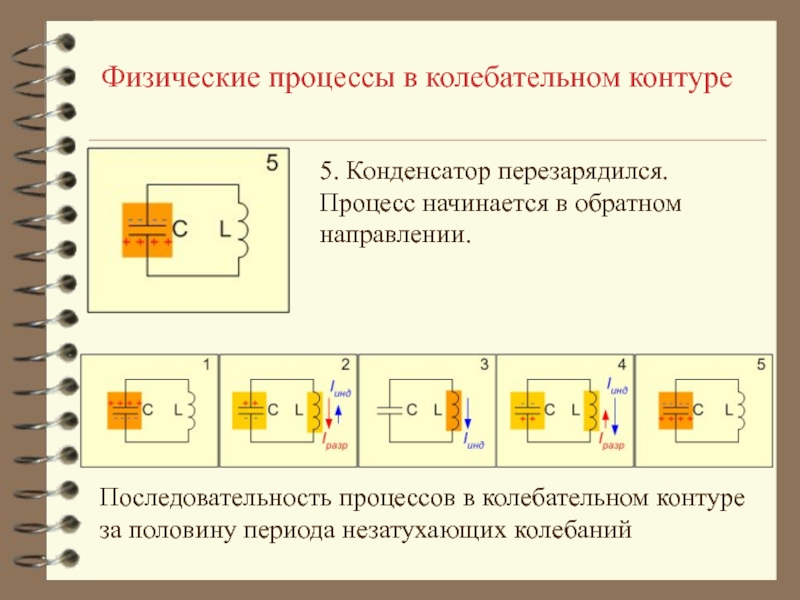
- 17. Физические процессы в колебательном контуре5. Конденсатор перезарядился.Процесс
- 18. Дифференциальное уравнение незатухающих колебаний в колебательном контуреКогда
- 19. Дифференциальное уравнение незатухающих колебаний в колебательном контуреНапряжение
- 20. Уравнение незатухающих электромагнитных колебанийДифференциальное уравнение можно переписать
- 21. Заряд конденсатора изменяется по гармоническому закону, q0
- 22. Формула Томсона.Циклическая частота всех этих гармонических колебаний
- 23. Формула Томсона.Период колебаний (формула Томсона).Джозеф Джон ТомсонУильям Томсон(лорд Кельвин)
- 24. Изменение тока и напряжения в процессе незатухающих
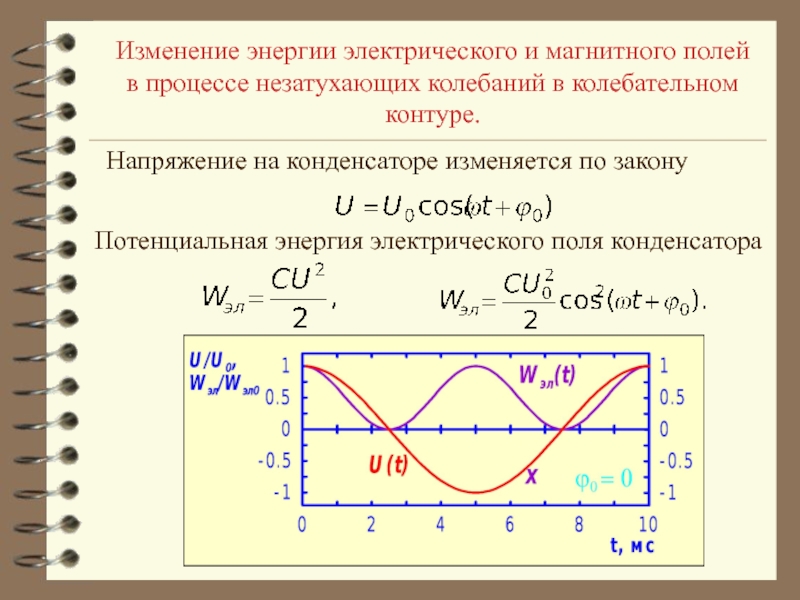
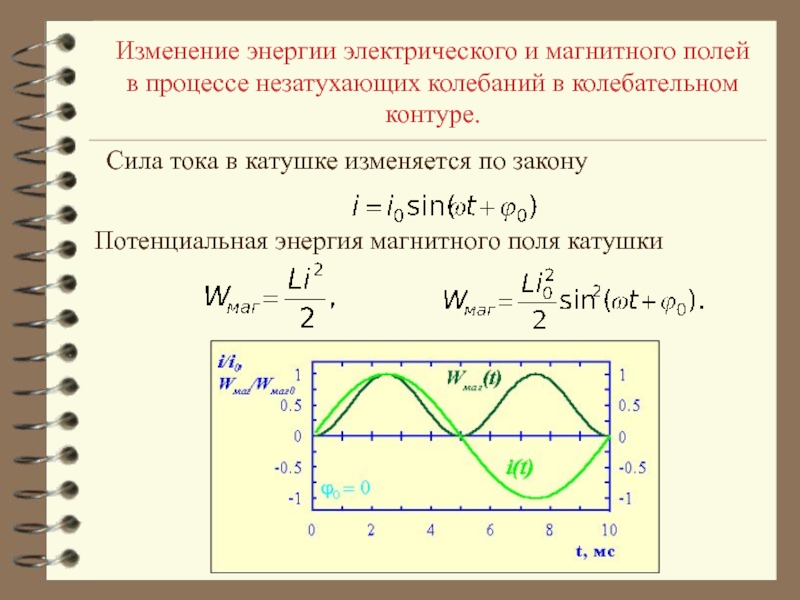
- 25. Изменение энергии электрического и магнитного полей в
- 26. Изменение энергии электрического и магнитного полей в
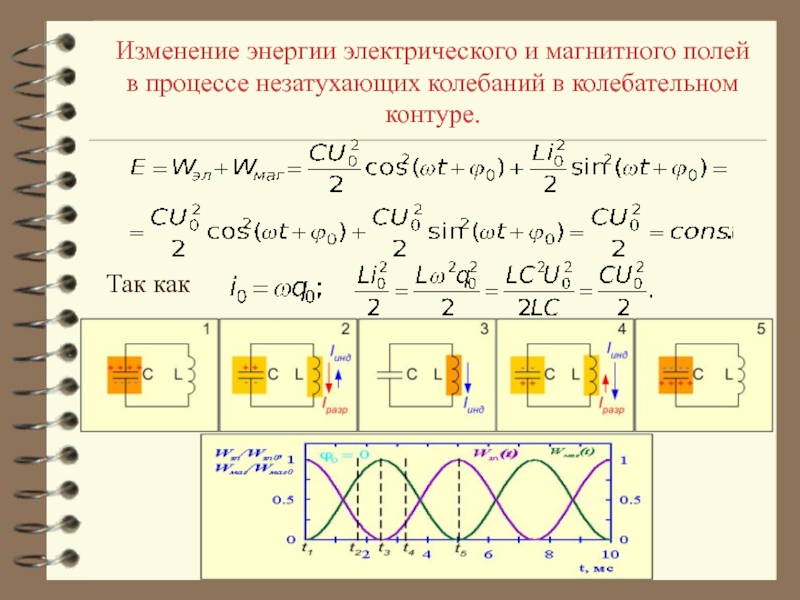
- 27. Изменение энергии электрического и магнитного полей в процессе незатухающих колебаний в колебательном контуре.Так как
- 28. Аналогия между механическими и электромагнитным колебаниями
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. Слайд 32
- 33. Скачать презентанцию
Слайды и текст этой презентации
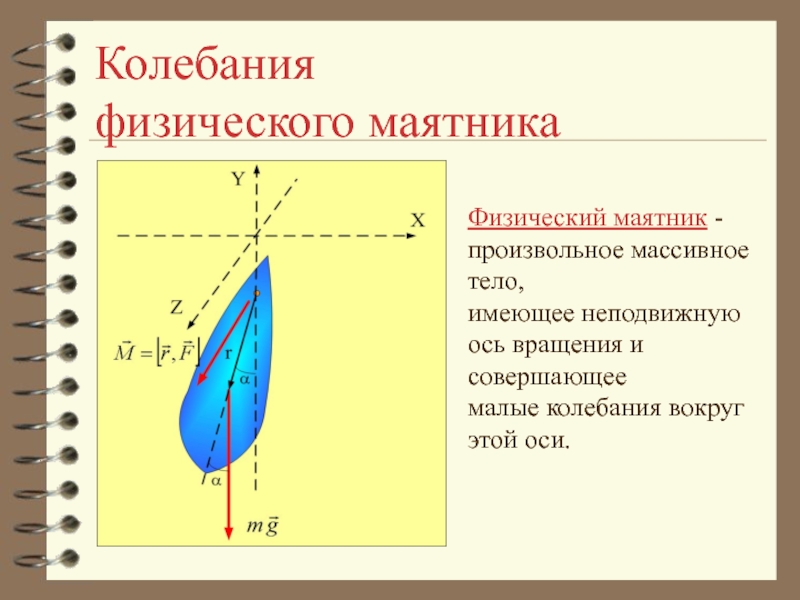
Слайд 2Колебания
физического маятника
Физический маятник - произвольное массивное тело,
имеющее неподвижную
ось вращения и совершающее
Слайд 3Колебания физического маятника (1)
Основной закон динамики
вращательного движения :
Момент силы тяжести
Проекция
момента силы тяжести на ось OZ:
Уравнение основного закона динамики
вращательного движения
в проекциях на OZ:Слайд 4Колебания
физического маятника (2)
Проекцию углового ускорения можно представить как
(векторы углового
перемещения и углового ускорения направлены в противоположные стороны)
Теперь уравнение движения
маятника принимает вид:При малых углах отклонения маятника a можно считать, что sina=a, поэтому
Слайд 5Колебания
физического маятника (3)
Уравнение аналогично дифференциальному
уравнению колебаний груза на
пружине,
следовательно, его решение можно записать в виде
Убедимся, что эта
функция является решением дифференциальногоуравнения, для чего найдем ее вторую производную:
Слайд 6Колебания
физического маятника (4)
Подстановка функции и ее второй производной в
дифференциальное уравнение дает:
Период гармонических колебаний физического маятника
Гармоническая функция является решением
дифференциального уравнения, еслиСлайд 7Колебания
физического маятника (5)
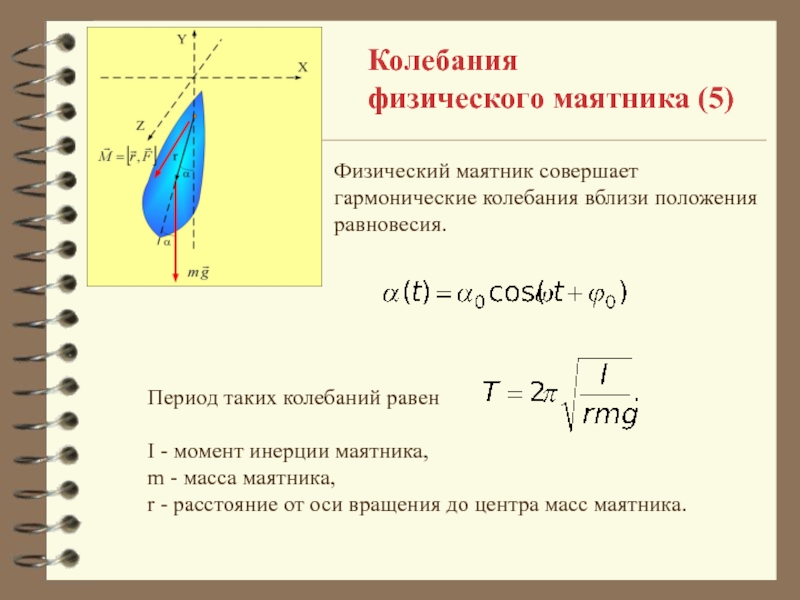
Физический маятник совершает гармонические колебания вблизи положения
равновесия.
Период таких колебаний равен
I - момент инерции маятника,
m
- масса маятника,r - расстояние от оси вращения до центра масс маятника.
Слайд 8Колебания математического маятника
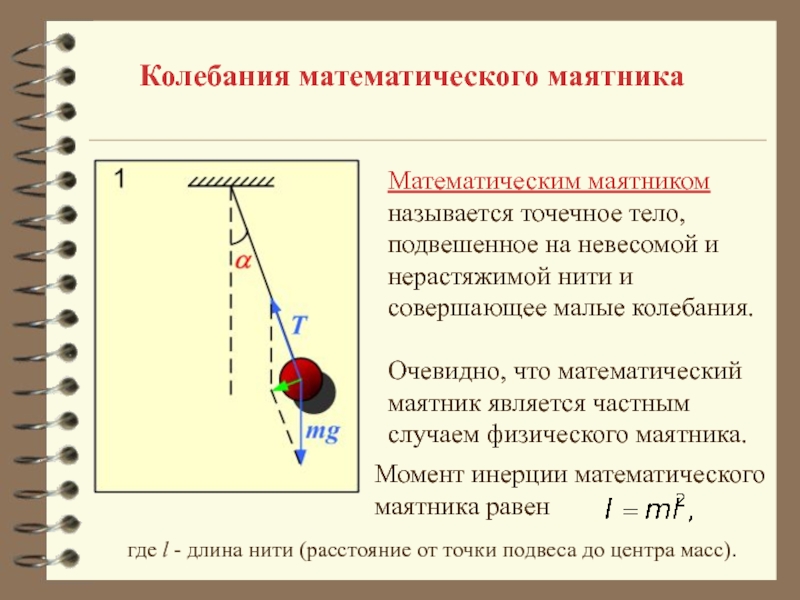
Математическим маятником
называется точечное тело,
подвешенное на невесомой
и
нерастяжимой нити и
совершающее малые колебания.
Очевидно, что математический
маятник является
частнымслучаем физического маятника.
Момент инерции математического маятника равен
где l - длина нити (расстояние от точки подвеса до центра масс).
Слайд 9Колебания
математического маятника (2)
Так как математический маятник есть частный случай
физического, воспользуемся дифференциальным
уравнением колебаний физического маятника:
Момент инерции математического маятника
равенследовательно,
Дифференциальное уравнение колебаний принимает вид:
Слайд 10Колебания
математического маятника (3)
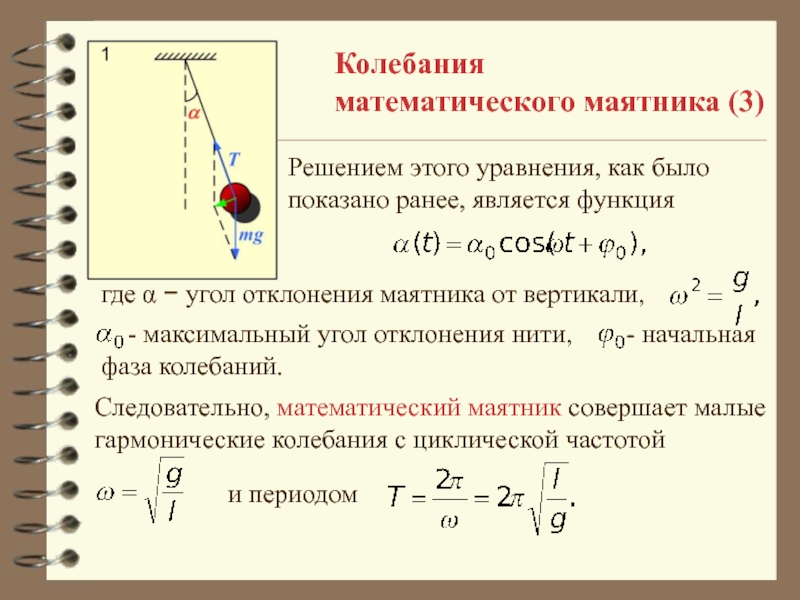
Решением этого уравнения, как было показано ранее,
является функция
- максимальный угол отклонения нити,
- начальнаяфаза колебаний.
Следовательно, математический маятник совершает малые гармонические колебания с циклической частотой
где a - угол отклонения маятника от вертикали,
и периодом
Слайд 11Колебания
математического маятника (4)
Формула периода колебаний математического маятника
впервые была
получена Х. Гюйгенсом и носит его имя.
Гюйгенс Христиан (1629 –
1695), нидерландский ученый. Изобрел (1657) маятниковые часы, установил законы колебаний математического и физического маятников.Создал (1678, опубликовал 1690) волновую теорию света, Совместно с Р. Гуком установил постоянные (реперные) точки термометра. Усовершенствовал телескоп. Открыл кольцо у Сатурна и его спутник Титан. Автор одного из первых трудов по теории вероятностей (1657).Слайд 12Приведенная длина физического маятника
Период колебаний математического маятника определяется по
формуле
Если длина математического маятника
Период колебаний физического маятника равен
Пусть
, тогдаоткуда
то периоды математического и физического маятников совпадают.
Слайд 13Приведенная длина физического маятника (2)
Приведенной длиной физического маятника называется длина
такого математического маятника, у которого период колебаний равен периоду колебаний
данного физического маятника.I - момент инерции физического маятника относительно
его оси вращения, m - масса физического маятника,
r - расстояние от оси вращения до центра масс физического
маятника.
Слайд 15Физические процессы в колебательном контуре
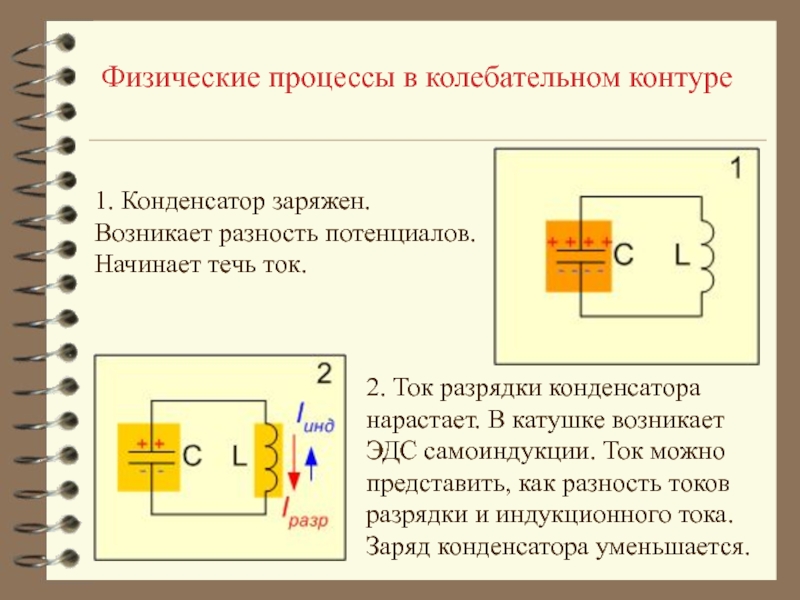
1. Конденсатор заряжен.
Возникает разность потенциалов.
Начинает течь
ток.
2. Ток разрядки конденсатора
нарастает. В катушке возникает
ЭДС самоиндукции.
Ток можнопредставить, как разность токов
разрядки и индукционного тока.
Заряд конденсатора уменьшается.
Слайд 16Физические процессы в колебательном контуре
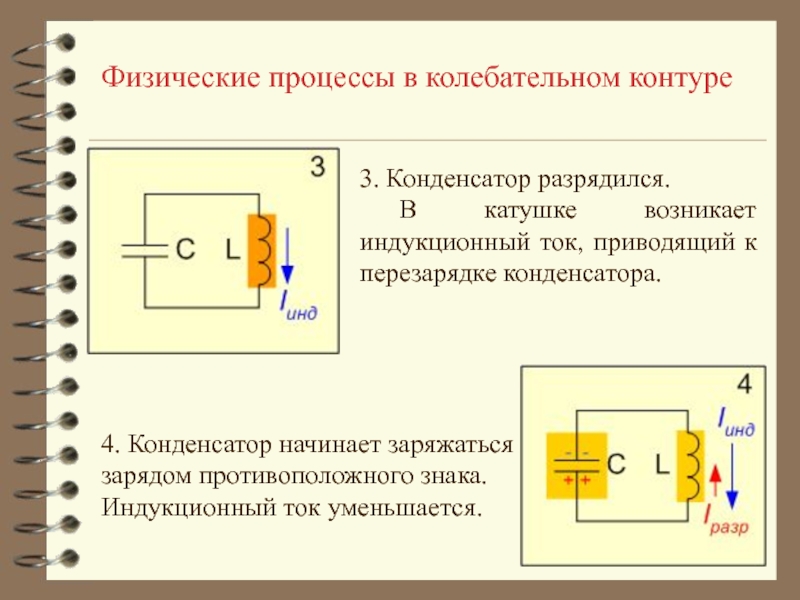
3. Конденсатор разрядился.
В катушке возникает
индукционный ток, приводящий к перезарядке конденсатора.
4. Конденсатор начинает заряжаться
зарядом противоположного
знака.Индукционный ток уменьшается.