Метод искусственного базиса Цель метода искусственного базиса – построение

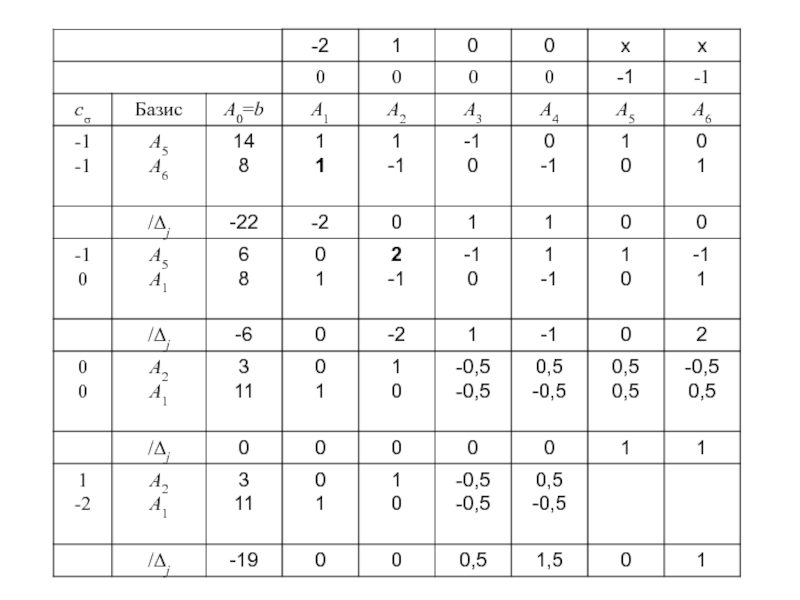
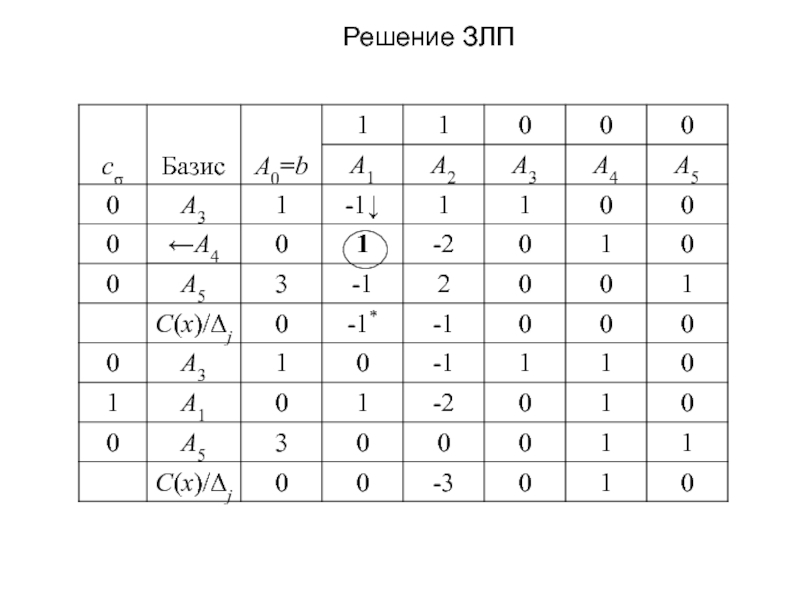
БДП (либо установить отсутствие БДП).
ЗЛП задана в канонической форме,

(

Этого всегда можно добиться, умножив уравнения на -1):

(1)

ЗЛП (1.) и искусственных переменных, введенных в ЗЛП (2):

для поиска начального БДП.
Единичные векторы An+1, An+2, …, An+m

образуют искусственный базис системы ограничений ЗЛП (2). Они представляют собой единичную матрицу размера m  m.
В ЗЛП (2) мы имеем начальный БДП, в котором первые n координат равны нулю.
Пусть множество допустимых планов задачи (1) - D1, а множество допустимых планов задачи (2) - D2.

Пусть

оптимальный план ЗЛП (2), тогда:
Если , то план является планом задачи (1), т.е. D1.
Если , то ЗЛП (1) не имеет допустимых планов, т.е. D1 есть пустое множество (D1 = ).
Замечание. Вспомогательная задача (2) всегда имеет оптимальный план.

к каноническому виду:

вспомогательную задачу, предварительно введя две искусственные переменные х5  0

и х6  0.

и значение целевой функции на этом плане:


Оптимальный план вспомогательной задачи

есть начальный БДП основной задачи. После чего необходимо приступить к ее решению также симплекс-методом. Оптимальный план основной задачи:
х* = (11; 3; 0; 0); С1(х*) = – 19; С(х*) = 19

(х10, х20,…, хn0) - БДП задачи (1)
Ax0 = b

эквивалентно

(1)

 - носитель плана, следовательно - ,
или в матричной форме записи:

(2)

часть исходного вектора х0 , из которого удалены нулевые (свободные)

компоненты. Для плана х0 можно построить симплекс-таблицу, причем предположим, что среди двойственных оценок имеются отрицательные , т.е. план не оптимальный.

  и все элементы k-го вектор-столбца меньше или равны

нулю, т.е. , i, то ЗЛП неразрешима. Другими словами, в данной ситуации целевая функция не ограничена на допустимом множестве, т. е. С(х)   .

х0 = (0; 0; 1; 0; 3).

базис вектор А2, однако координаты этого вектора . На основании

только что доказанной теоремы можно сделать заключение, что данная ЗЛП неразрешима, она не имеет оптимальных планов, а ее целевая функция С(х) → +∞ на множестве допустимых планов.