Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод проекции градиента
Содержание
- 1. Метод проекции градиента
- 2. Метод проекции градиента является обобщением метода наискорейшего
- 3. 1. Стартовую точку выбираем произвольноЛинии равного уровня
- 4. Рассмотрим, какие изменения нужно внести в метод
- 5. Найдем направление антиградиента. Перемещение по этому направлению
- 6. Возможные варианты окончания поиска минимума методом проекции
- 7. Скачать презентанцию
Метод проекции градиента является обобщением метода наискорейшего спуска на случай, когда решается задача минимизации нелинейной функции с ограничениями.Хотя метод применим и в задачах с нелинейными ограничениями, хорошая сходимость имеет место только
Слайды и текст этой презентации
Слайд 1Метод проекции градиента
(минимизация выпуклого критерия на линейной системе ограничений –
равенств и неравенств)
Слайд 2Метод проекции градиента является обобщением метода наискорейшего спуска на случай,
когда решается задача минимизации нелинейной функции с ограничениями.
Хотя метод применим
и в задачах с нелинейными ограничениями, хорошая сходимость имеет место только в случае, когда ограничения – линейны.Постановка задачи: найти x (n-мерный вектор) , доставляющий минимум выпуклой скалярной функции f(x) при условиях: A1x = B1, A2x ≤ B2
Примечание: Если должна быть учтена неотрицательность х, то, в отличие от ЛП, ограничения х≥0 должны быть включены в общую систему ограничений в форме -х ≤ 0.
Напомним основные позиции метода наискорейшего спуска (поиск минимума выпуклой функции f(x) без ограничений)
Слайд 3
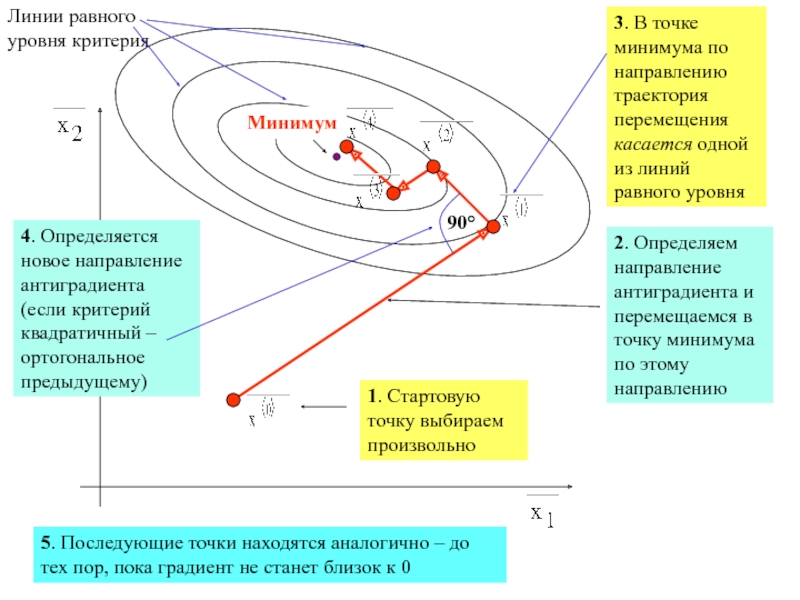
1. Стартовую точку выбираем произвольно
Линии равного уровня критерия
Минимум
90°
2. Определяем направление
антиградиента и перемещаемся в точку минимума по этому направлению
3. В
точке минимума по направлению траектория перемещения касается одной из линий равного уровня4. Определяется новое направление антиградиента (если критерий квадратичный – ортогональное предыдущему)
5. Последующие точки находятся аналогично – до тех пор, пока градиент не станет близок к 0
Слайд 4
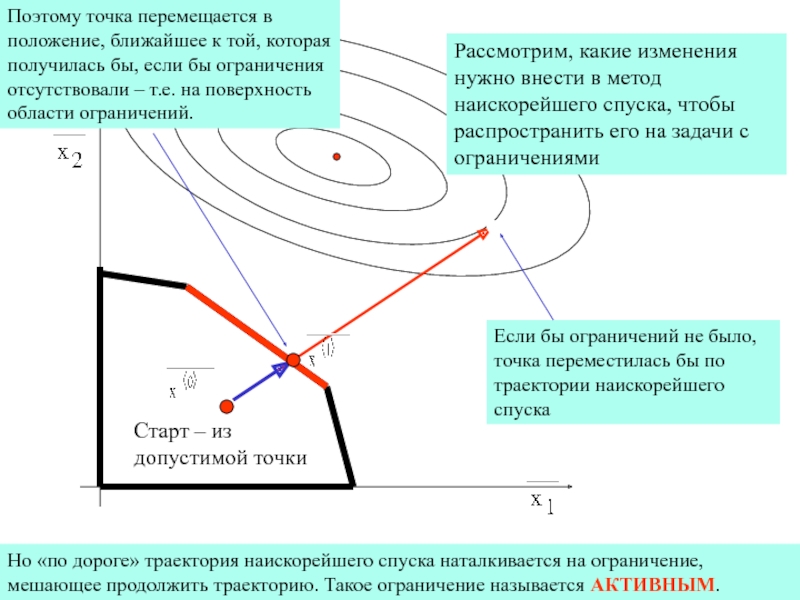
Рассмотрим, какие изменения нужно внести в метод наискорейшего спуска, чтобы
распространить его на задачи с ограничениями
Старт – из допустимой точки
Если
бы ограничений не было, точка переместилась бы по траектории наискорейшего спускаНо «по дороге» траектория наискорейшего спуска наталкивается на ограничение, мешающее продолжить траекторию. Такое ограничение называется АКТИВНЫМ.
Поэтому точка перемещается в положение, ближайшее к той, которая получилась бы, если бы ограничения отсутствовали – т.е. на поверхность области ограничений.
Слайд 5
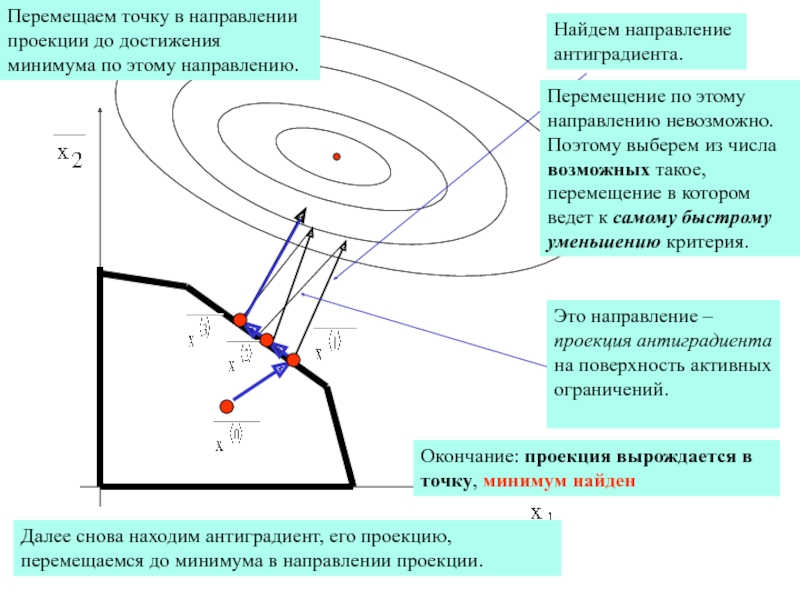
Найдем направление антиградиента.
Перемещение по этому направлению невозможно. Поэтому выберем
из числа возможных такое, перемещение в котором ведет к самому
быстрому уменьшению критерия.Это направление – проекция антиградиента на поверхность активных ограничений.
Перемещаем точку в направлении проекции до достижения минимума по этому направлению.
Далее снова находим антиградиент, его проекцию, перемещаемся до минимума в направлении проекции.
Окончание: проекция вырождается в точку, минимум найден
Слайд 6
Возможные варианты окончания поиска минимума методом проекции градиента:
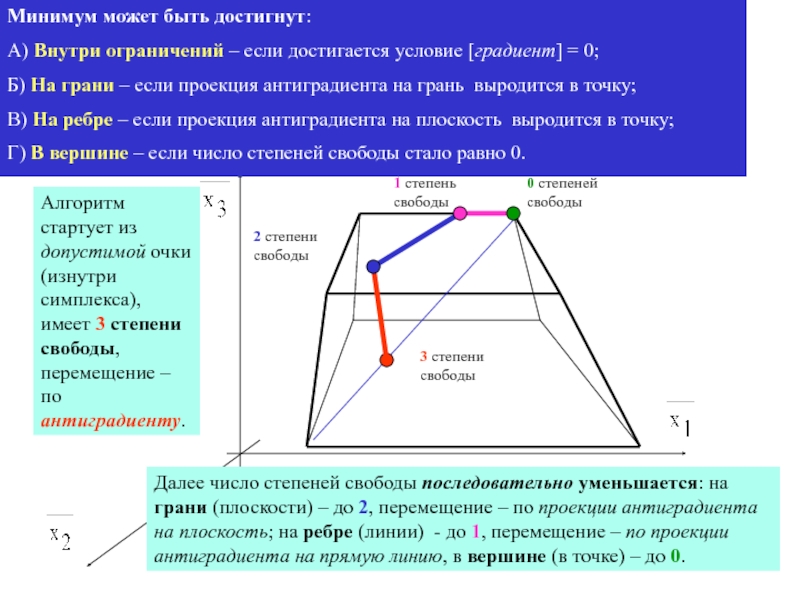
Рассмотрим задачу поиска
минимума функции f(x) 3-мерного вектора х.
Пусть область ограничений –
линейная (в форме призмы, трехмерный симплекс)3 степени свободы
2 степени свободы
1 степень свободы
0 степеней свободы
Алгоритм стартует из допустимой очки (изнутри симплекса), имеет 3 степени свободы, перемещение – по антиградиенту.
Далее число степеней свободы последовательно уменьшается: на грани (плоскости) – до 2, перемещение – по проекции антиградиента на плоскость; на ребре (линии) - до 1, перемещение – по проекции антиградиента на прямую линию, в вершине (в точке) – до 0.
Минимум может быть достигнут:
А) Внутри ограничений – если достигается условие [градиент] = 0;
Б) На грани – если проекция антиградиента на грань выродится в точку;
В) На ребре – если проекция антиградиента на плоскость выродится в точку;
Г) В вершине – если число степеней свободы стало равно 0.
