Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методическая разработка Савченко Е.М. МОУ гимназия №1, г. Полярные Зори,
Содержание
- 1. Методическая разработка Савченко Е.М. МОУ гимназия №1, г. Полярные Зори,
- 2. Рассмотрим фигуру, составленную из отрезков так, что
- 3. Многоугольник с n вершинами называется n-угольникомn=3n=4n=5n=6n=7n=8n=9
- 4. Любой многоугольник разделяет плоскость на две части,АВСDEFGHодна
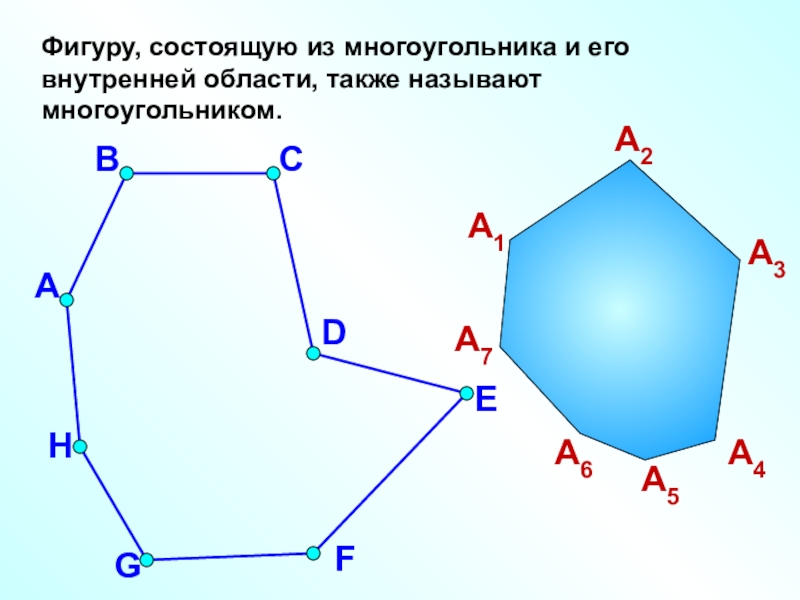
- 5. Фигуру, состоящую из многоугольника и его внутренней области, также называют многоугольником.АВСDEFGHА1А2А3А4А5А6А7
- 6. Примеры многоугольников
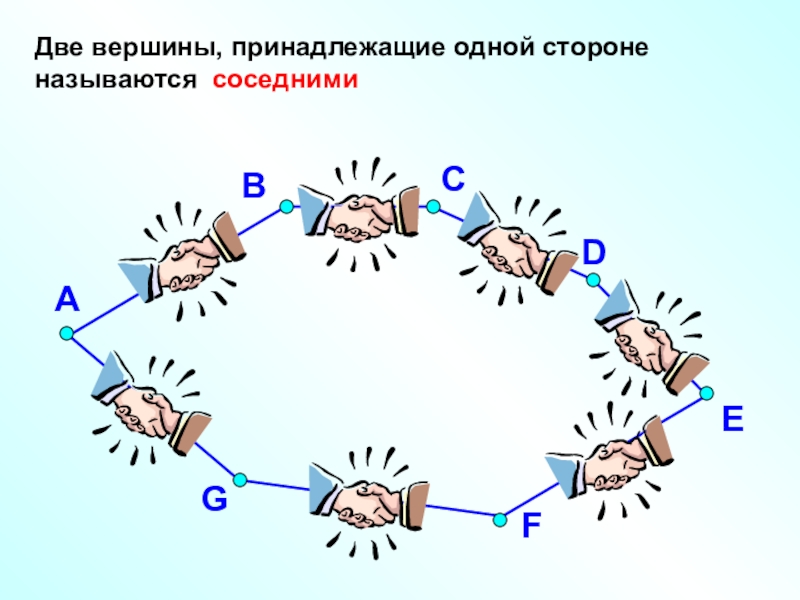
- 7. АВDEFGДве вершины, принадлежащие одной стороне называются соседнимиС
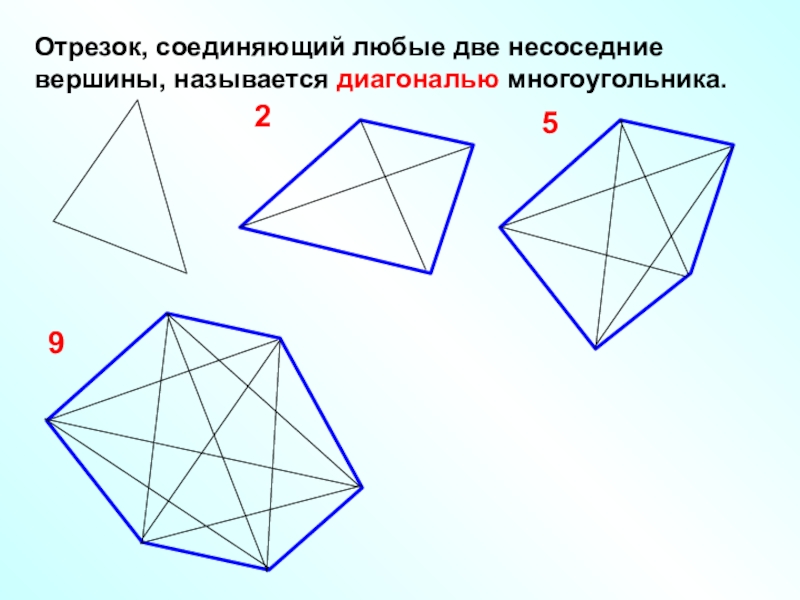
- 8. Отрезок, соединяющий любые две несоседние вершины, называется диагональю многоугольника.259
- 9. САВDEFGОтрезок, соединяющий любые две несоседние вершины, называется диагональю многоугольника.14
- 10. Многоугольник называется выпуклым, если он лежит по
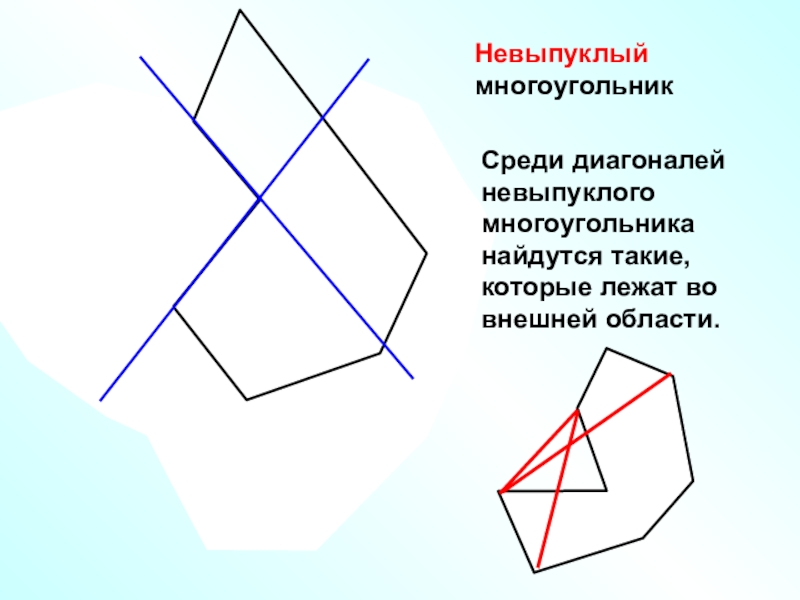
- 11. Невыпуклый многоугольникСреди диагоналей невыпуклого многоугольника найдутся такие, которые лежат во внешней области.
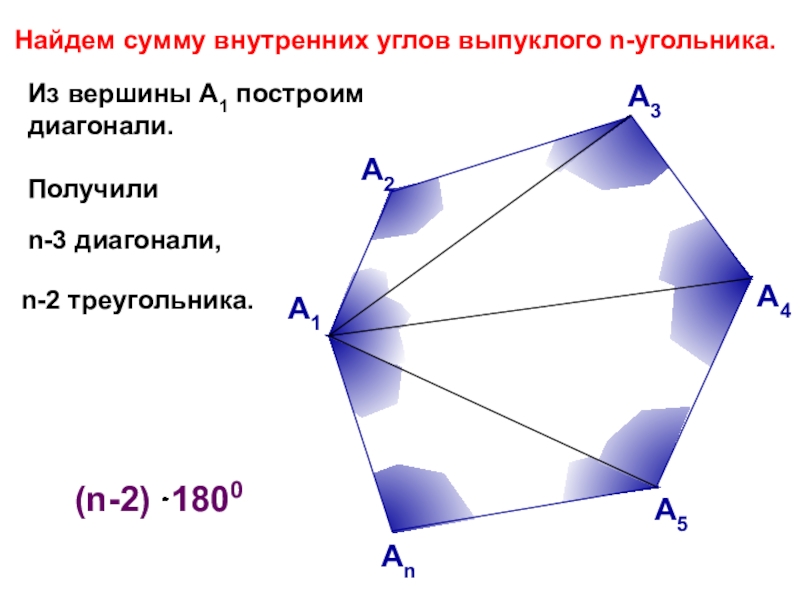
- 12. Из вершины А1 построим диагонали.Получили А1Найдем сумму внутренних углов выпуклого n-угольника.А2А3А4А5Аnn-2 треугольника.n-3 диагонали,
- 13. Скачать презентанцию
Рассмотрим фигуру, составленную из отрезков так, что смежные отрезки не лежат на одной прямой, а несмежные отрезки не имеют общих точек. АВСDEFGHТакая фигура называется многоугольником.Точки А, В, С,…, H –
Слайды и текст этой презентации
Слайд 2Рассмотрим фигуру, составленную из отрезков так, что смежные отрезки не
лежат на одной прямой, а несмежные отрезки не имеют общих
точек.А
В
С
D
E
F
G
H
Такая фигура называется многоугольником.
Точки А, В, С,…, H – вершины многоугольника.
Отрезки АВ, ВС,…, HА – стороны многоугольника.
Сумма длин всех сторон – периметр многоугольника.
Слайд 4Любой многоугольник разделяет плоскость на две части,
А
В
С
D
E
F
G
H
одна часть называется внутренней
областью,
другая часть называется внешней областью внешней областью
Слайд 5Фигуру, состоящую из многоугольника и его внутренней области, также называют
многоугольником.
А
В
С
D
E
F
G
H
А1
А2
А3
А4
А5
А6
А7
Слайд 9С
А
В
D
E
F
G
Отрезок, соединяющий любые две несоседние вершины, называется диагональю многоугольника.
14
Слайд 10Многоугольник называется выпуклым, если он лежит по одну сторону от
каждой прямой, проходящей через две его соседние вершины.
Диагонали выпуклого
многоугольника лежат во внутренней области фигуры.
Слайд 11Невыпуклый
многоугольник
Среди диагоналей невыпуклого многоугольника найдутся такие, которые лежат во
внешней области.
Слайд 12Из вершины А1 построим диагонали.
Получили
А1
Найдем сумму внутренних углов выпуклого
n-угольника.
А2
А3
А4
А5
Аn
n-2 треугольника.
n-3 диагонали,
