Слайд 108/13/2019
Тема 2 Методы оптимизации нулевого порядка
Описание общего алгоритма методов покоординатного
спуска
Особенности программной реализации
Метод ГАУССА-ЗЕЙДЕЛЯ
Метод ПАУЭЛЛА
Метод РОЗЕНБРОКА
Методы спуска с перебором направлений
Хука-Дживса и Нелдера-Мидта
Слайд 208/13/2019
Методы покоординатного спуска
Среди методов нулевого порядка можно выделить группу методов
покоординатного спуска:
Гаусса-Зейделя,
Пауэлла,
Дэвиса-Свена-Кемпи (ДСК),
Розенброка.
Алгоритм этих методов в общем
одинаков и описывается следующим образом:
Слайд 308/13/2019
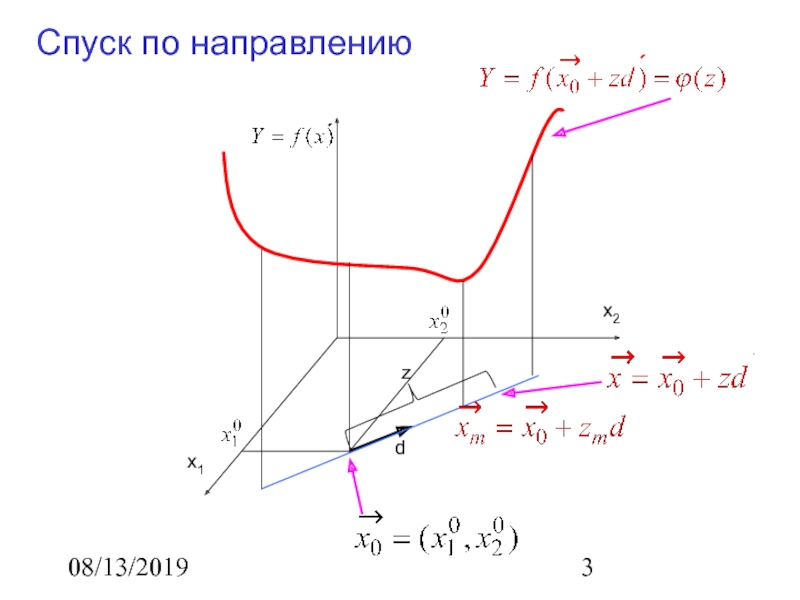
x1
x2
d
z
Спуск по направлению
Слайд 408/13/2019
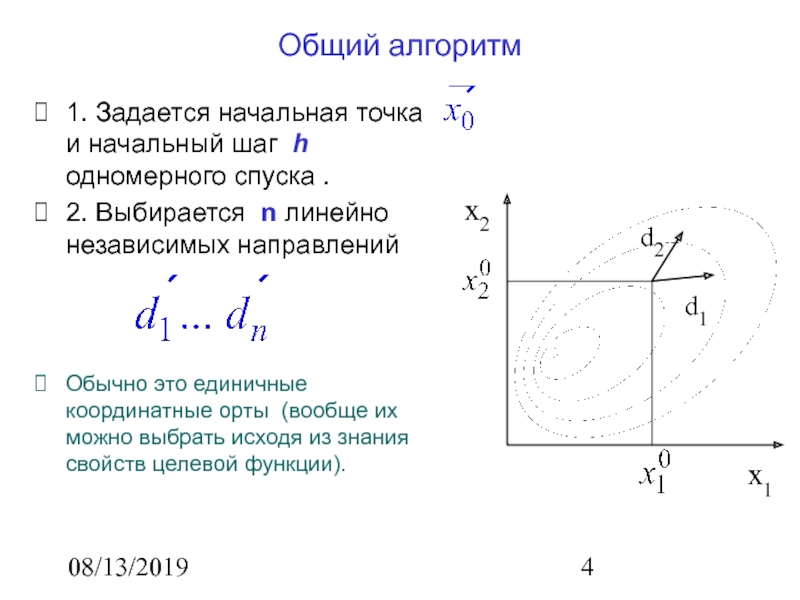
Общий алгоритм
1. Задается начальная точка и
начальный шаг h одномерного спуска .
2. Выбирается n линейно независимых
направлений
Обычно это единичные координатные орты (вообще их можно выбрать исходя из знания свойств целевой функции).
x1
x2
d1
d2
Слайд 508/13/2019
Общий алгоритм
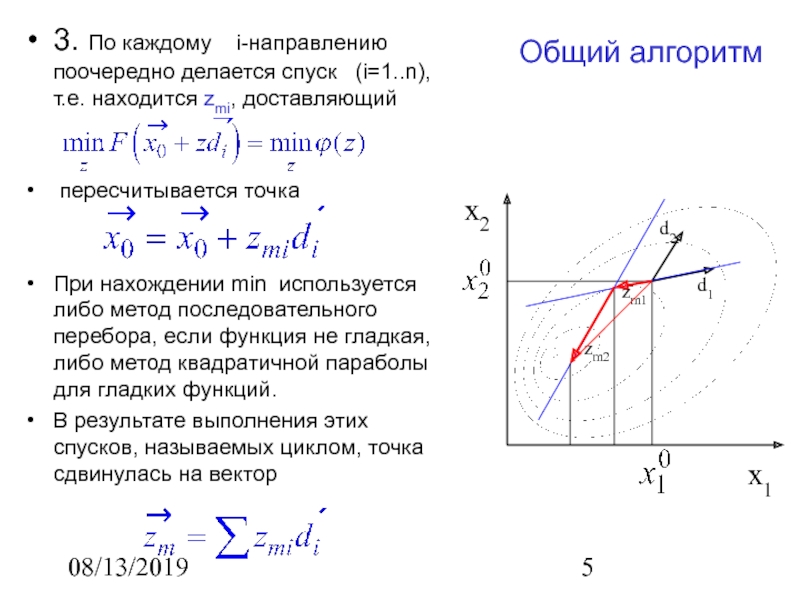
3. По каждому i-направлению поочередно делается спуск
(i=1..n), т.е. находится zmi, доставляющий
пересчитывается точка
При нахождении
min используется либо метод последовательного перебора, если функция не гладкая, либо метод квадратичной параболы для гладких функций.
В результате выполнения этих спусков, называемых циклом, точка сдвинулась на вектор
x1
x2
d1
d2
zm1
zm2
Слайд 608/13/2019
Общий алгоритм
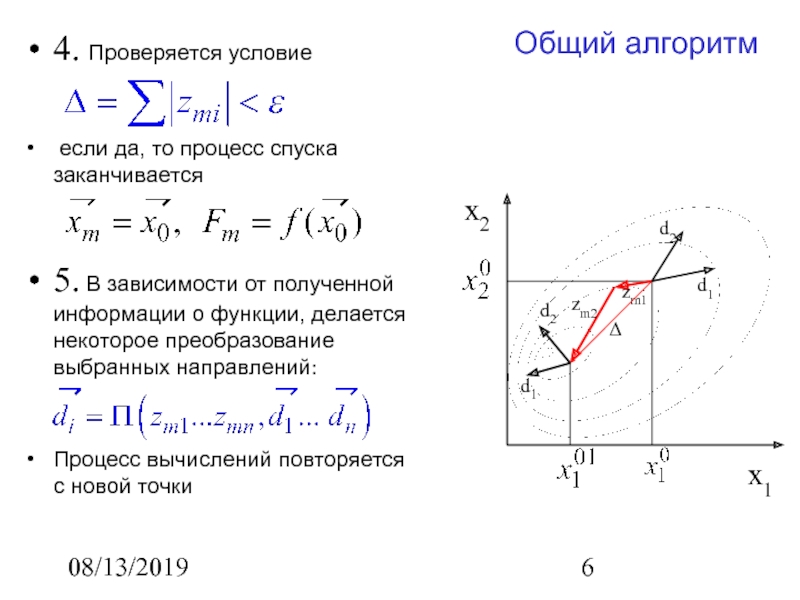
4. Проверяется условие
если да, то процесс спуска заканчивается
5.
В зависимости от полученной информации о функции, делается некоторое преобразование
выбранных направлений:
Процесс вычислений повторяется с новой точки
x1
x2
d1
d2
zm1
zm2
Δ
d1
d2
Слайд 708/13/2019
Особенности программной реализации.
При программной реализации следует описать отдельно подпрограмму
вычисления минимизируемой функции, например, для целевой функции, имеющей вид
const n=2;
type
mas=array[l..n] of real;
function F(х:mas): real;
begin
F:=sqr(x[1]+2*x[2])
end;
Слайд 808/13/2019
Особенности программной реализации
После этого напишем подпрограмму метода оптимизации:
Type fun=function (x:mas):real
Procedure
MPSP(F:fun;
var x0:mas;eps,h:real;var fm:real);
внутри которой следует ввести:
для координат векторов
направлений массив D[i,k] где помещается i-я координата вектора dk
var
D:array[1..n,1..n] of real
zm,x,a,b:array[1..n] of real;
рабочие массивы zm, x,
a и b в методе Розенброка, ДСК, Пауэлла;
Слайд 908/13/2019
Подпрограмма для функции ϕ(z)
вдоль направления
function F1(z:
real): real;
begin
for k:=1 to n do
x[k]=x0[k]+z*D[i,k];
F1:=F(x);
end;
Слайд 1008/13/2019
Подпрограмма метода одномерного поиска
Function MPP(z0,h,eps:real):real;
begin
y1:=F1(z0); z1:=z0;
repeat
repeat
z0:=z1; y0:=y1;
z1:=z0+h; y1:=F1(z1);
until y1>y0;
h:=-h/4;
until abs(h) Result:=y0;
end;
Слайд 1108/13/2019
Подпрограмма преобразования векторов направлений [вычисляет d=∏(d,zm)]
Procedure PREOBD; (без параметров)
begin
.
. . . .
D[i.k]=........
end;
Отличаются методы видом оператора преобразования ∏ направлений
после каждого цикла спуска
Слайд 1208/13/2019
Реализация алгоритма спуска к минимуму
Begin
D:=0; for i:=1 to n
do D[i,i]:=1;
repeat
dl=0;
for i:=1 to n do //спуск по направлениям
begin
zm[i]:=MPP(0,h,h/5);
x0:=x;
dl:=dl+abs(zm[i]); //погрешность
end;
PREOBD; h:=h*0.5;
Until dlfm:=F(x0);
End;
Слайд 1308/13/2019
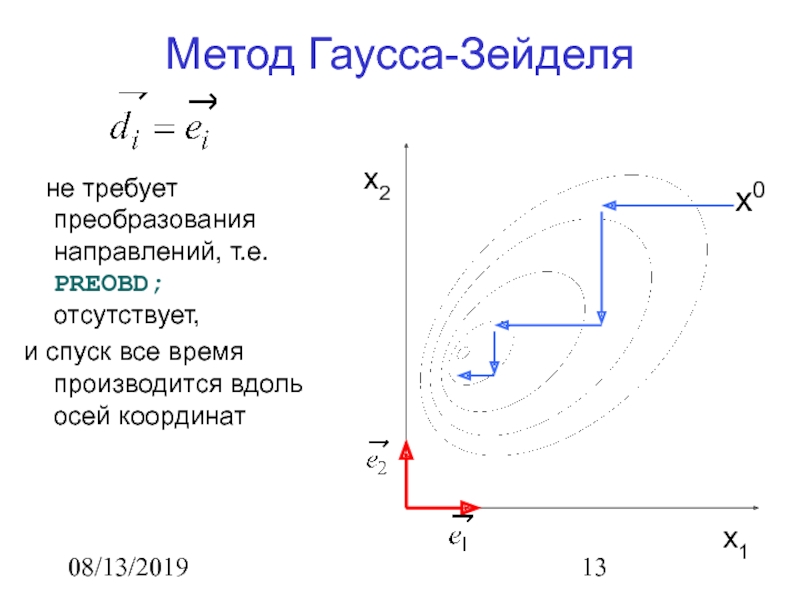
Метод Гаусса-Зейделя
не требует преобразования направлений, т.е. PREOBD; отсутствует,
и спуск все время производится вдоль осей координат
x1
x2
x0
Слайд 1408/13/2019
x1
x2
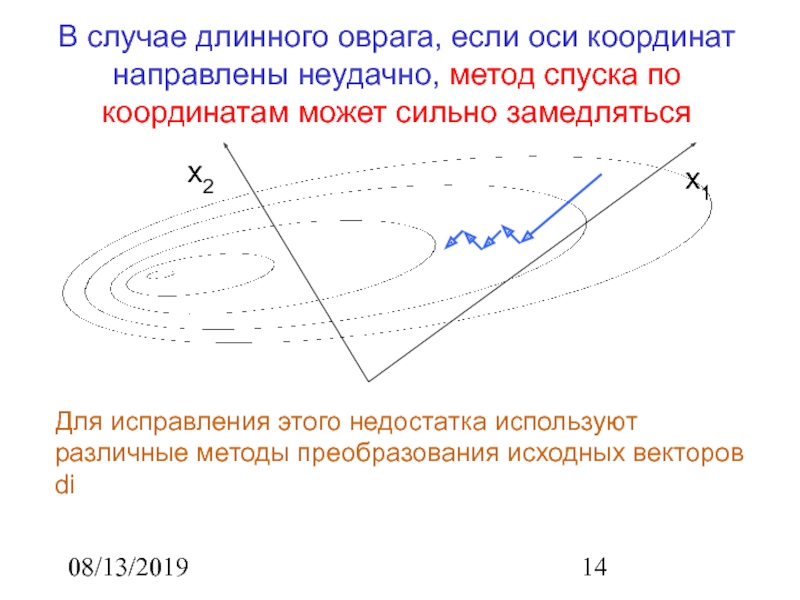
В случае длинного оврага, если оси координат направлены неудачно, метод
спуска по координатам может сильно замедляться
Для исправления этого недостатка используют
различные методы преобразования исходных векторов di
Слайд 1508/13/2019
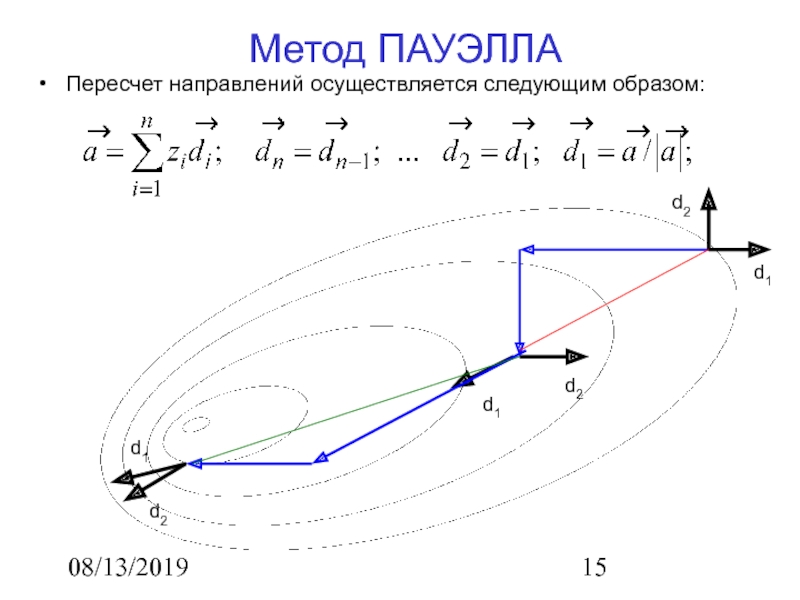
Метод ПАУЭЛЛА
Пересчет направлений осуществляется следующим образом:
d1
d2
d2
d1
d2
d1
Слайд 1608/13/2019
Преобразование векторов di
Procedure PREOBD;
Var a:MAS;
begin
for k=l to n do
begin a[k]=0;
for i=1 to n do
a[k]=a[k]+zm[i]*D[i,k]
end;
for i: =n downto 2 do
for k=1 to n do D[i,k]=D[i-1,k];
da=0; for k=l to n do
da=da+sqr(a[k]); da=sqrt(da);
for k=1 to n do D[1,k]=a[k]/da;
end;
Слайд 1708/13/2019
Метод Розенброка
Формулы пересчета направлений:
Ортогонализация направлений
Слайд 1808/13/2019
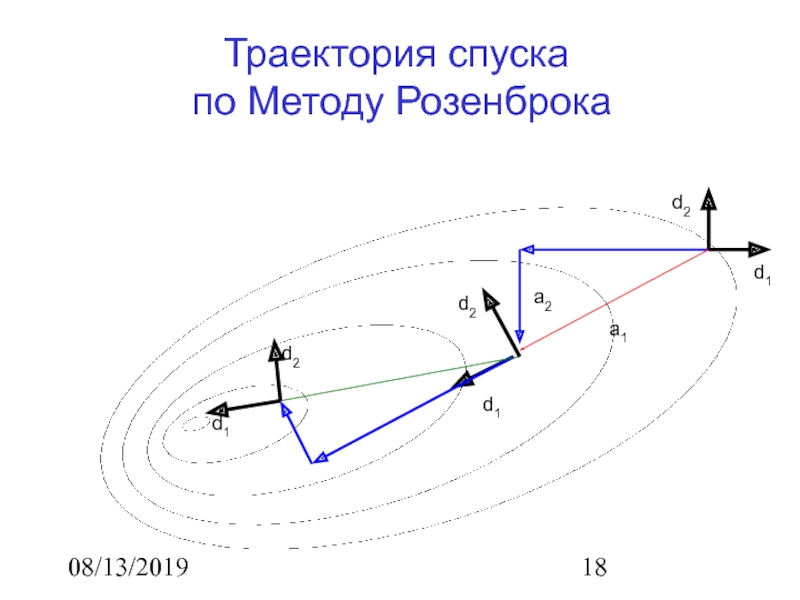
Траектория спуска
по Методу Розенброка
d1
d2
d2
d1
d2
d1
a1
a2
Слайд 1908/13/2019
Procedure PREOBD;//метод Розенброка
VAR a:array[1..n,l..n] of real;
c: array[l...,n] of real;
aa, cc,ad:real;
i,j,k,l: integer;
begin
for i=l to n do
for k=l to n do
begin a[i,k]=0; for j:=i to n do
a[i,k]=a[i,k]+zm[j]*D[j,k]
end;
da=0; for k=l to n do da=aa+sqr(a[1,k]); da=sqrt(da);
for k=1 to n do D[1,k]=a[1,k]/da;
for i=2 to n do
begin for k=l to n do
begin c[k]=a[i,k];
for j=1 to i-1 do
begin ad=0 for l=1 to n do ad=ad+а[i,1]*D[j,1]
c[k]=c[k]-ad*D[j,k];
end;
end;
dс=0; for k=l to n do dc=dc+sqr(c[k]); dc=sqrt(dc);
for k=l to n do d[i,k]=c[k]/dc;
end
end;
Слайд 2008/13/2019
Методы спуска с перебором направлений
Другая группа методов, нулевого порядка,
представителями которых являются методы
Последовательного покоординатного перебора
Хука-Дживса
Нелдера-Мида
иллюстрируют широкие возможности для творческого поиска разнообразных способов выбора направлений
Слайд 2108/13/2019
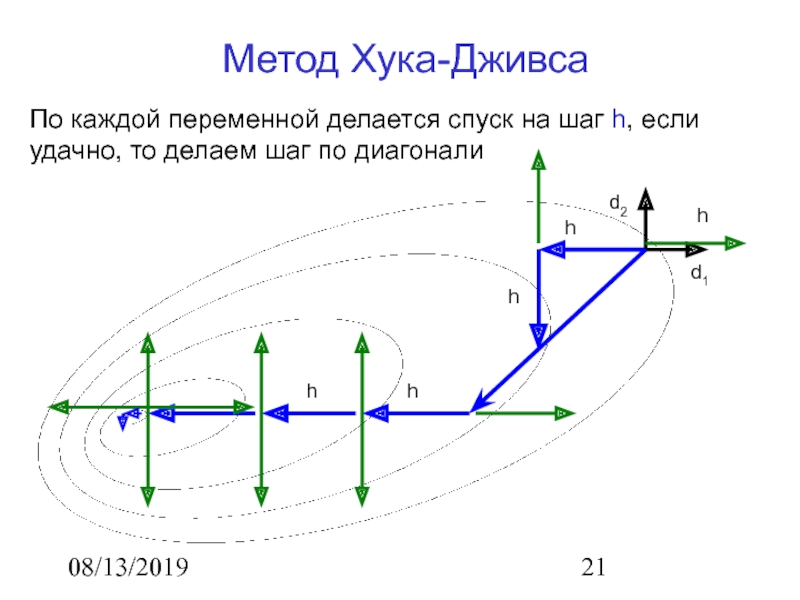
Метод Хука-Дживса
d1
d2
По каждой переменной делается спуск на шаг h,
если удачно, то делаем шаг по диагонали
h
h
h
h
h
Слайд 2208/13/2019
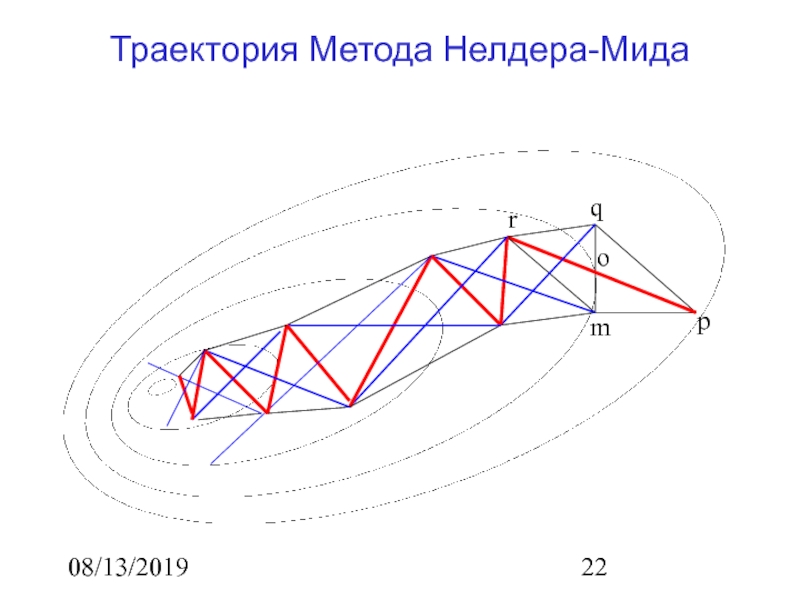
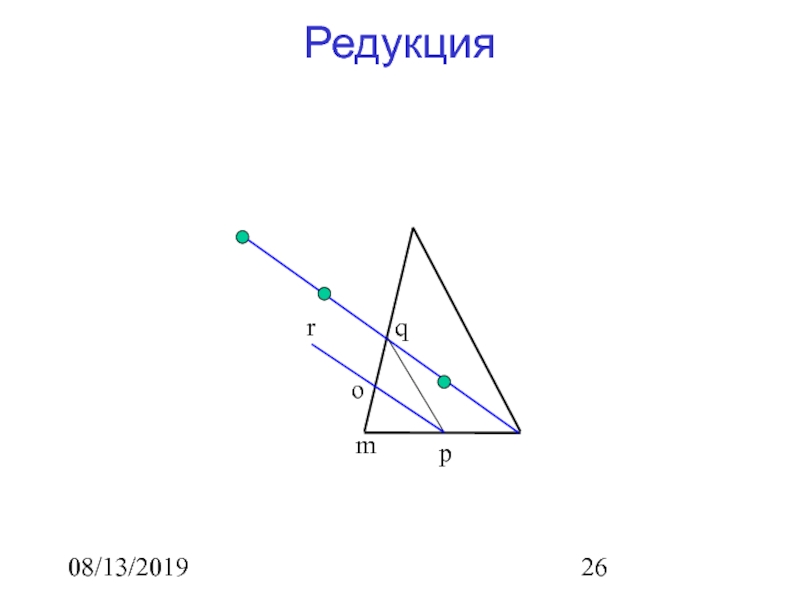
Траектория Метода Нелдера-Мида
p
m
q
o
r




![Методы нулевого порядка 08/13/2019Подпрограмма для функции ϕ(z) вдоль направления function F1(z: real): real; begin for k:=1 to n do x[k]=x0[k]+z*D[i,k]; F1:=F(x); end; 08/13/2019Подпрограмма для функции ϕ(z) вдоль направления function F1(z: real): real; begin for k:=1 to n do x[k]=x0[k]+z*D[i,k]; F1:=F(x); end;](/img/thumbs/9f5bb4090eaa9f28dbaadfddb3c3f307-800x.jpg)

![Методы нулевого порядка 08/13/2019Подпрограмма преобразования векторов направлений [вычисляет d=∏(d,zm)]Procedure PREOBD; (без параметров) begin . . 08/13/2019Подпрограмма преобразования векторов направлений [вычисляет d=∏(d,zm)]Procedure PREOBD; (без параметров) begin . . . . . D[i.k]=........ end;Отличаются методы видом оператора](/img/thumbs/229930cd5c98393dd8998b0832ed5e08-800x.jpg)
![Методы нулевого порядка 08/13/2019Реализация алгоритма спуска к минимумуBegin D:=0; for i:=1 to n do 08/13/2019Реализация алгоритма спуска к минимумуBegin D:=0; for i:=1 to n do D[i,i]:=1;repeat dl=0;for i:=1 to n do](/img/thumbs/3505d2f44cf90e36e39cba6dcdd63310-800x.jpg)
![Методы нулевого порядка 08/13/2019Преобразование векторов diProcedure PREOBD;Var a:MAS;begin for k=l to n do begin 08/13/2019Преобразование векторов diProcedure PREOBD;Var a:MAS;begin for k=l to n do begin a[k]=0; for i=1 to](/img/thumbs/63ef03bf88fda591edbe94a7be547c8b-800x.jpg)

![Методы нулевого порядка 08/13/2019Procedure PREOBD;//метод РозенброкаVAR a:array[1..n,l..n] of real; c: array[l...,n] of real; aa, cc,ad:real; i,j,k,l: 08/13/2019Procedure PREOBD;//метод РозенброкаVAR a:array[1..n,l..n] of real; c: array[l...,n] of real; aa, cc,ad:real; i,j,k,l: integer;beginfor i=l to n dofor k=l](/img/thumbs/34f1e9436d1f7995c0ef9288bd4f48d1-800x.jpg)