Методы преобразования эпюра

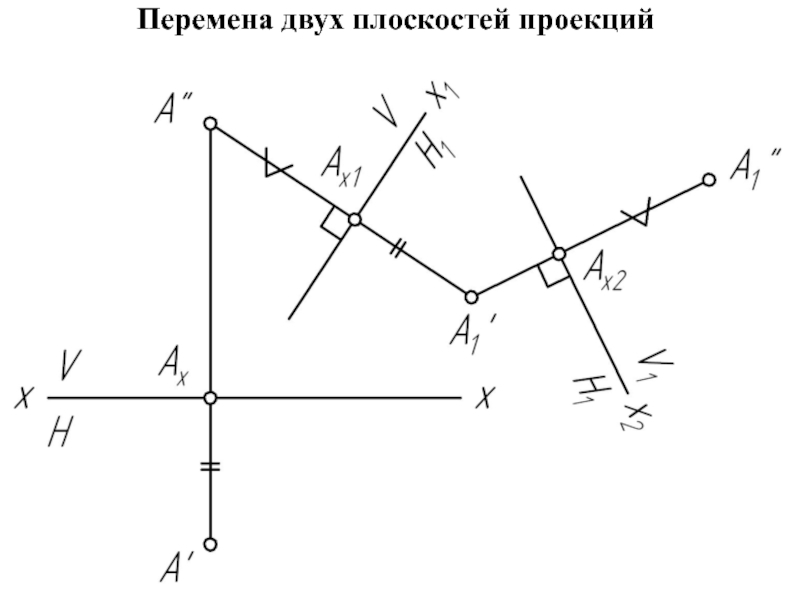
проекции различное положение.

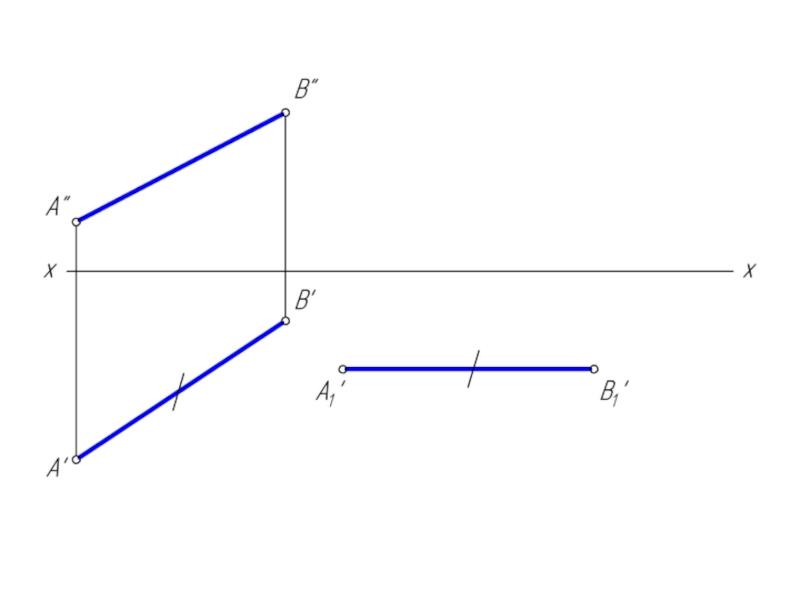
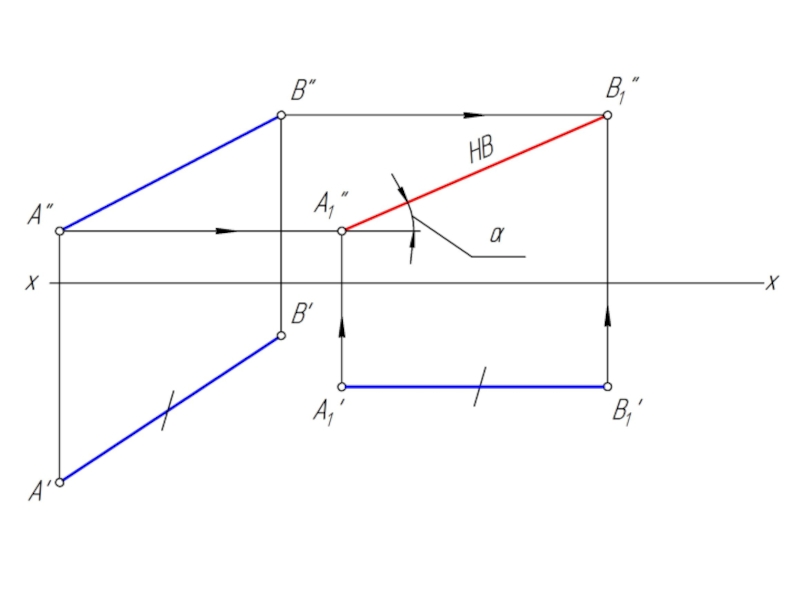
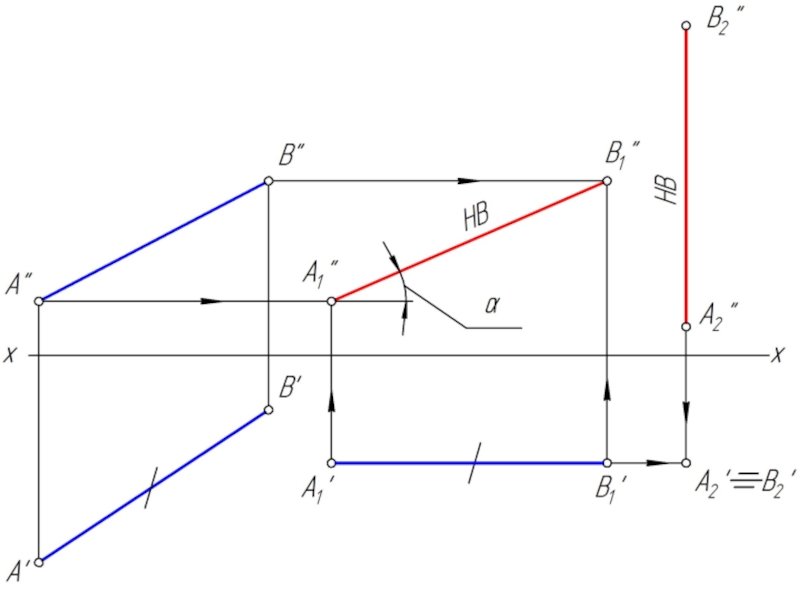
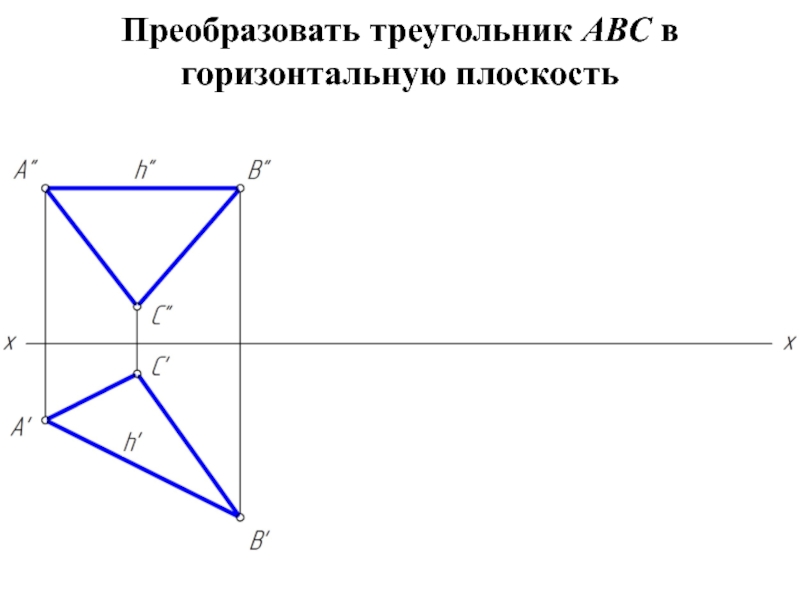
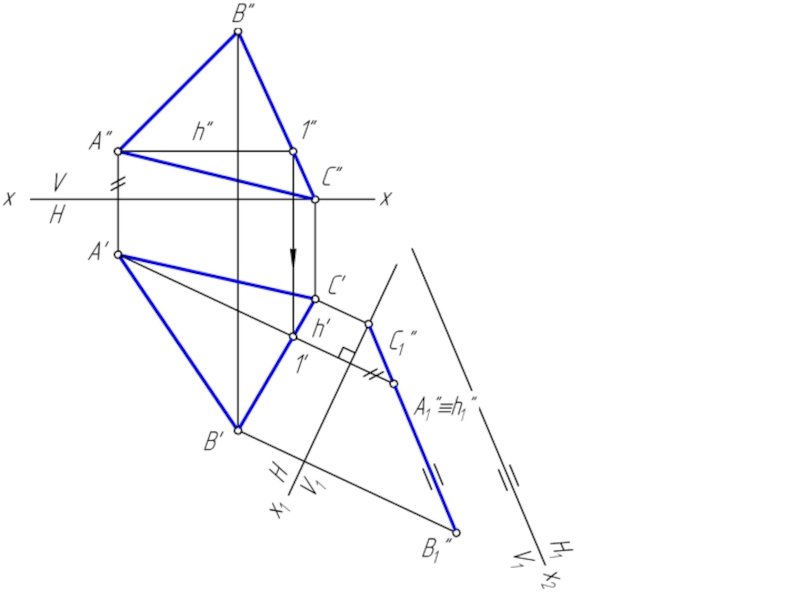
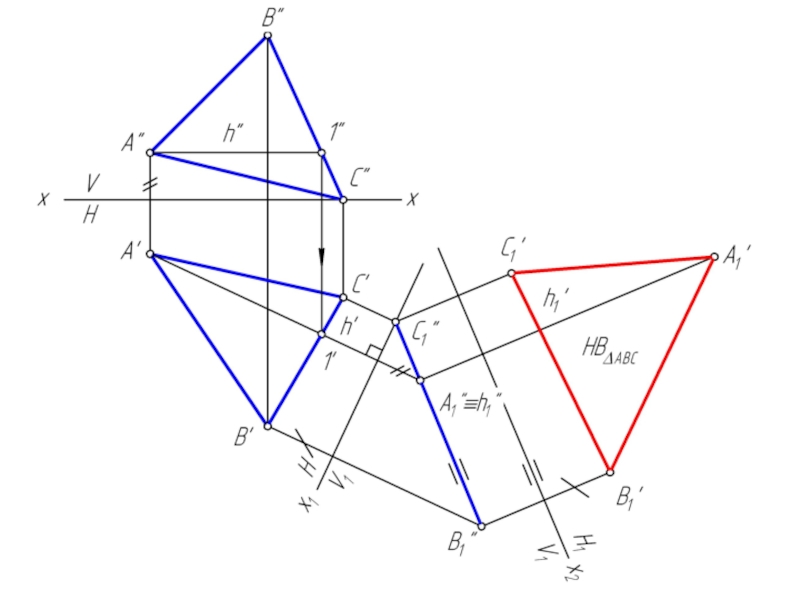
Решение задачи значительно упрощается в случае частного положения

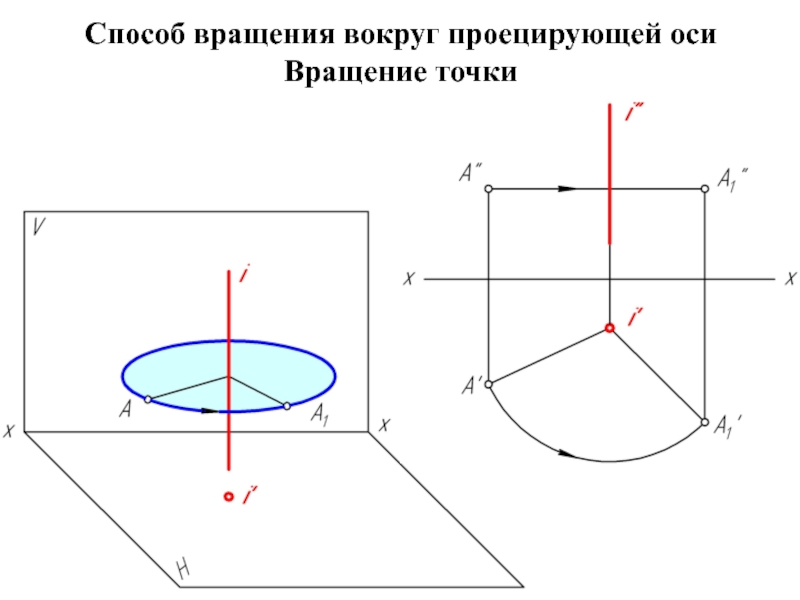
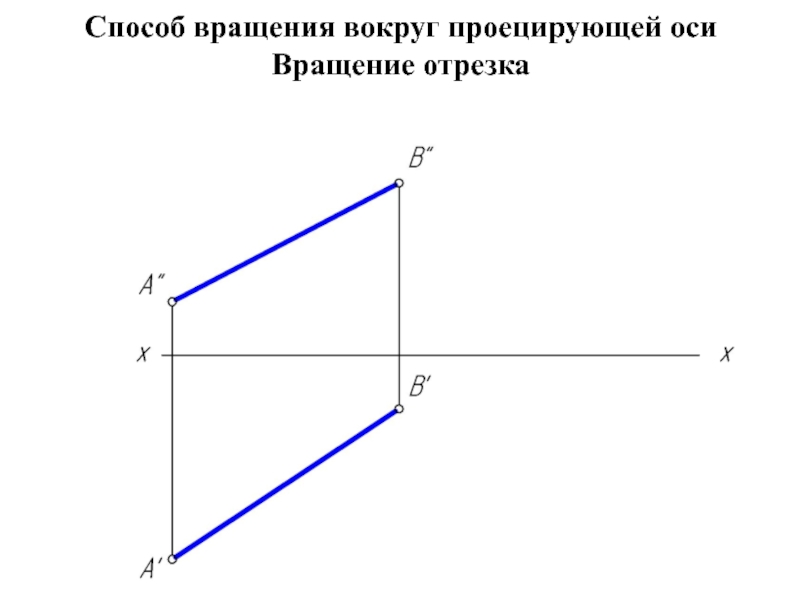
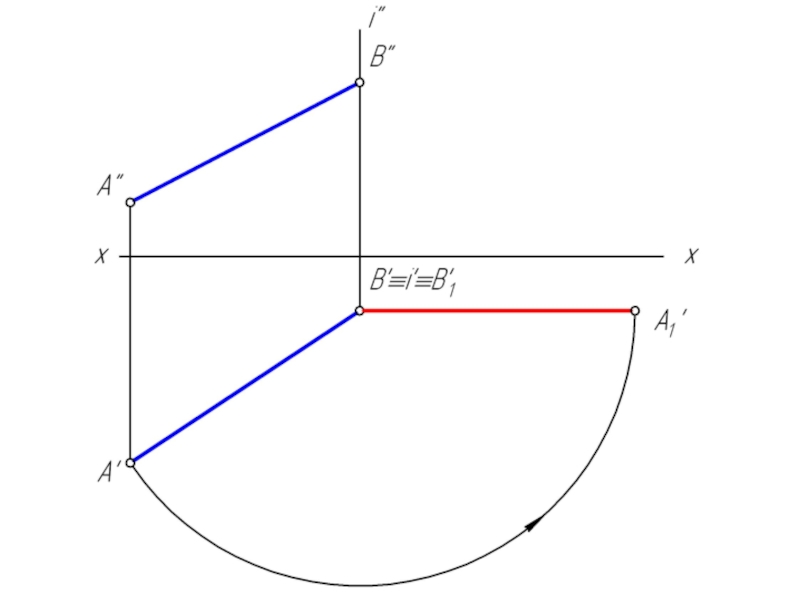
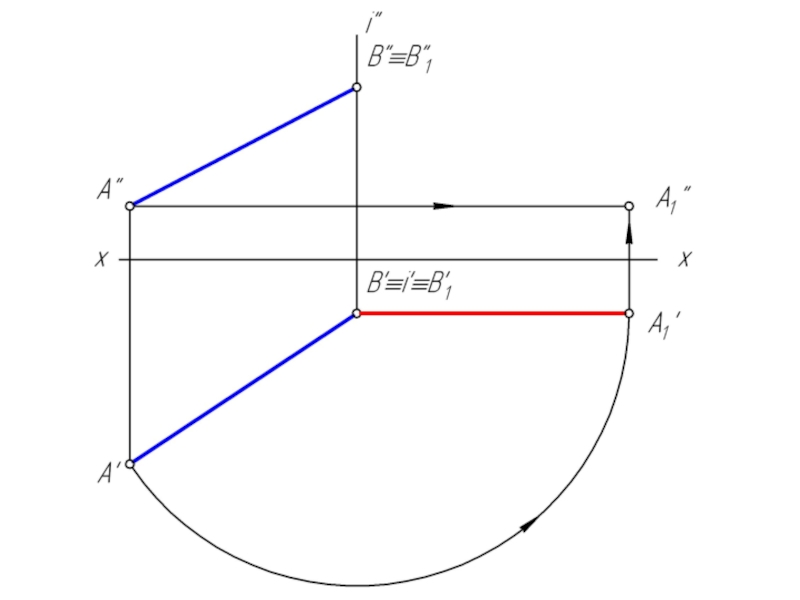
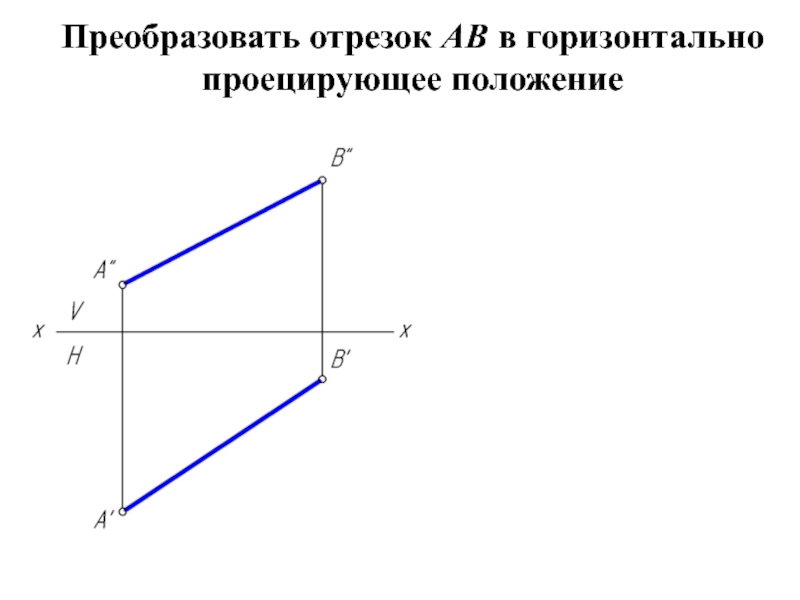
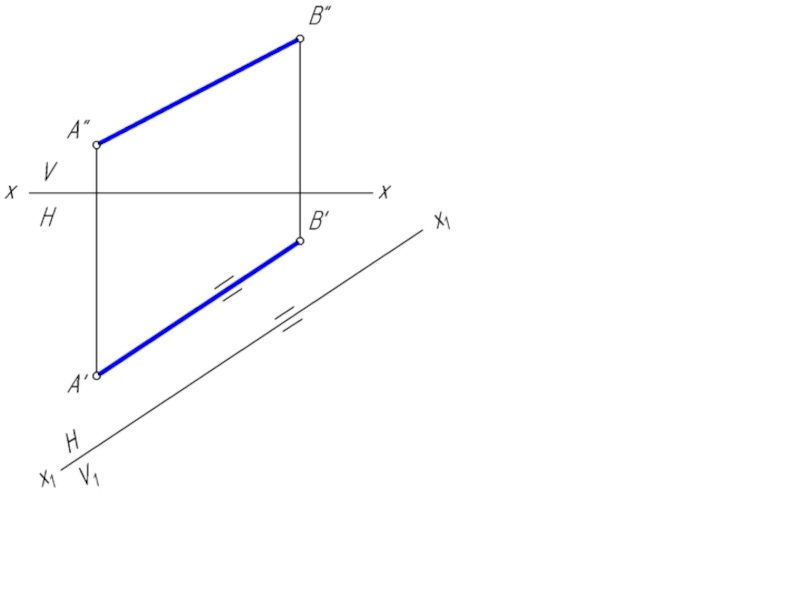
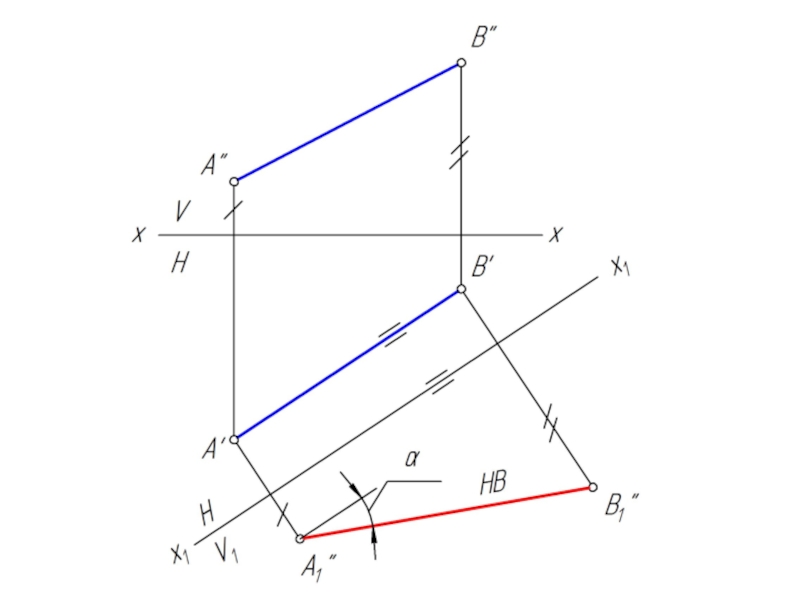
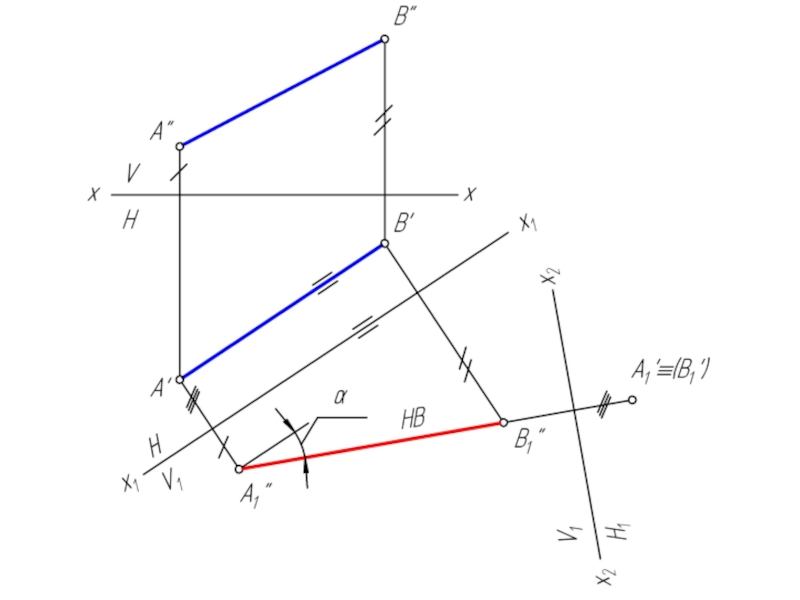
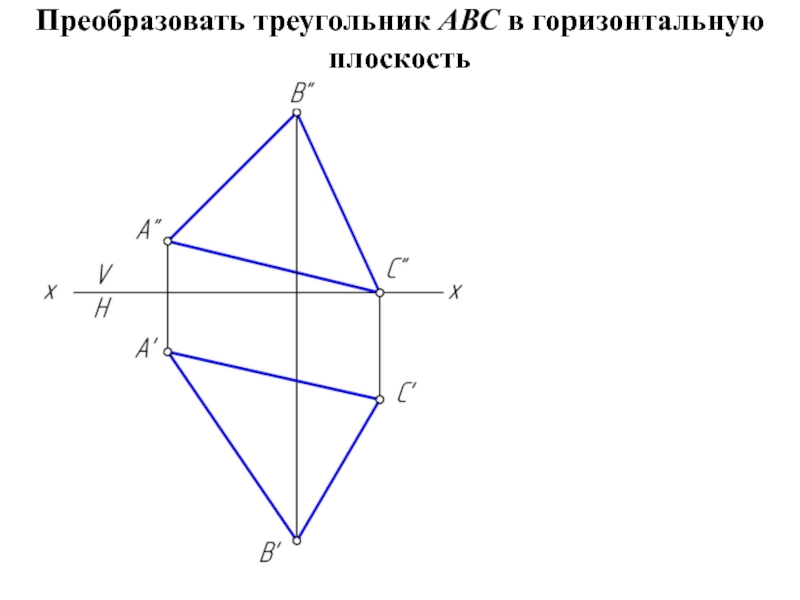
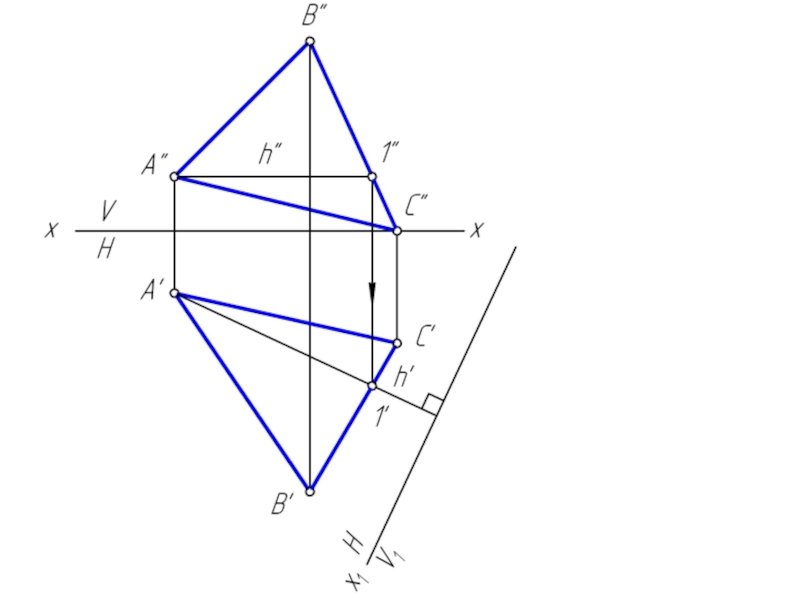
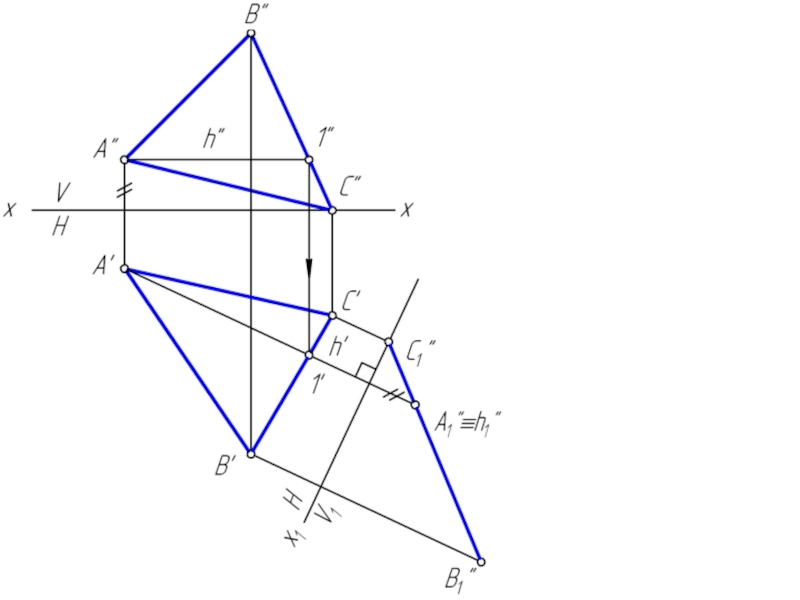
геометрической фигуры относительно плоскости проекции. При этом наиболее выгодным частным положением проецируемой фигуры следует считать:
положение, перпендикулярное к плоскости проекции;
положение, параллельное по отношению к плоскости проекции.

осуществить за счет изменения взаимного положения проецируемой фигуры и плоскости

проекции. При ортогональном проецировании это достигается двумя путями:

1. перемещением в пространстве проецируемой фигуры так, чтобы она заняла частное положение относительно плоскостей проекций, которые при этом не меняют своего положения в пространстве (метод вращения);

2. перемещением плоскостей проекций в новое положение, по отношению к которому проецируемая фигура окажется в частном положении (метод перемены плоскостей проекции).

уровня;
вращение вокруг следа.

Метод перемены плоскостей проекции

фигуры относительно плоскости проекции, проекция фигуры на эту плоскость хотя

и меняет свое положение, но остается конгруентной проекции фигуры в ее исходном положении.
Отметим свойства плоскопараллельного перемещения:

Н, ее фронтальная проекция перемещается по прямой, параллельной оси х;

плоскости, параллельной плоскости проекции V, ее горизонталь-ная проекция перемещается

по прямой, параллельной оси х.

чтобы по отношению к ней проецируемая фигура заняла частное положение,

обеспечивающее получение проекций наиболее удобных для решения поставленной задачи.

Новую плоскость проекции выбирают перпендикулярно к старой. Проецируемые геометрические фигуры при этом не меняют своего положения в пространстве.

оси х1 до новой проекции точки A1" равно расстоянию от

старой оси х до заменяемой проекции A".

расстоянию от старой оси х1 до заменяемой проекции A'.


Перемена двух

плоскостей проекций